图像识别6:综合
图像识别6:综合
- 1实验目的:
-
- 1.实验内容包换:
- 2.实验结果包括:
- 2实验内容:
-
- 一、图像数据的提取
- 二、特征提取
- 三、划分数据集并分类
-
- 3.1决策树
- 3.2 SVM
- 3.3 knn
- 四、可视化
- 五、结果展示
-
- 1. 对resize前后的图像进行展示,包括原始彩图、灰度图、及resize后的灰度图。
- 2. 绘制两个图展示SVM、KNN分类器参数变化时,四种特征提取算法的精度变化。
- 3. 确定最优参数后,使用最优参数下的三个分类器进行分类,展示四种算法在该分类器下的分类精度(五组数据的平均精度)。
- 4. 确定最优参数后,针对分类结果对六类图像的分布进行可视化,三个分类器针对三个图,每个图展示四种算法的可视化结果(取一组数据的分类结果)。
-
- 4.1决策树
- 4.2 KNN
- 4.3 SVM
- 六、源码
1实验目的:
1.实验内容包换:
针对1001 Abnormal Image Dataset数据库,完成图像数据的提取、大小调整,使用留出法按3:2的比例实现五组训练集和测试集的随机划分;
对五组训练集和测试集使用PCA、LPP、LLE、ISOMAP四种算法进行特征提取,并使用SVM分类器、KNN分类器、决策树对特征进行分类;
分类实验包括参数变化分析实验、结果可视化实验。
2.实验结果包括:
1.大小调整前后的图像;
2.分类器参数变化时四种特征提取算法的分类精度变化曲线图;
3.给出最优参数,并给出四种特征提取算法在使用最优参数的分类器下的分类精度;
4.确定最优参数后,针对分类结果对六类图像进行可视化展示;
2实验内容:
一、图像数据的提取
为了提高程序的复用性,在最前面对程序的部分参数进行设置。

通过两层for循环读取指定文件夹路径下的所有图像路径。第一层读取单个文件夹下所有子文件夹信息,包括子文件夹路径sub_path、子文件夹下所有图像名称image_name、子文件夹下图像个数img_num。第二层通过遍历子文件夹下所有图像名称image_name,得到图像路径。最后,根据图像路径读取图像信息。
通过imread读取图像信息为矩阵后,通过rgb2gray函数将有颜色的RGB图像转灰度图像。由于图像大小可能不一致,因此需要使用imresize函数调整为统一大小,本文采用[32,32]格式存储。之后将32*32的数据拉成1行,方便后面数据处理。
最后,由于第一层循环为不同子文件夹下,即对应不同的标签。因此可以根据循环计数的i来给label赋值,1:Aeroplane 2:Boat 3:Car 4:Chair 5:Motorbike 6:Sofa,将与图像信息phi对应的值存在phi_label数组中。

二、特征提取
为了提高算法的健壮性,方便后面代码报错后重跑,设计了一个保存并重新读取的环节。该操作的意义为:将图片数据读取的板块,与后面特征提取等步骤划分开。

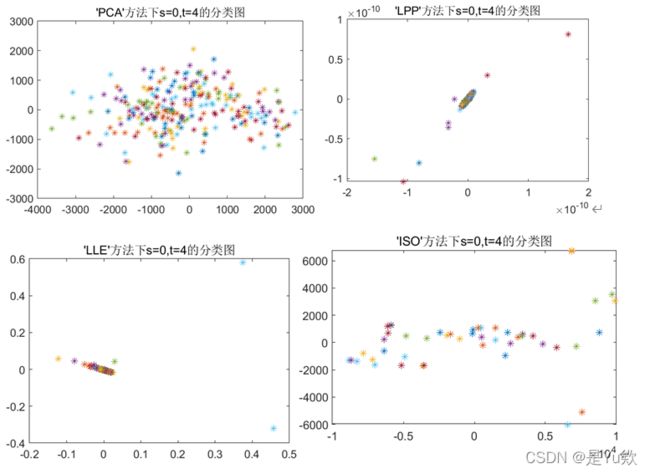
首先设置参数为50,然后使用PCA主成分分析、LPP 局部保留投影、ISOMAP等距特征映射、LLE局部线性嵌入依次对resize数据进行特征提取,目的是降低数据维度,便于计算和可视化,其更深层次的意义在于有效信息的提取综合及无用信息的摈弃。特征提取后,将它们依次保存于dealX{1,1}、dealX{1,2}、dealX{1,3}、dealX{1,4}。
PCA常用于减少数据集的维数,同时保持数据集的对方差贡献最大的特征。

LPP能降低空间维度的同时,较好的保持内部固定的局部结构。其中,LPP函数中存在一个判断条件,由于不满足条件要求会报错并停止继续运行。由于该判断语句无实际影响,因此可以将其注释掉。
ISOMAP采用“局部具有欧式空间性质”的原因,让两点之间的距离近似等于依次多个临近点的连线的长度之和。通过这个方式,将多维空间“展开”到低维空间。
由于部分原有数据分布特征不符合ISOMAP和LLE处理规范,因此处理后的部分数据缺失,因此需要将对应的标签进行更新。这里通过conn_comp找到数据对应的下标,然后读取对应的标签的方式更新dealY。
LLE可以学习任意维的局部线性的低维流形,算法归结为稀疏矩阵特征分解,计算复杂度相对较小,实现容易。但算法所学习的流形只能是不闭合的,且样本集是稠密均匀的。算法对最近邻样本数的选择敏感,不同的最近邻数对最后的降维结果有很大影响。
LLE运算时警告:
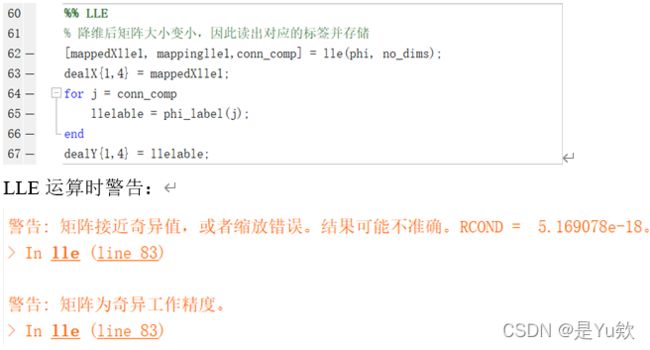
将83行运算符前增加一个点,警告得以解决,但lle提取特征后的数据维度没有变化,说明数据维度变化与此无关。
![]()
查阅资料发现,LLE对数据的流形分布特征有严格的要求。比如不能是闭合流形,不能是稀疏的数据集,不能是分布不均匀的数据集等等,这限制了它的应用。
三、划分数据集并分类
同样,先进行数据存储和读取。

然后,通过for循环读取四种特征提取后的图像数据及对应的标签,然后分别进行五次二划分。
首先通过randperm函数得到一个打乱序列的a,该序列包含(1,n),本文中n为特征提取后矩阵的行数。由于题目要求的3:2划分容易出现不完美分割的情况,因此通过round函数对划分的数量进行取整操作。然后train_num,test_num两个序列分别取打乱序列的3:2,Xtrain,Ytest根据train_num,test_num两个序列的数值取原矩阵对应的列数,最后将按顺序将每次划分结果对应保存于对应的训练集和测试集中,完成随机划分为训练样本Xtrain与测试样本Ytest,同时给出训练样本的标签Xlabel,测试集标签label。

划分完成后,traindata、trainlabel分别为训练集数据集、标签。testdata、testlabel分别为测试集数据集、标签。其中,data的行是样本,列是特征。label的行是样本。

3.1决策树
然后使用决策树进行分类,dt_acc存储四种方法五次二划分结果的精度。

调用函数前,需要看一下函数要求的输入输出大小及参数。
C4_5输入要求:data的行是特征,列是样本。label的列是样本。后两个参数,一个为防止过拟合参数(这里选择5),另一个参数用来确定变量是离散的还是连续的(默认为10)。输出:1行m列,列是测试样本。
绘制决策树分类器随参数变化的精度图。
首先例行存取数据。
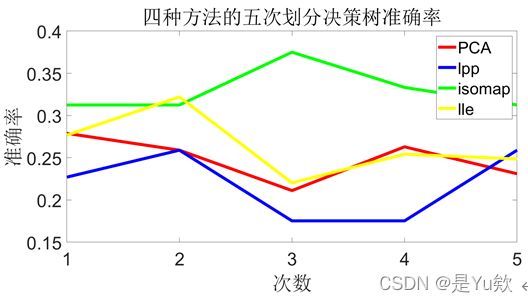
PCA,lpp,isomap,lle的5次决策树准确率分别为0.260558,0.219920,0.333333,0.250847。
3.2 SVM
SVM输入要求:data的行是样本。label的列是样本。
使用SVM进行分类,并探究SVM分类器参数变化下的分类实验,并选取出最优参数、给出最优精度。主要考虑参数‘-s’svm类型和‘-t’损失函数类型对分类精度的影响,对-s和-t参数循环取值为 1到4。
并在最外层循环中,计算不同参数下五次二划分后的准确度均值,将四种数据降维方式的25个参数的数据保存到svm_accs矩阵(4*25)中。

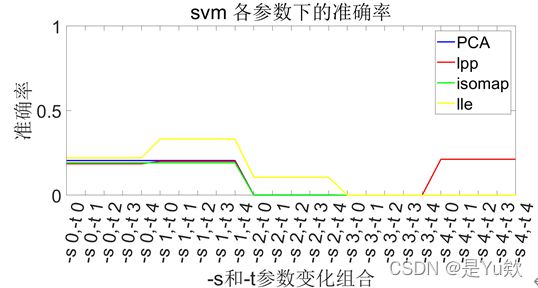
绘制svm分类器各参数下精度变化的图像,方法和决策树类似。
发现各参数变化后精度无变化,一一排查后发现是model的参数有问题。

尝试字符串组合,将原先的["-s “, (s-1)+” -t “, (t-1)]改为[”-s “+num2str(s-1)+” -t "+num2str(t-1)]。

发现-s-t参数对SVM精度影响较大,其中-s类型使用SVM设置类型(默认0 – C-SVC),即分类。核函数的正确选取依赖产生分类问题的实际问题的特点,因为不同的实际问题对相似程度有着不同的度量,核函数可以看作一个特征提取的过程,选择正确的核函数有助于提高分类准确率。
寻找svm的最优参数。

3.3 knn
使用 knn 对其进行分类,参数 k 取 1到25。并计算五次二划分后的准确度均值,将四种数据降维方式25个参数的数据保存到knn_acc矩阵中。

绘制knn分类器各参数下精度变化的图像,方法和决策树类似。

寻找knn的最优参数。

四、可视化
读取和划分与前面基本一致,只需要将no_dims 设置为2,即降维到二维方便可视化,在更改维度后运行并保存数据集。然后直接读取数据集,并进行训练集和测试集的划分。i为数据处理方法,j为全部降维后的测试点,k为测试点的标签(用来给颜色)。

结果可视化。

这里首先取三原色随机数。取随机颜色的代码理论是生成3*6个点,6种不同的颜色每种颜色3个点,但由于’color’,[range,range,range]存在取到相同颜色的情况,因此看不出降维后测试集的标签结果。尝试通过randperm函数强制让他取到不同的颜色。
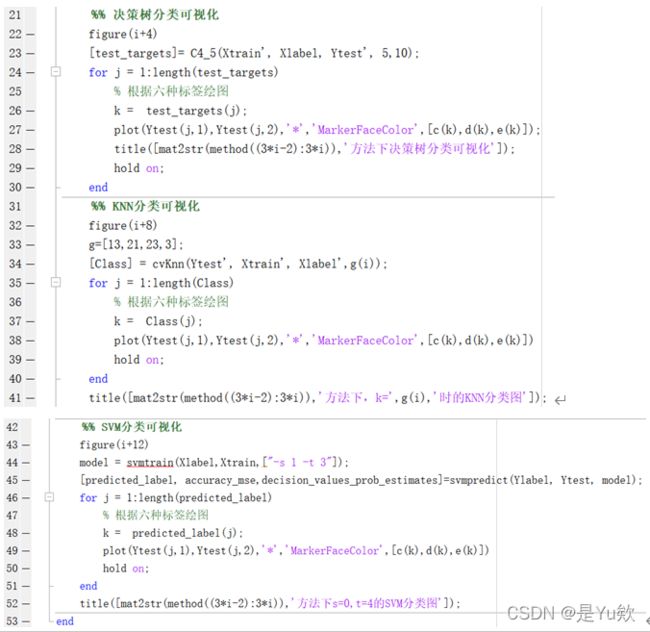
然后进行决策树、KNN、SVM的可视化。首先设置窗口使他们能同时显示,然后给相同标签的点相同的颜色。最后注意title的i,这里的变量较多,较容易混乱。
五、结果展示
1. 对resize前后的图像进行展示,包括原始彩图、灰度图、及resize后的灰度图。
2. 绘制两个图展示SVM、KNN分类器参数变化时,四种特征提取算法的精度变化。
3. 确定最优参数后,使用最优参数下的三个分类器进行分类,展示四种算法在该分类器下的分类精度(五组数据的平均精度)。
PCA LPP ISOMAP LLE
决策树 0.2605 0.2199 0.3333 0.2508
SVM 0.1584 0.1544 0.4128 0.1739
KNN 0.3344 0.1792 0.4298 0.3466
发现SVM分类器精度普遍不高。查阅SVM 怎样能得到好的结果:可以①对数据做归一化(simple scaling)。②样本数>>特征数:如果想使用线性模型,可以使用liblinear,并且使用-s 2参数。③svmtrain只能处理二分类问题,因此当多分类的时候需要改成1v1的,然后再去投票决定。其中③很有道理,寒假可以进一步尝试。
4. 确定最优参数后,针对分类结果对六类图像的分布进行可视化,三个分类器针对三个图,每个图展示四种算法的可视化结果(取一组数据的分类结果)。
4.1决策树
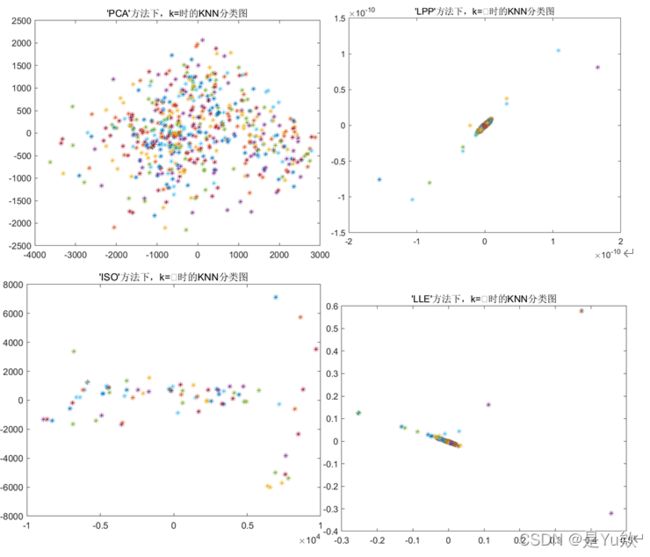
4.2 KNN
4.3 SVM
六、源码
%% resize 1001 Abnormal Image Dataset数据库中的图像
%% 设置参数
clc;clear;close all;
% warning('off') %关掉警告
base_path = 'D:\Desktop\大三上\机器学习\机器学习考查实验\1001 Abnormal Image Dataset';
path = string();
subpath = dir( base_path );
%% 读取指定路径单文件夹下,all文件夹内的all图像
all_imgnum=0;
for i = 1:length(subpath)-2 % 读取单文件夹下,all文件夹% 1,2分别是.和..% 先获取第一个子文件路径,然后获取第二个子文件路径
sub_path = fullfile(base_path, subpath(i+2).name);% disp(sub_path); % D:\Desktop\大三上\机器学习\机器学习考查实验\1001 Abnormal Image Dataset\Aeroplane
image_name = dir(sub_path); % 获取文件夹里的所有图像信息% disp(image_name(3).name); % 1.jpg
img_num=length(image_name)-2; % 文件夹里图像个数% disp(img_num); % 100 114 110 109 85 108
all_imgnum=img_num+all_imgnum;% disp(all_imgnum); % 100 214 324 433 518 626
%% 获取图片数据
for j = 1:img_num % 获取子文件夹下图片的路径
% fullfile函数利用文件各部分信息创建并合成完整文件名
img_path = fullfile(sub_path, image_name(j+2).name); % 子文件夹+图片名称
read_img = imread(img_path); % 读图
if(ndims(read_img)==3)
read_img = rgb2gray(read_img); % RGB图像转灰度图像
end
image = double(imresize(read_img, [32,32])); % 图片统一大小,指定长宽[32,32]
phi(all_imgnum-img_num+j,:)=double(reshape(image,1,[])); % 存放每个图片data于数组phi_cell,一行存放一个图像
end
%% 存放图片label于矩阵phi_label % 定义标签,1:Aeroplane 2:Boat 3:Car 4:Chair 5:Motorbike 6:Sofa
phi_label(1,all_imgnum-img_num+1:all_imgnum)=i*ones(1,img_num);% 行拼接每个标签给对应的图片个数拼成一行
end
%% 保存划分后的数据集
save('Xzong0.mat','phi'); % 存数据
save('Lzong0.mat','phi_label');% 存标签
% 2.使用PCA、LPP、LLE、ISOMAP先对resize后的数据进行特征提取,
% 然后使用SVM分类器、KNN分类器、决策树进行分类。(参考实验8、10、11、12)
% warning('off') %关掉警告
%% 读取数据集
load Xzong0.mat
load Lzong0.mat
%% 设置参数
no_dims = 50; % no_dims设置为50,或者根据特征值数目设置
%% PCA 主成分分析法
[mappedXpca1, mappingpca1] = pca(phi, no_dims);
dealX{1,1} = mappedXpca1;
dealY{1,1} = phi_label;
%% LPP 局部保留投影
% 降低空间维度的同时,能较好的保持内部固定的局部结构,
% 并且它对异化值(通常理解为错误的点,或者为污点)不敏感,与PCA相区别
% [mappedX, mapping] = lpp(X, no_dims, k, sigma, eig_impl)
% 错误使用 lpp (line 24) Number of samples should be higher than number of
% dimensions.样本数量应该大于维度数量。解决:注释掉
[mappedXlpp1, mappinglpp1] = lpp(phi, no_dims);
dealX{1,2} = mappedXlpp1;
dealY{1,2} = phi_label;
%% ISOMAP 等距特征映射
[mappedXisomap1, mappingisomap1,conn_comp1] = isomap(phi, no_dims,5);
dealX{1,3} = mappedXisomap1;
for j = conn_comp1
isomaplable = phi_label(j);
end
dealY{1,3} = isomaplable;
%% LLE 局部线性嵌入
% 降维后矩阵大小变小,因此读出对应的标签并存储
[mappedXlle1, mappinglle1,conn_comp] = lle(phi, no_dims);
dealX{1,4} = mappedXlle1;
for j = conn_comp
llelable = phi_label(j);
end
dealY{1,4} = llelable;
%% 存数据集
save('dealX0zong.mat','dealX'); % 存数据
save('dealY0zong.mat','dealY'); % 存数据
%% 然后使用SVM分类器、KNN分类器、决策树进行分类。(参考实验8、10、11、12)
%% 读取数据集
clc;clear;close all;
load dealX0zong.mat
load dealY0zong.mat
sizei=size(dealX);
for i = 1:sizei(2) % 这个4指的是对于每一个数据处理方法
X = dealX{1,i};
Y = dealY{1,i};
Y = Y' ;
for j = 1:5
fprintf("loading %d %d\n", i, j);
%% 划分数据集
e=round(length(X(:,1))*3/5);
num=randperm(length(X)); %打乱列序列
train_num=num(1:e); %取打乱序列的前60%
test_num=num(e+1:end); %取打乱序列的后40% %end直到数组结尾
% 划分data和label
traindata=X(train_num,:); % 留出法的训练集
trainlabel=Y(train_num,:); % 训练集标签
testdata=X(test_num,:); % 留出法的测试集
testlable=Y(test_num,:); % 测试集标签
%% 实验八的决策树,精度矩阵dt_acc(4*5)
[test_targets]= C4_5(traindata', trainlabel', testdata', 5,10);
temp_count = 0;
for k = 1:length(testlable)
if(testlable(k) == test_targets(k))
temp_count = temp_count + 1;
end
end
dt_acc(i,j) = temp_count/length(testlable);
%% 实验十的svm,精度矩阵svm_acc(5*25),外层循环处理后为4*25
count = 1;
% svm_arg = ["-t 0 -g 0.8","-t 1 -g 0.1","-t 2 -g 3.2","-t 2 -g 6.4","-t 2 -g 12.8"];
% for h = 1:length(svm_arg)
% % 训练不同的参数设置
% model1 = svmtrain(trainlabel',traindata,svm_arg(h));
% [predicted_label, accuracy_mse,decision_values_prob_estimates]=svmpredict(testlable, testdata, model1);
% % 获取不同参数下的分类精度
% svm_acc222(j,count)=accuracy_mse(1)/100;
% count = count + 1;
% end
%% 实验十的svm,精度矩阵svm_acc(5*25),外层循环处理后为4*25
for s = 1:5
for t = 1:5
xticks{count} = sprintf('%s%d%s%s%d','-s ',s-1,',','-t ',t-1); % 将不同的参数设置保存
% 不同的参数设置用来训练
model = svmtrain(trainlabel,traindata,["-s "+num2str(s-1)+" -t "+num2str(t-1)]);
[predicted_label, accuracy_mse,decision_values_prob_estimates]=svmpredict(testlable, testdata, model);
% 获取不同参数下的分类精度
svm_acc(j,count)=accuracy_mse(1)/100;
count = count + 1;
end
end
%% 实验十的knn,精度矩阵knn_acc1(5*25),外层循环处理后为4*25
for k = 1:25
[Class] = cvKnn(testdata', traindata', trainlabel',k);
count = 0;
for n = 1:length(Class)
if(Class(n)==testlable(n))
count = count + 1;
end
end
knn_acc1(j, k) = count / length(testlable);
end
end
for k2 = 1:length(knn_acc1(1,:))
knn_acc(i, k2) = mean(knn_acc1(:,k2));
end
% 在外层循环求svm的精度矩阵svm_acc的平均值(1*25),得到四种方法的五次二划分平均值矩阵(4*25)
for k = 1:length(svm_acc(1,:))
svm_accs(i, k) = mean(svm_acc(:,k));
end
% svm_accs111(1,i) = mean(acc);
% for k = 1:length(svm_acc(1,:))
% svm_accs333(i, k) = mean(svm_acc222(:,k));
% end
end
%% 存数据集
save('dt_acc.mat','dt_acc'); % 存数据
save('svm_acc.mat','svm_acc'); % 存数据
save('knn_acc.mat','knn_acc'); % 存数据
save('svm_accs.mat','svm_accs'); % 存数据
%% 3.选取出最优参数、给出最优精度。(参考实验11、12)
%% 读取数据集
load dt_acc.mat
load svm_acc.mat
load knn_acc.mat
load svm_accs.mat
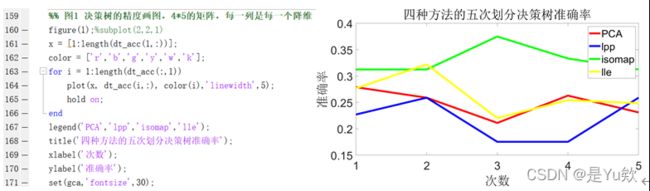
%% 图1 决策树的精度画图,4*5的矩阵,每一列是每一个降维
figure(1);%subplot(2,2,1)
x = [1:length(dt_acc(1,:))];
color = ['r','b','g','y','w','k'];
for i = 1:length(dt_acc(:,1))
plot(x, dt_acc(i,:), color(i),'linewidth',5);
hold on;
end
legend('PCA','lpp','isomap','lle');
title('四种方法的五次划分决策树准确率');
xlabel('次数');
ylabel('准确率');
set(gca,'fontsize',30);
%% 5. 分类精度为5组训练集和测试集上的平均值
fprintf('PCA,lpp,isomap,lle的5次决策树准确率分别为')
for i = 1:length(dt_acc)-1
fprintf('%f,',mean(dt_acc(i,:)))
end
fprintf('svm最佳准确率为')
% disp(svm_accs111);
%% 图2 svm的精度画图,4*25的矩阵,每一列是不同的参数
figure(2);%subplot(2,2,2)
for i = 1:4
x = [1:25];
plot(x,svm_accs(i,:),color(i),'LineWidth',2);
hold on;
end
axis([-inf,inf,0 1]);
xlabel('-s和-t参数变化组合');
ylabel('准确率');
title('svm 各参数下的准确率');
% 设置横坐标
set(gca,'XTickLabel',xticks,'XTickLabelRotation',80,'XTick',[1:1:25],'fontsize',30);
legend('PCA','lpp','isomap','lle');
%% 图3 knn的精度画图,4*25的矩阵,每一列是不同的参数
figure(3);%subplot(2,2,4)
for i = 1:4
x = [1:25];
plot(x,knn_acc(i,:),color(i),'LineWidth',2);
hold on;
end
axis([-inf,inf,0 1]);
xlabel('k参数');
ylabel('准确率');
title('k 调参后的准确率');
% 设置横坐标
set(gca,'XTick',[1:25],'fontsize',30);
legend('PCA','lpp','isomap','lle');
%% 3. 进行SVM、KNN分类器参数变化下的分类实验,并选取出最优参数、给出最优精度。(参考实验11、12)
method = ['PCA', 'LPP','ISO','LLE'];
%% 寻找KNN最优参数
for i = 1:length(knn_acc(:,1))
[m, index] = max(knn_acc(i,:));
fprintf("降维方法 %c%c%c 对应的KNN最优参数:%d ",method((3*i-2):3*i),index);
fprintf("分类精度:%f\n", m);
end
%% 寻找SVM最优参数
for i = 1:length(svm_accs(:,1))
[m, index] = max(svm_accs(i,:));
fprintf("降维方法 %c%c%c 对应的SVM最优参数:%c%c%c%c%c%c%c%c%c",method((3*i-2):3*i),xticks(index));
fprintf("分类精度:%f\n", m);
end
%% 寻找SVM最优参数
for i = 1:length(svm_accs(:,1))
[m, index] = max(svm_accs(i,:));
fprintf("降维方法 %c%c%c 对应的SVM最优参数:-s 21,-t 3",method((3*i-2):3*i));
fprintf("分类精度:%f\n", m);
end
%% 4. 使用最优参数进行分类,对六类图像的分类结果进行可视化。(参考实验7)
load dealX01zong.mat
load dealY01zong.mat
sizei=size(dealX);
for i = 1:sizei(2) % 这个4指的是对于每一个数据处理方法
X = dealX{1,i};
Y = dealY{1,i};
Y = Y';
a = randperm(length(X));
train_num = a( 1,1:round(length(a)*3/5 ) );
test_num = a( 1,round( length(a)*3/5):end );
Xtrain = double(X(train_num,:));
Xlabel = double(Y(train_num,:));
Ytest = double(X(test_num,:));
Ylabel = double(Y(test_num,:));
%% 绘图点的颜色取三原色随机数
c=randperm(1000,6)/1000; % 取6个[0,1]之间不重复的随机数
d=randperm(1000,6)/1000;
e=randperm(1000,6)/1000;
method = ['PCA', 'LPP','ISO','LLE'];
%% 决策树分类可视化
figure(i+4)
[test_targets]= C4_5(Xtrain', Xlabel, Ytest', 5,10);
for j = 1:length(test_targets)
% 根据六种标签绘图
k = test_targets(j);
plot(Ytest(j,1),Ytest(j,2),'*','MarkerFaceColor',[c(k),d(k),e(k)]);
title([mat2str(method((3*i-2):3*i)),'方法下决策树分类可视化']);
hold on;
end
%% KNN分类可视化
figure(i+8)
g=[13,21,23,3];
[Class] = cvKnn(Ytest', Xtrain', Xlabel',g(i));
for j = 1:length(Class)
% 根据六种标签绘图
k = Class(j);
plot(Ytest(j,1),Ytest(j,2),'*','MarkerFaceColor',[c(k),d(k),e(k)])
hold on;
end
title([mat2str(method((3*i-2):3*i)),'方法下,k=',g(i),'时的KNN分类图']);
%% SVM分类可视化
figure(i+12)
model = svmtrain(Xlabel,Xtrain,["-s 1 -t 3"]);
[predicted_label, accuracy_mse,decision_values_prob_estimates]=svmpredict(Ylabel, Ytest, model);
for j = 1:length(predicted_label)
% 根据六种标签绘图
k = predicted_label(j);
plot(Ytest(j,1),Ytest(j,2),'*','MarkerFaceColor',[c(k),d(k),e(k)])
hold on;
end
title([mat2str(method((3*i-2):3*i)),'方法下s=0,t=4的SVM分类图']);
end