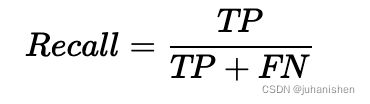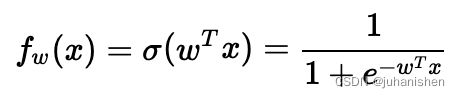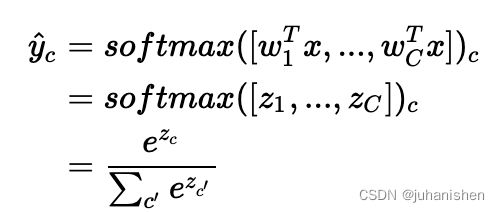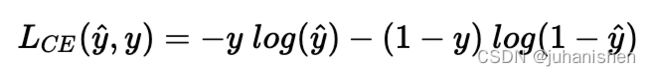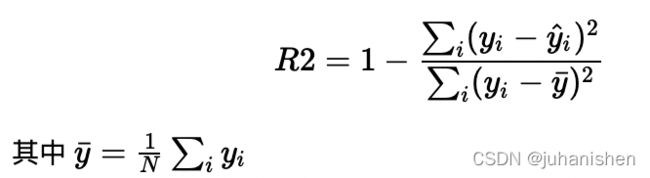机器学习模型评价指标一览
本文有Mcgill大学本科，waterloo大学硕士生林羿在圣一信息技术有限公司实习时，所做的收集。
在这篇文档里，我们会介绍一些常用的机器学习模型评价指标。这些指标会根据模型的目标而分成以下两类：
- 回归模型的指标
- 分类模型的指标
一般来说，这两大类指标是没有重合的，我们要根据不同的模型来选择对应的一个或多个指标。有些指标是模型在学习过程中的优化对象（即损失函数），而有些其他只能用来评判模型的好坏。
1. ~ 分类模型的指标
分类问题可以再细分为 二分类问题（Binary Classification） 以及 多分类问题（Multi-category Classification）。
错误分类损失（Miss-Classification Cost）
这是最基础，最易懂，也是所有分类模型里都能用的一个指标，可以直观的理解为（正则化后的）被错误分类的数据数量比例，仅此而已。他可以作为损失函数进行优化，但同时也有很多缺点：
- 该损失函数不一定连续，无法使用常用的优化器来优化。
- 连续的情况下不一定平滑，也很难优化。
那我们也不是说不能用这个指标。用 1 减去 Miss-Classification Cost 即是模型的准确率，是评判一个模型好坏的最高指标。除此之外，我们来看一些其他的指标。
1.1 ~ 二分类问题的指标
常见的二分类模型有逻辑回归（Logistic Regression）以及支持向量机（Support Vector Machine）。这个章节主要介绍一些常用的二分类问题指标。逻辑回归中用的损失函数交叉熵（Cross Entropy）我们会在下一章节重点介绍。
二分类问题通常用 0 和 1 来代表两种分类的标签。但二分类有个非常特殊的变种：一类问题。一类问题可以被简单理解成“是或不是”，通常用 -1 和 1 来表示他的标签。我们把这两种类型的指标放在一起讲。
首先最基础的衡量标准就是真正例（True Positive）和假正例（False Positive）：
- 真正例TP： 正类数据中被正确分类的数据，即 1 被正确预测，预测值为 1
- 真负例TN： 负类数据中被正确分类的数据，即 0（-1）被正确预测，预测值为 0（-1）
- 假正例FP： 负类数据中被错误分类的数据，即 0（-1）被错误预测，预测值为 1
- 假负例FN： 正类数据中被错误分类的数据，即 1 被错误预测，预测值为 0（-1）
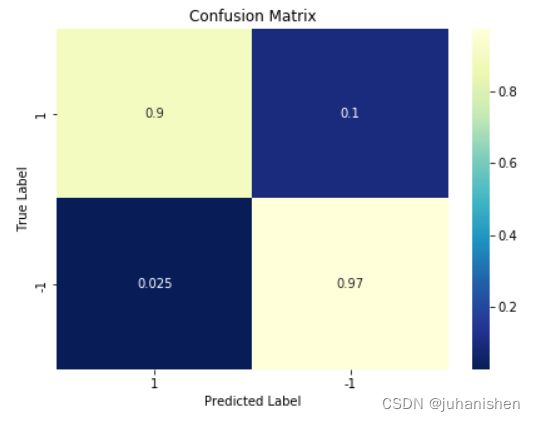
基于这四个值，我们可以生成 混淆矩阵（Confusion Matrix） 方便我们我们浏览这些数字。以下是一个一类问题中用到混淆矩阵：
新奇检测和异常检测是一类问题的两个常见场景。在这类场景中，我们首先最关心的就是不能有太高的假正例 FP。想象一个癌症病人被判定为没有癌症是非常可怕的。所以 FP 值便是我们判断一个一类模型的标准。
除此之外，我们还可以从上面的这四个基础数值得到很多别的指标：
- Precision： 被模型分类为Positive（标签为1）的数据中，有多少真的是Positive的 ？
- Recall： 实际应该是Positive的数据中，有多少被我们选为了Positive？
但Precision和Recall都不能很完美的去评判一个模型的好坏，他们都只看到了其中一面。而F1 Score是个更好的标准：
- F1 Score： 最最泛用的KPI，结合了Precision和Recall，公式为：
可以看出 F1 Score 其实是 Precision 和 Recall 的调和平均数。最大值是1， 最小值是0。F1值越大说明模型在判断正类数据上越成功。但仍然需要结合假正例来判断模型在对负类数据上的效率。
注意：以上这些指标均不能作为损失函数进行优化
ROC 图像 和 AUC
roc曲线：接收者操作特征 (receiveroperating characteristic), roc曲线上每个点反映着对同一信号刺激的感受性。
该图像的横轴是False Positive Rate （FPR），纵轴是True Positive Rate (TPR)。计算方式分别为 FPR = FP /（FP + TN）， TPR = TP /（TP + FN）。ROC 的具体定义如下：
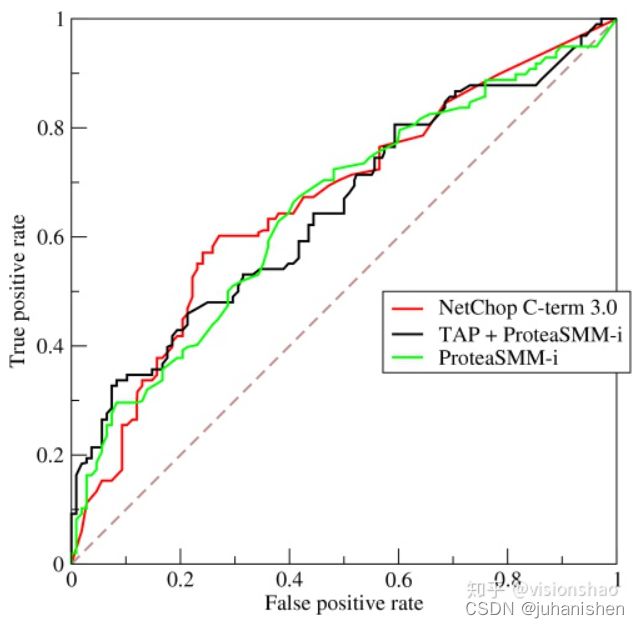
对于样本数据，我们使用分类器对其进行分类，分类器会给出每个数据为正例的概率，我们可以针对此来设定一个阈值，当某个sample被判断为正例的概率大于这个阈值时，认为该sample为正例，小于则为负例，然后通过计算我们就可以得到一个(TPR , FPR)对，即图像上的一个点，我们通过不断调整这个阈值，就得到若干个点，从而画出一条曲线。一个真实的ROC图像例子如下
我们可以看出，当这个阈值越大时，越多的样本被分为负例，TPR下降（正例数据被分为负例了），FPR下降（负类数据更不会被分为正例，但是影响要比TPR小，所以斜率呈上升趋势）。阈值越小时，越多的样本被分为正例，这样一来TPR上升（更多的正例样本被分为正例），FPR上升（更多的负例样本被分为正例，影响更大，所以斜率呈下降趋势）。
AUC (Area under Curve)：Roc曲线下的面积，介于0.5和1之间。Auc作为数值可以直观的评价分类器的好坏，值越大越好。 AUC是可以作为损失函数进行优化的，具体步骤就不在这里介绍了。
1.2 ~ 多分类问题的指标
我们常见的多分类（Multi-Class Classification）机器学习模型有：决策树 / 决策森林（Decision）、softmax回归（softmax regression）。针对多分类问题（还有刚才的逻辑回归），我们重点介绍熵（Entropy）和交叉熵（Cross Entropy）。
在开始之前，我要先来讲讲逻辑回归和SoftMax回归的定义，因为交叉熵在两种模型里的定义有些区别。
1.2.1 ~ 逻辑回归和Softmax回归
逻辑回归（Logistic Regression） 是线性回归的变种，是一个二分类模型。如果我们的数据集是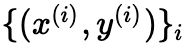 
，且 
是个二分类数据集，则逻辑回归模型学习一个权重参数
，且预测函数为
- 输出为 [0,1][0,1] 的一个 "概率分布"（不是真正的概率分布）
- 需要有个阈值（e.g. 0.5）来最后判断 xx 属于 0 还是 1。
Softmax回归 就是逻辑回归的多类别版本。还是上面那组数据集，但 y^{(i)} = \{1, ..., C\}y(i)={1,...,C}。这个模型中我们的学习对象是一组
wc∈Rd,c∈{1,...,C}。用Softmax函数计算 
，被分类到 cc 的 “概率”：
同样，对于每个类别 
就是预测得到的 “概率分布”。
说完这两种模型，我们就可以开始正式介绍交叉熵的概念了。
1.2.2 ~ 熵、交叉熵
熵（Entropy） 又称信息熵，用来描述整个随机分布所带来的信息量期望值。如果 y 是随机变量，C 代表分类的数量，则熵 H(y)的定义如下
从上式可以看出：
- -log p(y=c) 是观测到 c 时的信息量。
- 熵只依赖于随机变量的分布,与随机变量取值无关；
- 对于某一个类别c来说，如果 p(y=c) = 1 则H(y) = 0，此时没有任何信息，所有事情都是确定的。
- 当概率越小时，混乱程度越大，信息熵也越大。所以熵代表了随机分布的混乱程度。
交叉熵（Cross Entropy），又称负对数似然（Negative-log Likelihood），其广泛用在逻辑回归的Sigmoid和softmax函数中作为损失函数使用。作用是度量两个概率分布间的差异性信息。
交叉熵在逻辑回归和Softmax回归中的表达式不太一样。
对于单组预测值 
和 真实值 y来说，他们之间的交叉熵定义为
从上式我们可以注意到：
- 这是一个连续平滑的函数，一阶导数连续，所以可以优化
- 如果
是通过
得出的，则 L是一个 w 的凸函数，根据优化理论，至多拥有一个最小值。是优化理论非常喜欢的一个函数类型。 - 良好的概率解释
我们来看一下在逻辑回归和Softmax回归模型下的交叉熵表达式：
逻辑回归交叉熵损失函数
这个式子只是把
带入了，并求了个和。
Softmax回归交叉熵损失函数
这种情况稍微复杂一些，要把前文的 y 值都进行one-hot encoding，从标量变成一个
矢量（C是类别数量），且元素只有0 和 1。以下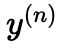 
均代表矢量。
2. 回归模型的指标
回归模型本质就是拟合一个函数。和分类模型不同，回归模型预测是一个具体的数值，而不是一个分类了。所以回归模型的指标都是用不同的方法来计算预测的数值和真是数值的误差，因此这些指标都比较泛用。接下来就来介绍几个常用的指标。
- 连续不平滑，故一阶导数不连续（不平滑的点不存在导数），不好优化
- 但仍然简单直观，方便理解，可以是判断指标，不太会作为损失函数优化
MSE（Mean Squared Error） 均方误差 和 RMSE（Root Mean Squared Error） 均方根误差
MSE又称 L2 Loss 比较常用。
R2决定系数
R2的取值范围是 [0,1]
- R2 是多元回归中的回归平方和占总平方和的比例，它是度量多元回归方程中拟合程度的一个统计量，反映了在因变量y的变差中被估计的回归方程所解释的比例。
- R2 越接近1，表明回归平方和占总平方和的比例越大，回归线与各观测点越接近，用x的变化来解释y值变差的部分就越多，回归的拟合程度就越好。
Reference
- Understanding AUC - ROC Curve