初阶数据结构——线性表——链表——带头双向循环链表

想快速入门数据结构，推荐订阅作者的初阶数据结构专栏！此专栏预计更新：顺序表，链表，栈，队列，二叉树，排序算法等等

初阶数据结构我们通过c语言实现，所以此专栏也可以帮助大家巩固大家的c语言知识

源代码已上传至我的码云

博主的微信公众号关注啦，关注我每天学习一道题，点我关注

前言

其中在链表的实现中有很多种实现方法，主要取决于以下几个因素

单向还是双向？
循环还是不循环？
带头还是不带头

这几个特征两两组合，就可以看做一种链表的实现方式

但在实际中运用最大的，其中就只有以下两种：

不带头单向不循环和我们本文的实现方式——双向带头循环

其中前者在oj题中考的特别多，而且可以作为其它数据结构，比如哈希桶的子结构，所以应用比较广泛

但是，前者却不适合用来存储数据

因为我们在尾插，尾删等函数接口中，需要遍历查找链表尾

而且，还需要考虑头结点为空等等问题

所以，我们引入了带头双向循环链表，带头结点可以有效解决插入时链表为空的问题，而循环可以解决寻找尾结点的问题，双向让我们方便寻找当前结点的前面一个结点

在本文中实现的结构虽然看起来复杂，但是实现却非常简单，在实际应用中也最适合于存储数据

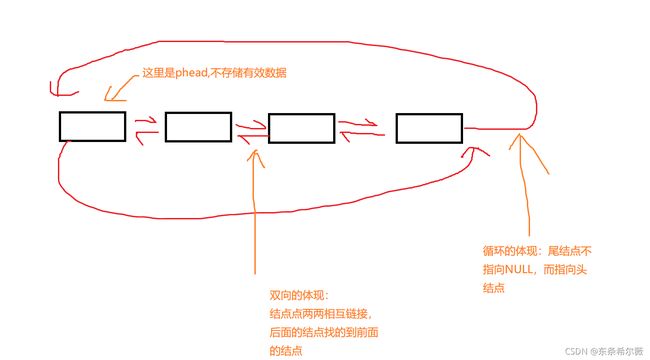
其中循环的体现：尾结点不指向NULL，而指向头结点

双向的体现：结点间两两相互链接，后面结点可以找到前面的结点

逻辑结构图如下

双向链表定义

与单链表差不多用结构体定义，不过需要多一个prev指针存储前面结点的地址

定义

typedef struct ListNode
{
	LTDataType data;
	struct ListNode* next;
	struct ListNode* prev;
}LTNode;

同样，为了方便存储类型的替换，将我们的数据类型统一命名

typedef int LTDataType;

初始化

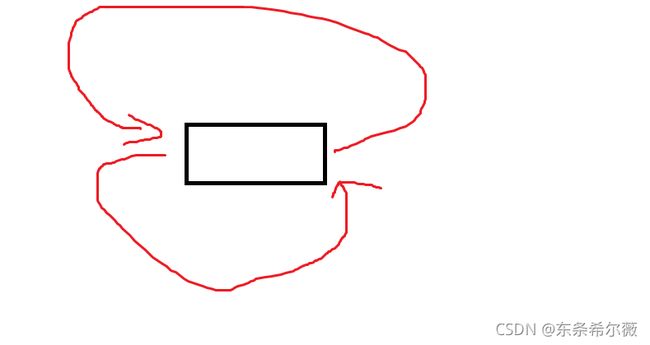
因为我们的链表是带头的，所以我们在初始化的时候需要开辟一个头结点出来
头结点的特征：**不存储有效数据，**所以我们初始化的时候不需要初始化头结点中的数据

我们为了满足循环的特征，将头结点的next和prev都指向自己

LTNode* ListInit()
{
	LTNode* head = malloc(sizeof(LTNode));
	if (!head)
	{
		printf("malloc fail\n");
		exit(-1);
	}
	head->next = head;
	head->prev = head;
	return head;
}

初始化函数使用：

LTNode* plist = ListInit();

双向链表的插入

在本文插入中，传参不再用到二级指针，因为头指针的指向永远不会改变

并且，无需考虑边界情况

插入函数

前文中已经介绍，这里不再详细阐述

LTNode* BuyListNode(LTDataType x)
{
	LTNode* newnode = malloc(sizeof(LTNode));
	if (!newnode)
	{
		printf("malloc fail\n");
		exit(-1);
	}
	newnode->data = x;
	newnode->prev = NULL;
	newnode->next = NULL;
	return newnode;
}

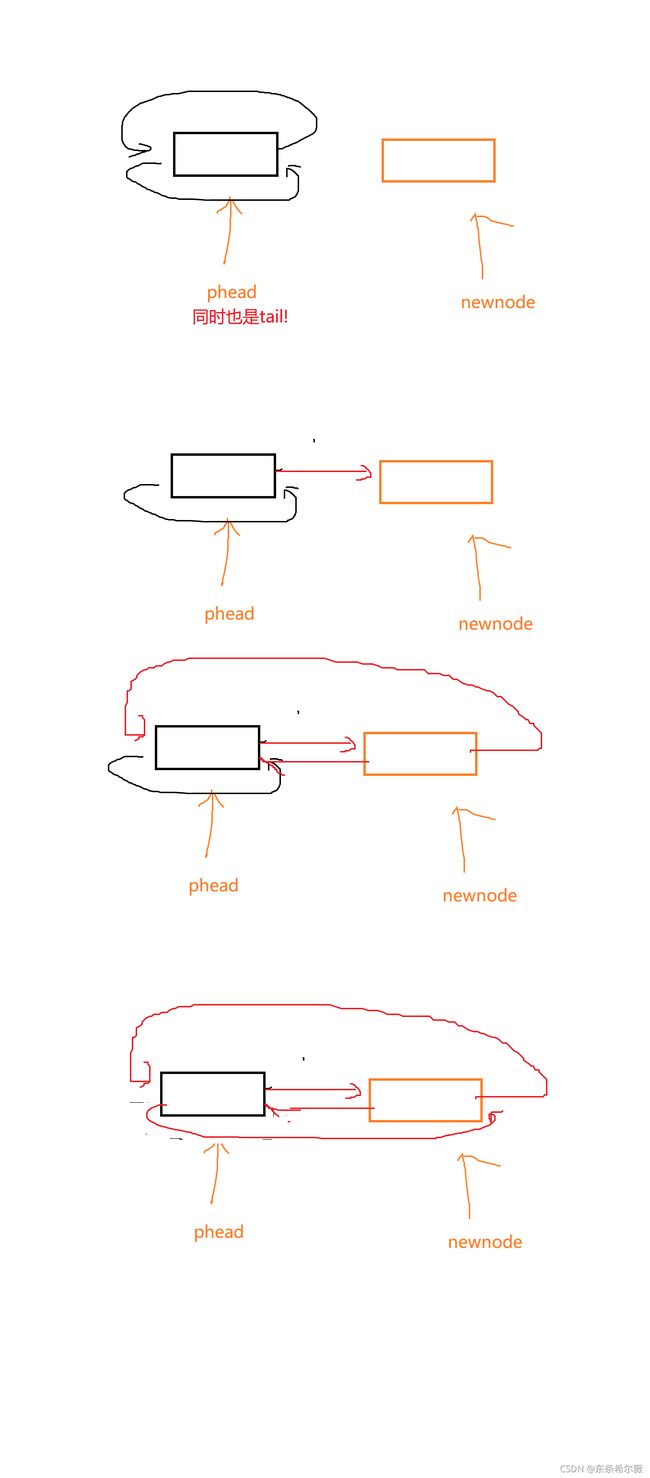
尾插

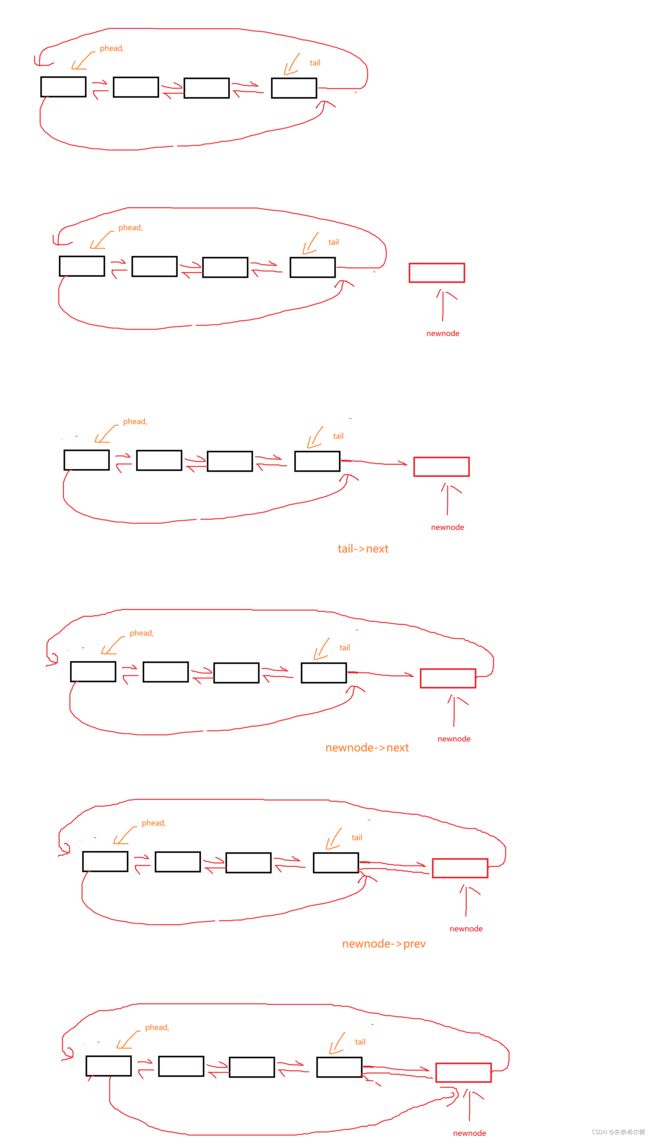
有了尾结点，我们的尾插就变的相对简单的多

根据循环的特征，我们头结点的前面一个结点就是尾结点

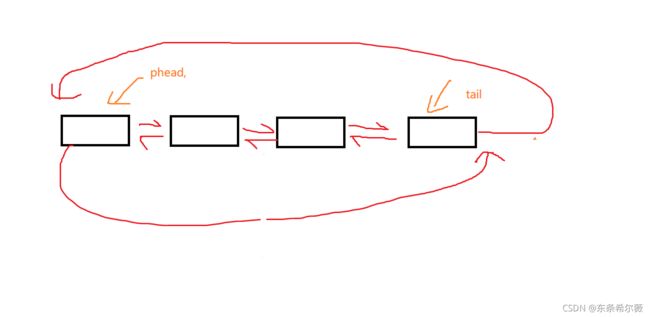
我们开辟出一个新结点后，与单链表不同的是，需要注意有tail->next,newnode->prev，还有最重要的newnode->next=phead,phead->prev=newnode

void ListPushBack(LTNode* phead, LTDataType x)
{
	assert(phead);
	LTNode* newnode = BuyListNode(x);
	LTNode* tail = phead->prev;

	tail->next = newnode;
	newnode->prev = tail;
	newnode->next = phead;
	phead->prev = newnode;
}

对边界情况的讨论：

空链表

所以，在后续的插入中，我们并不需要特殊讨论

头插

头插在头结点后面插入就行了，这里不再详细阐述

要注意它们之间的相互链接关系：

newnode和phead和原来的phead->next都需要做到两两相互链接

这里的phead->next如果看的不顺眼，也可以用变量代替

void ListPushFront(LTNode* phead, LTDataType x)
{
	assert(phead);

	LTNode* newnode = BuyListNode(x);

	newnode->next = phead->next;
	newnode->prev = phead;
	phead->next->prev = newnode;
	phead->next = newnode;
}

任意位置插入

同样，我们需要查找函数来查找我们需要插入的位置，参数传递也只需要传入这个位置的指针

因为我们现在方便查找前面的结点，所以我们可以实现在pos位置之前的插入

为了方便，用posPrev记录pos位置之前的结点

注意链接关系就行，没什么难度

边界情况为空链表，头插，尾插，大家可以尝试走读代码，可以发现边界情况在这种结构中通通不用考虑

void ListInsert(LTNode* pos, LTDataType x)
{
	assert(pos);

	LTNode* newnode = BuyListNode(x);
	LTNode* prevPos = pos->prev;
	prevPos->next = newnode;
	newnode->next = pos;
	pos->prev = newnode;
	newnode->prev = prevPos;
}

双向链表的删除

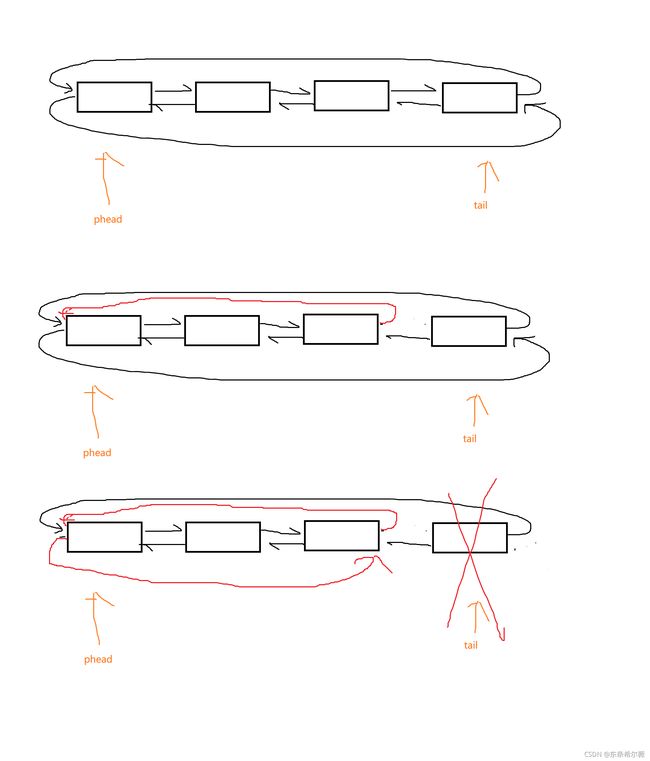
尾删

我们同样方便找到尾部的结点

需要变量来记录，重新建立链接关系时，绕开尾结点即可

最后把尾结点释放掉

但是，这里的边界情况需要讨论

当链表为空时，我们再调用这个函数的话，连头结点也会被释放掉

所以为了避免这个问题，我们可以加一个断言，判断phead->next是不是它本身即可

void ListPopBack(LTNode* phead)
{
	assert(phead && phead->next != phead);

	LTNode* tail = phead->prev;
	tail->prev->next = phead;
	phead->prev = tail->prev;
	free(tail);
	tail = NULL;

}

头删

同样绕开头结点即可，没什么难度

void ListPopFront(LTNode* phead)
{
	assert(phead && phead->next != phead);
	LTNode* head = phead->next;

	head->next->prev = phead;
	phead->next = head->next;

	free(head);

	head = NULL;
}

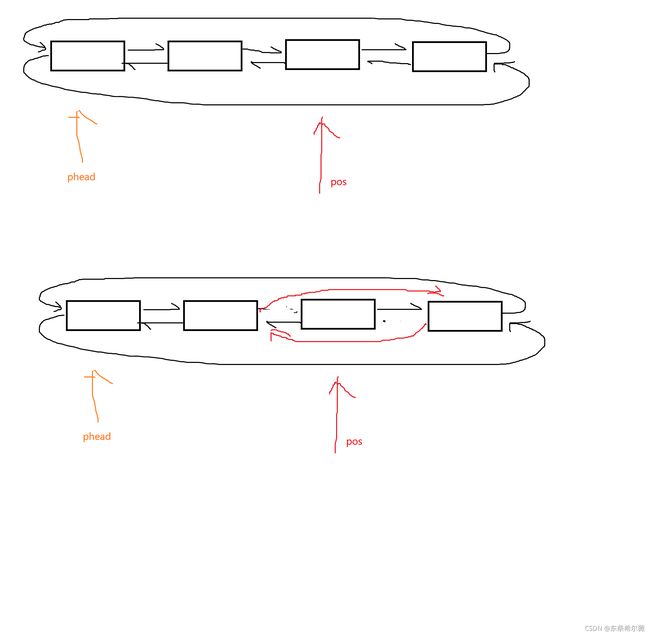
任意位置的删除

任意位置删除只需要修改两个结点就可以绕开我们当前需要释放的结点

void ListErase(LTNode* pos)
{
	assert(pos);

	pos->prev->next = pos->next;
	pos->next->prev = pos->prev;
	free(pos);
	pos = NULL;
}

查找函数

使用方法已经在前文介绍过了，这里不再做过多的阐述

但是这里我们的查找是从头结点的下一个结点开始的，结束条件是看是不是遍历回到了头结点，因为这是循环链表，如果条件设置不恰当，很容易造成死循环

LTNode* ListFind(LTNode* phead,LTDataType x)
{
	assert(phead);

	LTNode* cur = phead->next;
	while (cur != phead)
	{
		if (cur->data == x)
			return cur;
		cur = cur->next;
	}
	return NULL;
}

但我们可以发现，在链表中最优的结构中，查找的时间复杂度仍然是O(N)，所以查找复杂度高是链表中最大的缺点

打印函数

同样是遍历打印

void ListPrint(LTNode* phead)
{
	assert(phead);

	LTNode* cur = phead->next;
	while (cur != phead)
	{
		printf("%d<->", cur->data);
		cur = cur->next;
	}
	printf("end\n");
}

链表销毁

为了防止内存泄露，在我们使用完链表后，最好将它们全部销毁

在这里我们最后才释放phead，因为phead是我们的判断条件

为了防止当前位置释放后找不到下一个结点，我们在这里用两个指针来遍历

void ListDestory(LTNode* phead)
{
	assert(phead);

	LTNode* cur = phead->next;
	LTNode* next = cur->next;
	while (cur != phead)
	{
		free(cur);
		cur = next;
		if(next != phead)
			next = cur->next;
	}
	free(phead);
	phead = NULL;
}

一个使用示例

void LTest3()
{
	LTNode* plist = ListInit();//初始化链表

	ListPushBack(plist, 1);
	ListPushBack(plist, 2);
	ListPushBack(plist, 3);
	ListPushBack(plist, 4);
	ListPushBack(plist, 5);//尾插一些数据
	ListPrint(plist);//打印函数

	LTNode* pos = ListFind(plist, 2);//查找某个数字的位置，并返回
	LTNode* pos2 = ListFind(plist, 4);
	ListInsert(pos, 6);//利用find找到的位置来插入
	ListPrint(plist);
	ListErase(pos2);
	ListPrint(plist);
	ListDestory(plist);//使用完要销毁链表
}

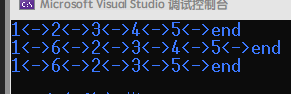
运行截图：