恭喜你~遇到了最有趣的排序算法

哈喽~大家好鸭，看到这标题是不是很是疑惑？是不是在想，唉？排序算法…… 额，算法还能叫有趣，别扯了吧。哈哈哈，看了这篇你就知道啥叫 “有趣” 的排序。

 个人主页：个人主页​​​​​

 系列专栏：【算法】​​​​​​

与这篇算法相关的文章：

操作系统中几种最最最常见的调度算法	操作系统中几种最最最常见的调度算法（适用于软件设计师考试与期末考试复习）_一个名叫追的程序猿的博客-CSDN博客
用 JSP 连接 MySQL 登入注册项目实践	用 JSP 连接 MySQL 登入注册项目实践(JSP + HTML + CSS + MySQL)_一个名叫追的程序猿的博客-CSDN博客
软件测试来喽~这看这博主写的多是一件美事呀	软件测试来喽~这看这博主写的多是一件美事呀_一个名叫追的程序猿的博客-CSDN博客

目录

开篇介绍

首先啥是排序？

​一、插入排序

1、直接插入排序

2、希尔排序

二、选择排序

1、简单选择排序

2、堆排序

三、交换排序

1、冒泡排序

2、快速排序

四、归并排序

五、基数排序

总结 

---

开篇介绍

首先啥是排序？

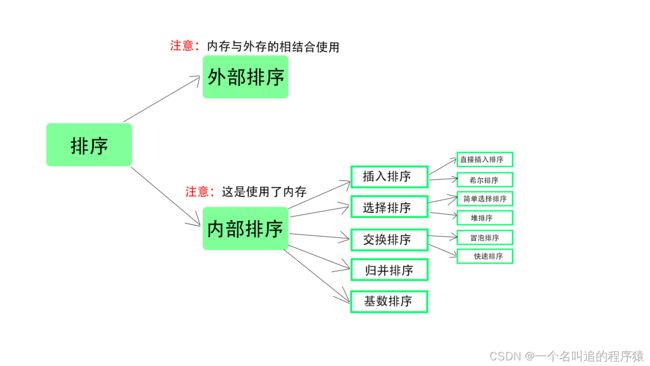
排序是计算机内经常进行的一种操作，其目的是将一组“无序”的记录序列调整为“有序”的记录序列。分内部排序和外部排序，若整个排序过程不需要访问外存便能完成，则称此类排序问题为内部排序。反之，若参加排序的记录数量很大，整个序列的排序过程不可能在内存中完成，则称此类排序问题为外部排序。内部排序的过程是一个逐步扩大记录的有序序列长度的过程。

上面的话可以理解为排序可以分为外部排序（内存与外存的相结合使用）和内部排序（使用了内存）。

内部排序分为：插入排序（直接插入排序和希尔排序）、选择排序（简单选择排序和堆排序）、交换排序（冒泡排序和快速排序）、归并排序、基数排序，如下图所示。那么下面我们来看看吧。

​一、插入排序

1、直接插入排序

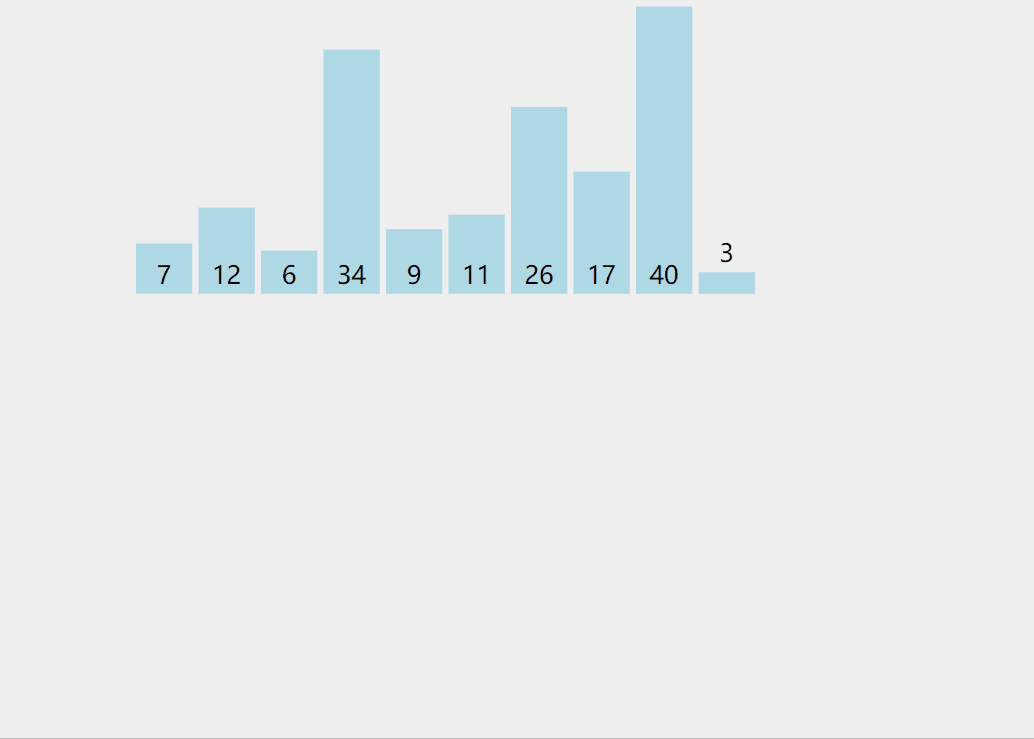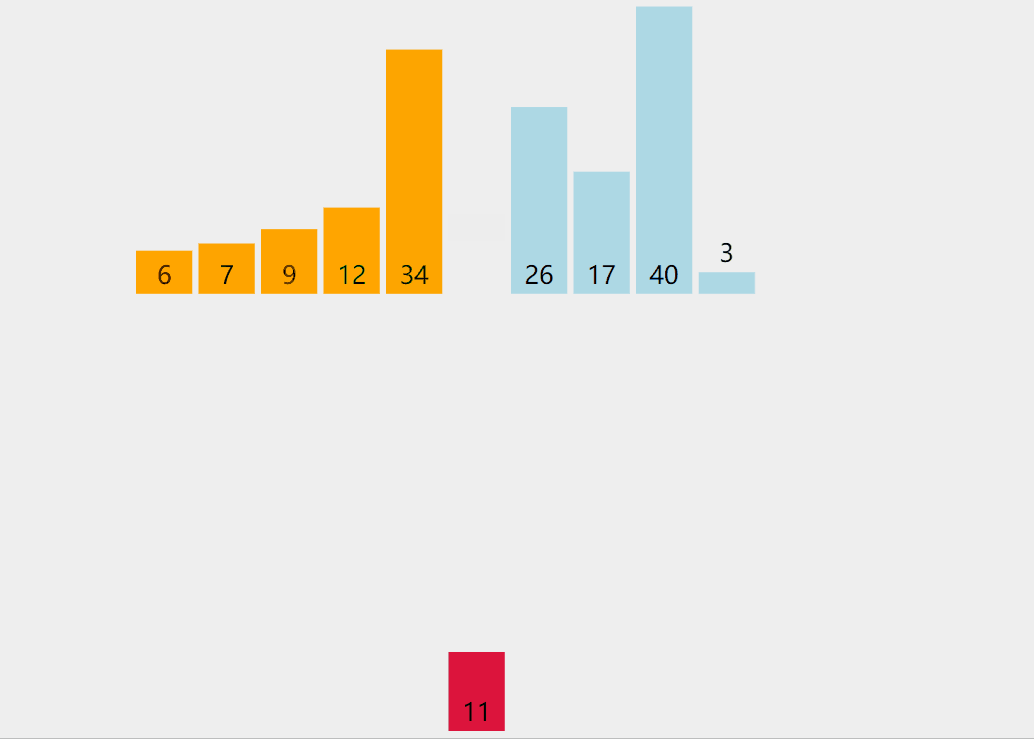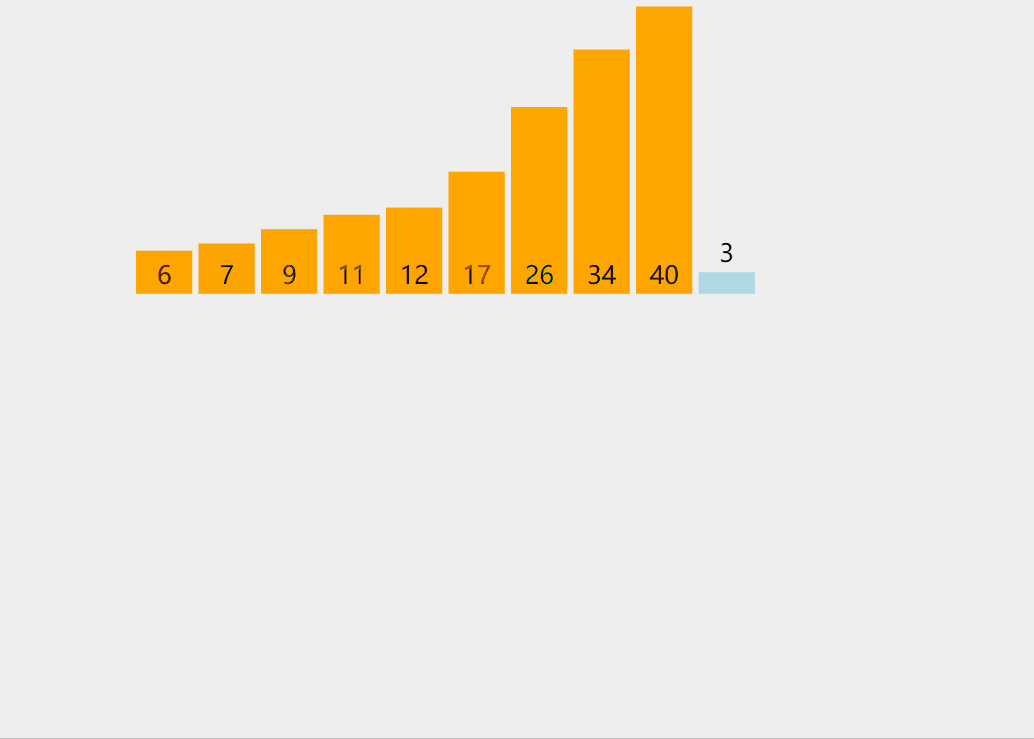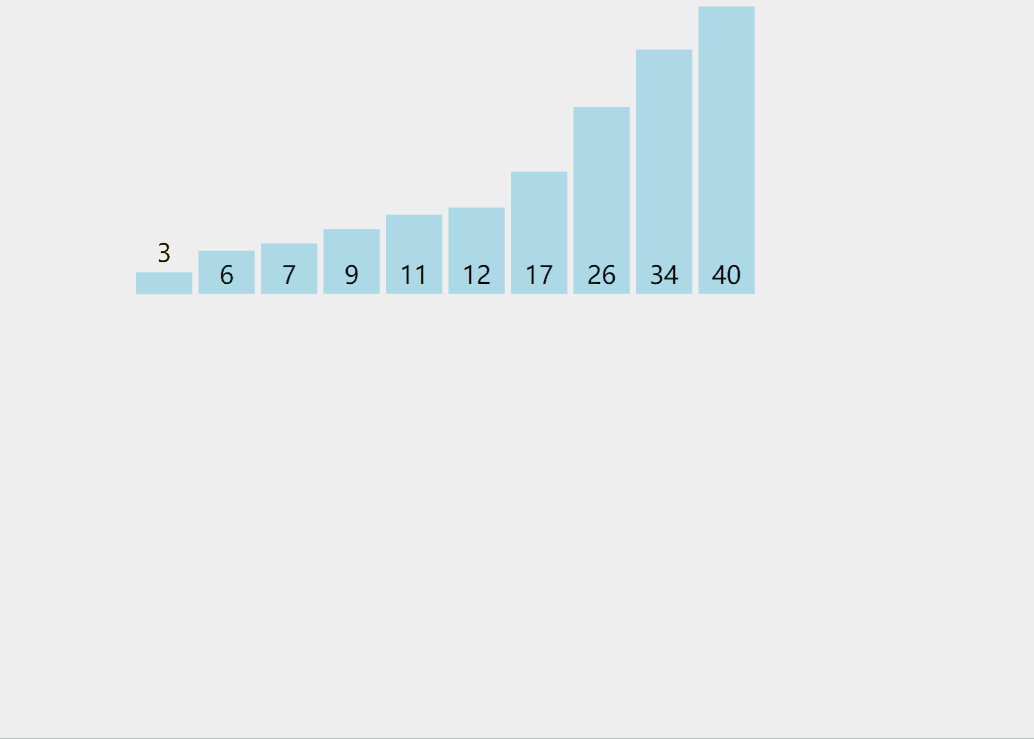
插入排序我们可以理解为，满足某一条件后，将当前的值插入到当前符合调节的位置上。通俗的来讲直接插入排序很像抓扑克，在我们抓扑克时候按顺序依次比较，符合条件后，再将扑克插入当位置上。（17张牌你能秒我？）走错过场了。我们先来看看动图。

是不是很像抓扑克？是不是很形象？我们来看看插入排序的代码

void InsertSort(int *a,int n)
{
    for(int i = 1; i < n; i ++)
    {
        int j = i - 1, k = a[i];
        while(j >= 0 && a[j] > k)
        {
            a[j + 1] = a[j];
            j --;
        }
        a[j + 1] = k;
    }
}

定义一个数组（int a[] = {7,12,6,34,9,11,26,17,40,3};），跑一下数据。

2、希尔排序

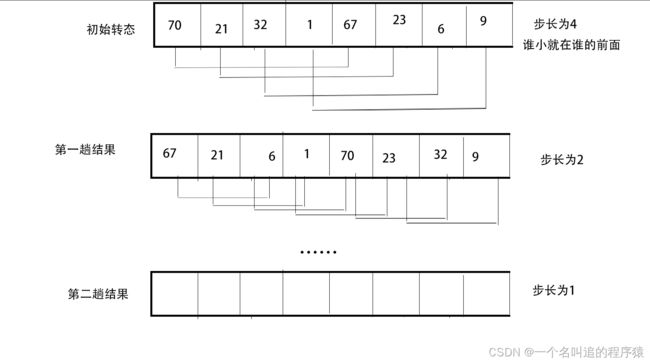
希尔排序就是将数组的长度对半分设置为步长，选择步长一一相对的元素，将小的放前面，做完一轮后，缩小步长（一般 缩小的直接除二），继续重复上面的的操作，我们来看看下面的的图。

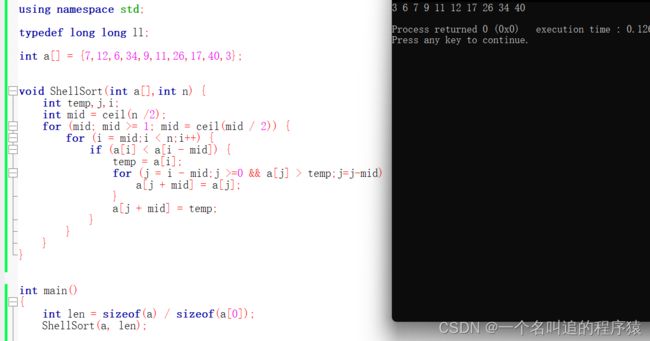
直接看代码咯（同样是和上面的数据）~

void ShellSort(int a[],int n) {
	int temp,j,i;
	int mid = ceil(n /2);
	for (mid; mid >= 1; mid = ceil(mid / 2)) {
		for (i = mid;i < n;i++) {
			if (a[i] < a[i - mid]) {
				temp = a[i];
				for (j = i - mid;j >=0 && a[j] > temp;j=j-mid) {
					a[j + mid] = a[j];
				}
				a[j + mid] = temp;
			}
		}
	}
}

二、选择排序

1、简单选择排序

简单选择排序就是我们扫描一个数组（下标 0 ~ n - 1），来找到当前最小值，找到之后，将最小值放入到最左边（下标为0），然后在扫描数组（1 ~ n - 1），找到最小值，放到最左边（下标为1）依次执行，来看看效果图。

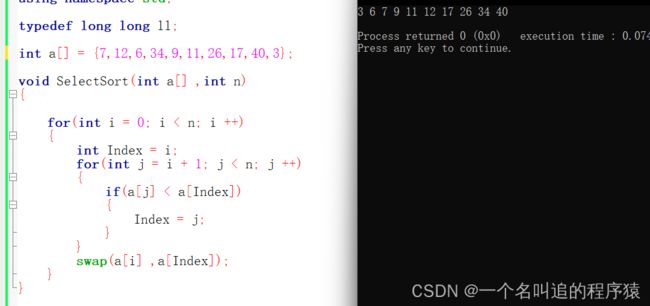
 是不是感觉如此的 so easy ？哈哈哈，我们来看看代码。

void SelectSort(int a[] ,int n)
{

	for(int i = 0; i < n; i ++)
    {
		int Index = i;
		for(int j = i + 1; j < n; j ++)
        {
			if(a[j] < a[Index])
			{
				Index = j;
			}
		}
		swap(a[i] ,a[Index]);
	}
}

 

2、堆排序

堆排序：堆它是一颗完全二叉树，我们要记得啥是小根堆？啥是大根堆？（ 孩子节点都大于等于父节点是小根堆，或者 孩子节点都小于等于父节点是大根堆）

因为是完全二叉树，则 i >= n / 2， i 表示叶子节点

先从 n / 2 的位置开始调整，大根堆，根节点位置都大于孩子节点，跟小则互调。

之后调整 n / 2 - 1节点，递推。如果互调后被调节点仍有孩子节点，则递归上述步骤

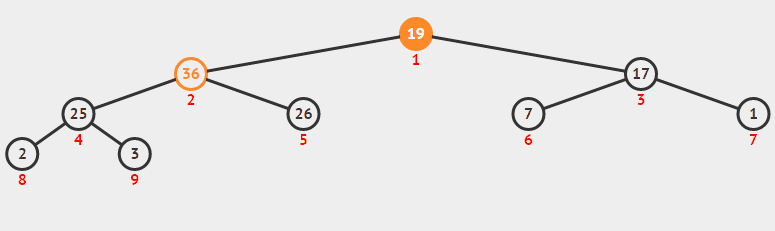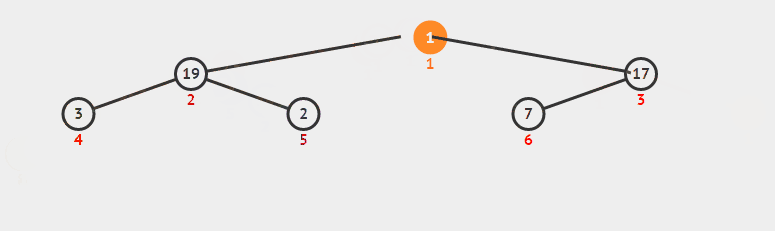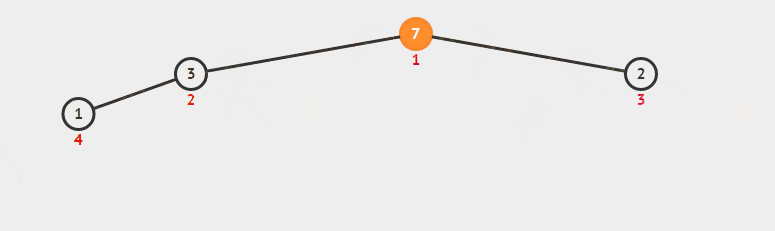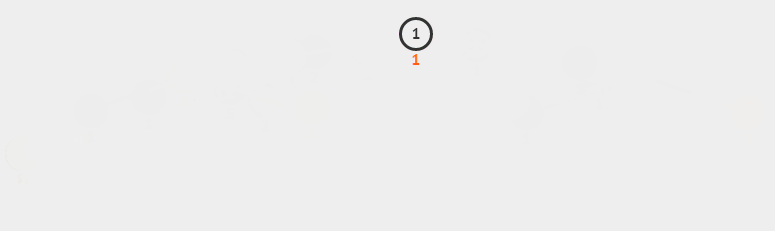
之后根节点与最后序列元素对调，并断开与父节点关系。一直递归下去，我们可以看下面的图加以理解。

看完图之后我们来看看代码。

void AdjustHeap(int a[], int r, int l){
        int left = 2 * r + 1;
        int right = 2 * r + 2;
        int Max = r;
        if( left < l && a[left] > a[Max])
                Max = left;
        if( right < l && a[right] > a[Max])
                Max = right;
        if(Max != r){
                swap( a[Max], a[r]);
                AdjustHeap(a, Max, l);
        }
}

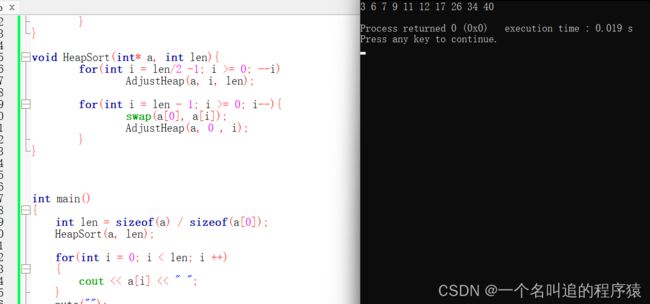
void HeapSort(int* a, int len){
        for(int i = len/2 -1; i >= 0; --i)
                AdjustHeap(a, i, len);

        for(int i = len - 1; i >= 0; i--){
                swap(a[0], a[i]);
                AdjustHeap(a, 0 , i);
        }
}

 

三、交换排序

1、冒泡排序

冒泡排序作为我们学 c 语言的第一个算法相信大家都不会陌生吧？它是选择两个相邻的数据进行比较 ，将小的数移到左边，然后再选择下一对两两相对的数进行比较，依次执行，看看效果图。

​

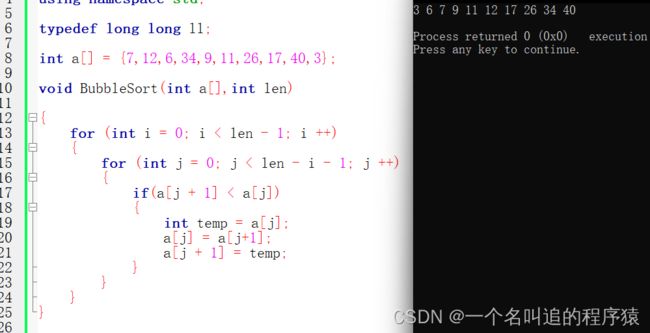
简单吧？有趣吗？我们直接来看看代码

void BubbleSort(int a[],int len)
                                
{
	for (int i = 0; i < len - 1; i ++)	
	{
		for (int j = 0; j < len - i - 1; j ++)	 
		{
			if(a[j + 1] < a[j])	
			{
				int temp = a[j];
				a[j] = a[j+1];
				a[j + 1] = temp;
			}
		}
	}	
}

​

2、快速排序

快速排序的理解：每次选择数组的第一个元素作为记号，大于这个记号的都放在它的右边，凡是小于这个记号的都放在它的左边，我们有两个变量 i 和 j ，设第一个元素作为记号 ，i 指向序列的最左边（下标为 0），j 指向序列的最右边（下标为n - 1），j 从右往左走（j --），i 从左往右走(i ++)，直到 j 找到小于记号就停止，i 找到大于记号就停止，交换 i 和 j 指向的两个数，j 继续往左走，i 继续往右走,如果 i 和 j 相遇(i == j)，则 i 或 j 上的元素与记号交换，则这一轮排序结束，然后继续执行以上操作。

​

 加油呀~都看到这里了，再坚持坚持~

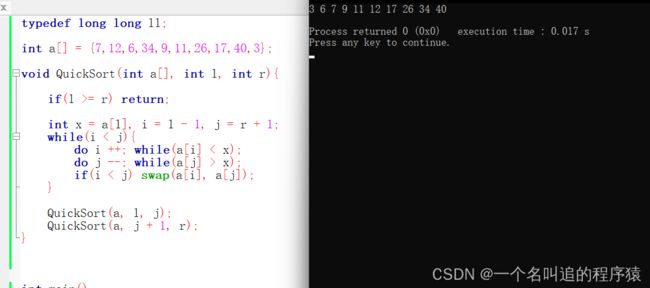
话不多说，直接看代码

void QuickSort(int a[], int l, int r){

    if(l >= r) return;

    int x = a[l], i = l - 1, j = r + 1;
    while(i < j){
        do i ++; while(a[i] < x);
        do j --; while(a[j] > x);
        if(i < j) swap(a[i], a[j]);
    }

    QuickSort(a, l, j);
    QuickSort(a, j + 1, r);
}

​

四、归并排序

归并排序是将序列分成两个小大致的两个子序列，再分别对两个序列调用归并排序，最终将排序好的序列合并成要求的排序好的序列（解体，升级）。

​

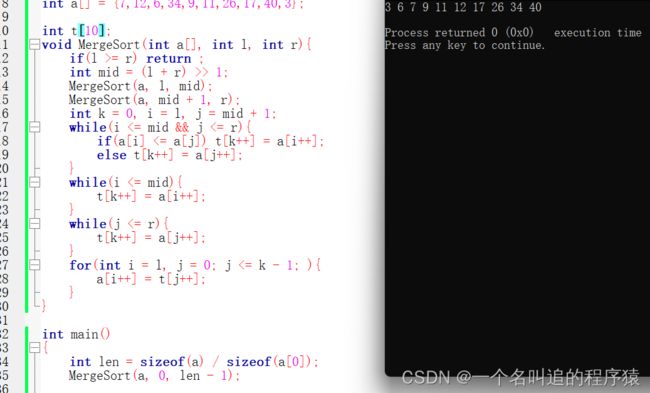
我们来看看代码

void MergeSort(int a[], int l, int r){
    if(l >= r) return ;
    int mid = (l + r) >> 1;
    MergeSort(a, l, mid);
    MergeSort(a, mid + 1, r);
    int k = 0, i = l, j = mid + 1;
    while(i <= mid && j <= r){
        if(a[i] <= a[j]) t[k++] = a[i++];
        else t[k++] = a[j++];
    }
    while(i <= mid){
        t[k++] = a[i++];
    }
    while(j <= r){
        t[k++] = a[j++];
    }
    for(int i = l, j = 0; j <= k - 1; ){
        a[i++] = t[j++];
    }
}

​

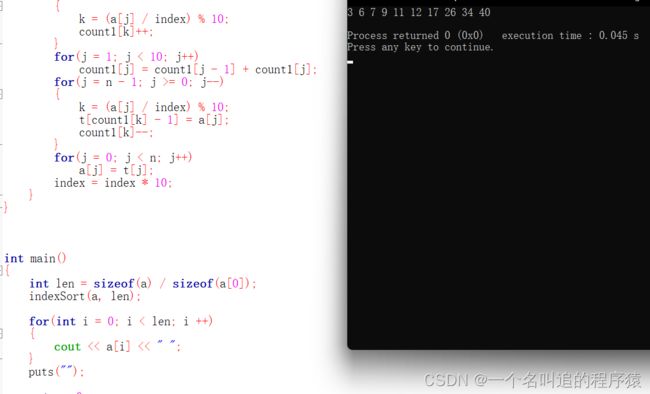
五、基数排序

基数排序是一种非比较型整数排序算法，原理是将众多数字按位分隔后进行排序。将所有待比较的数字（正整数）统一为同一长度（即最长的那一个位数），位数不够的数字前面补0（如最大为数是3，那么 8 就是 008）；按照从个位，十位，百位······从低到高的顺序进行排序（可以理解为切尾巴）；完成从低位到高位的排序后，待排序数字也就完成了排序，我们来看看效果图。

​

 快结束了，再坚持坚持，加油加油~

代码如下

int MaxDigit(int a[], int n)
{
    int t = 1;
    int p = 10;
    for(int i = 0; i < n; ++i)
    {
        while(a[i] >= p)
        {
            p *= 10;
            ++ t;
        }
    }
    return t;
}
void indexSort(int a[], int n)
{
    int d = MaxDigit(a, n);
    int t[n];
    int count1[10];
    int i, j, k;
    int index = 1;
    for(i = 1; i <= d; i++)
    {
        for(j = 0; j < 10; j++)
            count1[j] = 0;
        for(j = 0; j < n; j++)
        {
            k = (a[j] / index) % 10;
            count1[k]++;
        }
        for(j = 1; j < 10; j++)
            count1[j] = count1[j - 1] + count1[j];
        for(j = n - 1; j >= 0; j--)
        {
            k = (a[j] / index) % 10;
            t[count1[k] - 1] = a[j];
            count1[k]--;
        }
        for(j = 0; j < n; j++)
            a[j] = t[j];
        index = index * 10;
    }
}

​

总结 

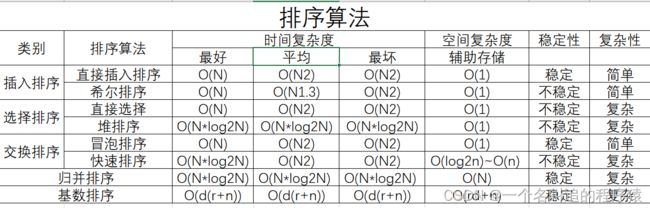
这里作出总结，在上面这些排序中，我们可以看到即使是不一样的排序它们都有各自的优势，有各自的时间复杂度与空间复杂度。那么下面我们来看看。

（求关注）持续更新中……