![]()
- 作者:韩信子@ShowMeAI,路遥@ShowMeAI,奇异果@ShowMeAI
- 教程地址:http://www.showmeai.tech/tutorials/36
- 本文地址:http://www.showmeai.tech/article-detail/240
- 声明:版权所有,转载请联系平台与作者并注明出处
- 收藏ShowMeAI查看更多精彩内容
ShowMeAI为斯坦福CS224n《自然语言处理与深度学习(Natural Language Processing with Deep Learning)》课程的全部课件,做了中文翻译和注释,并制作成了GIF动图!
本讲内容的深度总结教程可以在这里 查看。视频和课件等资料的获取方式见文末。
引言
(本篇内容也可以参考ShowMeAI的对吴恩达老师课程的总结文章深度学习教程 | 序列模型与RNN网络)
概述
介绍一个新的NLP任务
- Language Modeling 语言模型
介绍一个新的神经网络家族
- Recurrent Neural Networks (RNNs)
1.语言模型
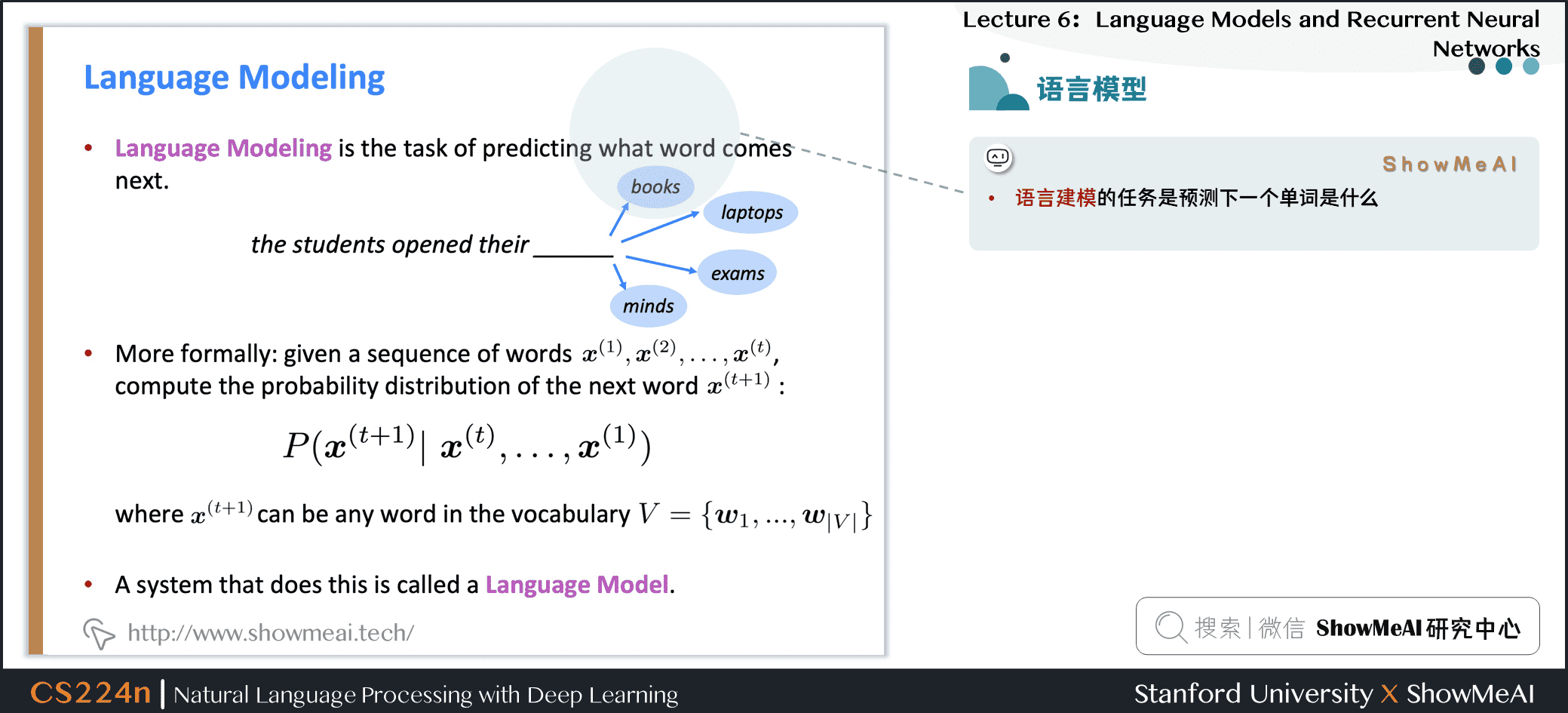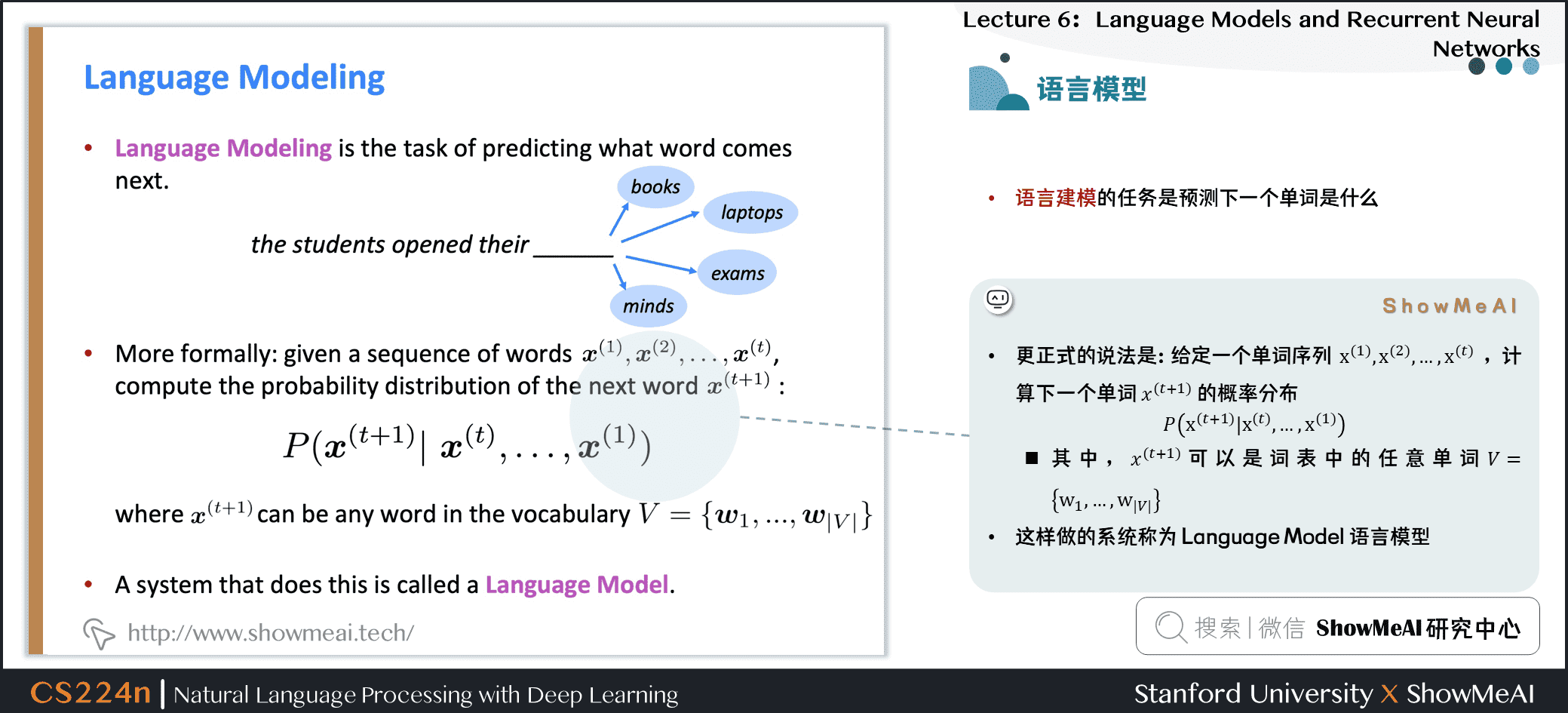
1.1 语言模型
语言建模的任务是预测下一个单词是什么
更正式的说法是:给定一个单词序列 \(\boldsymbol{x}^{(1)}, \boldsymbol{x}^{(2)}, \ldots, \boldsymbol{x}^{(t)}\),计算下一个单词 \(x^{(t+1)}\) 的概率分布:
$$ P\left(\boldsymbol{x}^{(t+1)} \mid \boldsymbol{x}^{(t)}, \ldots, \boldsymbol{x}^{(1)}\right) $$
- 其中,\(x^{(t+1)}\) 可以是词表中的任意单词 \(V=\left{\boldsymbol{w}_{1}, \ldots, \boldsymbol{w}_{|V|}\right}\)
- 这样做的系统称为 Language Model 语言模型
1.2 语言模型
- 还可以将语言模型看作评估一段文本是自然句子(通顺度)的概率
- 例如,如果我们有一段文本 \(x^{(1)},\dots,x^{(T)}\),则这段文本的概率(根据语言模型)为
$$ \begin{aligned} P\left(\boldsymbol{x}^{(1)}, \ldots, \boldsymbol{x}^{(T)}\right) &=P\left(\boldsymbol{x}^{(1)}\right) \times P\left(\boldsymbol{x}^{(2)} \mid \boldsymbol{x}^{(1)}\right) \times \cdots \times P\left(\boldsymbol{x}^{(T)} \mid \boldsymbol{x}^{(T-1)}, \ldots, \boldsymbol{x}^{(1)}\right) \\ &=\prod_{t=1}^{T} P\left(\boldsymbol{x}^{(t)} \mid \boldsymbol{x}^{(t-1)}, \ldots, \boldsymbol{x}^{(1)}\right) \end{aligned} $$
- 语言模型提供的是 \(\prod_{t=1}^{T} P\left(\boldsymbol{x}^{(t)} \mid \boldsymbol{x}^{(t-1)}, \ldots, \boldsymbol{x}^{(1)}\right)\)
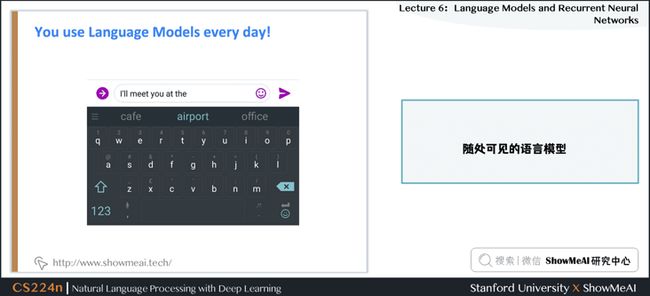
1.3 随处可见的语言模型
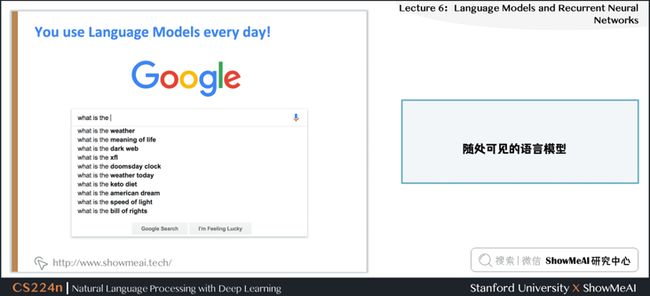
1.4 随处可见的语言模型
1.5 n-gram 语言模型
the students opened their __
- 问题:如何学习一个语言模型?
- 回答(深度学习之前的时期):学习一个 n-gram 语言模型
定义:n-gram是一个由 \(n\) 个连续单词组成的块
- unigrams:
the,students,opened,their - bigrams:
the students,students opened,opened their - trigrams:
the students opened,students opened their - 4-grams:
the students opened their
- unigrams:
- 想法:收集关于不同 n-gram 出现频率的统计数据,并使用这些数据预测下一个单词
1.6 n-gram 语言模型
- 首先,我们做一个简化假设:\(x^{(t+1)}\) 只依赖于前面的 \(n-1\) 个单词
$$ \begin{aligned} P\left(\boldsymbol{x}^{(t+1)} \mid \boldsymbol{x}^{(t)}, \ldots, \boldsymbol{x}^{(1)}\right) & =P\left(\boldsymbol{x}^{(t+1)} \mid \boldsymbol{x}^{(t)}, \ldots, \boldsymbol{x}^{(t-n+2)}\right)\\ &=\frac{P\left(\boldsymbol{x}^{(t+1)}, \boldsymbol{x}^{(t)}, \ldots, \boldsymbol{x}^{(t-n+2)}\right)}{P\left(\boldsymbol{x}^{(t)}, \ldots, \boldsymbol{x}^{(t-n+2)}\right)} \end{aligned} $$
- 问题:如何得到n-gram和(n-1)-gram的概率?
- 回答:通过在一些大型文本语料库中计算它们(统计近似)
$$ \approx \frac{\operatorname{count}\left(\boldsymbol{x}^{(t+1)}, \boldsymbol{x}^{(t)}, \ldots, \boldsymbol{x}^{(t-n+2)}\right)}{\operatorname{count}\left(\boldsymbol{x}^{(t)}, \ldots, \boldsymbol{x}^{(t-n+2)}\right)} $$
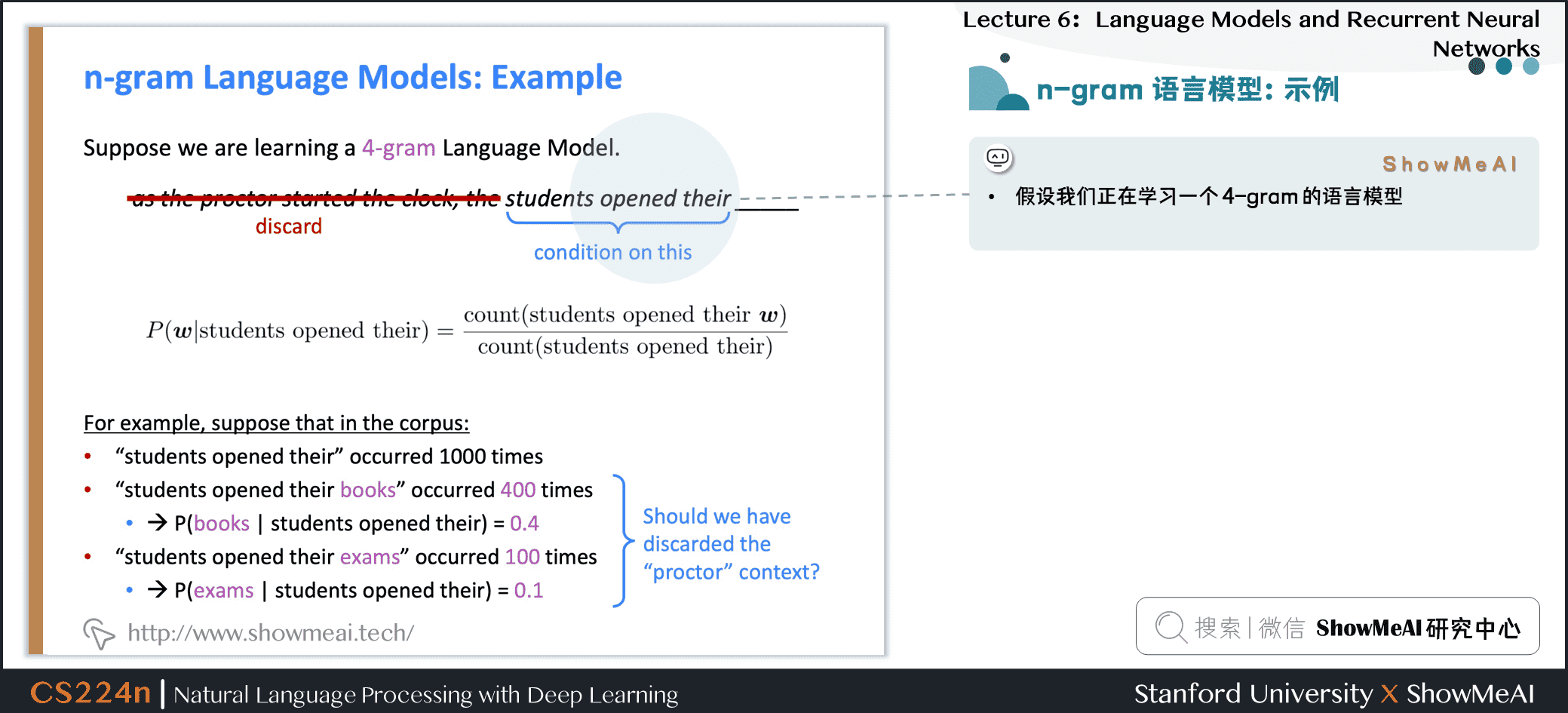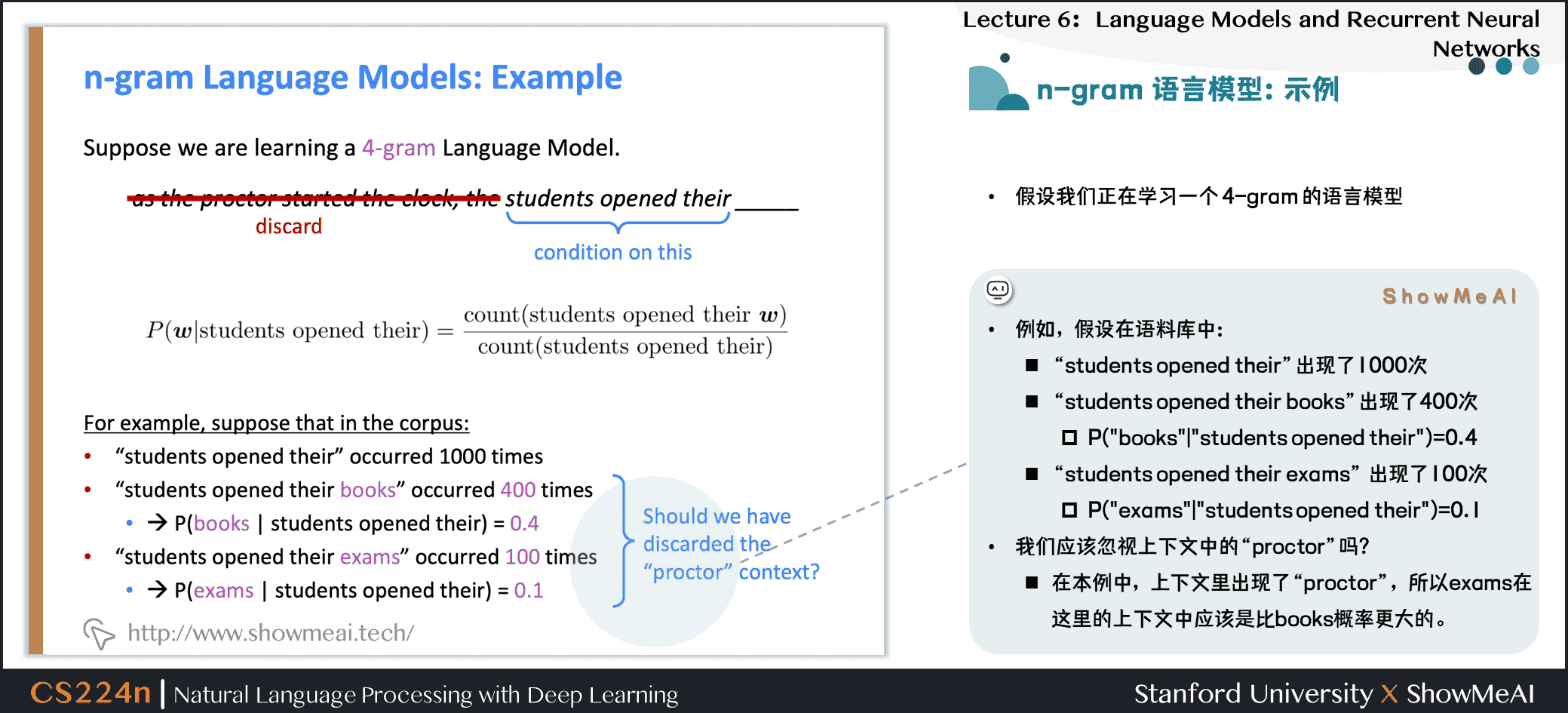
1.7 n-gram 语言模型:示例
假设我们正在学习一个 4-gram 的语言模型
例如,假设在语料库中:
students opened their出现了\(1000\)次students opened their books出现了\(400\)次
$$ P(\text{books} \mid \text{students opened their})=0.4 $$
students opened their exams出现了\(100\)次
$$ P( \text{exams} \mid \text{students opened their})=0.1 $$
我们应该忽视上下文中的
proctor吗?- 在本例中,上下文里出现了
proctor,所以exams在这里的上下文中应该是比books概率更大的。
- 在本例中,上下文里出现了
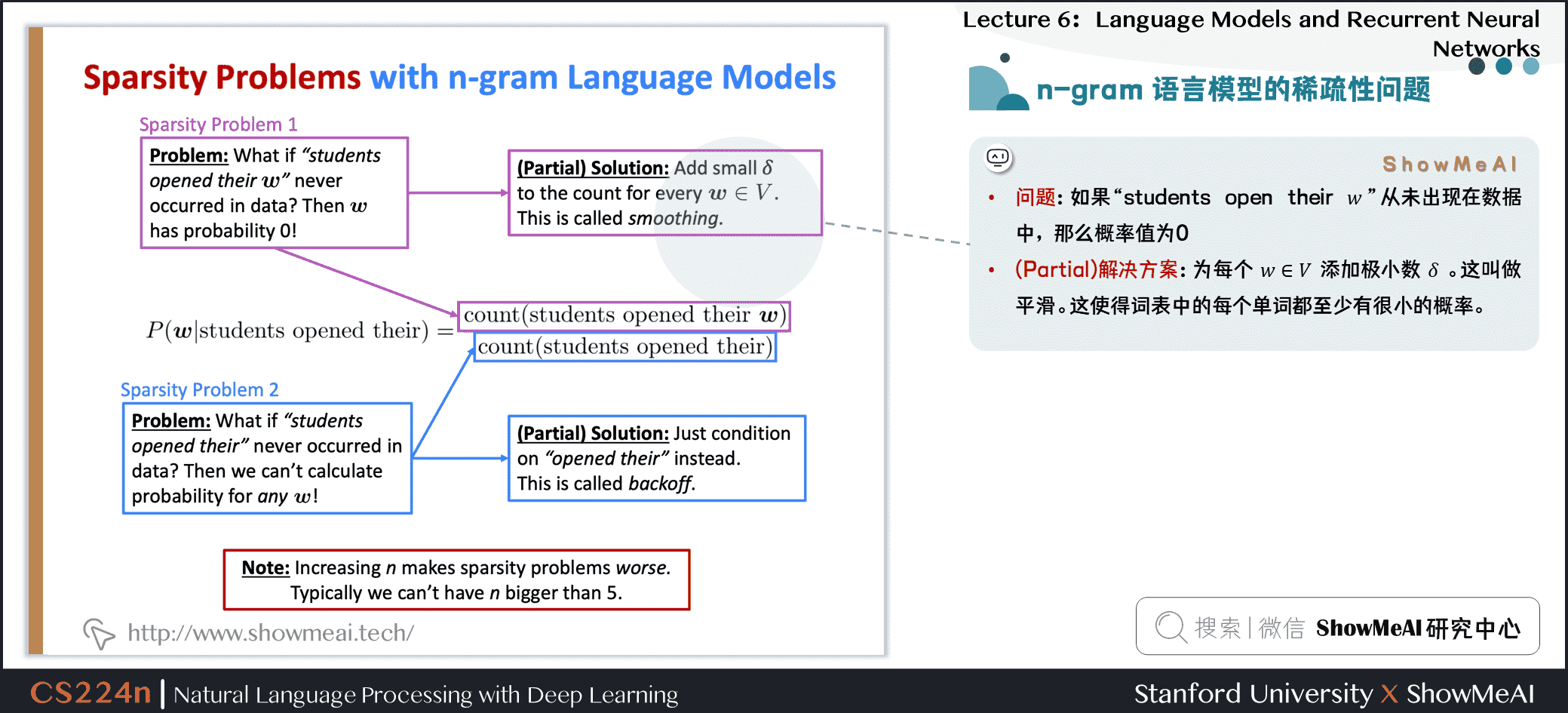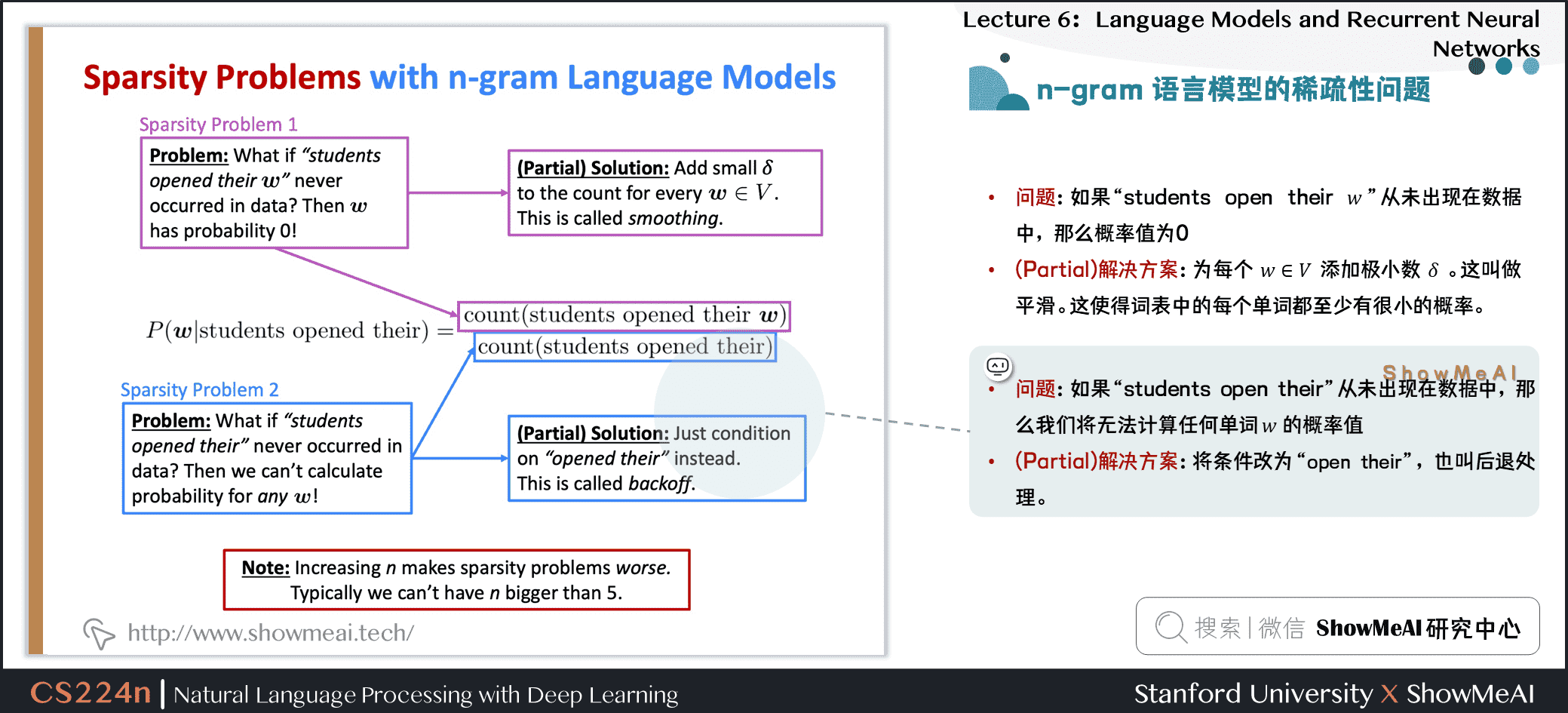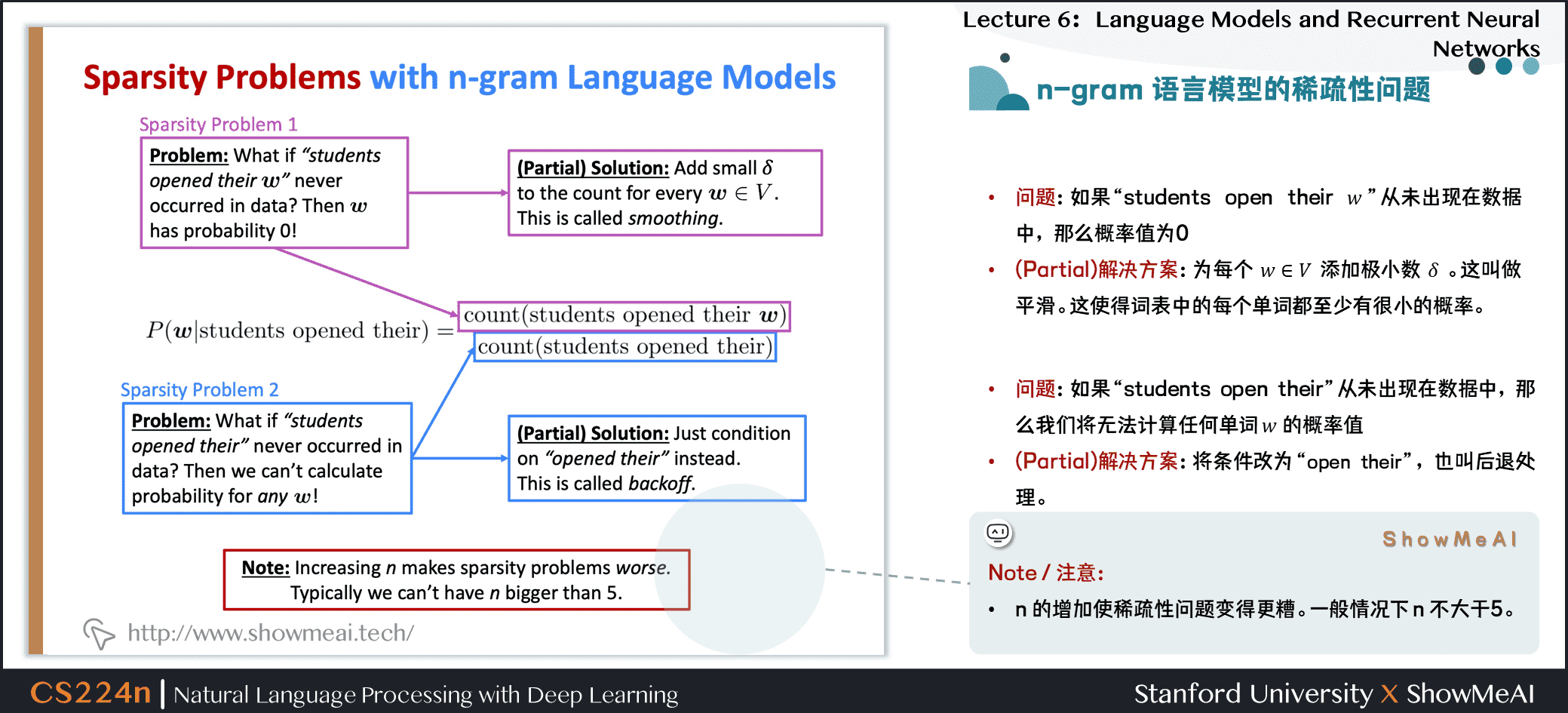
1.8 n-gram语言模型的稀疏性问题
- 问题1:如果
students open their ww从未出现在数据中,那么概率值为\(0\) - (Partial)解决方案:为每个 \(w \in V\) 添加极小数 \(\delta\) ,这叫做平滑。这使得词表中的每个单词都至少有很小的概率。
- 问题2:如果
students open their从未出现在数据中,那么我们将无法计算任何单词 \(w\) 的概率值 - (Partial)解决方案:将条件改为
open their,也叫做后退处理。
- Note/注意: \(n\) 的增加使稀疏性问题变得更糟。一般情况下 \(n\) 不能大于\(5\)。
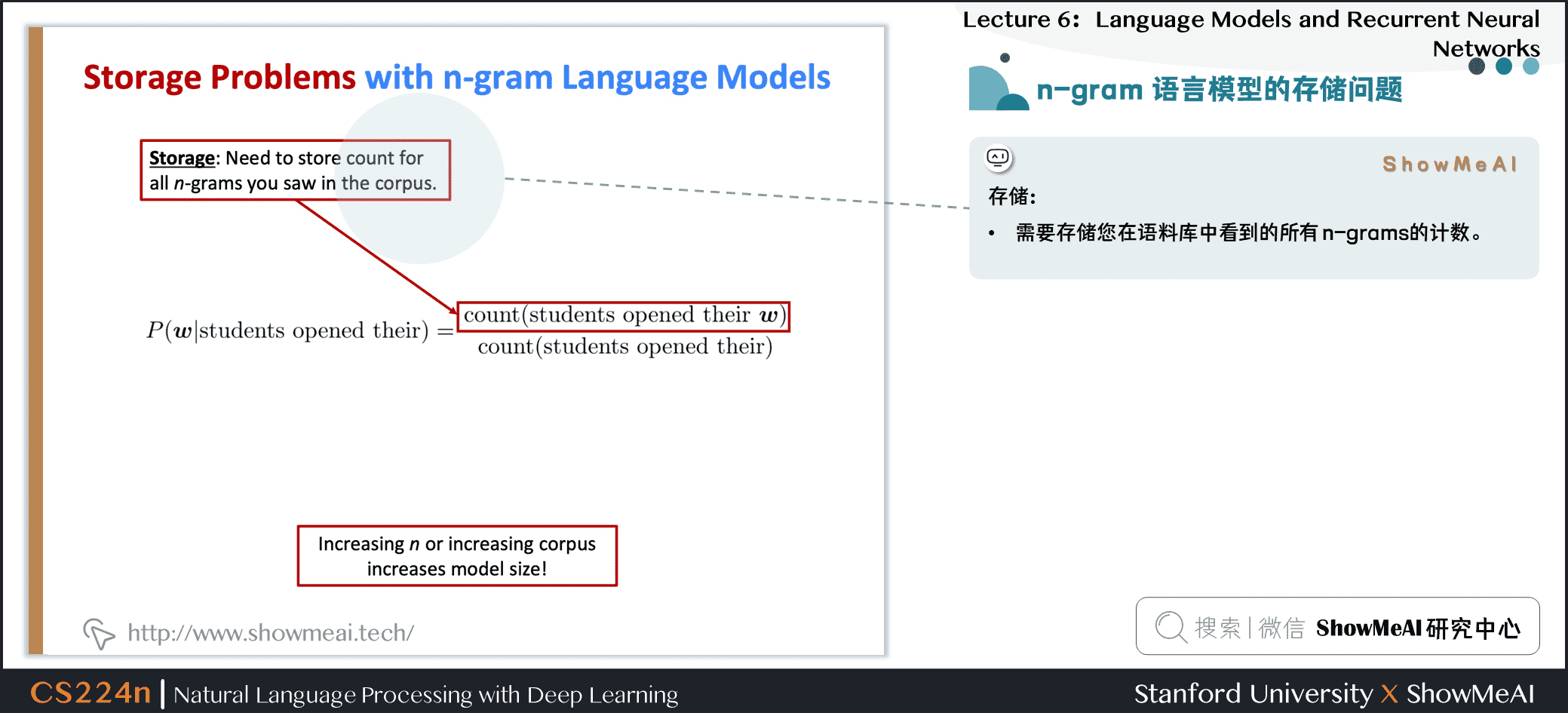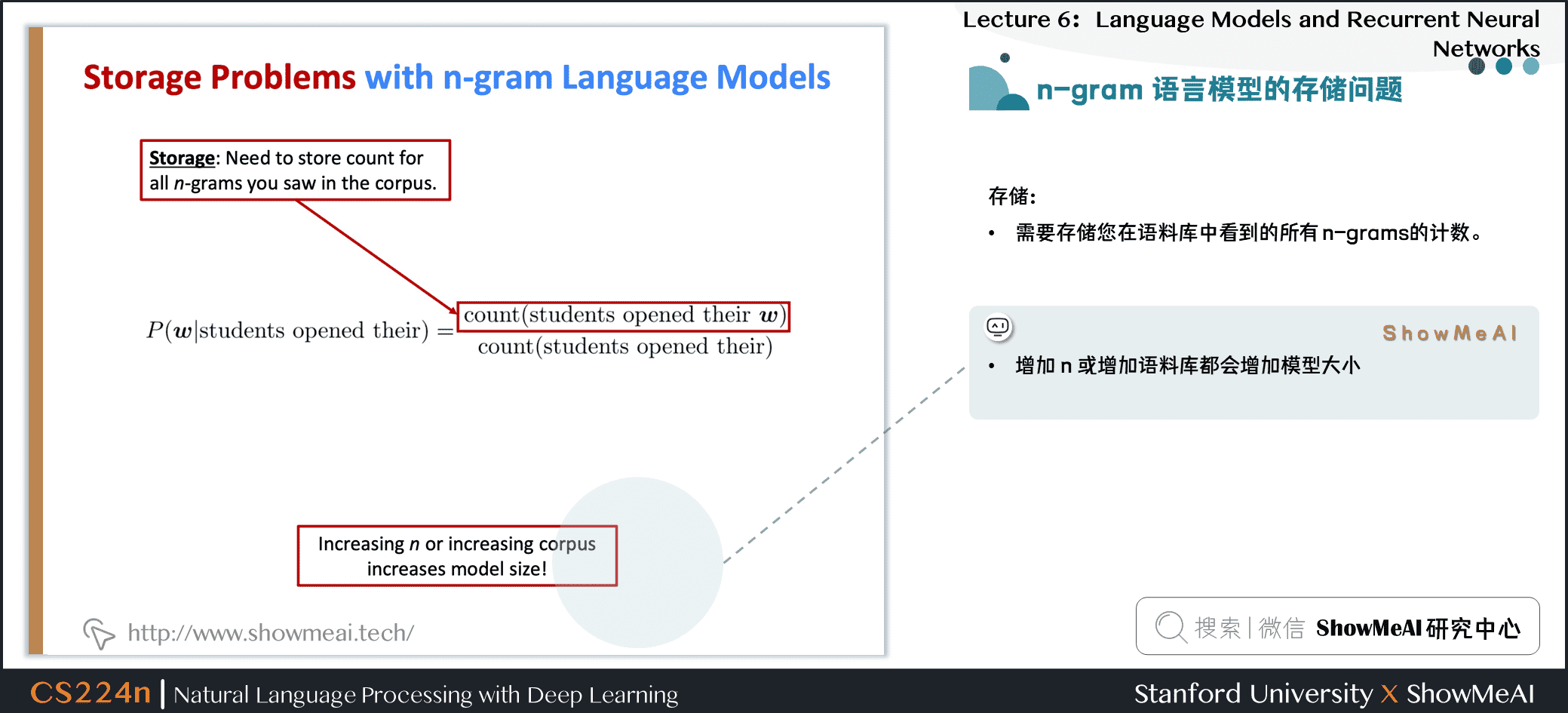
1.9 n-gram语言模型的存储问题
问题:需要存储你在语料库中看到的所有 n-grams 的计数
增加 \(n\) 或增加语料库都会增加模型大小
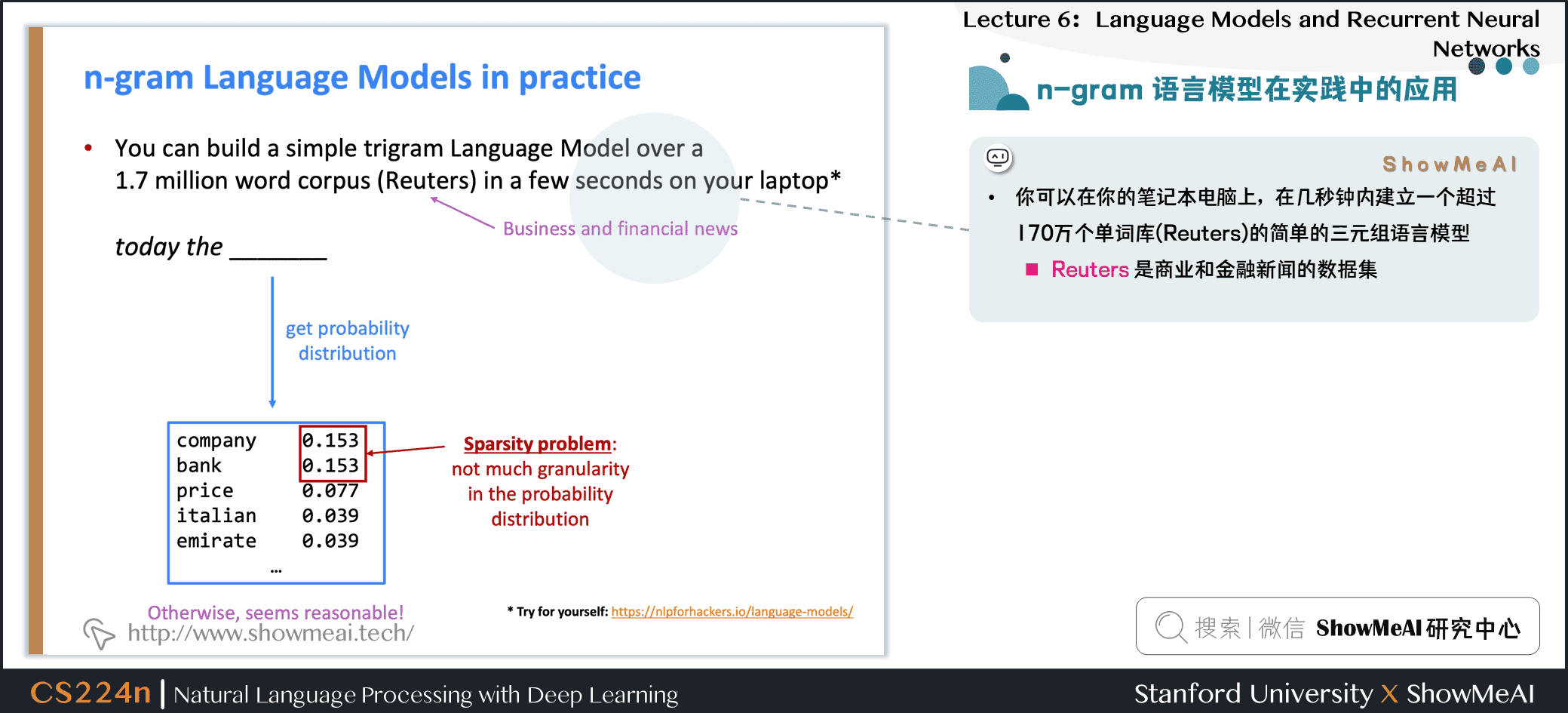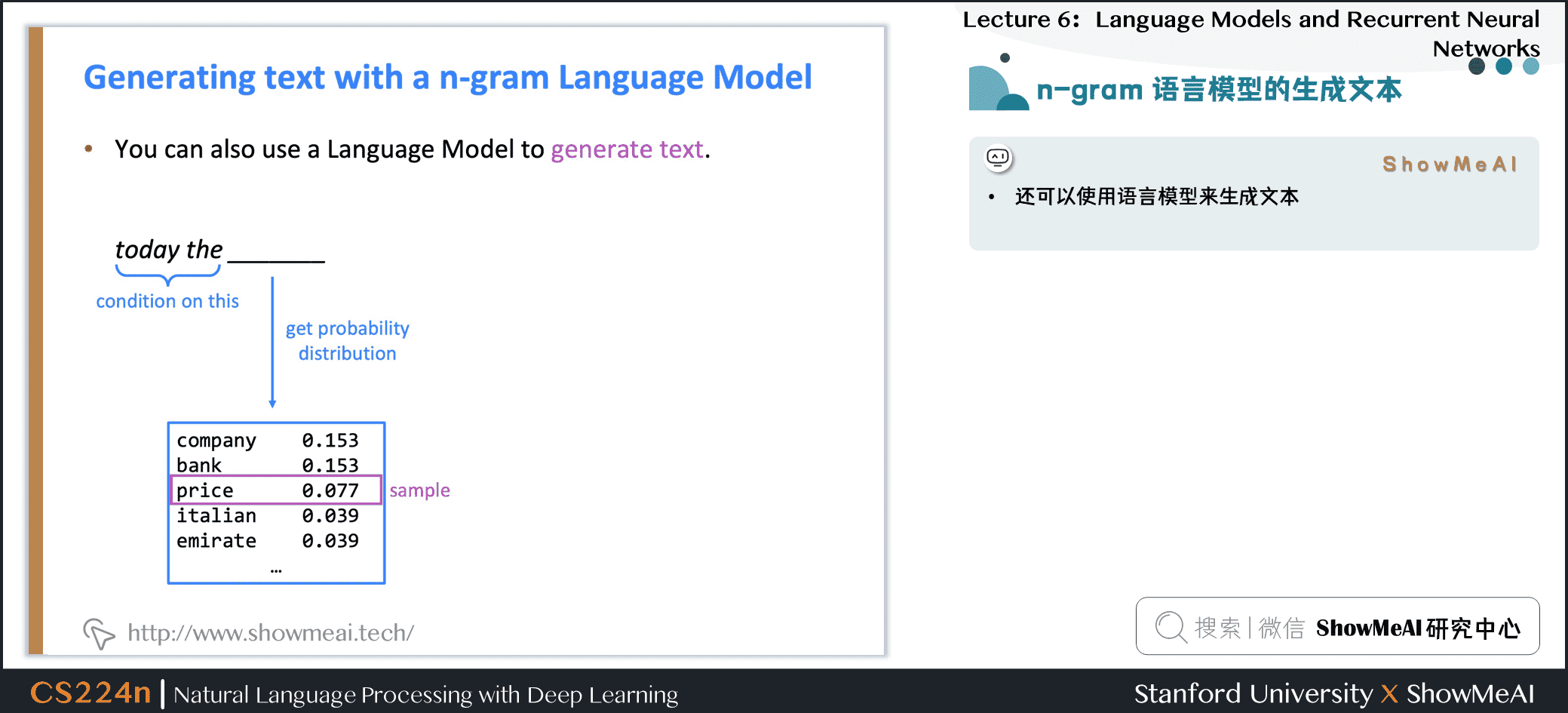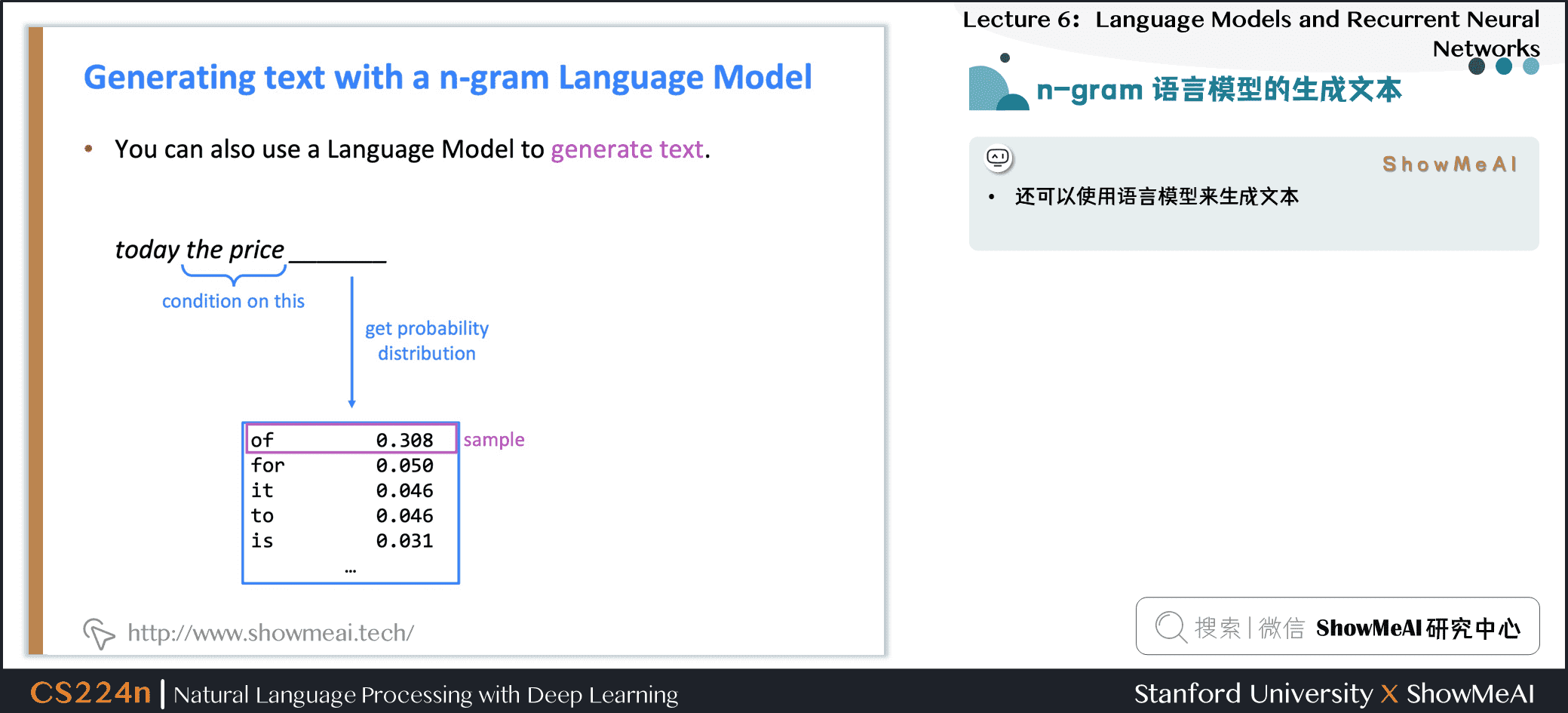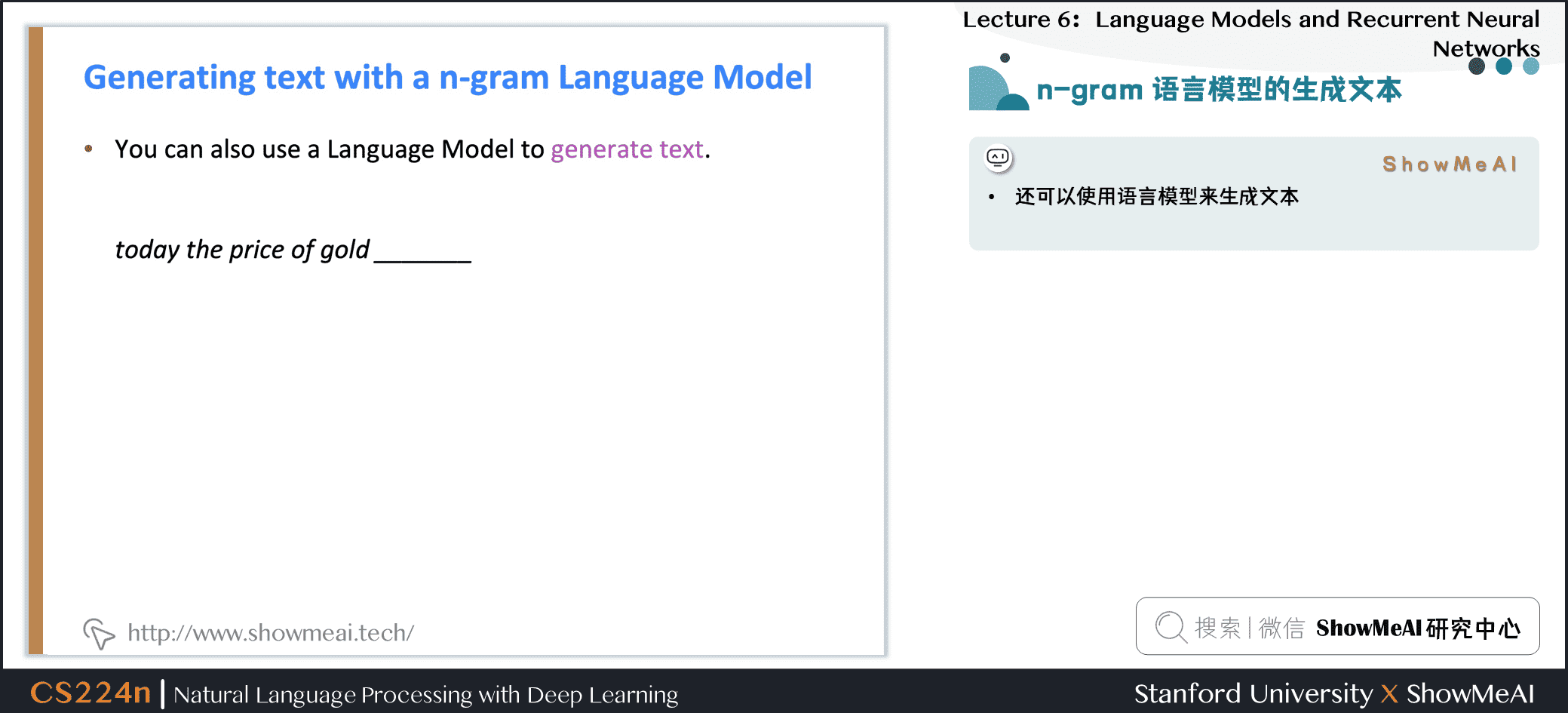
1.10 n-gram 语言模型在实践中的应用
Try for yourself: https://nlpforhackers.io/lang...
你可以在你的笔记本电脑上,在几秒钟内建立一个超过170万个单词库(Reuters)的简单的三元组语言模型
- Reuters 是 商业和金融新闻的数据集
稀疏性问题:
- 概率分布的粒度不大。
today the company和today he bank都是4/26,都只出现过四次
1.11 n-gram语言模型的生成文本
- 可以使用语言模型来生成文本
- 使用trigram运行以上生成过程时,会得到上图左侧的文本
- 令人惊讶的是其具有语法但是是不连贯的。如果我们想要很好地模拟语言,我们需要同时考虑三个以上的单词。但增加 \(n\) 使模型的稀疏性问题恶化,模型尺寸增大
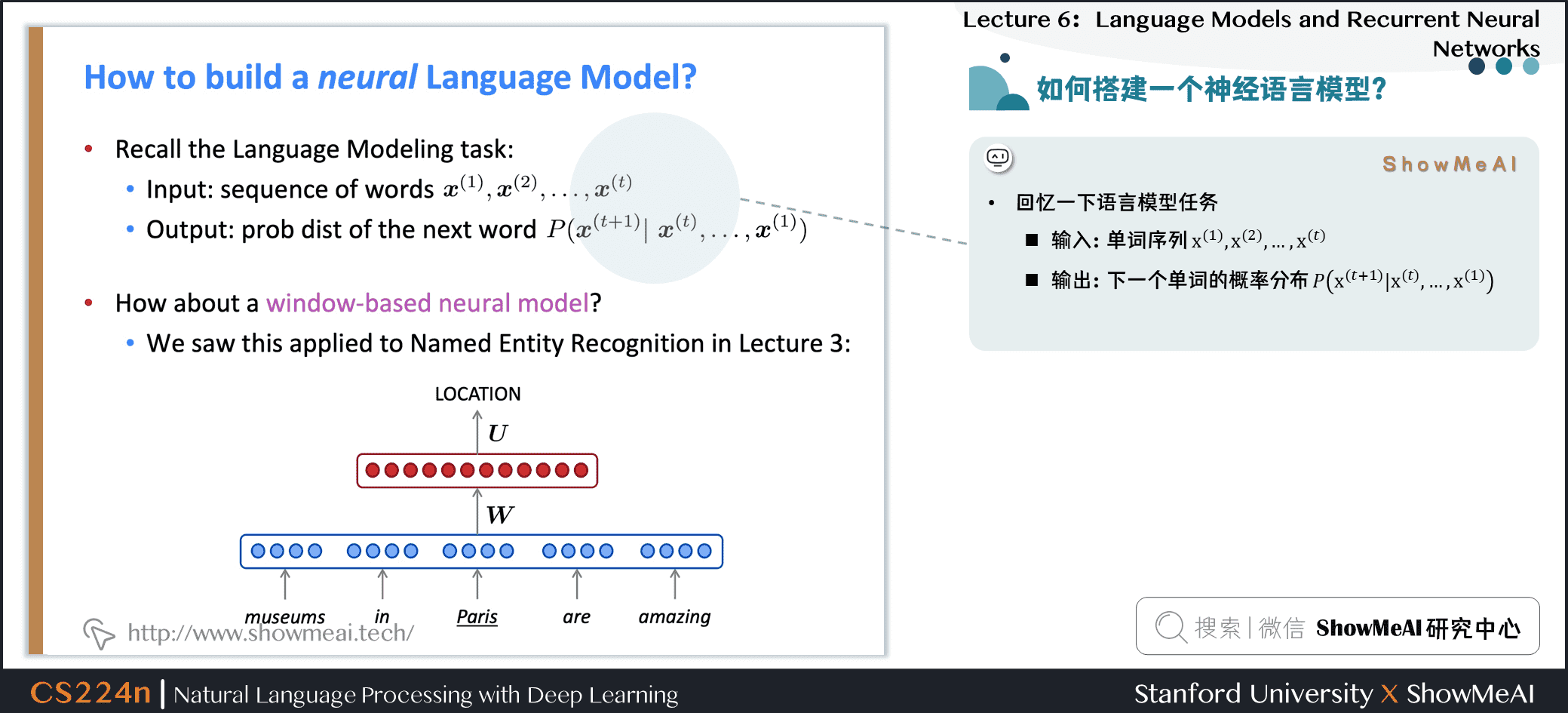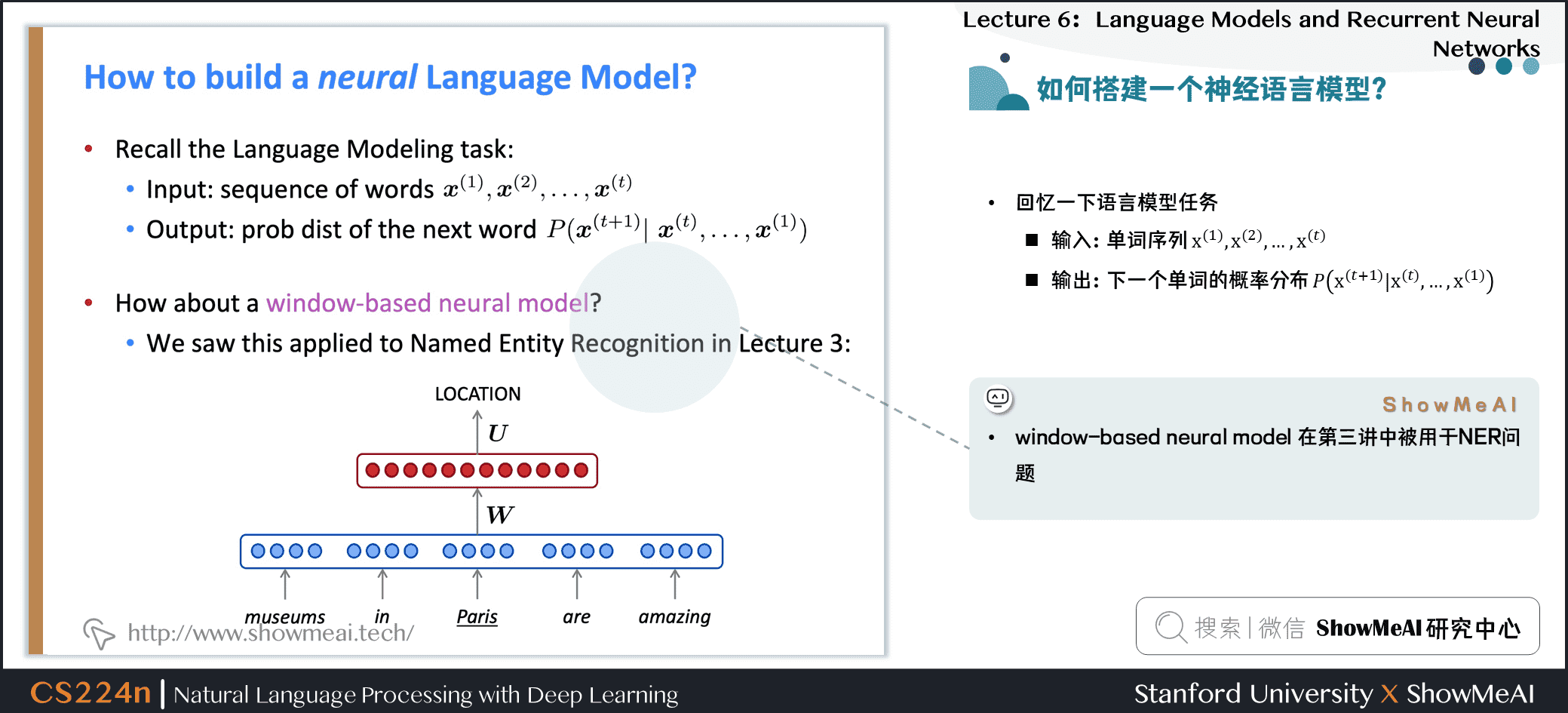
1.12 如何搭建一个神经语言模型?
回忆一下语言模型任务
- 输入:单词序列 \(\boldsymbol{x}^{(1)}, \boldsymbol{x}^{(2)}, \ldots, \boldsymbol{x}^{(t)}\)
- 输出:下一个单词的概\(P\left(\boldsymbol{x}^{(t+1)} \mid \boldsymbol{x}^{(t)}, \ldots, \boldsymbol{x}^{(1)}\right)\)率分布
- window-based neural model 在第三讲中被用于NER问题
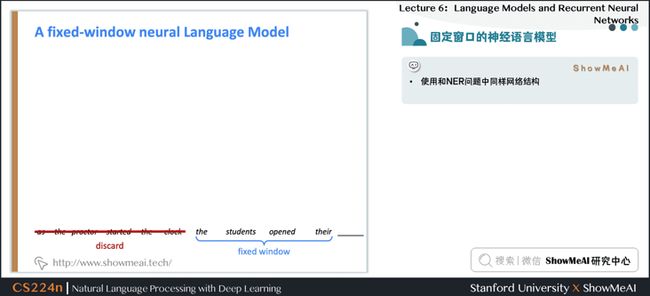
1.13 固定窗口的神经语言模型
- 使用和NER问题中同样网络结构
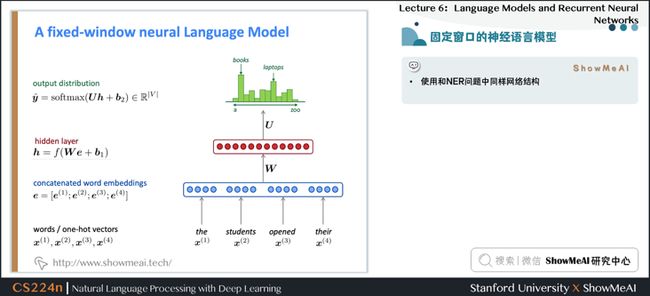
1.14 固定窗口的神经语言模型
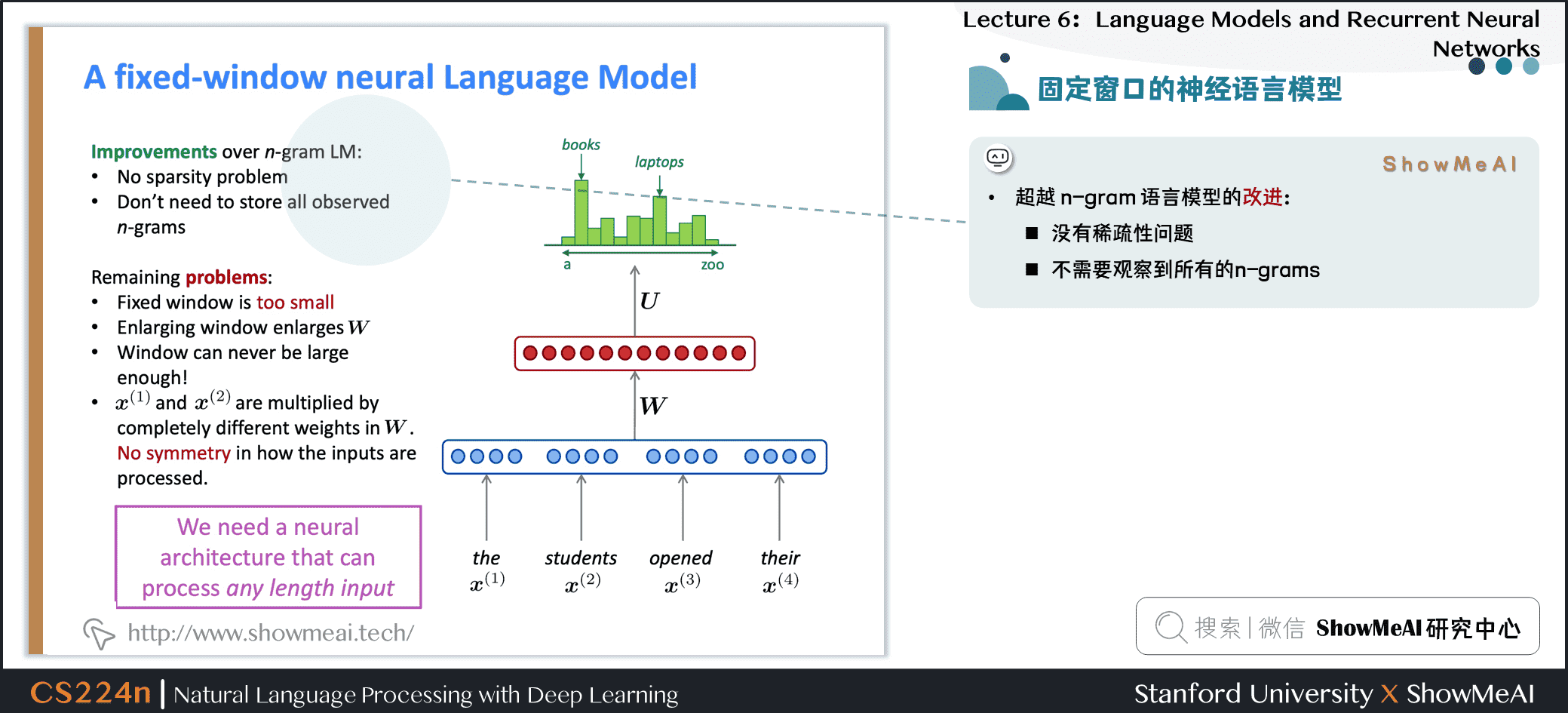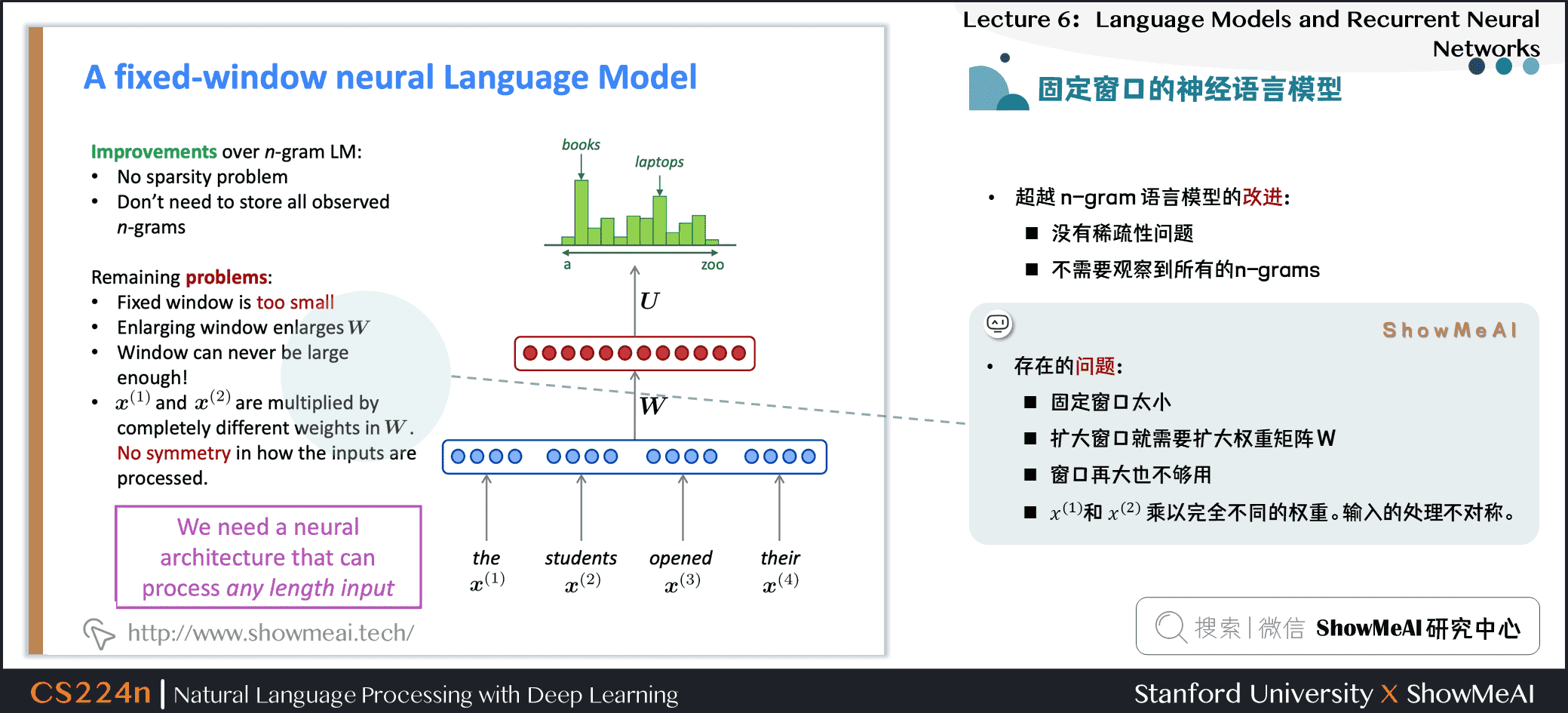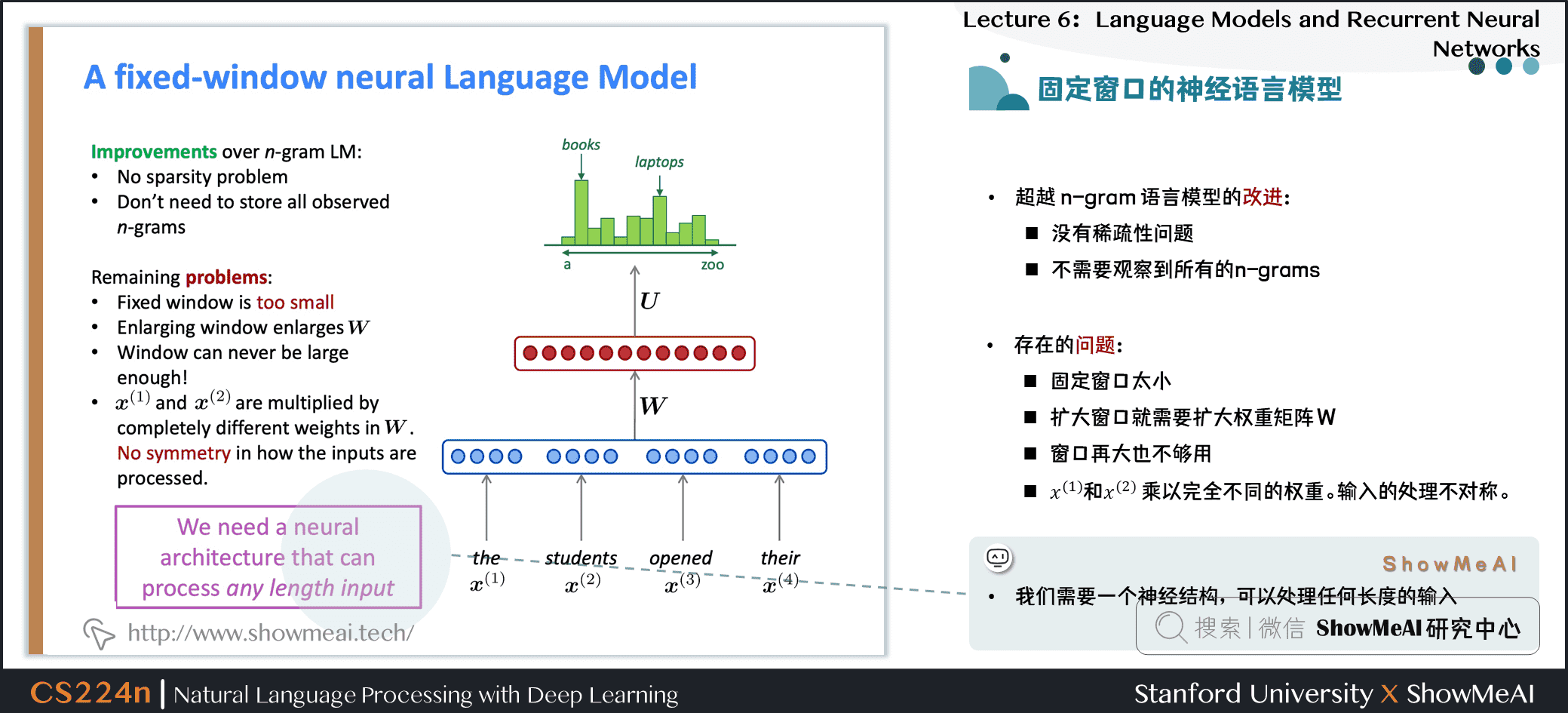
1.15 固定窗口的神经语言模型
超越 n-gram 语言模型的改进
- 没有稀疏性问题
- 不需要观察到所有的n-grams
NNLM存在的问题
- 固定窗口太小
- 扩大窗口就需要扩大权重矩阵\(W\)
- 窗口再大也不够用
- \(x^{(1)}\)和 \(x^{(2)}\) 乘以完全不同的权重。输入的处理不对称
我们需要一个神经结构,可以处理任何长度的输入
2.循环神经网络(RNN)
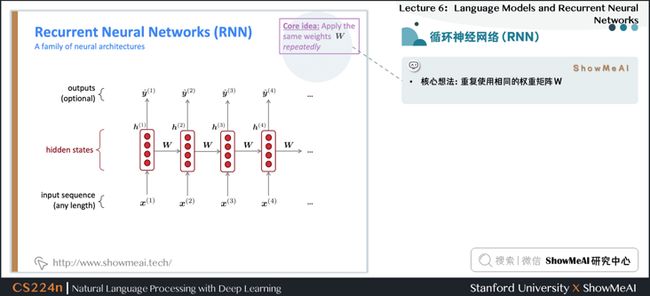
2.1 循环神经网络(RNN)
- 核心想法:重复使用相同的权重矩阵\(W\)
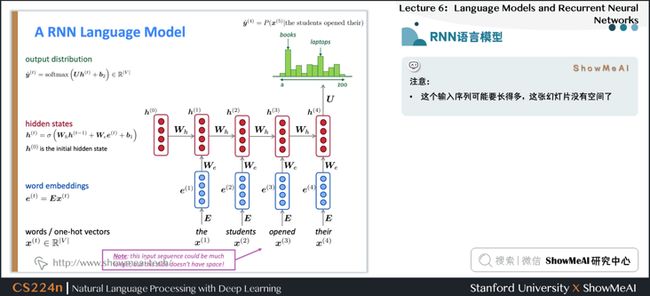
2.2 RNN语言模型
2.3 RNN语言模型
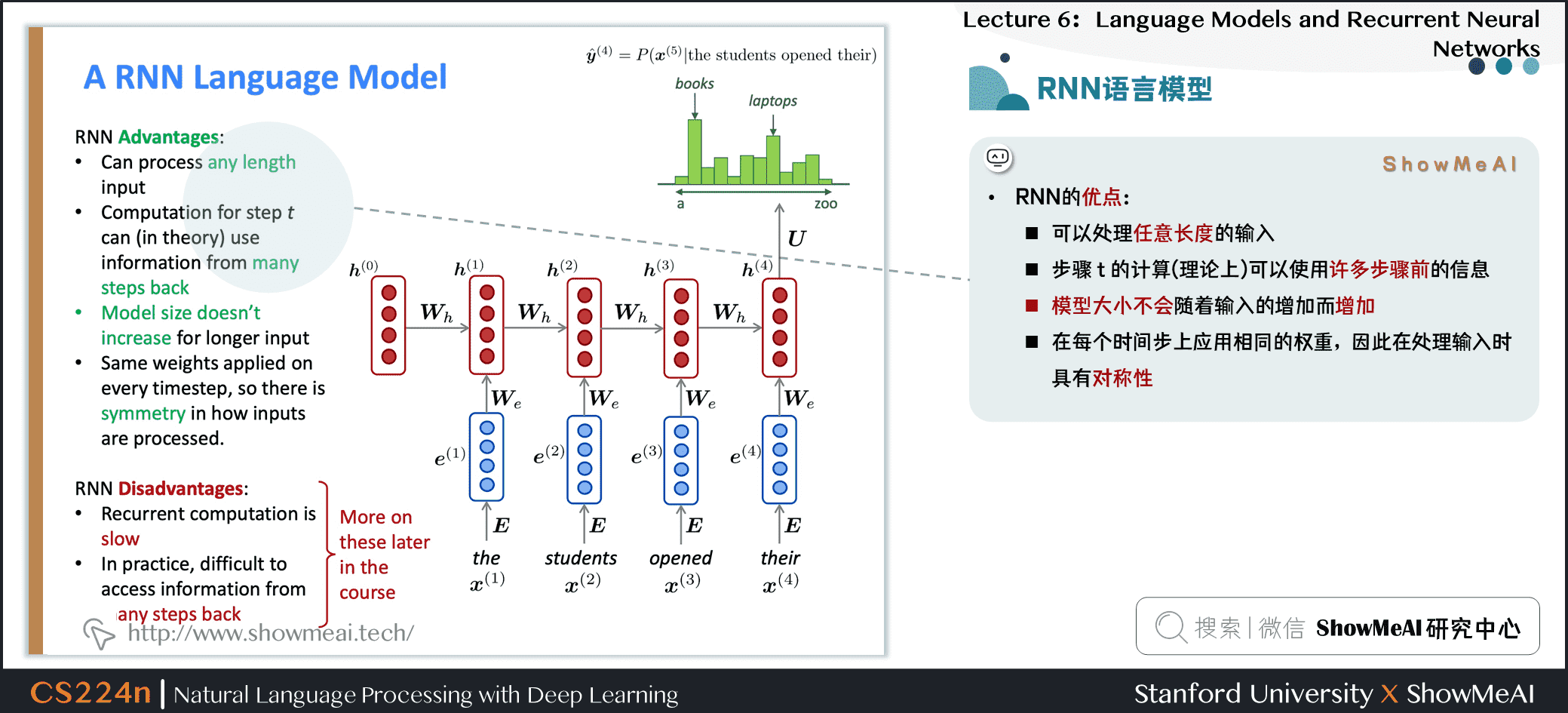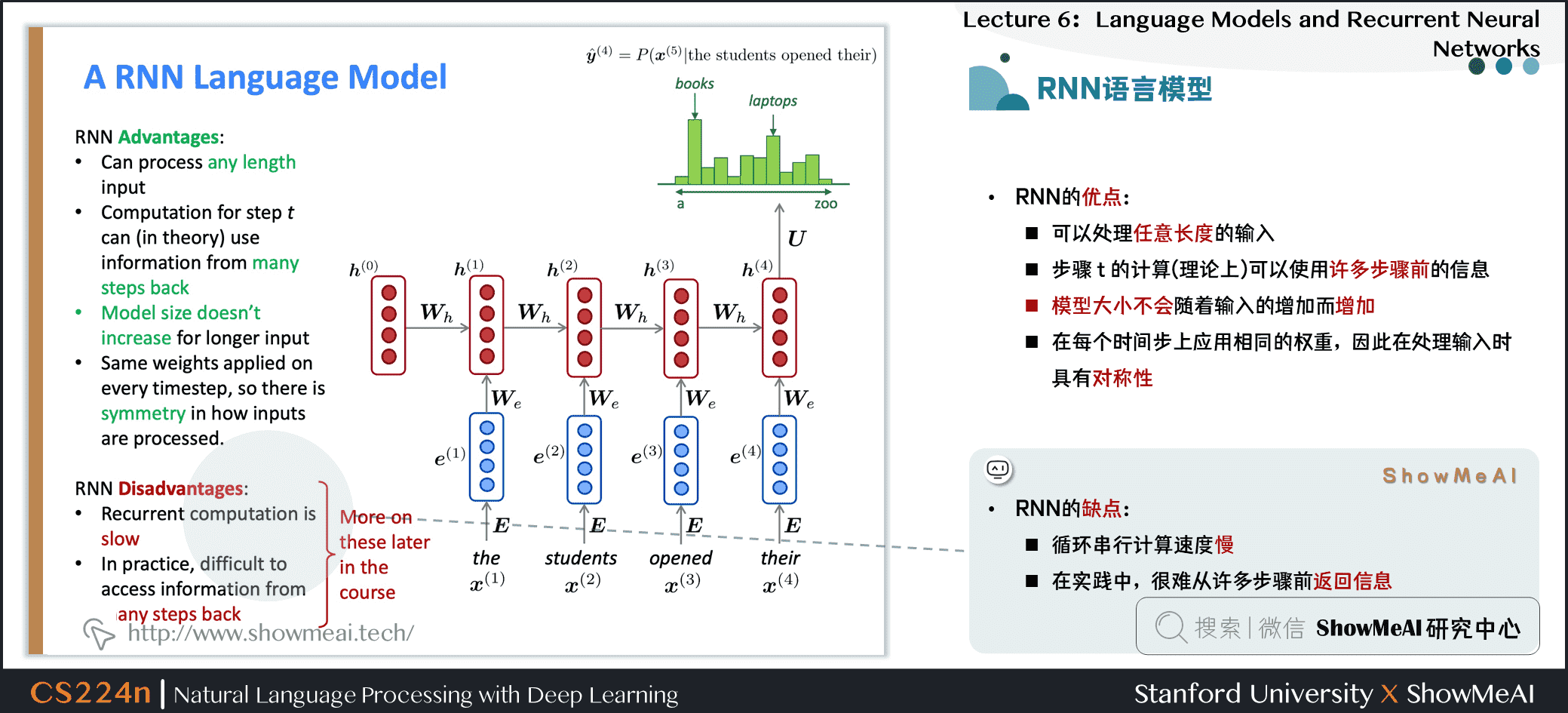
RNN的优点
- 可以处理任意长度的输入
- 步骤 \(t\) 的计算(理论上)可以使用许多步骤前的信息
- 模型大小不会随着输入的增加而增加
- 在每个时间步上应用相同的权重,因此在处理输入时具有对称性
RNN的缺点
- 循环串行计算速度慢
- 在实践中,很难从许多步骤前返回信息
2.4 训练一个RNN语言模型
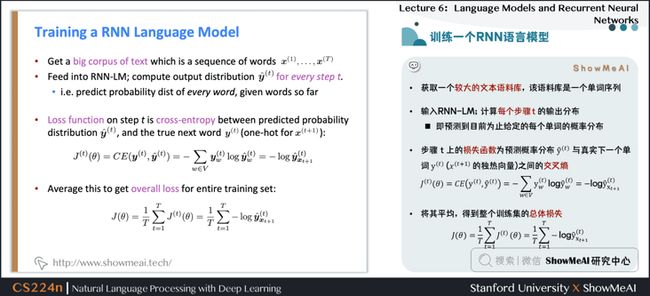
- 获取一个较大的文本语料库,该语料库是一个单词序列
输入RNN-LM;计算每个步骤 \(t\) 的输出分布
- 即预测到目前为止给定的每个单词的概率分布
- 步骤 \(t\) 上的损失函数为预测概率分布 \(\hat{\boldsymbol{y}}^{(t)}\) 与真实下一个单词\({\boldsymbol{y}}^{(t)}\) (\(x^{(t+1)}\)的独热向量)之间的交叉熵
$$ J^{(t)}(\theta)=C E\left(\boldsymbol{y}^{(t)}, \hat{\boldsymbol{y}}^{(t)}\right)=-\sum_{w \in V} \boldsymbol{y}_{w}^{(t)} \log \hat{\boldsymbol{y}}_{w}^{(t)}=-\log \hat{\boldsymbol{y}}_{\boldsymbol{x}_{t+1}}^{(t)} $$
- 将其平均,得到整个训练集的总体损失
$$ J(\theta)=\frac{1}{T} \sum_{t=1}^{T} J^{(t)}(\theta)=\frac{1}{T} \sum_{t=1}^{T}-\log \hat{\boldsymbol{y}}_{\boldsymbol{x}_{t+1}}^{(t)} $$
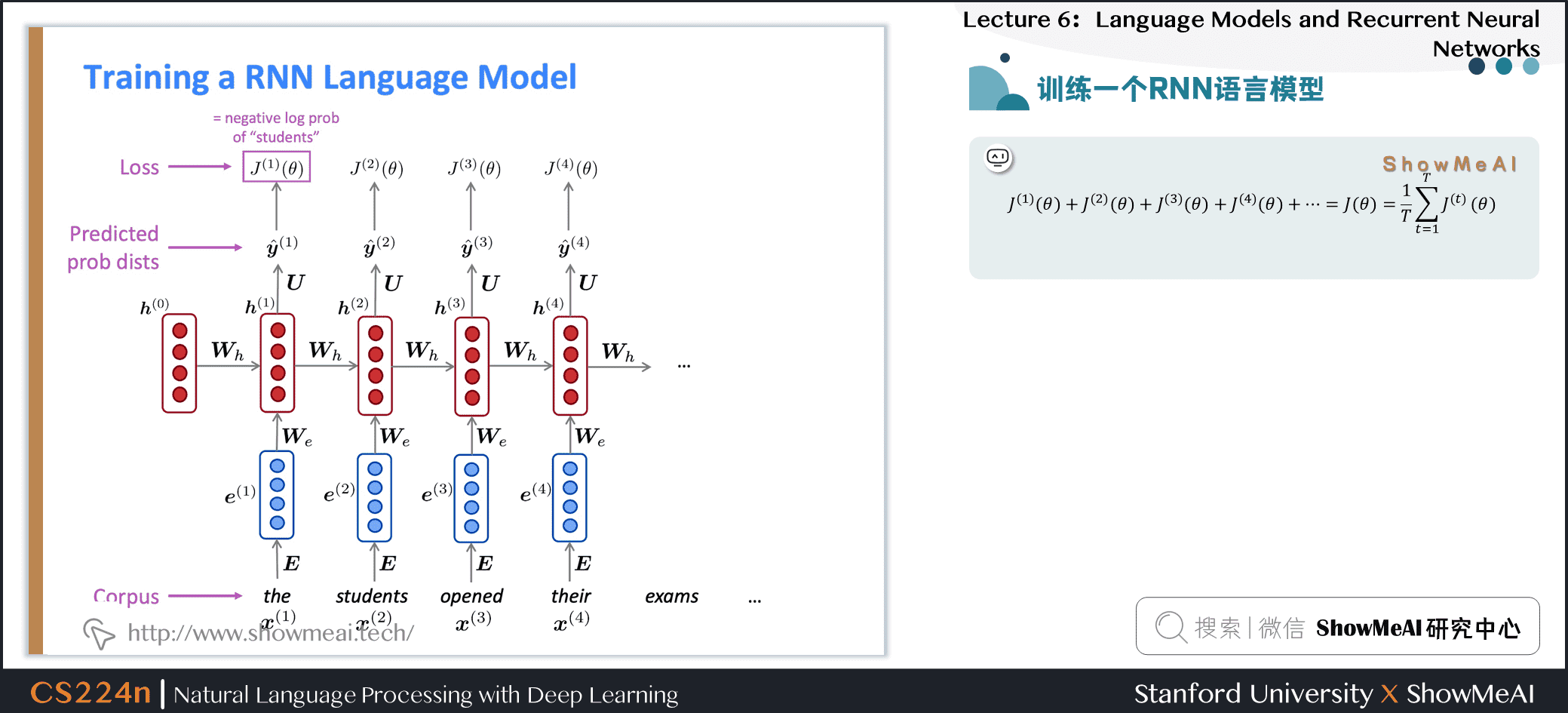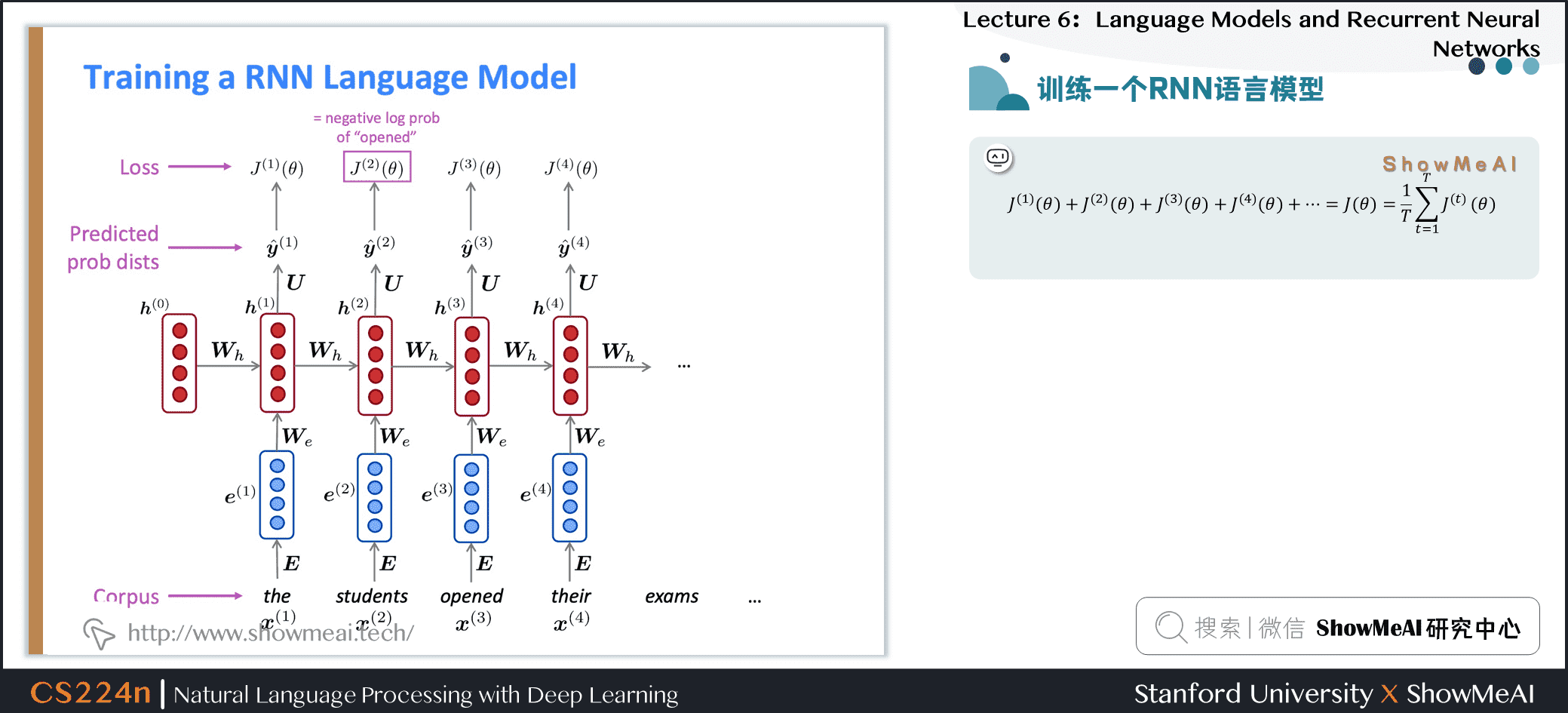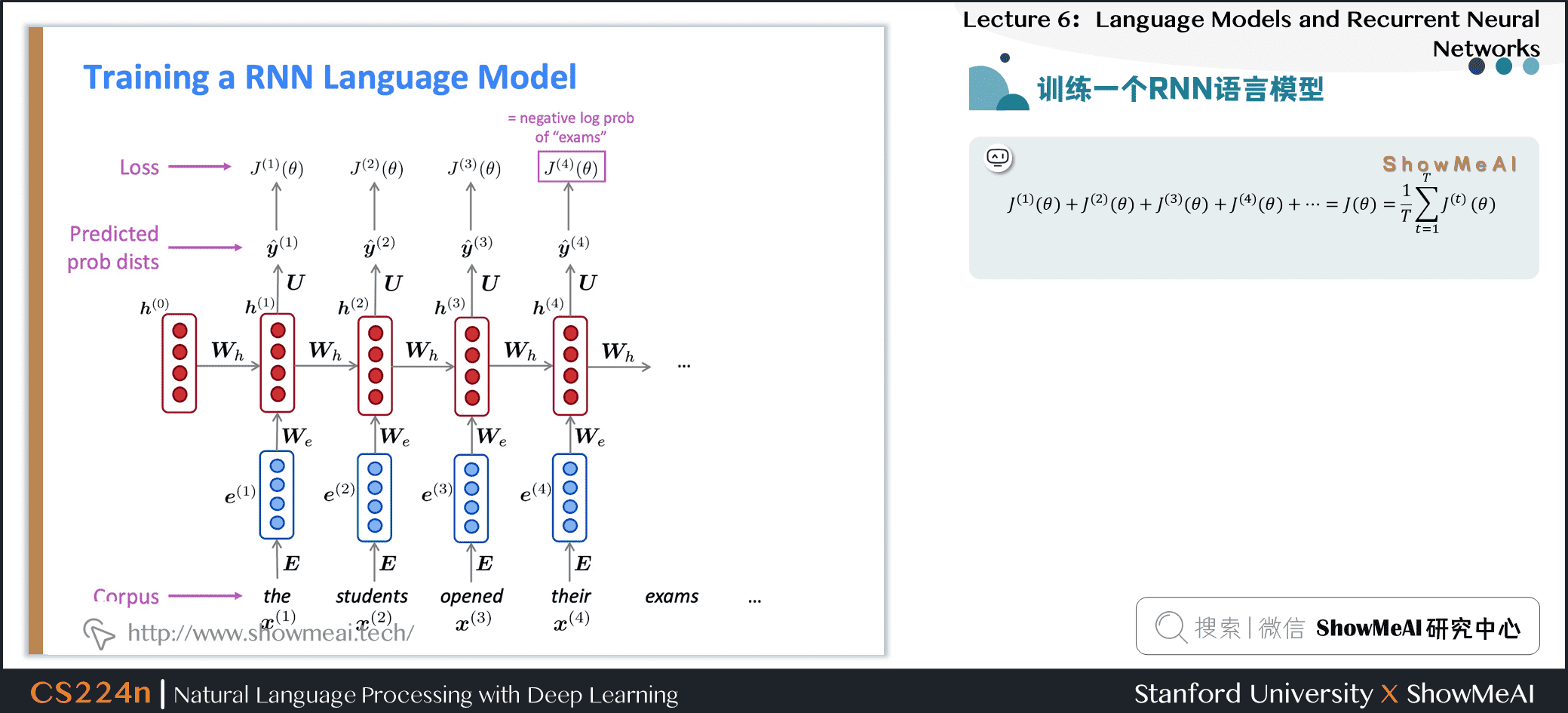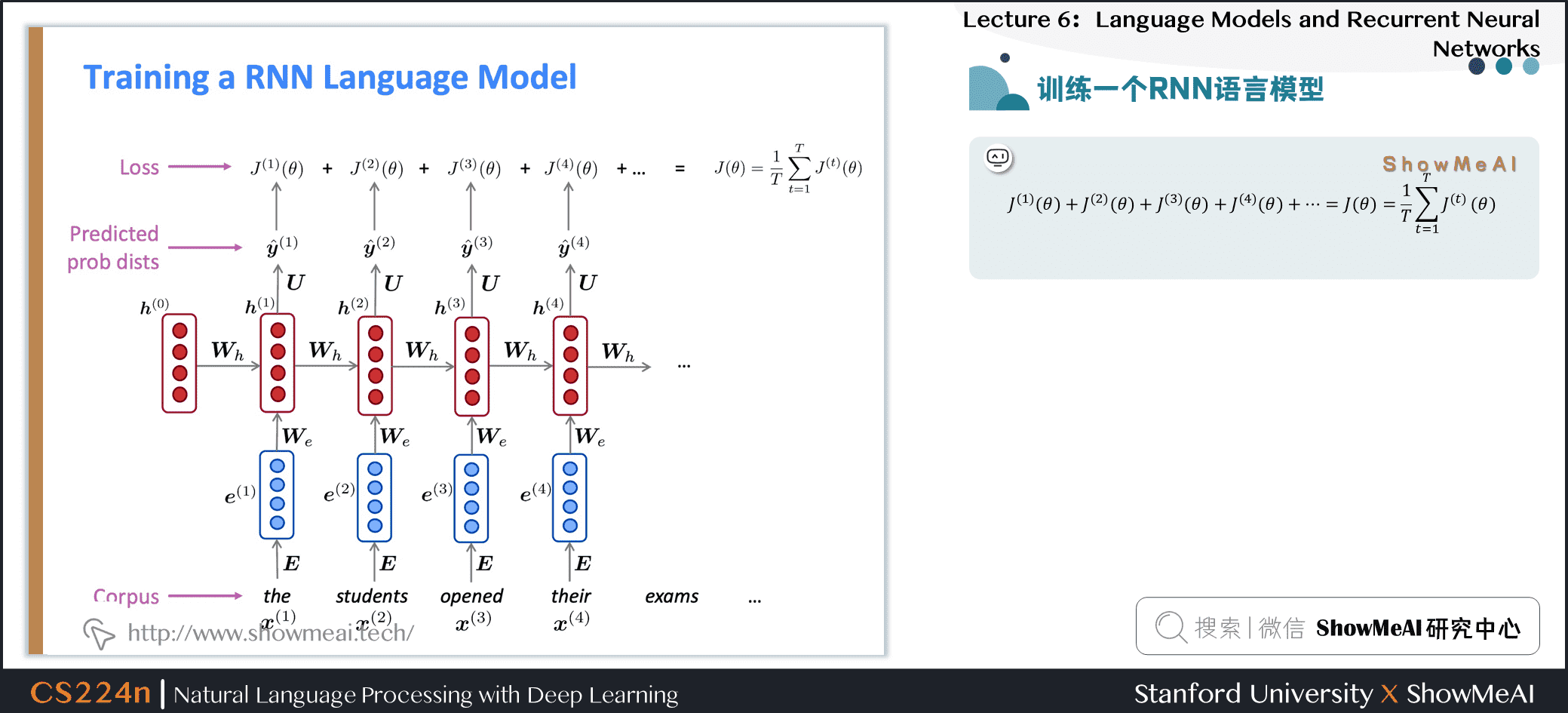
2.5 训练一个RNN语言模型
$$ J^{(1)}(\theta)+J^{(2)}(\theta)+J^{(3)}(\theta)+J^{(4)}(\theta)+\cdots=J(\theta)=\frac{1}{T} \sum_{t=1}^{T} J^{(t)}(\theta) $$
2.6 训练一个RNN语言模型
- 然而:计算整个语料库 \(\boldsymbol{x}^{(1)}, \ldots, \boldsymbol{x}^{(T)}\) 的损失和梯度太昂贵了
$$ J(\theta)=\frac{1}{T} \sum_{t=1}^{T} J^{(t)}(\theta) $$
- 在实践中,我们通常将 \(\boldsymbol{x}^{(1)}, \ldots, \boldsymbol{x}^{(T)}\) 看做一个句子或是文档
- 回忆:随机梯度下降允许我们计算小块数据的损失和梯度,并进行更新
- 计算一个句子的损失 \(J(\theta)\) (实际上是一批句子),计算梯度和更新权重。重复上述操作。
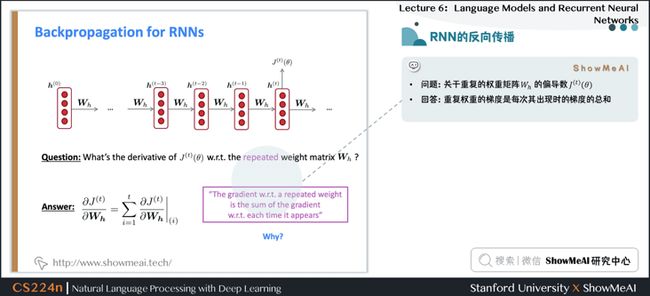
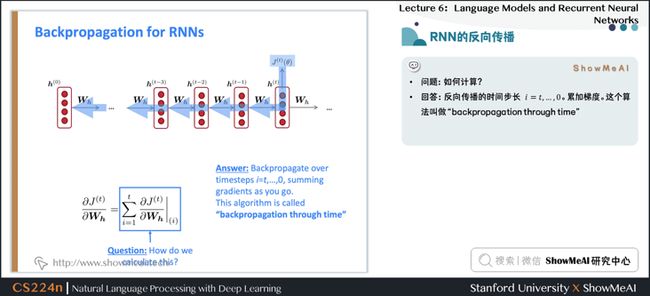
2.7 RNN的反向传播
- 问题:关于 重复的 权重矩阵 \(W_h\) 的偏导数 \(J^{(t)}(\theta)\)
- 回答:重复权重的梯度是每次其出现时的梯度的总和
$$ \frac{\partial J^{(t)}}{\partial \boldsymbol{W}_{\boldsymbol{h}}}=\sum_{i=1}^{t}\left.\frac{\partial J^{(t)}}{\partial \boldsymbol{W}_{\boldsymbol{h}}}\right|_{(i)} $$
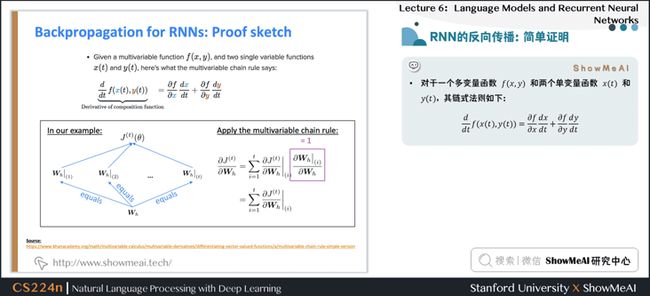
2.8 多变量链式法则
Source: https://www.khanacademy.org/m...
- 对于一个多变量函数 \(f(x,y)\) 和两个单变量函数 \(x(t)\) 和 \(y(t)\),其链式法则如下:
$$ \frac{d}{d t} f(x(t), y(t))=\frac{\partial f}{\partial x} \frac{d x}{d t}+\frac{\partial f}{\partial y} \frac{d y}{d t} $$
2.9 RNN的反向传播:简单证明
- 对于一个多变量函数 \(f(x,y)\) 和两个单变量函数 \(x(t)\) 和 \(y(t)\),其链式法则如下:
$$ \frac{d}{d t} f(x(t), y(t))=\frac{\partial f}{\partial x} \frac{d x}{d t}+\frac{\partial f}{\partial y} \frac{d y}{d t} $$
2.10 RNN的反向传播
- 问题:如何计算?
- 回答:反向传播的时间步长 \(i=t,\dots,0\)。累加梯度。这个算法叫做 “backpropagation through time”
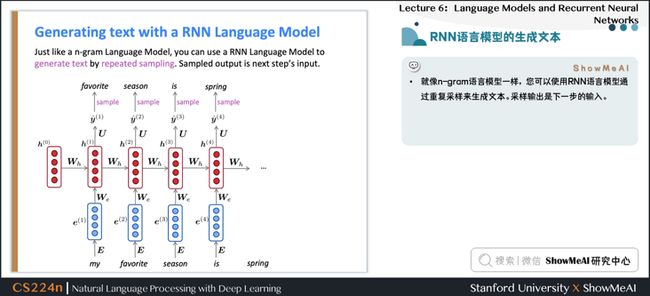
2.11 RNN语言模型的生成文本
- 就像n-gram语言模型一样,你可以使用RNN语言模型通过重复采样来生成文本。采样输出是下一步的输入。
2.12 RNN语言模型的生成文本
Source: https://medium.com/@samim/oba...
Source: https://medium.com/deep-writi...
Source: https://gist.github.com/nylki...
Source: http://aiweirdness.com/post/1...
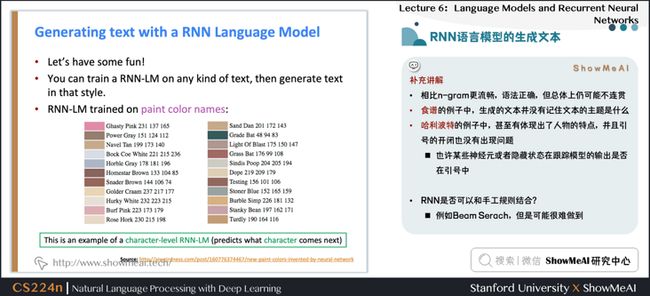
补充讲解
- 相比n-gram更流畅,语法正确,但总体上仍然很不连贯
- 食谱的例子中,生成的文本并没有记住文本的主题是什么
哈利波特的例子中,甚至有体现出了人物的特点,并且引号的开闭也没有出现问题
- 也许某些神经元或者隐藏状态在跟踪模型的输出是否在引号中
RNN是否可以和手工规则结合?
- 例如Beam Serach,但是可能很难做到
3.评估语言模型
3.1 评估语言模型
- 标准语言模型评估指标是 perplexity 困惑度
- 这等于交叉熵损失 \(J(\theta)\) 的指数
$$ =\prod_{t=1}^{T}\left(\frac{1}{\hat{y}_{x_{t+1}}^{(t)}}\right)^{1 / T}=\exp \left(\frac{1}{T} \sum_{t=1}^{T}-\log \hat{\boldsymbol{y}}_{\boldsymbol{x}_{t+1}}^{(t)}\right)=\exp (J(\theta)) $$
- 困惑度越低效果越好
3.2 RNN极大地改善了困惑度
Source: https://research.fb.com/build...
3.3 为什么我们要关心语言模型?
语言模型是一项基准测试任务,它帮助我们衡量我们在理解语言方面的 进展
- 生成下一个单词,需要语法,句法,逻辑,推理,现实世界的知识等
语言建模是许多NLP任务的子组件,尤其是那些涉及生成文本或估计文本概率的任务
- 预测性打字、语音识别、手写识别、拼写/语法纠正、作者识别、机器翻译、摘要、对话等等
3.4 要点回顾
- 语言模型:预测下一个单词的系统
循环神经网络:一系列神经网络
- 采用任意长度的顺序输入
- 在每一步上应用相同的权重
- 可以选择在每一步上生成输出
- 循环神经网络 \(\ne\) 语言模型
- 我们已经证明,RNNs是构建LM的一个很好的方法。
- 但RNNs的用处要大得多!
3.5 RNN可用于句子分类
- 如何计算句子编码
- 基础方式:使用最终隐层状态
- 通常更好的方式:使用所有隐层状态的逐元素最值或均值
- Encoder的结构在NLP中非常常见
3.6 RNN语言模型可用于生成文本
- 这是一个条件语言模型的示例。我们使用语言模型组件,并且最关键的是,我们根据条件来调整它
4.视频教程
可以点击 B站 查看视频的【双语字幕】版本
https://www.bilibili.com/vide...
5.参考资料
- 本讲带学的在线阅翻页本
- 《斯坦福CS224n深度学习与自然语言处理》课程学习指南
- 《斯坦福CS224n深度学习与自然语言处理》课程大作业解析
- 【双语字幕视频】斯坦福CS224n | 深度学习与自然语言处理(2019·全20讲)
- Stanford官网 | CS224n: Natural Language Processing with Deep Learning
ShowMeAI 系列教程推荐
- 大厂技术实现 | 推荐与广告计算解决方案
- 大厂技术实现 | 计算机视觉解决方案
- 大厂技术实现 | 自然语言处理行业解决方案
- 图解Python编程:从入门到精通系列教程
- 图解数据分析:从入门到精通系列教程
- 图解AI数学基础:从入门到精通系列教程
- 图解大数据技术:从入门到精通系列教程
- 图解机器学习算法:从入门到精通系列教程
- 机器学习实战:手把手教你玩转机器学习系列
- 深度学习教程 | 吴恩达专项课程 · 全套笔记解读
- 自然语言处理教程 | 斯坦福CS224n课程 · 课程带学与全套笔记解读
自然语言处理 (NLP) 教程
- NLP教程(1)- 词向量、SVD分解与Word2vec
- NLP教程(2)- GloVe及词向量的训练与评估
- NLP教程(3)- 神经网络与反向传播
- NLP教程(4)- 句法分析与依存解析
- NLP教程(5)- 语言模型、RNN、GRU与LSTM
- NLP教程(6)- 神经机器翻译、seq2seq与注意力机制
- NLP教程(7)- 问答系统
- NLP教程(8)- NLP中的卷积神经网络
- NLP教程(9)- 句法分析与树形递归神经网络
斯坦福 CS224n 课程带学详解
- 斯坦福NLP课程 | 第1讲 - NLP介绍与词向量初步
- 斯坦福NLP课程 | 第2讲 - 词向量进阶
- 斯坦福NLP课程 | 第3讲 - 神经网络知识回顾
- 斯坦福NLP课程 | 第4讲 - 神经网络反向传播与计算图
- 斯坦福NLP课程 | 第5讲 - 句法分析与依存解析
- 斯坦福NLP课程 | 第6讲 - 循环神经网络与语言模型
- 斯坦福NLP课程 | 第7讲 - 梯度消失问题与RNN变种
- 斯坦福NLP课程 | 第8讲 - 机器翻译、seq2seq与注意力机制
- 斯坦福NLP课程 | 第9讲 - cs224n课程大项目实用技巧与经验
- 斯坦福NLP课程 | 第10讲 - NLP中的问答系统
- 斯坦福NLP课程 | 第11讲 - NLP中的卷积神经网络
- 斯坦福NLP课程 | 第12讲 - 子词模型
- 斯坦福NLP课程 | 第13讲 - 基于上下文的表征与NLP预训练模型
- 斯坦福NLP课程 | 第14讲 - Transformers自注意力与生成模型
- 斯坦福NLP课程 | 第15讲 - NLP文本生成任务
- 斯坦福NLP课程 | 第16讲 - 指代消解问题与神经网络方法
- 斯坦福NLP课程 | 第17讲 - 多任务学习(以问答系统为例)
- 斯坦福NLP课程 | 第18讲 - 句法分析与树形递归神经网络
- 斯坦福NLP课程 | 第19讲 - AI安全偏见与公平
- 斯坦福NLP课程 | 第20讲 - NLP与深度学习的未来
![]()