Keras深度学习实战（6）——深度学习过拟合问题及解决方法

0. 前言

在《神经网络性能优化技术》中，我们经常看到这样的现象——模型的训练准确率约为 100％，而测试准确率约为 98％，这是在训练数据集上出现过拟合的情况。接下来，我们直观地了解训练与测试准确率之间的差异的原因以及解决方法。

1. 过拟合问题介绍

过拟合是在训练数据上能够获得很好的性能， 但是在训练数据外的数据集上却不能很好地拟合数据。为了了解导致过拟合的现象，对比两种情况，在这些情况下比较训练和测试的准确性以及权重的直方图：

• 模型运行 5 个 epoch
• 模型运行 100 个 epoch

两个模型的架构完全相同，不同之处仅在于使用不同的 epoch：

# 模型 1 运行 5 个 epoch
model_1 = Sequential()
model_1.add(Dense(1000, input_dim=num_pixels, activation='relu'))
model_1.add(Dense(num_classes, activation='softmax'))
model_1.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['acc'])
history = model_1.fit(x_train, y_train,
                    validation_data=(x_test, y_test),
                    epochs=100,
                    batch_size=64,
                    verbose=1)
# 模型 2 运行 5 个 epoch
model_2 = Sequential()
model_2.add(Dense(1000, input_dim=num_pixels, activation='relu'))
model_2.add(Dense(num_classes, activation='softmax'))
model_2.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['acc'])
history = model_2.fit(x_train, y_train,
                    validation_data=(x_test, y_test),
                    epochs=100,
                    batch_size=64,
                    verbose=1)

两种情况之间的训练数据集和测试数据集之间的准确率比较结果如下：

Epoch数	训练集准确率	测试集准确率
5	97.65%	97.23%
100	100%	98.32%

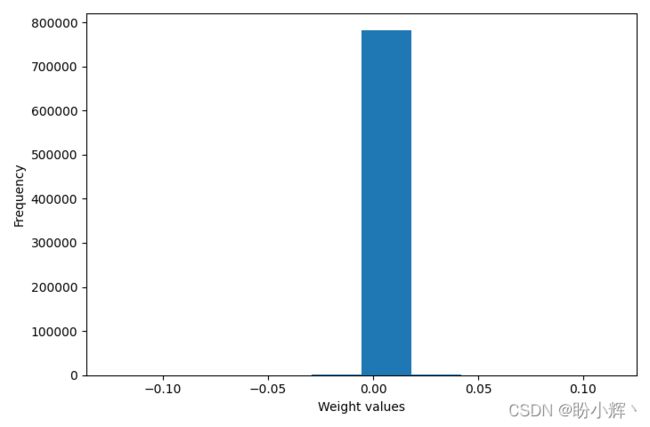
绘制权重直方图如下，与 5 个 epoch 相比，100 个 epoch 的权重分布更广：

plt.subplot(211)
plt.hist(model.get_weights()[0].flatten())
plt.title('Histogram of weight values in 5 epochs')
plt.xlabel('Weight values')
plt.ylabel('Frequency')
plt.subplot(212)
plt.hist(model.get_weights()[0].flatten())
plt.title('Histogram of weight values in 100 epochs')
plt.xlabel('Weight values')
plt.ylabel('Frequency')
plt.show()

从前面的图片中，可以看到，与训练 5 个 epoch 的模型相比，训练 100 个 epoch 的模型权重值分散度更高。这是因为与运行 5 个 epoch 时相比，当模型运行 100 个 epoch 时，该模型在训练数据集上过拟合的机会更大，其会针对离群值进行调整。
过拟合的模型更有可能具有更大/更小的权重值(权重值的分布范围更广)去拟合那些异常数据，因此有机会通过调整权重来解决过拟合。

2. 使用正则化解决过拟合问题

接下来，我们将研究解决过拟合问题的方法。我们已经确定了权重过大是过拟合的原因之一，因此我们首先想到的就是对高权重值进行惩罚。正则化会对模型中的较高的权重较高进行惩罚， L1 和 L2 正则化是最常用的正则化技术之一，其工作方式如下：

1. L2 正则化除了最小化损失函数(以下公式中的第一项，这里假设为平方损失的总和)之外，还使神经网络指定层的权重平方的加权总和(以下公式的第二项)最小化：

$$\mathcal{L}=\sum (y-\bar{y}{)}^2+\lambda \sum w_i^2$$

其中，$\lambda$ 是与正则化项相关联的权重，是一个权衡两项损失重要性的超参数，$y$ 是真实值，$\bar{y}$ 是预测值，$w_i$ 是模型中的权重值。

2. L1 正则化除了最小化损失函数(以下公式中的第一项，这里假设为平方损失的总和)之外，还使神经网络指定层的权重绝对值的加权总和(以下公式的第二项)最小化：

$$\mathcal{L}=\sum (y-\bar{y}{)}^2+\lambda \sum |w_i|$$

这样，我们就确保模型不会仅针对训练数据集中的极端/异常情况微调权重。模型中使用 L1/L2 正则化在 Keras 中实现，如下所示：

from keras.regularizers import l2

model = Sequential()
model.add(Dense(1000, input_dim=num_pixels, activation='relu', kernel_regularizer=l2(0.1)))
model.add(Dense(num_classes, activation='softmax', kernel_regularizer=l2(0.1)))
model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['acc'])

history = model.fit(x_train, y_train,
                    validation_data=(x_test, y_test),
                    epochs=100,
                    batch_size=64,
                    verbose=1)

以上代码调用了 Dense 层附加参数 kernel_regularizer，用于使用指定正则化方法，本例中使用 L2 正则化，并指定正则化权重的 $\lambda$ 值为 0.1：

kernel_regularizer=l2(0.1)

在进行正则化后，训练数据集的准确率并未达到 100％，而测试数据的准确性同样可以达到 98％。将输入层链接到隐藏层的权重提取如下：

model.get_weights()[0].flatten()

提取权重后，将按以下方式绘制权重：

plt.hist(model.get_weights()[0].flatten())

L2 正则化后的权重直方图如下所示：

与之前的情况相比，现在大多数权重都接近于 0，因此避免过拟合问题的出现。在 L1 正则化的情况下，我们也可以看到类似的情况。与未进行正则化时的权重值相比，存在正则化时的权重值要低得多。因此，L1 和 L2 正则化有助于我们避免训练数据集上方的过拟合问题。

3. 使用 Dropout 解决过拟合问题

在使用正则化克服过拟合中，我们使用 L1/L2 正则化作为避免过拟合的一种方法。接下来，我们将使用另一个有助于实现相同目标的强大工具——Dropout。
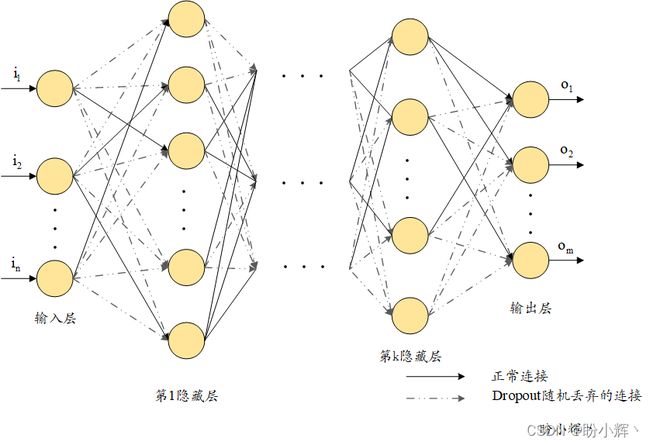
Dropout 可以认为是一种模型训练方法，其中每批数据训练时只有一定比例的权重被更新，而其余的权重不被更新。也就是说，在权重更新过程中并非所有权重都得到更新，避免了某些权重达到非常高的值：

from keras.layers import Dropout

model = Sequential()
model.add(Dense(1000, input_dim=num_pixels, activation='relu'))
model.add(Dropout(0.75))
model.add(Dense(num_classes, activation='softmax'))
model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['acc'])

history = model.fit(x_train, y_train,
                    validation_data=(x_test, y_test),
                    epochs=50,
                    batch_size=64,
                    verbose=1)

在前面的代码中，我们给出了 0.75 的 Dropout 率；也就是说，在每次权重更新迭代中随机选择 75％ 的权重不会更新，或者可以理解为每次训练时网络间的每个连接有 75% 概率断开，从而减少了网络间的连接：

这可以令训练和测试准确率之间的差距低于没有 Dropout 时模型训练和测试准确率的差距。绘制隐藏层的权重直方图：

plt.hist(model.get_weights()[0].flatten())

小结

本节中，我们介绍了过拟合问题出现原因以及解决过拟合的常用的几种解决方法，除此之外，我们已经讲解过的批归一化也是常用的解决过拟合的方法，在之后的学习中我们也会学习诸如数据集扩充等其它过拟合的解决方法。

系列链接

Keras深度学习实战（1）——神经网络基础与模型训练过程详解
Keras深度学习实战（2）——使用Keras构建神经网络
Keras深度学习实战（3）——神经网络性能优化技术
Keras深度学习实战（4）——深度学习中常用激活函数和损失函数详解
Keras深度学习实战（5）——批归一化详解