机器学习(18)——卷积神经网络(三)
前言
卷积神经网络发展非常迅速,应用非常广阔,所以近几年的卷积神经网络得到了长足的发展,下图为卷积神经网络近几年发展的大致轨迹。
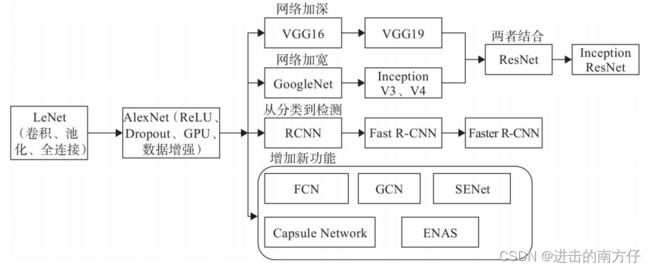
1998年LeCun提出了 LeNet,可谓是开山鼻祖,系统地提出了卷积层、 池化层、全连接层等概念。2012年Alex等提出 AlexNet,提出 一些训练深度网络的重要方法或技巧,如 Dropout、ReLu、GPU、数据增强方法等,随后各种各样的深度卷积神经网络模型相继被提出,其中比较有代表性的有 VGG 系列,GoogLeNet 系列,ResNet 系列,DenseNet 系列等,他们的网络层数整体趋势逐渐增多。以网络模型在 ILSVRC 挑战赛 ImageNet数据集上面的分类性能表现为例,如下图,在 AlexNet 出现之前的网络模型都是浅层的神经网络,Top-5(表示神经网络返回的前5个最大概率值代表的内容中有一个是正确的)错误率均在 25%以上,AlexNet 8 层的深层神经网络将 Top-5 错误率降低至 16.4%,性能提升巨大,后续的 VGG、GoogleNet 模型继续将错误率降低至 6.7%;ResNet 的出现首次将网络层数提升至 152 层,错误率也降低至 3.57%。

LeNet-5
LeNet 是Yann LeCun等人提出的卷积神经网络结构,用于解决手写数字识别的机器视觉任务。1989年。一般来说,LeNet 是指 LeNet-5,是一个简单的卷积神经网络。卷积神经网络是一种前馈神经网络,其人工神经元可以对覆盖范围内的一部分周围细胞做出反应,在大规模图像处理中表现良好。LeNet 作为早期卷积神经网络的代表,拥有卷积神经网络的基本单元,如卷积层、池化层和全连接层,为卷积神经网络的未来发展奠定了基础。
模型架构:LeNet-5 模型结构为 输入层-卷积层-池化层-卷积层-池化层-全连接层-全 连接层-输出,为串联模式。
- 每个卷积层包括三个部分:卷积、池化和非线性激活函数;
- 使用卷积提取空间特征;
- 采用降采样的平均池化层;
- 使用 tanh 激活函数;
- 使用 MLP 作为最后一个分类器;
- 层间稀疏连接,降低计算复杂度。
AlexNet
2012 年,ILSVRC12 挑战赛 ImageNet 数据集分类任务的冠军 Alex Krizhevsky 提出了 8
层的深度神经网络模型 AlexNet。AlexNet 在 ImageNet 取得了 15.3% 的 Top-5 错误率,比第二名在错误率上降低了 10.9%。原始论文的主要结果是模型的深度对其高性能至关重要,这在计算上是昂贵的,但由于在训练过程中使用了图形处理单元(GPU) 而变得可行。
模型架构:接收输入为 224 × 224 大小的彩色图片数据,经过五个卷积层和三个全连接层后得到样本属于 1000 个类别的概率分布。为了降低特征图的维度,AlexNet 在第 1、2、5 个卷积层后添加了 Max Pooling 层,网络的参数量达到了 6000 万个。为了能够在当时的显卡设备 NVIDIA GTX 580(3GB 显存)上训练模型,Alex Krizhevsky 将卷积层、前 2 个全连接层等拆开在两块显卡上面分别训练,最后一层合并到一张显卡上面,进行反向传播更新。
- 由 5 层卷积和 3 层全连接组成,输入图像为 3 通道 224×224 大小,网络规 模远大于 LeNet;
- 采用了 ReLU 激活函数,过去的神经网络大多采用 Sigmoid 激活函数,计算相对复杂,容易出现梯度弥散现象。
- 引入 Dropout 层。Dropout 提高了模型的泛化能力,防止过拟合,提升模型的鲁棒性。
- 具备一些很好的训练技巧,包括数据增广、学习率策略、Weight Decay 等。
VGG
AlexNet 模型的优越性能启发了业界朝着更深层的网络模型方向研究。2014 年,ILSVRC14 挑战赛 ImageNet 分类任务的亚军牛津大学 VGG 实验室提出了 VGG11、VGG13、VGG16、VGG19 等一系列的网络模型,如下图。VGG可以看成是加深版本的AlexNet,都是 Conv Layer + FC layer,VGG16 在 ImageNet 取得了 7.4%的 Top-5 错误率,比 AlexNet 在错误率上降低了 7.9%。
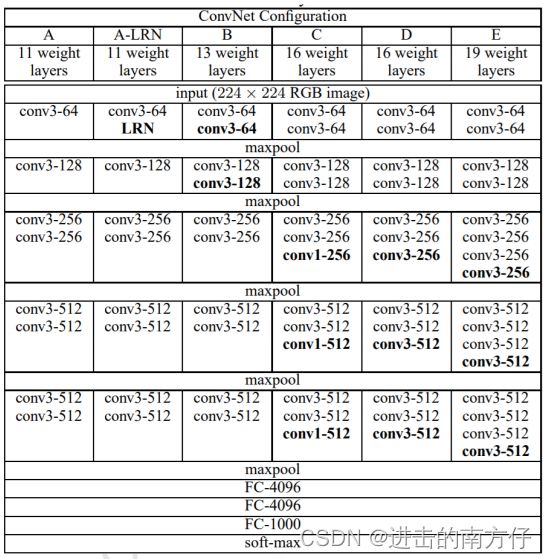
模型架构:以 VGG16 为例,它接受 224 × 224 大小的彩色图片数据,经过 2 个 Conv-Conv-Pooling 单元,和 3 个 Conv-Conv-Conv-Pooling 单元的堆叠,最后通过 3 层全连接层输出当前图片分别属于 1000 类别的概率分布。
- 更深的网络结构:网络层数由 AlexNet 的 8 层增至 16 和 19 层,更深的网络意味着更强大的网络能力,也意味着需要更强大的计算力,不过后来硬件发展也很快,显卡运算力也在快速增长,以此助推深度学习的快速发展。
- 全部采用更小的 3 × 3 卷积核,相对于 AlexNet 中 7 × 7 的卷积核,参数量更少,计算代价更低。
- 采用更小的池化层 2 × 2 窗口和步长 s = 2 \boldsymbol{s = 2} s=2,而 AlexNet 中是步长 = 2 、 3 × 3 \boldsymbol{ = 2、3 × 3} s=2、3×3 的池化窗口。
GoogleNet
在介绍 GoogleNet 之前,我们需要对卷积核进行讨论。再前面说过 VGG 模型使用的卷积核大小均是 3 × 3,参数量更少,计算代价更低,同时因为两个 3 × 3 卷积核的感受野相当于一个 5 × 5 卷积核,能捕获图像更多的细节信息,因此 3 × 3 卷积核在性能表现上更优越。因此业界开始探索卷积核最小的情况:1 × 1 卷积核。

上图中,输入为 3 通道的 5 × 5 图片,与单个 1 × 1 的卷积核进行卷积运算,每个通道的数据与对应通道的卷积核运算,得到 3 个通道的中间矩阵,对应位置相加得到最终的输出张量。对于输入 shape 为 [ b , h , w , c i n ] \boldsymbol{[b, h,w,c_{in}]} [b,h,w,cin],1 × 1 卷积层的输出为 [ b , h , w , c o u t ] \boldsymbol{[b, h,w,c_{out}]} [b,h,w,cout],其中 c i n \boldsymbol{c_{in}} cin 为输入数据的通道数, c o u t \boldsymbol{c_{out}} cout 为输出数据的通道数,也是 1 × 1 卷积核的数量。 1 × 1 卷积核的一个特别之处在于,它可以不改变特征图的宽高,而只对通道数 c \boldsymbol{c} c 进行变换。这起到了降维的作用,因此 1 × 1 卷积核可以帮助我们降低参数数量。
2014 年,ILSVRC14 挑战赛的冠军 Google 提出了大量采用 3 × 3 和1 × 1 卷积核的网络模型:GoogLeNet,网络层数达到了 22 层。虽然 GoogLeNet 的层数远大于 AlexNet,但是它的参数量却只有 AlexNet 的 1 12 \boldsymbol{\frac{1}{12}} 121,同时性能也远好于 AlexNet。在 ImageNet 数据集分类任务上,GoogLeNet 取得了 6.7%的 Top-5 错误率,比 VGG16 在错误率上降低了 0.7%。
模型架构:VGG 是增加网络的深度,但深度达到一个程度时,可能就成为瓶颈。 GoogLeNet 则从另一个维度来增加网络能力,每单元有许多层并行计算,让网络更宽了。GoogLeNet 网络通过大量堆叠 Inception 模块,形成了复杂的网络结构,如下图。
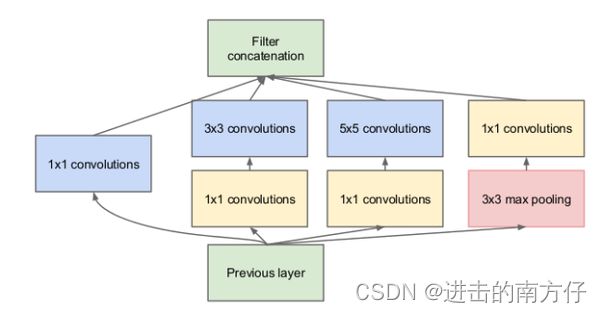
上图中,Inception 模块的输入为 X \boldsymbol{X} X,通过 4 个子网络得到 4 个网络输出,在通道轴上面进行拼接合并,形成 Inception 模块的输出。这 4 个子网络为:
- 1 × 1 卷积层;
- 1 × 1 卷积层,再通过一个 3 × 3 卷积层;
- 1 × 1 卷积层,再通过一个 5 × 5 卷积层;
- 3 × 3 最大池化层,再通过 1 × 1 卷积层。
GoogLeNet 的网络结构如下图所示,其中红色框中的网络结构即为 Inception 模块的网络结构。
- 引入 Inception 结构,这是一种网中网(Network In Network)的结构。通过网络的水平排布,可以用较浅的网络得到较好的模型能力,并进行多特征融合,同时更容易训练。使用了 1 × 1 卷积来先对特征通道进行降维,减少计算量。GoogLeNet 就是一个精心设计的性能良好的 Inception 网络(Inception v1)的 实例,即 GoogLeNet 是 Inception v1 网络的一种。
- 采用全局平均池化层。将后面的全连接层全部替换为简单的全局平均池化,在最后参数会变得更少。而在 AlexNet 中最后 3 层的全连接层参数差不多占总参数的 90%,使用大网络在宽度和深度上允许 GoogleNet 移除全连接层,但并不会影响到结果的精度。
ResNet
AlexNet、VGG、GoogLeNet 等网络模型的出现将神经网络的发展带入了几十层的阶段,研究人员发现网络的层数越深,越有可能获得更好的泛化能力。但是当模型加深以后,网络变得越来越难训练,这主要是由于梯度弥散和梯度爆炸现象造成的。在较深层数的神经网络中,梯度信息由网络的末层逐层传向网络的首层时,传递的过程中会出现梯度接近于 0 或梯度值非常大的现象。网络层数越深,这种现象可能会越严重。对于深层神经网络的梯度弥散和梯度爆炸现象,我们可以想到浅层神经网络不容易出现这些梯度现象,那么可以尝试给深层神经网络添加一种回退到浅层神经网络的机制。当深层神经网络可以轻松地回退到浅层神经网络时,深层神经网络可以获得与浅层神经网络相当的模型性能,而不至于更糟糕。
2015 年,微软亚洲研究院何凯明等人发表了深度残差网络(Residual Neural Network,简称 ResNet)算法 [10],并提出了 18 层、34 层、50 层、101层、152 层的 ResNet-18、ResNet-34、ResNet-50、ResNet-101 和 ResNet-152 等模型。ResNet 在网络结构上做了一大创新,即采用残差网络结构,而不再是简单地堆积层数,ResNet 在卷积神经网络中提供了一个新思路。ResNet 在 ILSVRC 2015 挑战赛 ImageNet数据集上的分类、检测等任务上面均获得了最好性能。
原理
ResNet 通过在卷积层的输入和输出之间添加残差链接实现层数回退机制。
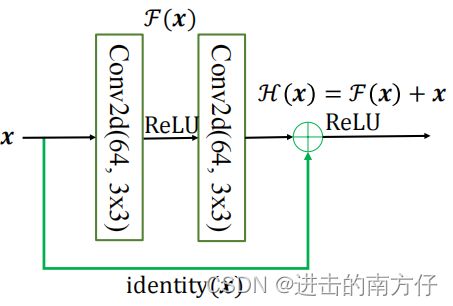
上图中,输入 x \boldsymbol{x} x 通过两个卷积层,得到特征变换后的输出 F ( ) \boldsymbol{F()} F(x),与输入 x \boldsymbol{x} x 进行对应元素的相加运算,得到最终输出 H ( x ) \boldsymbol{H(x)} H(x):
H ( x ) = F ( x ) + x \boldsymbol{H(x) = F(x) + x} H(x)=F(x)+x
H ( x ) \boldsymbol{H(x)} H(x) 叫作残差模块(Residual Block,简称 ResBlock),由于卷积神经网络需要学习映射 F ( x ) = H ( x ) − x \boldsymbol{F(x) = H(x) - x} F(x)=H(x)−x,故称为残差网络。为了能够满足输入 x \boldsymbol{x} x 与卷积层的输出出 F ( ) \boldsymbol{F()} F(x) 能够相加运算,需要输入 x \boldsymbol{x} x 的 shape 与 F ( ) \boldsymbol{F()} F(x) 的完全一致。当出现 shape 不一致时,一般通过在残差连接上添加额外的卷积运算环节将输入 x \boldsymbol{x} x 变换到与 F ( ) \boldsymbol{F()} F(x) 相同的 shape,如上图中 d e n t i t y ( ) \boldsymbol{dentity()} dentity(x) 函数。因为再卷积过程中我们常常使用 Vaild卷积,因此 d e n t i t y ( ) \boldsymbol{dentity()} dentity(x) 以1 × 1的卷积运算居多,主要用于调整输入的通道数。
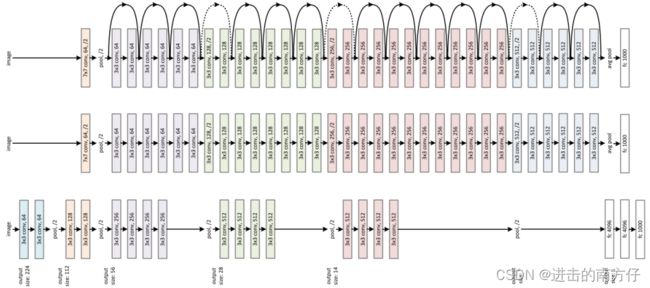
模型架构:34 层的深度残差网络、34 层的普通深度网络以及 19 层的 VGG 网络结构如下图。可以看到,深度残差网络通过堆叠残差模块,达到了较深的网络层数,从而获得了训练稳定、性能优越的深层网络模型。
- 层数非常深,已经超过百层;
- 引入残差单元来解决退化问题。
DenseNet
DenseNet 将前面所有层的特征图信息通过 Skip Connection 与当前层输出进行聚合,与 ResNet 的对应位置相加方式不同,DenseNet 采用在通道轴 c \boldsymbol{c} c 维度进行拼接操作,聚合特征信息。
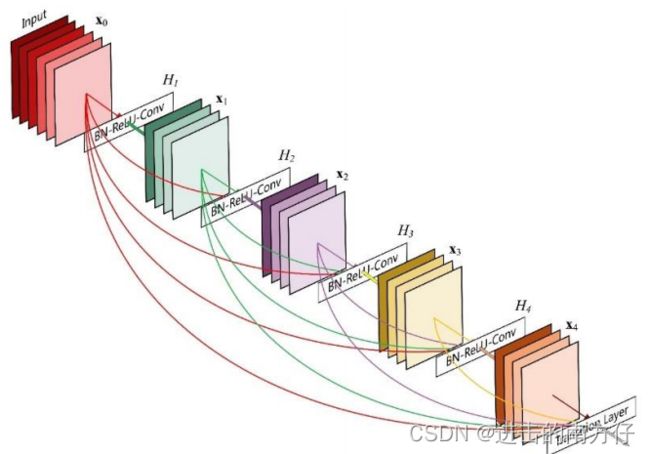
上图中,输入 X \boldsymbol{X} X 通过 H 1 \boldsymbol{H_1} H1 卷积层得到输出 X 1 \boldsymbol{X_1} X1, X 1 \boldsymbol{X_1} X1 与 X \boldsymbol{X} X 在通道轴上进行拼接,得到聚合后的特征张量,送入 H 2 \boldsymbol{H_2} H2 卷积层,得到输出 X 2 \boldsymbol{X_2} X2,同样的方法, X 2 \boldsymbol{X_2} X2 与前面所有层的特征信息 X 1 \boldsymbol{X_1} X1 与 X \boldsymbol{X} X 进行聚合,再送入下一层。如此循环,直至最后一层的输出 X 4 \boldsymbol{X_4} X4 和前面所有层的特征信息: { X i } i = 0 , 1 , 2 , 3 \boldsymbol{\{X_i\}_{i = 0, 1, 2 ,3}} {Xi}i=0,1,2,3进行聚合得到模块的最终输出。
模型架构:DenseNet 通过堆叠多个 Dense Block 构成复杂的深层神经网络。
- 引入来稠密连接模块解决退化问题。
不同版本的 DenseNet 的性能、DenseNet 与 ResNet 的性能比较,以及DenseNet 与 ResNet 训练曲线比较如下:
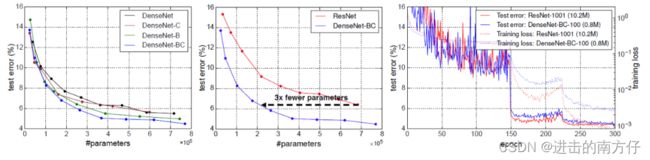
上一篇:卷积神经网络之池化层、BN 层