详解Java中KMP算法的图解与实现

目录

• 图解
• 代码实现

图解

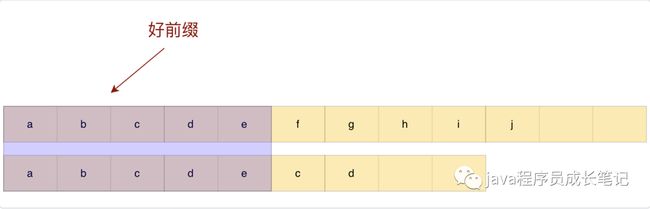
kmp算法跟之前讲的bm算法思想有一定的相似性。之前提到过，bm算法中有个好后缀的概念，而在kmp中有个好前缀的概念，什么是好前缀，我们先来看下面这个例子。

观察上面这个例子，已经匹配的abcde称为好前缀，a与之后的bcde都不匹配，所以没有必要再比一次，直接滑动到e之后即可。

那如果好前缀中有互相匹配的字符呢？

观察上面这个例子，这个时候如果我们直接滑到好前缀之后，则会过度滑动，错失匹配子串。那我们如何根据好前缀来进行合理滑动？

其实就是看当前的好前缀的前缀和后缀是否有匹配的，找到最长匹配长度，直接滑动。鉴于不止一次找最长匹配长度，我们完全可以先初始化一个数组，保存在当前好前缀情况下，最长匹配长度是多少，这时候我们的next数组就出来了。

我们定义一个next数组，表示在当前好前缀下，好前缀的前缀和后缀的最长匹配子串长度，这个最长匹配长度表示这个子串之前已经匹配过匹配了，不需要再次进行匹配，直接从子串的下一个字符开始匹配。

我们是否每次算next[i]时都需要每一个字符进行匹配，是否可以根据next[i - 1]进行推导以便减少不必要的比较。

带着这个思路我们来看看下面的步骤：

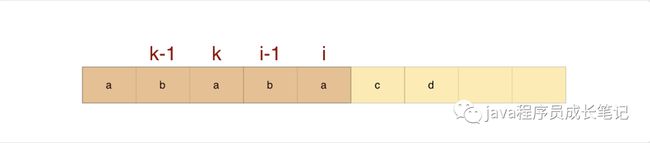
假设next[i - 1] = k - 1;

如果modelStr[k] = modelStr[i] 则next[i]=k

如果modelStr[k] != modelStr[i]，我们是否可以直接认定next[i] = next[i - 1]？

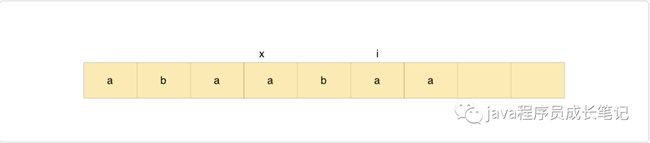
通过上面这个例子，我们可以很清晰的看到，next[i]!=next[i-1]，那当modelStr[k]!=modelStr[i]时候，我们已知next[0],next[1]…next[i-1]，如何推倒出next[i]呢？

假设modelStr[x…i]是前缀后缀能匹配的最长后缀子串，那么最长匹配前缀子串为modelStr[0…i-x]

我们在求这个最长匹配串的时候，他的前面的次长匹配串（不包含当前i的），也就是modelStr[x…i-1]在之前应该是已经求解出来了的，因此我们只需要找到这个某一个已经求解的匹配串，假设前缀子串为modelStr[0…i-x-1],后缀子串为modelStr[x…i-1],且modelStr[i-x] == modelStr[i],这个前缀后缀子串即为次前缀子串，加上当前字符即为最长匹配前缀后缀子串。

代码实现

首先在kmp算法中最主要的next数组，这个数组标志着截止到当前下标的最长前缀后缀匹配子串字符个数，kmp算法里面，如果某个前缀是好前缀，即与模式串前缀匹配，我们就可以利用一定的技巧不止向前滑动一个字符，具体看前面的讲解。我们提前不知道哪些是好前缀，并且匹配过程不止一次，因此我们在最开始调用一个初始化方法，初始化next数组。

1.如果上一个字符的最长前缀子串的下一个字符==当前字符，上一个字符的最长前缀子串直接加上当前字符即可

2.如果不等于，需要找到之前存在的最长前缀子串的下一个字符等于当前子串的，然后设置当前字符子串的最长前缀后缀子串

int[] next ;
    /**
     * 初始化next数组
     * @param modelStr
     */
    public void init(char[] modelStr) {
        //首先计算next数组
        //遍历modelStr，遍历到的字符与之前字符组成一个串
        next = new int[modelStr.length];
        int start = 0;
        while (start < modelStr.length) {
            next[start] = this.recursion(start, modelStr);
            ++ start;
        }
    }

    /**
     *
     * @param i 当前遍历到的字符
     * @return
     */
    private int recursion(int i, char[] modelStr) {
        //next记录的是个数，不是下标
        if (0 == i) {
            return 0;
        }
        int last = next[i -1];
        //没有匹配的,直接判断第一个是否匹配
        if (0 == last) {
            if (modelStr[last] == modelStr[i]) {
                return 1;
            }
            return 0;
        }
        //如果last不为0，有值，可以作为最长匹配的前缀
        if (modelStr[last] == modelStr[i]) {
            return next[i - 1] + 1;
        }
        //当next[i-1]对应的子串的下一个值与modelStr不匹配时，需要找到当前要找的最长匹配子串的次长子串
        //依据就是次长子串对应的子串的下一个字符==modelStr[i];
        int tempIndex = i;
        while (tempIndex > 0) {
            last = next[tempIndex - 1];
            //找到第一个下一个字符是当前字符的匹配子串
            if (modelStr[last] == modelStr[i]) {
                return last + 1;
            }
            -- tempIndex;
        }
        return 0;
    }

然后开始利用next数组进行匹配，从第一个字符开始匹配进行匹配，找到第一个不匹配的字符，这时候之前的都是匹配的，接下来先判断是否已经是完全匹配，是直接返回，不是，判断是否第一个就不匹配，是直接往后面匹配。如果有好前缀，这时候就利用到了next数组，通过next数组知道当前可以从哪个开始匹配，之前的都不用进行匹配。

public int kmp(char[] mainStr, char[] modelStr) {
        //开始进行匹配
        int i = 0, j = 0;
        while (i + modelStr.length <= mainStr.length) {
            while (j < modelStr.length) {
                //找到第一个不匹配的位置
                if (modelStr[j] != mainStr[i]) {
                    break;
                }
                ++ i;
                ++ j;
            }
            if (j == modelStr.length) {
                //证明完全匹配
                return i - j;
            }
            //走到这里找到的是第一个不匹配的位置
            if (j == 0) {
                ++ i;
                continue;
            }
            //从好前缀后一个匹配
            j = next[j - 1];
        }
        return -1;
    }

到此这篇关于详解Java中KMP算法的图解与实现的文章就介绍到这了,更多相关Java KMP算法内容请搜索脚本之家以前的文章或继续浏览下面的相关文章希望大家以后多多支持脚本之家！