Pytorch学习笔记（七）——CNN基础

一、卷积 （互相关）运算

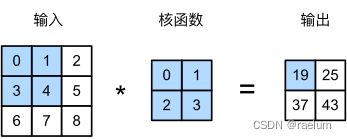
严格来讲，卷积运算实际上是互相关（cross-correlation）运算，如下图所示：

设输入大小为 $(n_h,n_w)$，卷积核大小为 $(k_h,k_w)$，则输出大小为 $(n_h-k_h+1,n_w-k_w+1)$

接下来实现卷积运算：

class Conv2D(nn.Module):
    def __init__(self, kernel_size):
        super().__init__()
        # 随机初始化卷积核的权重和偏置
        self.weight = nn.Parameter(torch.randn(kernel_size))
        self.bias = nn.Parameter(torch.zeros(1))
        
    def forward(self, X):
        return self.corr2d(X, self.weight) + self.bias
    
    def corr2d(self, X, K):
        h, w = K.shape
        Y = torch.zeros(X.shape[0] - h + 1, X.shape[1] - w + 1)
        for i in range(Y.shape[0]):
            for j in range(Y.shape[1]):
                Y[i, j] = torch.sum(X[i:i + h, j:j + w] * K)
        return Y

测试：

torch.manual_seed(42)
conv2d = Conv2D((3, 3))
X = torch.randn(5, 5)
Y = conv2d(X)
print(Y)
# tensor([[-2.1781,  0.0133, -0.8048],
#         [ 1.3521, -0.5629,  0.0579],
#         [-3.0277,  0.6740,  0.7058]], grad_fn=)

1.1 边缘检测

先创建一个黑白图，假设 $1$ 代表白色，$0$ 代表黑色：

X = torch.ones((6, 8))
X[:, 2:6] = 0
X
# tensor([[1., 1., 0., 0., 0., 0., 1., 1.],
#         [1., 1., 0., 0., 0., 0., 1., 1.],
#         [1., 1., 0., 0., 0., 0., 1., 1.],
#         [1., 1., 0., 0., 0., 0., 1., 1.],
#         [1., 1., 0., 0., 0., 0., 1., 1.],
#         [1., 1., 0., 0., 0., 0., 1., 1.]])

接下来，我们构造一个形状为 $(1,2)$ 的卷积核。当进行互相关运算时，如果水平相邻的两元素相同，则输出为零，否则输出为非零。

conv2d = Conv2D((1, 2))
conv2d.weight.data = torch.tensor([[-1., 1.]])
conv2d(X)
# tensor([[ 0., -1.,  0.,  0.,  0.,  1.,  0.],
#         [ 0., -1.,  0.,  0.,  0.,  1.,  0.],
#         [ 0., -1.,  0.,  0.,  0.,  1.,  0.],
#         [ 0., -1.,  0.,  0.,  0.,  1.,  0.],
#         [ 0., -1.,  0.,  0.,  0.,  1.,  0.],
#         [ 0., -1.,  0.,  0.,  0.,  1.,  0.]], grad_fn=)

该卷积核只能检测垂直边缘，无法检测水平边缘。

1.2 nn.Conv2d

我们可以使用 nn.Conv2d 来更方便地构造卷积层，格式如下：

nn.Conv2d(in_channels, out_channels, kernel_size, stride=1, padding=0, bias=True)

这里仅列出了常用的参数。其中 in_channels 表示输入通道数，out_channels 表示输出通道数，kernel_size 为卷积核的大小（元组形式），stride 为步幅，padding 为填充，bias 表示是否开启偏置。

输入的形状为 $(B,C_{in},H_{in},W_{in})$（或 $(C_{in},H_{in},W_{in})$），输出的形状为 $(B,C_{out},H_{out},W_{out})$（或 $(C_{out},H_{out},W_{out})$），其中 $B$ 是 batch size。

X = torch.ones((6, 8))
X[:, 2:6] = 0
X = X.reshape((1, 6, 8))

conv2d = nn.Conv2d(1, 1, (1, 2), bias=False)
conv2d.weight.data[0, 0] = torch.tensor([[-1., 1.]])
conv2d(X)
# 结果与1.1中的一样

注意只有 conv2d.weight.data[0, 0] 才是有效的，conv2d.weight[0, 0].data 无效。

1.3 卷积核学习

如果我们只需寻找黑白边缘，那么以上卷积核足以完成任务。然而，当有了更复杂数值的卷积核，或者连续的卷积层时，我们不可能手动设计卷积核。那么我们是否可以学习由 X 生成 Y 的卷积核呢？

答案是可以的。

# 给定 X 和 Y
X = torch.ones(6, 8)
Y = torch.zeros(6, 7)

X[:, 2:6] = 0
Y[:, 1] = -1
Y[:, -2] = 1

X = X.reshape((1, 6, 8))
Y = Y.reshape((1, 6, 7))

# 初始化
conv2d = nn.Conv2d(1, 1, (1, 2), bias=False)
optimizer = torch.optim.SGD(conv2d.parameters(), lr=1e-2)
num_epochs = 100

# 学习
for epoch in range(num_epochs):
    Y_hat = conv2d(X)
    loss = torch.norm(Y_hat - Y) ** 2
    # 反向传播
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()

print(conv2d.weight.data.reshape((1, 2)))
# tensor([[-1.0000,  1.0000]])

可以看出结果与我们预先使用的卷积核几乎是完全相同的。

1.4 特征图与感受野

假设一张图片转化为张量后，其形状为 $n_c\times n_h\times n_w$，其中 $n_c$ 是通道个数，对于RGB彩图应有 $n_c=3$。自然地，卷积核的形状应为 $n_c\times k_h\times k_w$，即卷积核的通道数应与输入的通道数保持一致。

只用一个卷积核，则卷积之后的输出的形状为 $(n_h-k_h+1,n_w-k_w+1)$，即三维卷积之后得到了二维的张量，而这个二维的张量就称作特征图（feature map）。

二维卷积可以形象的理解为两个网格正方形按元素相乘后再全部相加，从而三维卷积就是两个网格正方体按元素相乘后再全部相加。

对于特征图上的某个元素 $x$，其感受野（receptive field）则是指在正向传播期间可能影响计算 $x$ 的所有元素（来自所有先前层）。

二、填充和步幅

2.1 填充

在应用多层卷积时，我们常常丢失边缘像素。 由于我们通常使用小卷积核，因此对于任何单个卷积，我们可能只会丢失几个像素。 但随着我们应用许多连续卷积层，累积丢失的像素数就多了。 解决这个问题的简单方法即为填充（padding）：在输入图像的边界填充元素（通常填充元素是 $0$）。

为简便起见，接下来我们假设图片和卷积核均为正方形，尺寸分别为 $n\times n$ 和 $f\times f$。假设在图片周围补 $p$ 圈 $0$，则输出尺寸为

$$(n-f+2p+1)\times (n-f+2p+1)$$

通常卷积核的高度和宽度均为奇数，因此若填充 $(f-1)/2$ 圈 $0$，则得到的特征图尺寸与输入尺寸一致。

考虑 $32\times 32$ 的单通道图像，设卷积核的尺寸为 $5\times 5$，若填充选择 $2$，则输出尺寸不变：

X = torch.randn(1, 32, 32)
conv2d = nn.Conv2d(1, 1, (5, 5), padding=2)
Y = conv2d(X)
Y.shape
# torch.Size([1, 32, 32])

2.2 步幅

在前面的例子中，我们默认每次滑动一个元素。 但是，有时候为了高效计算或是缩减采样次数，卷积窗口可以跳过中间位置，每次滑动多个元素。

我们将每次滑动元素的数量称为步幅（stride），步幅分为垂直步幅和水平步幅两种，这里我们假设垂直步幅和水平步幅相同。

设步幅为 $s$，则输出尺寸为

$$\lfloor \frac{n-f+2p}{s}+1\rfloor \times \lfloor \frac{n-f+2p}{s}+1\rfloor$$

依然考虑 $32\times 32$ 的单通道图像，设卷积核的尺寸为 $5\times 5$，若填充为 $3$，步幅为 $3$，则输出尺寸应为 $12\times 12$：

X = torch.randn(1, 32, 32)
conv2d = nn.Conv2d(1, 1, (5, 5), stride=3, padding=3)
Y = conv2d(X)
Y.shape
# torch.Size([1, 12, 12])

三、多输入输出通道

通常我们的输入都是多通道的，例如对于一张RGB图片来说，其形状为 $3\times n_h\times n_w$，本章节我们考虑更一般的形式，即假设输入的形状为 $c_i\times n_h\times n_w$。

当输入包含多个通道时，需要构造一个与输入数据具有相同输入通道数的卷积核，以便与输入数据进行三维卷积，即单个卷积核的形状应当为 $c_i\times k_h\times k_w$。在填充 $0$，步幅 $1$ 的前提下，该卷积核与原图进行三维卷积后可以得到一个形状为 $(n_h-k_h+1,n_w-k_w+1)$ 的特征图。若有多个卷积核，则会产生多个特征图，而输出的特征图的数量即为输出通道的个数，记为 $c_o$。因此一组卷积核的形状可以表示为 $c_o\times c_i\times k_h\times k_w$。

例如，现有一张 $28\times 28$ 的RGB图，转化为张量后的形状为 $3\times 28\times 28$，即输入通道数为 $3$。若输出通道数为 $6$，这意味着我们有 $6$ 个形状为 $3\times k_h\times k_w$ 的卷积核，卷积后可得到 $6$ 个特征图。若固定卷积核的大小为 $5\times 5$，使用默认的填充和步幅，则输出的形状为 $6\times 24\times 24$。接下来使用程序进行验证：

X = torch.randn(3, 28, 28)
conv2d = nn.Conv2d(3, 6, (5, 5))
Y = conv2d(X)
Y.shape
# torch.Size([6, 24, 24])

图像在卷积神经网络中进行传递时，通常 $n_h,n_w$ 会逐渐减小，$n_c$ 会逐渐增大。

四、汇聚层（池化层）

与卷积层类似，汇聚层运算由一个固定形状的窗口组成，该窗口根据其步幅大小在输入的所有区域上滑动，为滑动窗口遍历的每个位置计算一个输出。不同于卷积层，汇聚层中不包含任何参数，并且汇聚运算是确定性的，我们通常计算滑动窗口中所有元素的最大值或平均值。

汇聚层常用的超参数：滑动窗口的形状，填充和步幅。

torch.manual_seed(0)
X = torch.randint(1, 10, (1, 5, 5)).to(torch.float)
X
# tensor([[[9., 1., 3., 7., 8.],
#          [7., 8., 2., 2., 1.],
#          [9., 3., 7., 4., 2.],
#          [3., 1., 1., 6., 4.],
#          [9., 3., 9., 3., 9.]]])
pool2d = nn.MaxPool2d(3, stride=1)
pool2d(X)
# tensor([[[9., 8., 8.],
#          [9., 8., 7.],
#          [9., 9., 9.]]])
pool2d = nn.AvgPool2d(3, stride=1)
pool2d(X)
# tensor([[[5.4444, 4.1111, 4.0000],
#          [4.5556, 3.7778, 3.2222],
#          [5.0000, 4.1111, 5.0000]]])

汇聚层的输出通道数与输入通道数相同。