Python调用scikit-learn实现机器学习

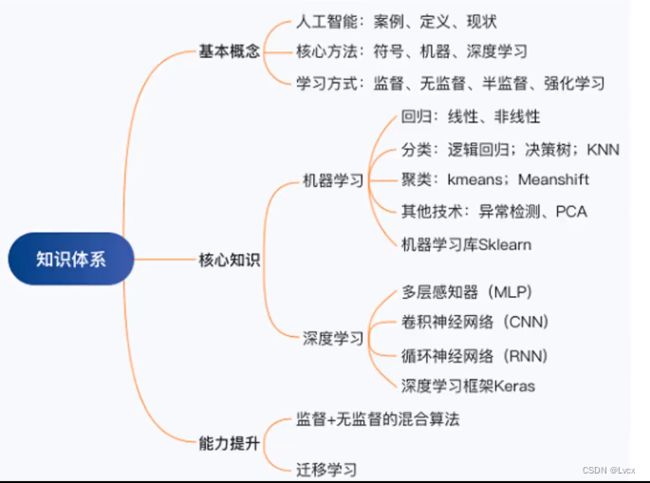
第一章 机器学习介绍及环境部署

1-1 课程介绍

1. 课程目标

1.了解人工智能（AI）及其主流算法

• AI是什么、有什么特点；机器学习与AI的关系。

2.熟练使用python及scikit-learn工具包

• 环境配置与安装、基本语法、数据操作。

3.掌握完成机器学习任务的能力

• 数据预处理、模型加载、训练及预测。

4.运用不同的机器学习模型、评估模型表现

• K-邻近（KNN）算法、逻辑回归；混淆矩阵。

2. 课程目录

1. 机器学习介绍及其原理
2. 及其学习开发环境部署
3. 机器学习实现之数据预处理
4. 机器学习实现之模型训练
5. 机器学习实现之模型评估

3. 机器学习介绍及其原理

• 人工智能、机器学习是什么？
• 机器学习的主要类别有哪些？（监督式学习、非监督式学习、强化学习）
• 机器学习案例介绍
• 机器学习的基本原理

4. 什么是人工智能

• 人工智能就其本质而言，是机器对人的思维信息过程的模拟，让机器能向人一样思考。
  
  举例：电影兴趣度判断。
• 根据输入信息进行模型结构、权重更新，实现最终优化。
• 特点：信息处理、自我学习、优化升级。

5. 人工智能核心方法：机器学习、深度学习

• 机器学习是一种实现人工智能的方法，深度学习是一种实现机器学习的技术。
• 举例：空间点距求解。
  
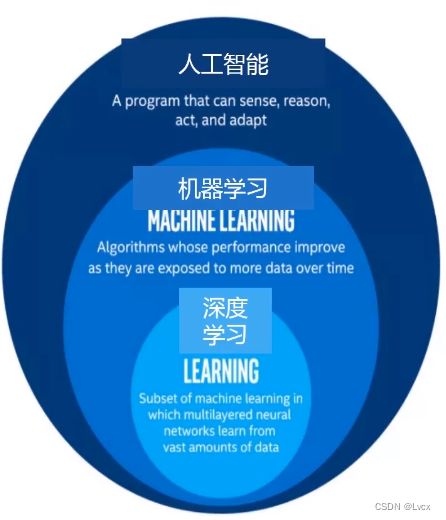
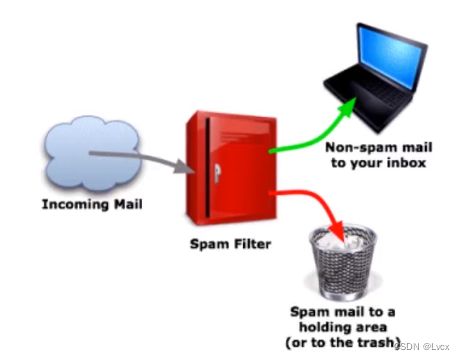
• 机器学习：使用算法来解析数据、从中学习，然后对真实世界中的事件做出决策和预测。比如：垃圾邮件检测、房价预测。
• 深度学习：模仿人类神经网络，建立模型，进行数据分析。比如：人脸识别、语义理解、无人驾驶。

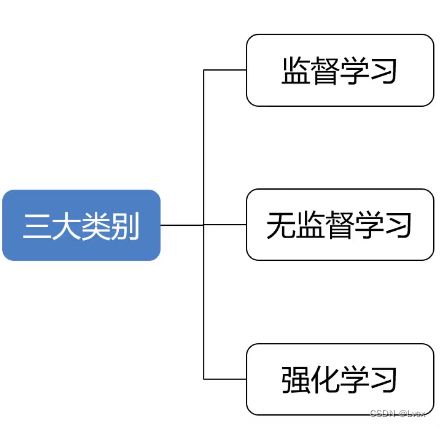
6. 机器学习的主要类别有哪些？

1. 监督式学习

• 基于数据及结果进行预测。
• 举例：垃圾邮件检测、房价预测。
• 特点：一组输入数据对应一个“正确的”输出结果。（即有输入数据和标签）

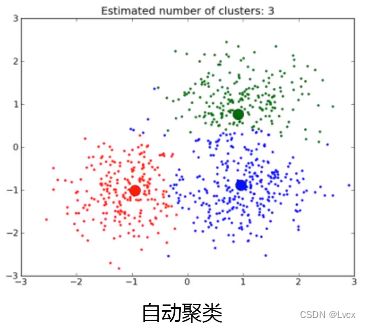
2. 非监督式学习

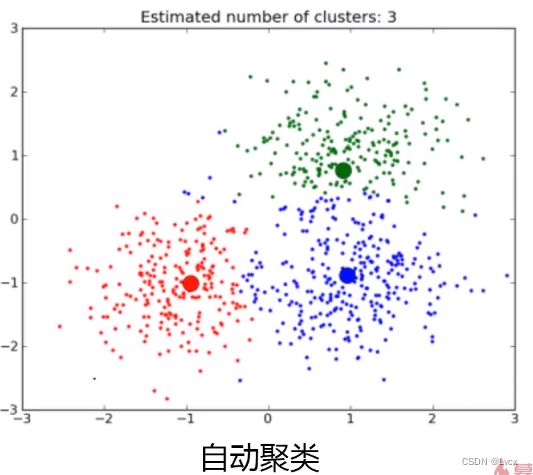
• 从数据中挖掘关联性。
• 举例：数据聚类、相关新闻自动推送。
• 特点：不存在“正确的”答案。（有数据，无标签）

3. 强化学习

• 会根据你给机器的奖励和惩罚，让机器自动地去寻找模型的结构或者是数据的规律。

7. 机器学习的基本原理

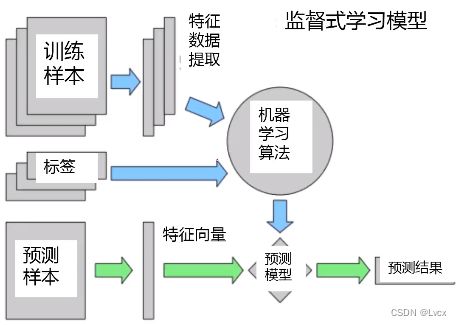
1. 监督式学习

监督式学习核心步骤：

1. 使用标签数据训练机器学习模型。

• “标签数据”是指由输入数据对应的正确的输出结果。
• “机器学习模型”将学习输入数据与之对应的输出结果间的函数关系。

2. 调用训练好的机器学习模型，根据新的输入数据预测对应的结果。
   

2. 非监督式学习

• 相比与监督式学习，非监督式学习不需要标签数据，而是通过引入预先设定的优化准则进行模型训练，比如自动将数据分为三类。
  

1-2 开发环境介绍

1. Python介绍

• Python是一种解释型的、面向对象的、移植性强的高级程序设计语言。
• 开发者：吉多·范罗苏姆（Guide van Rossum）

1. 解释型：不需要编译成二进制代码，可以直接从源代码运行。
2. 面向对象：Python既支持面向过程编程，也支持面向对象编程。
3. 高层语言：无需考虑如何管理程序使用的内存一类的底层细节。

优点：

• 简单易学
• 开发效率高
• 高级语言
• 可移植性
• 可扩展性
• 可嵌入性

缺点：

• 速度慢
• 代码不能加密

2. scikit-learn介绍

• Python语言中专门针对机器学习应用而发展起来的一款开源框架（算法库），可以实现数据预处理、分类、回归、降维、模型选择等常用的机器学习算法。

特点：

• 集成了机器学习中各类成熟的算法，容易安装和使用，样例丰富，教程和文档也非常详细。
• 不支持Python之外的语言，不支持深度学习和强化学习。
  Scikit-learn官网：https://scikit-learn.org/stable/

3. jupyter notebook介绍

• jupyter Notebook是一个开源的Web应用程序，旨在方便开发者创建和共享代码文档。用户可以在里面写代码、运行代码、查看结果，并在其中可视化数据。
  特点：
• 允许把代码写入独立的cell中，然后单独执行。用户可以在测试项目时单独测试特定代码块，无需从头开始执行代码。
• 基于web框架进行交互开发，非常方便。
  jupyter官网：https://jupyter.org/

1-3 开发环境部署

1. 安装Python
2. 安装anaconda
3. 新建开发环境、安装numpy、scikit-learn库

conda create -n 环境名
pip(conda) install 包名

4. jupyter notebook界面优化
   参考：https://github.com/dunovank/jupyter-themes
   安装相应的优化界面的包：pip install jupyterthemes
   进行界面设置：jt -t ocens16 -f fira -fs 17 -cellw 90% -ofs 14 -dfs 14 -T

第二章 机器学习变编程实战

2-1 数据预处理：iris数据介绍、数据加载、数据展示、维度确认

1. 目标

• iris数据集是什么、它与机器学习有什么关系。
• 如何通过scikit-learn加载iris数据。
• 如何进行数据展示。
• 使用scikit-learn进行数据处理的四个关键点。

2. Iris数据集

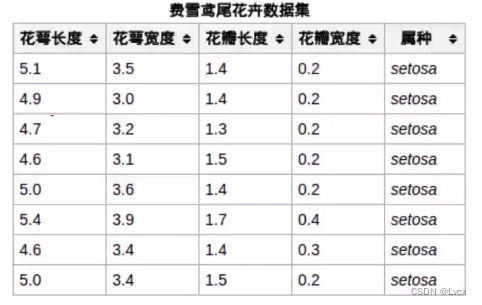
• Iris鸢尾花数据集是一个经典数据集，在统计学习和机器学习领域都经常被用作示例。
• 有3类，共150条记录，每类各50个数据。
• 每条记录都有4项特征：花萼长度（Sepal Length）、花萼宽度（Sepal Width）、花瓣长度（Petal Length）、花瓣宽度（Petal Width），可以通过这4个特征预测鸢尾花卉属于（iris-setosa、iris-versicolour、iris-virginica）中的哪一品种。
  

1. iris数据集在机器学习的应用

• 属于监督式学习应用：根据花的四个特征预测鸢尾花卉属于（iris-setosa、iris-versicolour、iris-virginica）中的哪一品种。
• 机器学习经典案例，原因：简单而具有代表性。

3. 使用Python进行基本的数据操作

• iris数据加载
• 数据展示
• 确认数据维度
• 使用scikit-learn进行数据处理的四个关键点
  • 1.区分属性数据和结果数据
  • 2.属性数据与结果数据都是量化的
  • 3.运算过程中，属性数据与结果数据的类型都是Numpy数组
  • 4.属性数据与结果数据的维度是对应的

4. 代码实战

# Iris数据加载
from sklearn import datasets
iris = datasets.load_iris()


# 展示iris数据
print(iris.data)
# 每一行数据是一个样本
# 每一列数据代表不同样本同一属性下对应的数值


# 查看对应属性名称
print(iris.feature_names)


# 查看输出的结果
print(iris.target)


# 查看结果的含义
print(iris.target_names)   
# 对应3种类别


# 分类问题 是对应结果为类别（非连续性）的监督式学习问题
# 每个预测的数值即是结果数据（或称为：目标、输出、标签）


# 确认数据类型
print(type(iris.data))


print(type(iris.target))


# 确认维度
print(iris.data.shape) 
# 150行、4列


print(iris.target.shape)
# 150行，1列


# X是输入数据赋值，y是输出数据赋值
X = iris.data
y = iris.target


print(X)


print(y)

2-2 模型训练：分类问题、KNN模型、模型加载、训练、预测

1. 目标

• Iris数据回顾
• 分类问题介绍
• K近邻分类模型介绍
• 使用scikit-learn进行模型训练与预测的四步骤

2. 分类问题介绍

• Email：是否为垃圾邮件？
  
• 动物：识别图片中的动物是猫还是狗
  
• iris花：鸢尾花识别
  
  分类：根据数据集目标的特征或属性，划分到已有的类别中。
  常用的分类算法：K近邻（KNN）、逻辑回归、决策树、朴素贝叶斯。

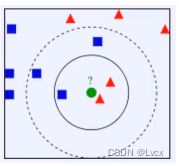
3. K近邻分类模型（KNN）

• 给定一个训练数据集，对新的输入实例，在训练数据集中找到与该实例最邻近的K个实例（也就是上面所说的K个邻居），这K个实例的多数属于某个类，就把该输入实例分类到这个类中。

• 通俗来说，如果一个样本在特征空间中的K个最相似（即特征空间中最邻近）的样本中的大多数属于某一个类别，则该样本也属于这个类别。该方法在定类决策上只依据最邻近的一个或者几个样本的类别来决定待分样本所属的类别。

• 该方法的不足之处是计算量较大，因为对每一个待分类的文本都要计算它到全体已知样本的距离，才能求得它的K个最邻近点。目前常用的解决方法是事先对已知样本点进行剪辑，事先去除对分类作用不大的样本。另外还有一种 Reverse KNN法，它能降低KNN算法的计算复杂度，提高分类的效率。

• KNN算法比较适用于样本容量比较大的类域的自动分类，而那些样本容量较小的类域采用这种算法比较容易产生误分。

• 最简单的机器学习算法之一。

• 举例：

• 

  • K=3，绿色源点的最近的3个邻居是2个红色小三角形和1个蓝色小正方形，判定绿色的待分类点属于红色的三角形一类。
  • 如果K=5，绿色源点的最近的5个邻居是2个红色三角形和3个蓝色的正方形，判定绿色的待分类点属于蓝色的正方形一类。

4. KNN分类图

5. 使用scikit-learn进行模型训练与预测

• iris数据加载
• 使用scikit-learn建模四步骤
  • 1.调用需要使用的模型类
  • 2.模型初始化（创建一个模型实例）
  • 3.模型训练
  • 4.模型预测

6. 代码实战

# iris数据加载


# 通过sklearn自带数据包加载iris数据
from sklearn import datasets
iris = datasets.load_iris()
# 样本数据与结果分别赋值给“X”，“y”
X = iris.data
y = iris.target


# 确认样本和输出数据维度
print("X维度：", X.shape)
print("y维度：", y.shape)


# 模型调用
from sklearn.neighbors import KNeighborsClassifier


# 创建实例
knn = KNeighborsClassifier(n_neighbors=1)


print(knn)


# 模型训练(拟合)
knn.fit(X, y)


# 进行样本的预测
knn.predict([[1, 2, 3, 4]])

# 同时预测多个样本
x_test = [[1, 2, 3, 4], [2, 4, 1, 2]]
knn.predict(x_test)


# 设定一个新的K值进行KNN建模
knn_5 = KNeighborsClassifier(n_neighbors=5)
# 确认模型结构的方法：在上一行代码的小括号中按Shift + Tab键


knn_5.fit(X, y)
knn_5.predict(x_test)

2-3 模型评估一：准确率、数据分离、参数选择

1. 目标

• 模型训练回顾
• 模型评估：全数据集训练与预测
• 模型评估：训练数据集、测试数据集分离
• 如何为模型选择合适的关键参数，预测新数据对应结果

2. 模型训练回顾

• 分类任务：根据花特征数据预测其所属的品种
• 已使用分类模型：K近邻分类（K=1），K近邻分类（K=5）
• 需要一个选择合适模型额方法
  解决办法：尝试模型评估流程。

3. 评估流程：

1. 将整个数据集用于训练与测试

1. 使用整个数据集进行模型训练
2. 使用相同的数据集进行测试，并通过对比预测结果与实际结果来评估模型表现

1. 准确率：

• 正确预测的比例
• 用于评估分类模型表现的常用指标

2. 训练数据与测试数据相同导致的问题：

• 训练模型的最终目标是为了预测新数据对应的结果
• 最大化训练准确率通常会导致模型复杂化（比如增加维度），因此将降低模型的通用性
• 过度复杂模型容易导致训练数据的过度拟合（绿色线）
  

2. 分离训练数据与测试数据

1. 步骤：

1. 把数据分成两部分：训练集、测试集
2. 使用训练集数据进行模型训练
3. 使用测试集数据进行预测，从而评估模型表现
   

2. 分离训练集与测试集数据的作用：

• 可以实现在不同的数据集上进行模型训练与预测
• 建立数学模型的目的是对新数据的预测，基于测试数据计算的准确率能更有效地评估模型表现

3. 模型关键参数选择：

目标：确定合适的参数（组），提高模型预测准确率
方法：

• 1.遍历参数组合，建立对应的模型
• 2.使用训练集数据进行模型训练
• 3.使用测试集数据进行预测，评估每个模型表现
• 4.通过图形展示参数（组）与准确率的关系，确定合适的参数（组）

4. 代码实战

# 评估流程：1. 将整个数据集用于训练与测试
# 1. 使用整个数据集进行模型训练
# 2. 使用相同的数据集进行测试，并通过对比测结果与实际结果来评估模型表现


# 数据加载 模型训练与预测
from sklearn import datasets
iris = datasets.load_iris()
X = iris.data
y = iris.target


from sklearn.neighbors import KNeighborsClassifier
knn_5 = KNeighborsClassifier(n_neighbors = 5)
# 训练模型
knn_5.fit(X, y)


y_pred = knn_5.predict(X)
print(y_pred)
print(y_pred.shape)


# 准确率：
	# 正确预测的比例
	# 用于评估分类模型表现的常用指标



# 准确率计算
from sklearn.metrics import accuracy_score
print(accuracy_score(y, y_pred))


# K近邻分类KNN（K = 1）


knn_1 = KNeighborsClassifier(n_neighbors = 1)
knn_1.fit(X, y)
y_pred = knn_1.predict(X)
print(accuracy_score(y, y_pred))



# 训练数据与测试数据相同导致的问题：
	# 训练模型的最终目标是为了预测新数据对应的结果
	# 最大化训练准确率通常会导致模型复杂化（比如增加维度），因此将降低模型的通用性
	# 过度复杂模型容易导致训练数据的过度拟合


# 确认数据条数
print(X.shape)  # 150条
print(y.shape)


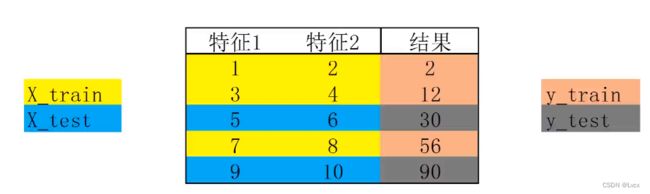
# 数据分离
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.4)    # 训练的数据，测试的数据、训练的结果、测试的结果


# 分离后，数据集的维度确认
print(X_train.shape)  # 训练的数据
print(X_test.shape)   # 测试的数据
print(y_train.shape)  # 训练的结果
print(y_test.shape)   # 测试的结果


# 分离训练集与测试集数据的作用：
	# 可以实现在不同的数据集上进行模型训练与预测
	# 建立数学模型的目的是对新数据的预测，基于测试数据计算的准确率能更有效地评估模型表现


# 分离后，数据集的训练和评估
knn_5_s = KNeighborsClassifier(n_neighbors = 5)
knn_5_s.fit(X_train, y_train)
y_train_pred = knn_5_s.predict(X_train)
y_test_pred = knn_5_s.predict(X_test)


# 查看分离后在训练集上模型预测的准确率
print(accuracy_score(y_train, y_train_pred))


# 查看分离后在测试集上模型预测的准确率
print(accuracy_score(y_test, y_test_pred))


# KNN模型(K=1)
knn_1_s = KNeighborsClassifier(n_neighbors = 1)
knn_1_s.fit(X_train, y_train)
y_train_pred = knn_1_s.predict(X_train)
y_test_pred = knn_1_s.predict(X_test)


# 查看准确率
print(accuracy_score(y_train, y_train_pred))
print(accuracy_score(y_test, y_test_pred))


# 如何确定更合适的K值
	# K ：1-25
	# 遍历所有可能的参数组合
	# 建立相应的模型
	# 模型的训练以及预测
	# 基于测试数据的准确率计算
	# 查看最高的准确率对应的K值


k_range = list(range(1, 26))
print(k_range)


# 定义存储所有训练集准确率和测试集准确率的列表
score_train = []
score_test = []
for k in k_range:
    knn = KNeighborsClassifier(n_neighbors = k)
    # 训练模型
    knn.fit(X_train, y_train)
    # 预测模型
    y_train_pred = knn.predict(X_train)
    y_test_pred = knn.predict(X_test)
    # 获得准确率
    train_score = accuracy_score(y_train, y_train_pred)
    test_score = accuracy_score(y_test, y_test_pred)
    # 保存每一次的准确率
    score_train.append(train_score)
    score_test.append(test_score)


# 训练集的准确率
for k in k_range:
    print(k, score_train[k - 1])


# 测试集的准确率
for k in k_range:
    print(k, score_test[k - 1])


# 用图形展示准确率
# 导入matplotlib模块并使图像在notebook中展示
import matplotlib.pyplot as plt
# -*- coding: utf-8 -*-
%matplotlib inline  
# 直接在界面展示结果

# 展示k值与训练数据集预测准确率之间的关系
plt.plot(k_range, score_train)  # x轴，y轴数据
plt.xlabel("K(KNN model)")
plt.ylabel("Training Accuracy")


# 导入matplotlib模块并使图像在notebook中展示
import matplotlib.pyplot as plt
# -*- coding: utf-8 -*-
%matplotlib inline  
# 直接在界面展示结果

# 展示k值与测试数据集预测准确率之间的关系
plt.plot(k_range, score_test)  # x轴，y轴数据
plt.xlabel("K(KNN model)")
plt.ylabel("Testing Accuracy")


# 训练数据集准确率 随着模型复杂而提高
# 测试数据集准确率 在模型过于简单或过于复杂的情况下更低
# KNN模型中，模型复杂度由K值决定（K越小，模型复杂度越高）


# 对新数据进行预测
knn_6 = KNeighborsClassifier(n_neighbors = 6)
knn_6.fit(X_train, y_train)
y_pred = knn_6.predict([[1, 2, 3, 4]])
print(y_pred)

2-4 模型评估二：逻辑回归、混淆矩阵、召回率、F1分数

1. 目标

• 逻辑回归模型（在二分类问题用使用广泛）
• 皮马印第安人糖尿病数据集
• 使用准确率进行模型评估的局限性
• 混淆矩阵、模型衡量指标及其意义

2. 逻辑回归模型

• 用于解决分类问题的一种模型。根据数据特征或属性，计算其归属于某一类别的概率P(x)，根据概率数值判断其所属类别。主要应用场景：二分类问题。
• 数学表达式：
  
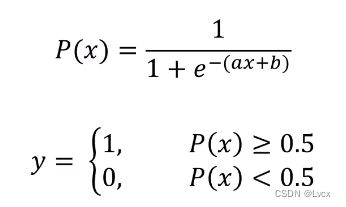
  其中，y为类别结果，P为概率，x为特征值，a、b为常量。
  

3. 皮马印第安人糖尿病数据集

• 简介：基于数据集中包括的某些诊断测量来诊断性地预测患者是否患有糖尿病。
• 输入变量：独立变量包括患者的怀孕次数、葡萄糖量、血压、皮褶厚度、体重指数、胰岛素水平、糖尿病谱系功能、年龄。
• 输出结果：是否患有糖尿病。
• 数据来源：Pima Indians Diabetes dataset
• 数据预览：
  
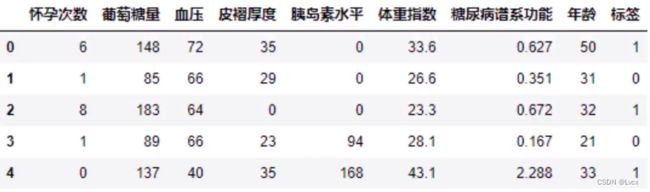
• 任务：通过怀孕次数、胰岛素水平、体重指数、年龄四个特征预测是否患有糖尿病。

4. 使用准确率进行模型评估的局限性

模型评估回顾：

• 目的：通过模型评估对比模型表现、确定合适的模型参数（组）。
• 方法：计算测试数据集预测准确率以评估模型表现。
  预测准确率的局限性：
• 无法真实反映模型针对各个分类的预测准确度。
  准确率可以方便的用于衡量模型的整体预测效果，但无法反应细节信息，具体表现在：
• 没有体现数据的实际分布情况。
• 没有体现模型错误预测的类型。
  

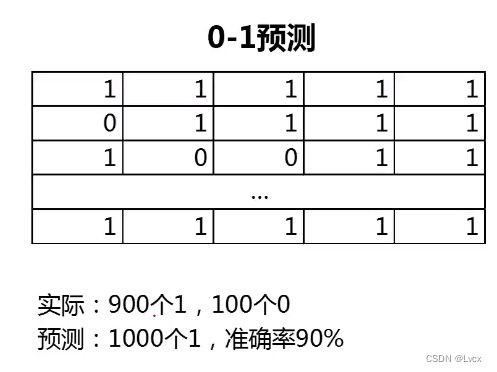
空准确率：当模型总是预测比例较高的类别，其预测准确率的数值。

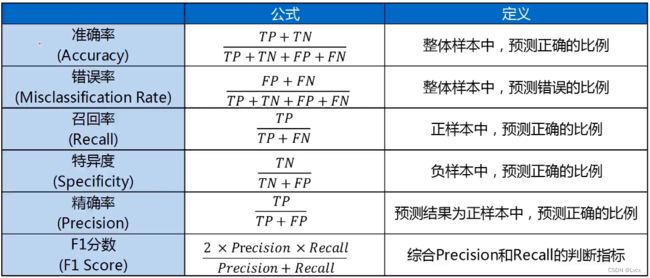
5. 混淆矩阵

• 混淆矩阵，又称为误差矩阵，用于衡量分类算法的准确程度。
  
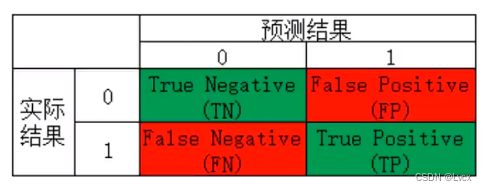
• True Positives(TP)：预测准确、实际为正样本的数量（实际为1，预测为1）
• True Negatives(TN)：预测准确、实际为负样本的数量（实际为0，预测为0）
• False Positives(FP)：预测错误、实际为负样本的数量（实际为0，预测为1）（错误地被预测成正样本）
• False Negatives(FN)：预测错误、实际为正样本的数量（实际为1，预测为0）（错误地被预测成负样本）

1. 混淆矩阵指标

2. 混淆矩阵指标特点：

• 分类任务中，相比单一的预测准确率，混淆矩阵提供了更全面的模型评估信息。
• 通过混淆矩阵，我们可以计算出多样的模型表现衡量指标，从而更好地选择模型。

3. 哪个衡量指标更关键？

• 衡量指标的选择取决于应用场景。
• 垃圾邮件检测（正样本为“垃圾邮件”）：希望普通邮件（负样本）不要被判断为垃圾邮件（正样本），需要关注精确率，希望判断为垃圾邮件的样本都是判断正确的；还需要关注召回率，希望所有的垃圾邮件尽可能被判断出来。
• 异常交易检测（正样本为“异常交易”）：希望所有的异常交易都被检测到，即判断为正常的交易中尽可能不存在异常交易，需要关注特异度。

6. 代码实战

# 逻辑回归模型
# 皮马印第安人糖尿病数据集
# 使用准确率进行模型评估的局限性
# 混淆矩阵、模型衡量指标及其意义


# 皮马印第安人糖尿病数据集
# 简介：基于数据集中包括的某些诊断测量来诊断性地预测患者是否患有糖尿病。
# 输入变量：独立变量包括患者的怀孕次数、葡萄糖量、血压、皮褶厚度、体重指数、胰岛素水平、糖尿病谱系功能、年龄。
# 输出结果：是否患有糖尿病。
# 数据来源：Pima Indians Diabetes dataset
# 任务：通过怀孕次数、胰岛素水平、体重指数、年龄四个特征预测是否患有糖尿病。


# 数据预处理
import pandas as pd
path = "./PimaIndiansdiabetes.csv"
pima = pd.read_csv(path)
pima.head()   # 展示前5行


# X，y赋值（从csv文件中取出需要用到的指标）
feature_names = ["Pregnancies", "Insulin", "BMI", "Age"]
X = pima[feature_names]   # 取出多列数据
y = pima.Outcome   # 取出最后一列的数据（最后一列表头“Outcome”）


# 维度确认
print(X.shape)
print(y.shape)


# 数据分离（分成训练数据集合测试数据集）
from sklearn.model_selection import train_test_split 
# random_state=0保证每一次分离是一样的
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)


# 查看分离后的维度
print(X_train.shape)  # 训练集数据
print(y_train.shape)  # 训练集标签
print(X_test.shape)   # 测试集数据
print(y_test.shape)   # 测试集标签


# 模型训练（逻辑回归模型）
from sklearn.linear_model import LogisticRegression
logreg = LogisticRegression()
logreg.fit(X_train, y_train)


# 测试数据集结果预测
y_test_pred = logreg.predict(X_test)


# 使用准确率进行评估
from sklearn import metrics
print(metrics.accuracy_score(y_test, y_test_pred))


# 预测准确率的局限性：无法真实反映模型针对各个分类的预测准确度。

# 任务：计算并对比预测模型预测准确率、空准确率。

# 空准确率：当模型总是**预测比例较高**的类别，其预测准确率的数值。


# 确认正负样本数据量
y_test.value_counts()


# 1的比例
y_test.mean()


# 0的比例
1 - y_test.mean()


# 空准确率
max(y_test.mean(), 1-y_test.mean())


# 分类准确率可以方便地用于衡量模型的整体预测效果，但无法反应细节信息，具体表现在：
	# 没有体现数据的实际分布情况
	# 没有体现模型的错误预测的类型


# 混淆矩阵：又称为误差矩阵，用于衡量分类算法的准确程度。


# 名词解释：
# True Positives（TP）：预测准确、实际为正样本的数量（实际为1，预测为1）
# True Negatives（TN）：预测准确、实际为负样本的数量（实际为0，预测为0）
# False Positives（FP）：预测错误、实际为负样本的数量（实际为0，预测为1）（错误地被预测成正样本）
# False Negatives（FN）：预测错误、实际为正样本的数量（实际为1，预测为0）（错误地被预测成负样本）


# 计算并展示混淆矩阵
print(metrics.confusion_matrix(y_test, y_test_pred))


# 展示部分实际结果（25组）
print("true: ", y_test.values[0 : 25])
print("pred: ", y_test_pred[0 : 25])


# 四个因子赋值
confusion = metrics.confusion_matrix(y_test, y_test_pred)
TN = confusion[0, 0]   # 行、列
FP = confusion[0, 1]
FN = confusion[1, 0]
TP = confusion[1, 1]
print("TN: ", TN)
print("FP: ", FP)
print("FN: ", FN)
print("TP: ", TP)


# 混淆矩阵指标


# 准确率：整体样本中，预测正确样本数的比例
# Accuracy = (TP + TN) / (TN + FP + FN + TP)

# 计算准确率：
# 方法一：
accuracy = (TP + TN) / (TP + TN + FN + FP)
print(accuracy)
# 方法二：
accuracy = metrics.accuracy_score(y_test, y_test_pred)
print(accuracy)


# 错误率：整体样本中，预测错误样本数的比例
# Misclassification = (FP + FN) / (TP + TN + FN + FP)

# 计算错误率：
# 方法一：
mis_rate = (FP + FN) / (TP + TN + FN + FP)
print(mis_rate)
# 方法二：
mis_rate = 1 - accuracy
print(mis_rate)


# 灵敏度（召回率）：正样本中，预测正确的比例
# Sensitivity = Recall = TP / (TP + FN)

# 计算召回率：
recall = TP / (TP + FN)
print(recall)


# 特异度：负样本中，预测正确的比例
# Specificity = TN / (TN + FP)

# 计算特异度：
specificity = TN / (TN + FP)
print(specificity)


# 精确率：预测结果为正的样本中，预测正确的比例
# Precision = TP / (TP + FP)


# 计算精确率：
precision = TP / (TP + FP)
print(Precision)


# F1分数：综合Precision和Recall的一个判断指标
# F1Score = 2 * Precision * Recall / (Precision + Recall) 


# 计算F1分数：
f1_score = 2 * precision * recall / (precision + recall)
print(f1_score)


# 结论：
# 分类任务中，相比单一的 预测准确率，混淆矩阵提供了更全面的模型评估信息。
# 通过混淆矩阵，我们可以计算出多样的模型表现衡量指标，从而更好地选择模型。
# 哪个指标更关键？
# 衡量指标的选择取决于应用场景
# 垃圾邮件检测（正样本为“垃圾邮件”）：希望普通话邮件（负样本）不要被判断为垃圾邮件（正样本），需要关注精确率，希望判断为垃圾邮件的样本都是正确的；还需要关注召回率，希望所有的垃圾邮件尽可能被判断出来。
# 异常交易检测（正样本为“异常交易”）：希望所有的异常交易都被检测到，即判断为正常的交易中尽可能不存在异常交易，需要关注特异度。

2-5 人工智能实战提升

进一步学习需要掌握的一些技术：


参考课程地址：https://www.imooc.com/learn/1174