人工智能-作业3:例题程序复现 PyTorch版
例题
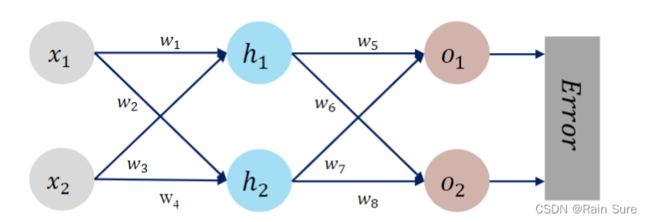
通过反向传播优化权值 w 1 w_1 w1, w 2 w_2 w2, … w 8 w_8 w8
输入值: x 1 x_1 x1 = 0.5, x 2 x_2 x2 = 0.3
输出值: y 1 y_1 y1 = 0.23, y 2 y_2 y2 = -0.07
激活函数全部为 S i g m o i d Sigmoid Sigmoid 函数
损失函数:MSE
初始权值:0.2, -0.4, 0.5, 0.6, 0.1, -0.5, -0.3, 0.8;
使用Pytorch实现
代码: 代码来源
# https://blog.csdn.net/qq_41033011/article/details/109325070
# https://github.com/Darwlr/Deep_learning/blob/master/06%20Pytorch%E5%AE%9E%E7%8E%B0%E5%8F%8D%E5%90%91%E4%BC%A0%E6%92%AD.ipynb
# torch.nn.Sigmoid(h_in)
import torch
x1, x2 = torch.Tensor([0.5]), torch.Tensor([0.3])
y1, y2 = torch.Tensor([0.23]), torch.Tensor([-0.07])
print("=====输入值:x1, x2;真实输出值:y1, y2=====")
print(x1, x2, y1, y2)
w1, w2, w3, w4, w5, w6, w7, w8 = torch.Tensor([0.2]), torch.Tensor([-0.4]), torch.Tensor([0.5]), torch.Tensor(
[0.6]), torch.Tensor([0.1]), torch.Tensor([-0.5]), torch.Tensor([-0.3]), torch.Tensor([0.8]) # 权重初始值
w1.requires_grad = True
w2.requires_grad = True
w3.requires_grad = True
w4.requires_grad = True
w5.requires_grad = True
w6.requires_grad = True
w7.requires_grad = True
w8.requires_grad = True
def sigmoid(z):
a = 1 / (1 + torch.exp(-z))
return a
def forward_propagate(x1, x2):
in_h1 = w1 * x1 + w3 * x2
out_h1 = sigmoid(in_h1) # out_h1 = torch.sigmoid(in_h1)
in_h2 = w2 * x1 + w4 * x2
out_h2 = sigmoid(in_h2) # out_h2 = torch.sigmoid(in_h2)
in_o1 = w5 * out_h1 + w7 * out_h2
out_o1 = sigmoid(in_o1) # out_o1 = torch.sigmoid(in_o1)
in_o2 = w6 * out_h1 + w8 * out_h2
out_o2 = sigmoid(in_o2) # out_o2 = torch.sigmoid(in_o2)
print("正向计算:o1 ,o2")
print(out_o1.data, out_o2.data)
return out_o1, out_o2
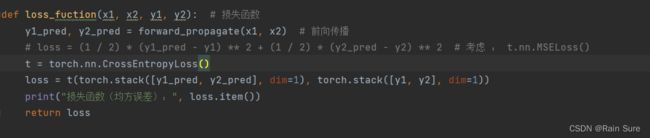
def loss_fuction(x1, x2, y1, y2): # 损失函数
y1_pred, y2_pred = forward_propagate(x1, x2) # 前向传播
loss = (1 / 2) * (y1_pred - y1) ** 2 + (1 / 2) * (y2_pred - y2) ** 2 # 考虑 : t.nn.MSELoss()
print("损失函数(均方误差):", loss.item())
return loss
def update_w(w1, w2, w3, w4, w5, w6, w7, w8):
# 步长
step = 1
w1.data = w1.data - step * w1.grad.data
w2.data = w2.data - step * w2.grad.data
w3.data = w3.data - step * w3.grad.data
w4.data = w4.data - step * w4.grad.data
w5.data = w5.data - step * w5.grad.data
w6.data = w6.data - step * w6.grad.data
w7.data = w7.data - step * w7.grad.data
w8.data = w8.data - step * w8.grad.data
w1.grad.data.zero_() # 注意:将w中所有梯度清零
w2.grad.data.zero_()
w3.grad.data.zero_()
w4.grad.data.zero_()
w5.grad.data.zero_()
w6.grad.data.zero_()
w7.grad.data.zero_()
w8.grad.data.zero_()
return w1, w2, w3, w4, w5, w6, w7, w8
if __name__ == "__main__":
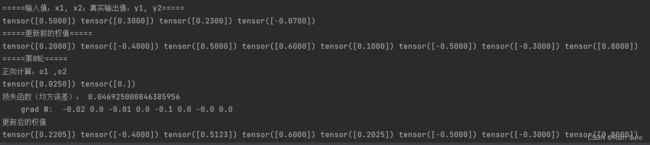
print("=====更新前的权值=====")
print(w1.data, w2.data, w3.data, w4.data, w5.data, w6.data, w7.data, w8.data)
for i in range(1):
print("=====第" + str(i) + "轮=====")
L = loss_fuction(x1, x2, y1, y2) # 前向传播,求 Loss,构建计算图
L.backward() # 自动求梯度,不需要人工编程实现。反向传播,求出计算图中所有梯度存入w中
print("\tgrad W: ", round(w1.grad.item(), 2), round(w2.grad.item(), 2), round(w3.grad.item(), 2),
round(w4.grad.item(), 2), round(w5.grad.item(), 2), round(w6.grad.item(), 2), round(w7.grad.item(), 2),
round(w8.grad.item(), 2))
w1, w2, w3, w4, w5, w6, w7, w8 = update_w(w1, w2, w3, w4, w5, w6, w7, w8)
print("更新后的权值")
print(w1.data, w2.data, w3.data, w4.data, w5.data, w6.data, w7.data, w8.data)
结果分析
1. 对比 【作业2】与【作业3】的程序,观察两种方法运行结果是否相同?
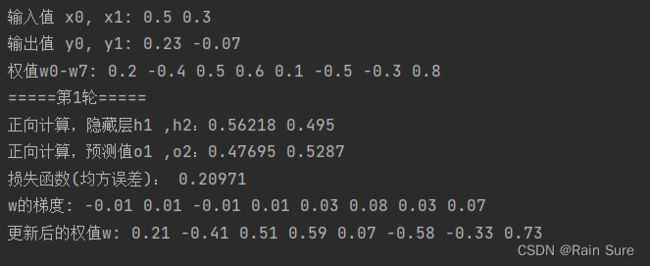
作业3运行结果:
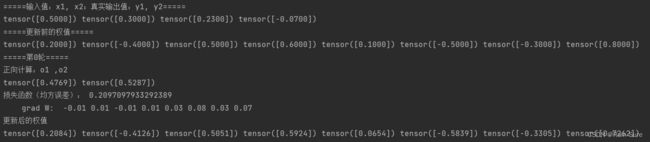
从运行结果来看,【作业2】与【作业3】的运行结果是不同的,【作业2】的运行结果是错误的。
2. 【作业2】程序更新
import numpy as np
w1, w2, w3, w4, w5, w6, w7, w8 = 0.2, -0.4, 0.5, 0.6, 0.1, -0.5, -0.3, 0.8
x1, x2 = 0.5, 0.3
y1, y2 = 0.23, -0.07
print("输入值 x0, x1:", x1, x2)
print("输出值 y0, y1:", y1, y2)
def sigmoid(z):
a = 1 / (1 + np.exp(-z))
return a
def forward_propagate(x1, x2, y1, y2, w1, w2, w3, w4, w5, w6, w7, w8):
in_h1 = w1 * x1 + w3 * x2
out_h1 = sigmoid(in_h1)
in_h2 = w2 * x1 + w4 * x2
out_h2 = sigmoid(in_h2)
in_o1 = w5 * out_h1 + w7 * out_h2
out_o1 = sigmoid(in_o1)
in_o2 = w6 * out_h1 + w8 * out_h2
out_o2 = sigmoid(in_o2)
print("正向计算,隐藏层h1 ,h2:", end="")
print(round(out_h1, 5), round(out_h2, 5))
print("正向计算,预测值o1 ,o2:", end="")
print(round(out_o1, 5), round(out_o2, 5))
error = (1 / 2) * (out_o1 - y1) ** 2 + (1 / 2) * (out_o2 - y2) ** 2
print("损失函数(均方误差):",round(error, 5))
return out_o1, out_o2, out_h1, out_h2
def back_propagate(out_o1, out_o2, out_h1, out_h2):
# 反向传播
d_o1 = out_o1 - y1
d_o2 = out_o2 - y2
d_w5 = d_o1 * out_o1 * (1 - out_o1) * out_h1
d_w7 = d_o1 * out_o1 * (1 - out_o1) * out_h2
d_w6 = d_o2 * out_o2 * (1 - out_o2) * out_h1
d_w8 = d_o2 * out_o2 * (1 - out_o2) * out_h2
d_w1 = (d_o1 * out_h1 * (1 - out_h1) * w5 + d_o2 * out_o2 * (1 - out_o2) * w6) * out_h1 * (1 - out_h1) * x1
d_w3 = (d_o1 * out_h1 * (1 - out_h1) * w5 + d_o2 * out_o2 * (1 - out_o2) * w6) * out_h1 * (1 - out_h1) * x2
d_w2 = (d_o1 * out_h1 * (1 - out_h1) * w7 + d_o2 * out_o2 * (1 - out_o2) * w8) * out_h2 * (1 - out_h2) * x1
d_w4 = (d_o1 * out_h1 * (1 - out_h1) * w7 + d_o2 * out_o2 * (1 - out_o2) * w8) * out_h2 * (1 - out_h2) * x2
print("w的梯度:",round(d_w1, 2), round(d_w2, 2), round(d_w3, 2), round(d_w4, 2), round(d_w5, 2), round(d_w6, 2),
round(d_w7, 2), round(d_w8, 2))
return d_w1, d_w2, d_w3, d_w4, d_w5, d_w6, d_w7, d_w8
def update_w(w1, w2, w3, w4, w5, w6, w7, w8):
# 步长
step = 1
w1 = w1 - step * d_w1
w2 = w2 - step * d_w2
w3 = w3 - step * d_w3
w4 = w4 - step * d_w4
w5 = w5 - step * d_w5
w6 = w6 - step * d_w6
w7 = w7 - step * d_w7
w8 = w8 - step * d_w8
return w1, w2, w3, w4, w5, w6, w7, w8
if __name__ == "__main__":
print("权值w0-w7:",round(w1, 2), round(w2, 2), round(w3, 2), round(w4, 2), round(w5, 2), round(w6, 2), round(w7, 2),
round(w8, 2))
for i in range(1):
print("=====第" + str(i+1) + "轮=====")
out_o1, out_o2, out_h1, out_h2 = forward_propagate(x1, x2, y1, y2, w1, w2, w3, w4, w5, w6, w7, w8)
d_w1, d_w2, d_w3, d_w4, d_w5, d_w6, d_w7, d_w8 = back_propagate(out_o1, out_o2, out_h1, out_h2)
w1, w2, w3, w4, w5, w6, w7, w8 = update_w(w1, w2, w3, w4, w5, w6, w7, w8)
print("更新后的权值w:",round(w1, 2), round(w2, 2), round(w3, 2), round(w4, 2), round(w5, 2), round(w6, 2), round(w7, 2),
round(w8, 2))
3. 对比【作业2】与【作业3】的反向传播的实现方法。总结并陈述
【作业2】中反向传播实现的方法为:
-
首先正向传播
计算隐藏层神经元 h 1 h_1 h1 和 h 2 h_2 h2的输入与输出
I n h 1 = w 1 ∗ x 1 + w 3 ∗ x 2 In_{h_{1}} = w_1 * x_1 + w_3 * x_2 Inh1=w1∗x1+w3∗x2 h 1 = O u t h 1 = S i g m o i d ( I n h 1 ) h_1 = Out_{h_1} = Sigmoid(In_{h_1}) h1=Outh1=Sigmoid(Inh1)
I n h 2 = w 2 ∗ x 1 + w 4 ∗ x 2 In_{h_{2}} = w_2 * x_1 + w_4 * x_2 Inh2=w2∗x1+w4∗x2 h 2 = O u t h 2 = S i g m o i d ( I n h 2 ) h_2 = Out_{h_2} = Sigmoid(In_{h_2}) h2=Outh2=Sigmoid(Inh2)
计算输出层 o 1 o_1 o1 和 o 2 o_2 o2的带权输入与输出
I n o 1 = w 5 ∗ h 1 + w 7 ∗ h 2 In_{o_{1}} = w_5 * h_1 + w_7 * h_2 Ino1=w5∗h1+w7∗h2 o 1 = O u t o 1 = S i g m o i d ( I n o 1 ) o_1 = Out_{o_1} = Sigmoid(In_{o_1}) o1=Outo1=Sigmoid(Ino1)
I n o 2 = w 6 ∗ h 1 + w 8 ∗ h 2 In_{o_{2}} = w_6 * h_1 + w_8 * h_2 Ino2=w6∗h1+w8∗h2 o 2 = O u t o 2 = S i g m o i d ( I n o 2 ) o_2 = Out_{o_2} = Sigmoid(In_{o_2}) o2=Outo2=Sigmoid(Ino2)
计算误差:
E r r o r = 1 2 ∑ i = 1 2 ( o i − y i ) 2 Error = \frac {1} {2} \sum_{i = 1}^{2} (o_i - y_i)^2 Error=21i=1∑2(oi−yi)2 -
反向传播
计算梯度:
计算 w 5 w_5 w5到 w 8 w_8 w8的梯度,以 w 5 w_5 w5为例
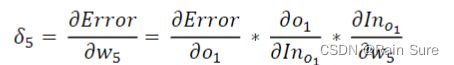
计算 w 1 w_1 w1到 w 4 w_4 w4的梯度,以 w 1 w_1 w1为例
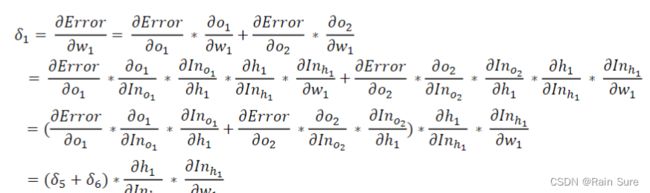
-
更新权值
w i ′ = w i − η ∗ δ i w_i ^{'} = w_i - \eta * \delta_i wi′=wi−η∗δi
【作业3】中反向传播实现的方法:
通过调用现成框架中的函数L.backward()# 自动求梯度,不需要人工编程实现。反向传播,求出计算图中所有梯度存入w中
4. 激活函数Sigmoid使用PyTorch自带函数torch.sigmoid(), 观察,总结。
PyTorch中定义的sigmoid的函数:
![]()
将代码中使用sigmoid函数的部分全部换成使用PyTorch中的sigmoid函数:
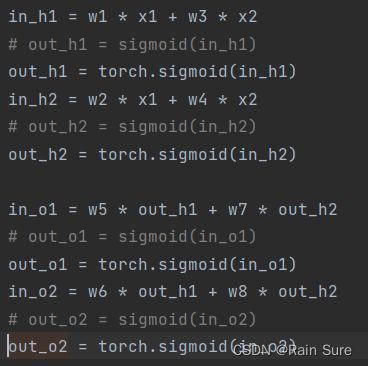
运行结果:
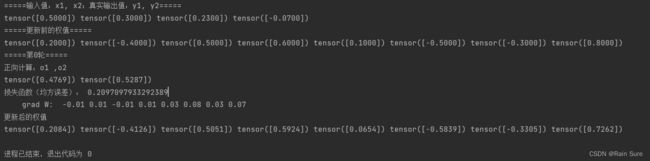
并未看到结果有什么变化啊~ 不太懂,应该没什么区别吧。。。
5. 激活函数Sigmoid改变为Relu,观察、总结并陈述。
将激活函数全部变为Relu,Relu使用PyTorch自带的torch.relu()函数~
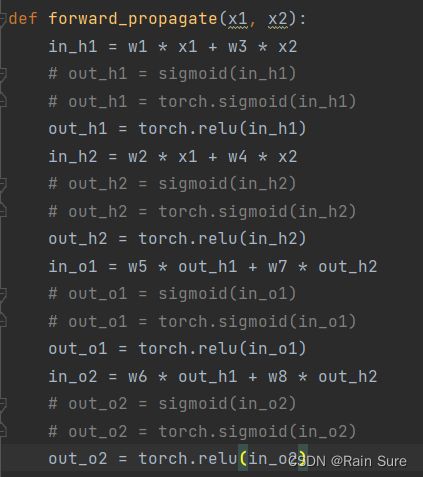
运行结果:
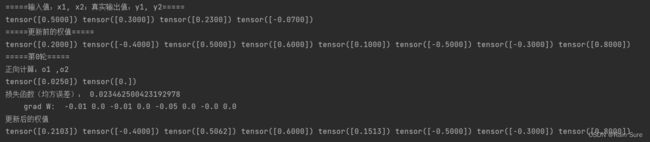
ReLU激活函数是一个简单的计算,如果输入大于0,直接返回作为输入提供的值;如果输入是0或更小,返回值0。
Sigmoid 激活函数需要使用指数计算, 而ReLU只需要max(),因此他计算上更简单,计算成本也更低。
ReLU看起来更像一个线性函数,一般来说,当神经网络的行为是线性或接近线性时,它更容易优化。
这个特性的关键在于,使用这个激活函数进行训练的网络几乎完全避免了梯度消失的问题,因为梯度仍然与节点激活成正比。
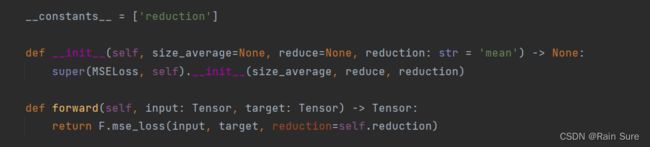
6. 损失函数MSE用PyTorch自带函数 torch.nn.MSELoss()替代,观察、总结并陈述。
torch.nn.MSELoss()核心代码:
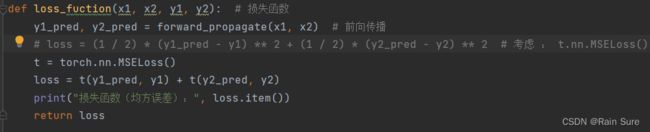
将损失函数替换为torch.nn.MSELoss()函数:
运行结果:
MSE是mean squared error的缩写,即平均平方误差,简称均方误差。
旧版的nn.MSELoss()函数有reduce、size_average两个参数,新版的只有一个reduction参数了,功能是一样的。reduction的意思是维度要不要缩减,以及怎么缩减,有三个选项:
‘none’: no reduction will be applied.
‘mean’: the sum of the output will be divided by the number of elements in the output.
‘sum’: the output will be summed.
如果不设置reduction参数,默认是’mean’。
7. 损失函数MSE改变为交叉熵,观察、总结并陈述。
8. 改变步长,训练次数,观察、总结并陈述。
将步长改为5,训练次数改为10次:

将步长改为10, 训练次数改为100次:

通过运行结果可以看出,训练次数越多,计算结果越准确,精度越高!
9. 权值w1-w8初始值换为随机数,对比【作业2】指定权值结果,观察、总结并陈述
将 w 1 w_1 w1 ~ w 8 w_8 w8全部变为随机数
![]()
训练100次后: 误差变的越来越小了~
交叉熵:


10. 全面总结反向传播原理和编码实现,认真写心得体会
反向传播算法,可以用于优化权值:
主要步骤就是上面所说的那样,说的已经很详细了~
通过不断的将误差后向传播给各个神经元,各个部分分摊误差,然后再进行权值的修正,大概就是这样吧~
经过这两周对反向传播算法的学习,可以说完全理解了反向传播的原理,代码也比较熟悉了,提升了自己对Python的熟练度,还是挺难的!
好好学习,天天向上!
参考资料:
原来ReLU这么好用!一文带你深度了解ReLU激活函数!
pytorch的nn.MSELoss损失函数
反向传播算法详细计算过程与结论公式
torch.nn.CrossEntropyLoss()用法
torch之随机数生成
一文读懂反向传播算法原理