自行车运动学模型Matlab代码实现

openExample('robotics/PlotPathOfAnBicycleKinematicRobotExample')
kinematicModel = bicycleKinematics;
initialState = [0 0 0];
tspan = 0:0.05:1;
inputs = [2 pi/4]; %Turn left
[t,y] = ode45(@(t,y)derivative(kinematicModel,y,inputs),tspan,initialState);
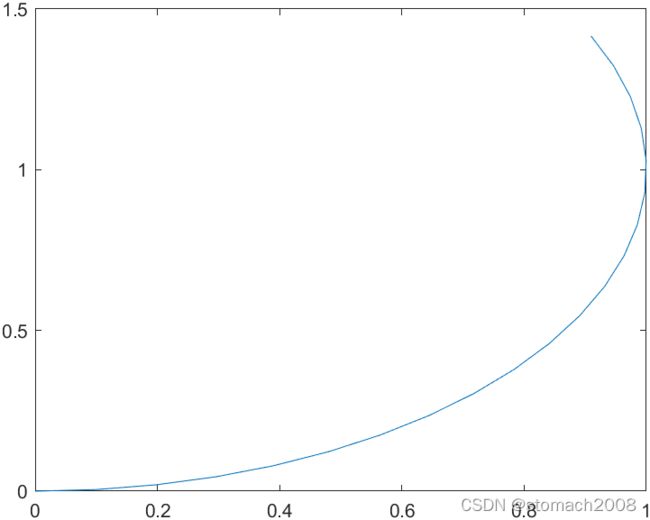
figure
plot(y(:,1),y(:,2))

bicycleKinematics - Bicycle vehicle model

    bicycleKinematics creates a bicycle vehicle model to simulate simplified
    car-like vehicle dynamics.

    kinematicModel = bicycleKinematics
    kinematicModel = bicycleKinematics(Name,Value)

ode45 - 求解非刚性微分方程 - 中阶方法

    此 MATLAB 函数（其中 tspan = [t0 tf]）求微分方程组 y'=f(t,y) 从 t0 到 tf 的积分，初始条件为 y0。解数组 y中的每一行都与列向量 t 中返回的值相对应。

    [t,y] = ode45(odefun,tspan,y0)
    [t,y] = ode45(odefun,tspan,y0,options)
    [t,y,te,ye,ie] = ode45(odefun,tspan,y0,options)
    sol = ode45(___)

bicycleKinematics.derivative - Time derivative of vehicle state

    This MATLAB function returns the current state derivative, stateDot, as a three-element vector [xDot yDot thetaDot] if the motion model is a bicycleKinematics, differentialDriveKinematics, or unicycleKinematics object.

    stateDot = derivative(motionModel,state,cmds)