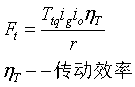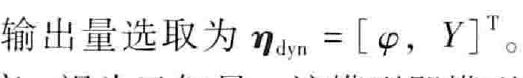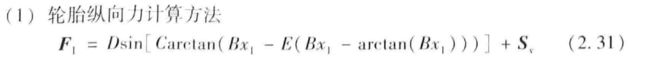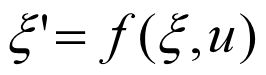车辆运动学模型到动力学模型推导
车辆运动学模型到动力学模型推导
参考 https://www.bilibili.com/video/BV1St411A7nH/?spm_id_from=333.788.recommend_more_video.1
跟着一步步推导,可以清楚的了解车辆动力学模型。
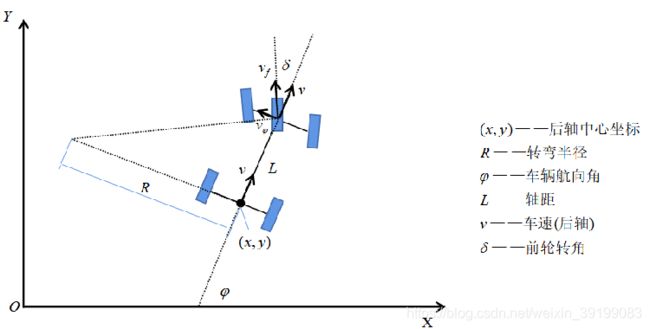
1.车辆运动学模型
车辆运动学模型的推导参见我的另一篇博客 Coursera self-driving car Part1 Final Project——自动驾驶轨迹跟踪之MPC模型预测控制原理推导及Python实现 1.1小节。这里不再赘述
这里的Vr就是后轮车速v
这里的x,y,φ都是大地坐标系,为了和后面推导中的车体坐标系区分,加上下标
为了推导向动力学模型,可以将vr进一步推导,vr由加速度积分得到,加速度又等于F/m,力除以质量
2.动力学模型推导
大地坐标系xg,yg,φg 车体坐标系x,y,φ
2.1 车体-大地坐标系变换
如上图的单轨模型,车体与大地坐标之间存在一个变换关系,具体公式后续推导,先一步步列出思路便于理解。
2.2 车体坐标系下的受力
进一步对车体坐标系下的坐标求导,就是受力分析,横摆较加速度仅与车体的横向受力相关,还有a,b是车子前后轴到质心的距离。
物体在旋转的参考系下平动,有一个科氏力,与平动速度和参考系角速度相关。
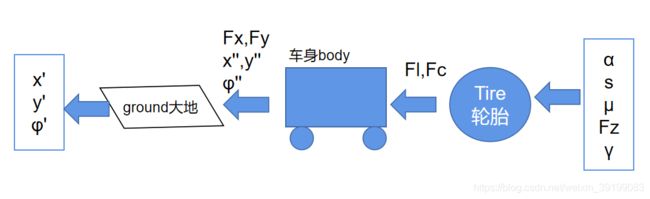
2.3 车轮横纵向受力→车体横纵向受力
2.4 轮胎模型-魔术公式
2.1-2.4就是车辆动力学分析的整个方面,车轮横纵向受力分析→车体横纵向受力分析→求解车体坐标系下横纵向加速度→大地坐标下的横纵向加速度,如下图:
仅考虑xy平面运动
2.5 车辆纵向运动受力分析
由内向外分析,整个传动系 发动机-离合器-变速箱-驱动桥-车轮
假设车子为前置后驱
由上述传动过程可以列出轮胎驱动力Ft的公式如下:
轮胎驱动力就是发动机一路传过来的力矩除以车轮半径乘以个传动效率
根据牛顿第三定律F=ma
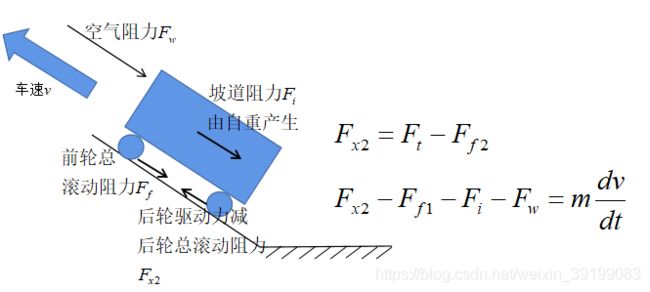
由外向内分析纵向运动受力 假设后驱
传动系是轮胎牵引力Ft的原因,由外向内小车在坡道上这是轮胎力的表现
具体轮胎力从内到外的转化还要分析轮胎的模型。
2.6 轮胎纵向动力学模型
我们要控制2.5中得出公式的Fx2,一个控制发动机输出,一个控制侧偏角,外倾角等在一定范围,控制这些来控制车轮力Fx2
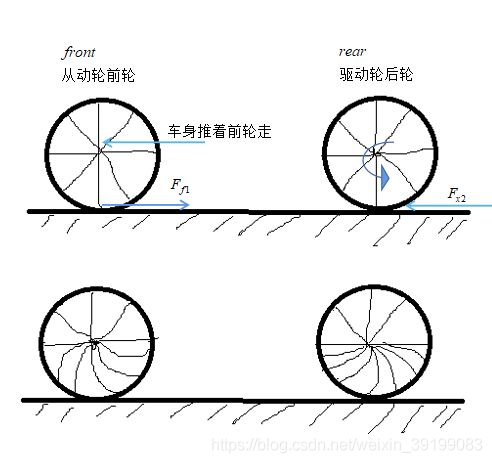
采用刷子模型分析轮胎受力,轮胎看成一条条橡胶条构成,轮胎在与地面接触的地方产生形变。地面只给轮胎摩擦力和竖直方向的力。
上图显示了前后轮的形变示意
前轮摩擦力是阻力,后轮摩擦力是牵引力,是由于橡皮条变形引起的
车子刚运动时,当力矩T不变时,橡皮条变形逐渐增大,牵引力也随橡皮条变形增大而增大,变形到一定程度时橡皮条拉到极限力(弹性极限)不再增大,随后达到平衡,牵引力还有所回落。
滑移:车身速度比轮胎转速快
滑转:车身速度比轮胎转速慢,打滑
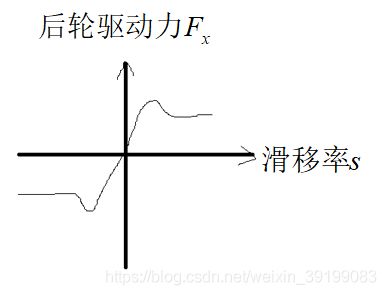
这个纵向动力学的意义就是驱动力矩变成牵引力Fx2的转化关系。跟滑移率是有关系的。
可以看出,在滑移率s比较小时,驱动力Fx和滑移率成近似线性关系。
式中:u为车速; u w为车轮速度;ω为车轮滚动角速度;r为车轮半径。
式写反了,应该是(wr-u)/u,这样打滑时,u很小,wr很大s接近100%
滑移率s定义:轮胎运动中,滑动所占的比例
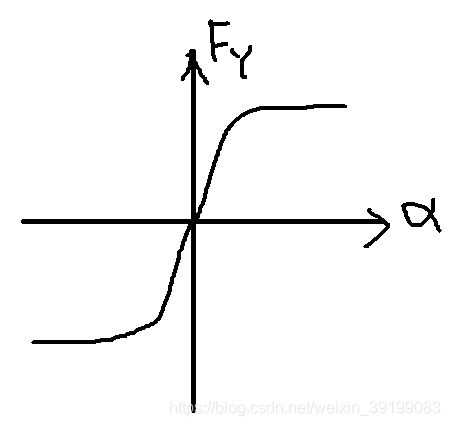
当车轮纯滚动时,u w = u ,s = 0;当车轮抱死纯滑动时, u w = 0 , s =100%;当车轮边滚边滑时,u> uw ,0 和前面2.6节一样,横向力也是因为轮胎的横向变形导致。拐弯时,车子的向心力由地面对轮胎的横向力提供,车子轮胎会产生如上图所示的变形,如果把轮胎看成弹簧或者橡皮条,拐弯时,有甩出去的倾向,轮胎会向左压,它底部被迫向内右变形,底部弹簧产生抵抗力向左,地面对轮胎底部施加一个相反方向即向右的力。 然后取轮宽中心线上的A0,A1,A2,A3,A4, A0最接近变形区,变形量最大,A4变形量最小。当将A0-A4按照变形量投影地面的轨迹上,变形后的轨迹相比无变形的轨迹偏转了一个侧偏角α 此时轮速方向与轴向成一个钝角。 横向力Fy与侧偏角α的关系如下图: 当侧偏角开始增大时,横向力Fy随着侧偏角α的增大而增大,当轮胎达到变形极限时,此时侧偏角再增大,横向力不变 可以看出在小侧偏角α的情况下,横向力Fy与侧偏角α近似成线性关系。 地面摩擦因素和侧倾角是结构性参数是固定的,其他参数是可以控制的。 横向力和纵向力是耦合的,横纵向力的合力不能超过地面所能提供的最大摩擦力μFz 耦合影响如下图: 纵向力曲线和横向力曲线都与垂向载荷Fz有关,Fz越大,越大 本章将给出第二章中受力分析的具体公式 参考 七自由度车辆动力学模型 - 哔哩哔哩专栏 (bilibili.com) 《无人驾驶车辆模型预测控制》 看车辆的单轨模型: 3自由度车辆动力学模型,车辆只有纵向,横向,和横摆运动。 假设车辆前轴两轮的受力相同,后轴两轮的受力也相同。 车辆在纵向,横向,和横摆自由度上的受力方程如下: 科氏力由于车辆在车体坐标x,y方向平动的参考系是车身这个旋转参考系,所以有科氏力。 式中a,b分别位质心到前后轴的距离,m为车辆整备质量,Iz为车辆绕z轴的转动惯量。 科氏力方向的判断:懒得码字直接贴草稿图 轮胎的横纵向力转化成车体坐标下的横纵向力: 轮胎的纵向力横向力与侧偏角,滑移率,路面摩擦系数,垂向载荷有关。 轮胎的侧偏角的计算,用轮胎横向速度/纵向速度的反正切值。 vc和vl可以用vx,vy表示,都是轮胎的速度 滑移率用(轮速-车速)/max(轮速,车速) 式2.10-2.28构成了车辆的动力学模型。 假设车子具有良好的ABS防抱死系统,使得车辆的滑移率始终保持在最佳工作点,摩擦因数μ,滑移率s都视为已知。 选取车体的xy方向速度,横摆角,大地坐标系XY坐标为状态量 控制量为前轮转角,仅考虑前轮转向车子 输出量选为横摆角和XY坐标 4.轮胎模型 轮胎所受的垂直力,横向力,纵向力,和回正力矩对汽车的平顺性,操稳性和安全性起着关键的作用。、魔术公式MF是一个经验轮胎模型,运用三角函数的组合拟合轮胎的实验数据,描述轮胎的纵向力Fl,横向力Fc,回正力矩Mz,翻转力矩Mx,阻力矩My与侧偏角α,滑移率s之间的关系,魔术公式的一般表达式如下: 系数B,C,D由轮胎的垂直载荷和外倾角确定;Y为输出变量可以是Fl/Fc/Mz;x为输入变量,在不同的情况下分别表示轮胎的侧偏角α或纵向滑移率s; B为刚度因子;C为形状因子;D为峰值因子,E为曲率因子 实际应用中侧偏力、滚动阻力会引起偏移,通常还会引入垂直、水平偏移Sv,Sh 将状态方程2.29和魔术公式结合还是过于复杂, 可以注意到侧偏角α较小时,侧向力与侧偏角近似成线性关系;纵向滑移率较小时,纵向力与纵向滑移率近似成线性关系; 在之前建立的车辆动力学非线性模型中,存在较多的三角函数,模型简化困难较大。因此轮胎力的计算过程中提出了小角度的假设 侧偏角可以由车体的x‘,y’,横摆角φ‘计算得到。 小角度假设简化后,上述两式代入下士中前后轮纵横向力 前面介绍了受力分析及推导原理,下面直接给出结果 车辆3自由度动力学模型推导步骤: 1.状态选取x'.y'φ,φ’,X,Y 车体坐标和大地坐标 2.列出x‘’,y‘’,φ‘’受力方程,其中除了状态量还与车轮在车体xy方向的受力Fx,Fy(可坐标变换成车轮横纵向Fl,Fc)有关; 3.Fl,Fc根据小角度假设转化成线性模型,等于刚度乘以滑移率/侧偏角; 4.将滑移率、侧偏角按定义可转化成状态量的表达式,代入Fl,Fc计算式; 5.将Fl,Fc的用状态量计算的表达式代入x,y,φ受力方程,再加上车体坐标和大地坐标的变换关系,联立就得到车辆的动力学模型。 上述草稿最后的状态方程有错误,因为x'出现在等式右边的分母上,是非线性模型,而不是线性时变模型。要通过局部泰勒展开,局部线性近似才行。状态方程可以在参考状态泰勒展开,然后与参考状态表达式做差即可线性化。 2.7轮胎横向动力学模型
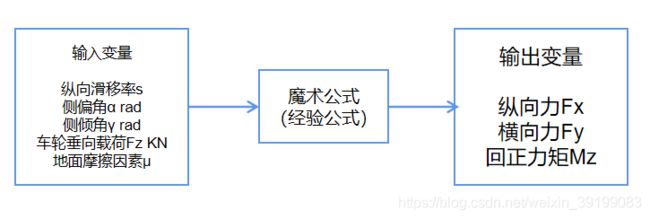
2.8 轮胎模型的输入输出
3.车辆动力学模型公式
![]()
5.小角度假设下的车辆动力学模型
6 动力学模型结果