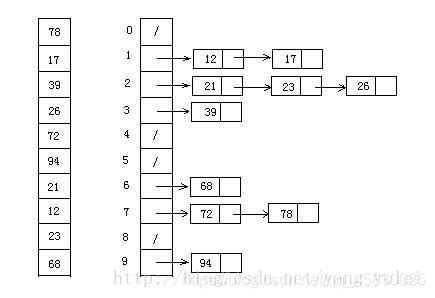
十大排序讲解(算法思想+动图演示+算法实现(模板代码))

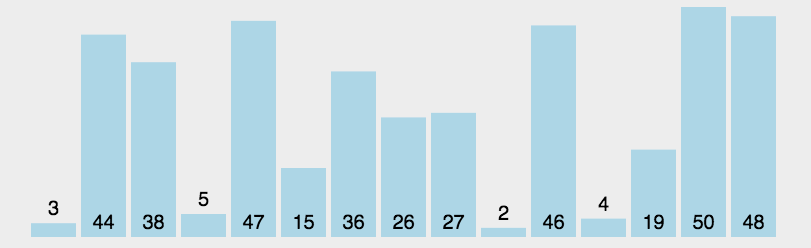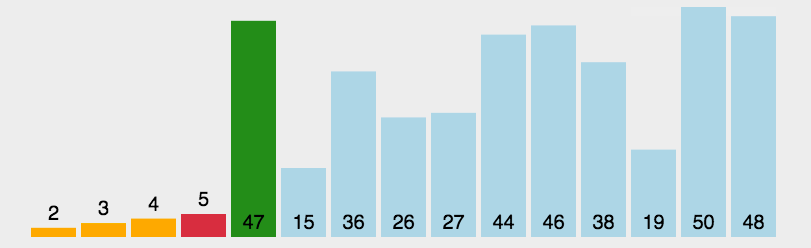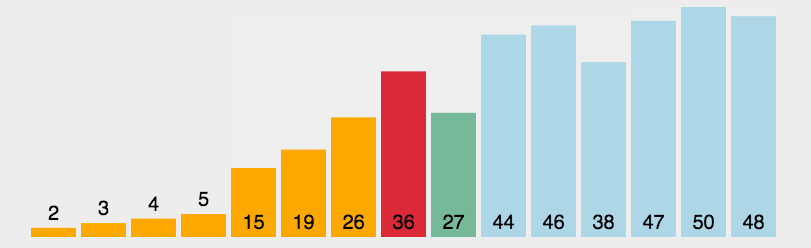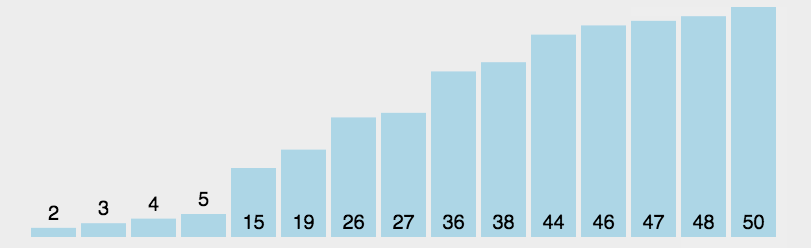
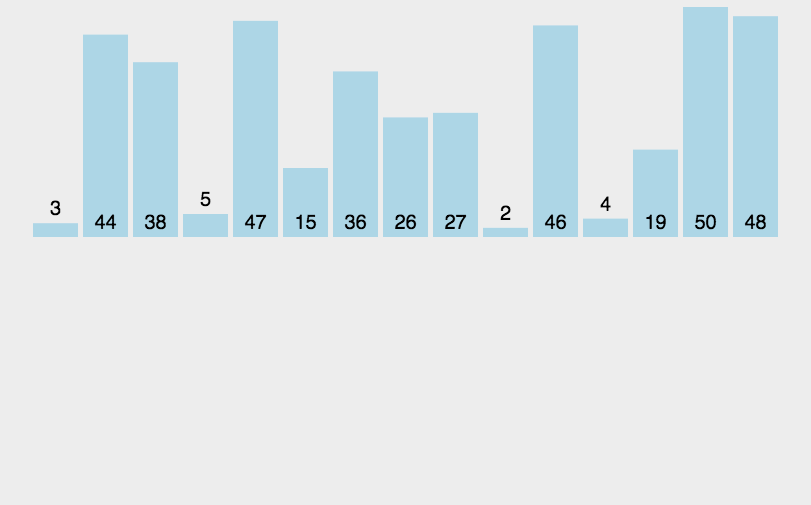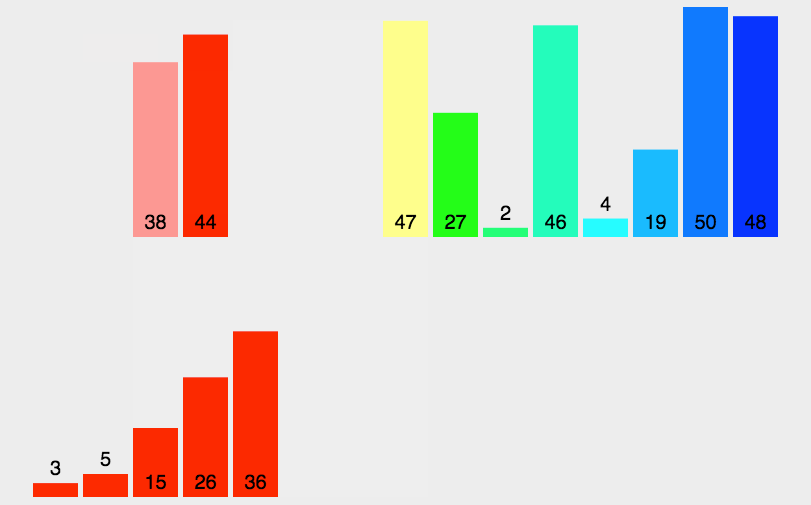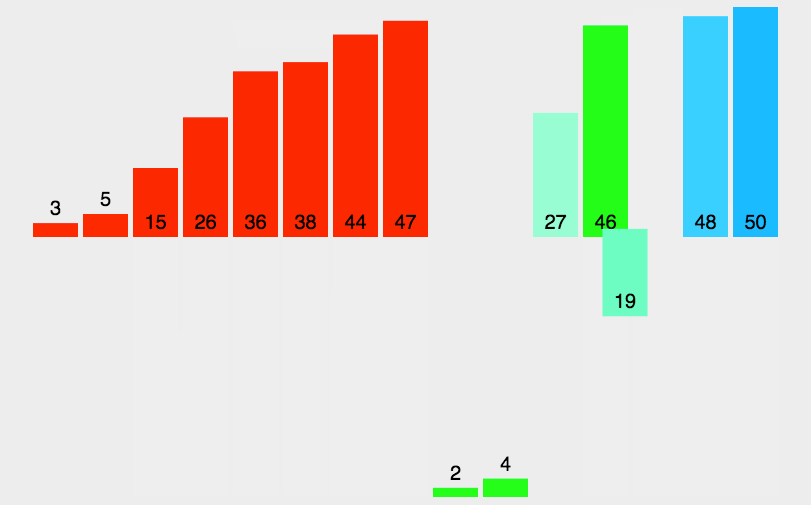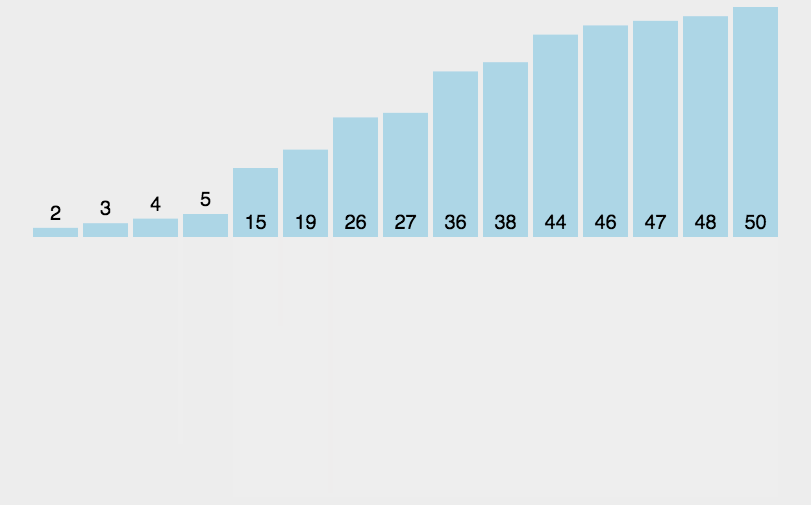
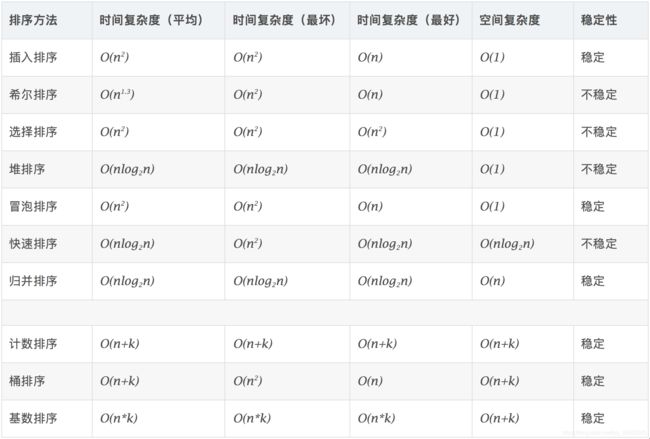
首先，让我们来看看其他博主整理的图片：
（初步感受一下这八种排序的比较）

1.插入排序（InsertSort）

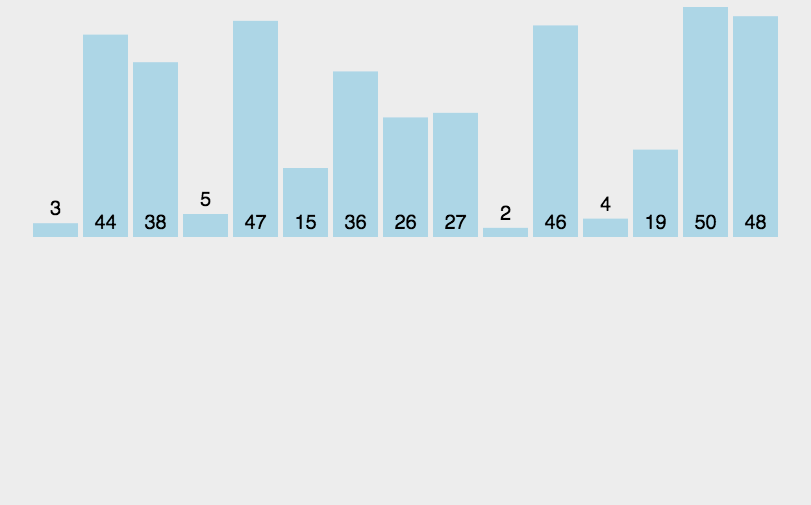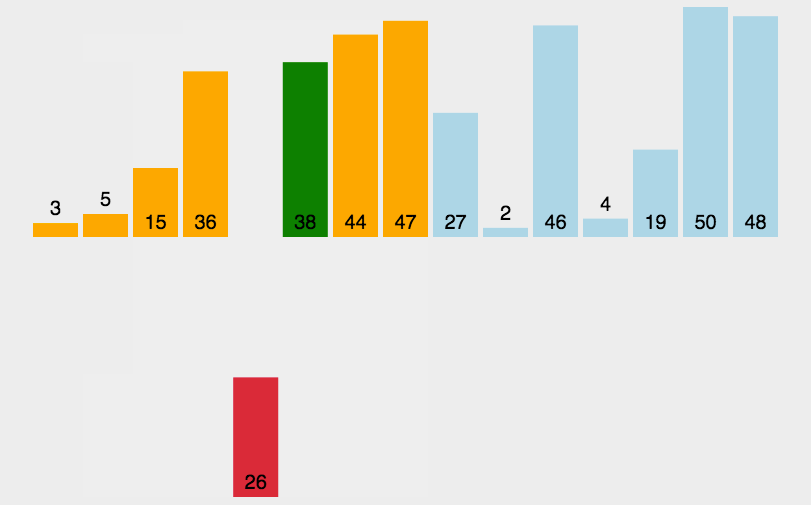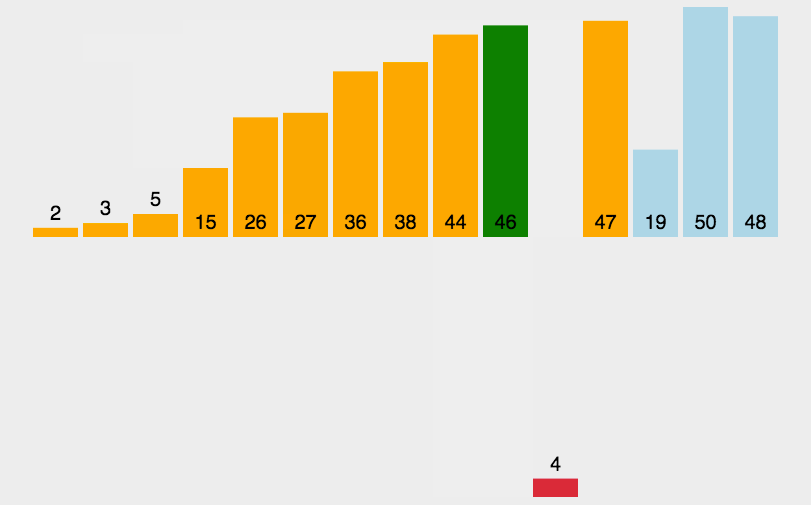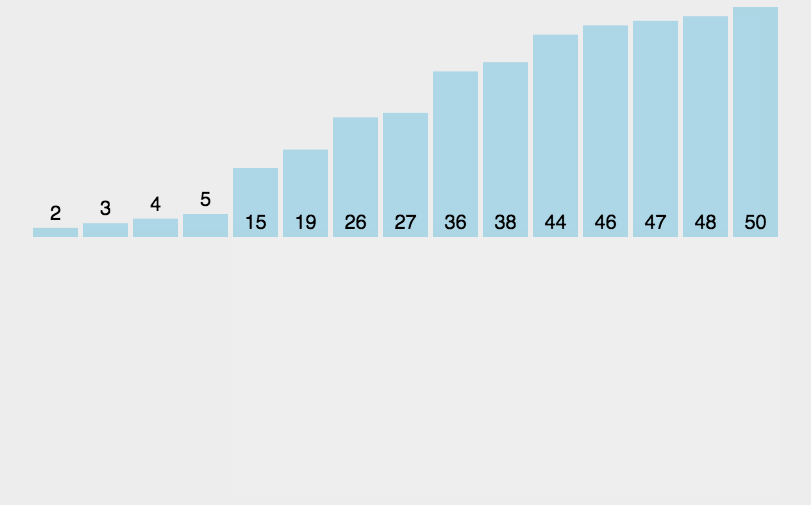
算法思想

插入排序从第二个数开始，拿出第二个数进行向前插入排序，一直到最后一个数向前做插入排序。算法稳定。

时间复杂度: O($n^2$):
空间复杂度为:O(1)
最好的时间复杂度是O(n)
最坏也就是平均是O($n^2$)

算法实现

/**
    * 插入排序
    * 1、确定插入排序的数，从第二个开始选择
    * 2、选择插入排序的数，保存为num
    * 3、计算num前一个数的索引
    * 4、进行检查，如果num小于前面的数，则将前一个数往后移，若比前一个数大，则结束此次循环
    * 5、结束时的位置保存num
    */

void Insert_sort(int *dp)
{
    for(int i=1; i<dp.length; i++) //从第二个值开始
    {
        //用num存选择插入排序的数
        int num=dp[i];
        //计算num前一个数的索引(下标)
        int pos=i-1;
        for(; pos>=0; pos--)
        {
            //依次向前遍历进行判断num和前一个数的大小
            //如果num小于前面的数，则将前一个数往后移
            //如果num大于前面的数，则结束循环
            if(num<dp[pos])
                dp[pos+1]=dp[pos];
            else
                break;
        }
        //保存num的值
        if(num!=dp[i])
        {
            dp[pos+1]=num;
        }
    }
}

2.希尔排序(ShellSort)

算法思想

希尔算法又名缩小增量排序，本质是插入排序，只不过是将待排序的序列按某种规则分成几个子序列，分别对几个子序列进行直接插入排序。这个规则就是增量，增量选取很重要，增量一般选序列长度一半，然后逐半递减，直到最后一个增量为1，为1相当于直接插入排序。

算法时间复杂度：
最好情况：当数据已经排好序的情况下：O($N^{1.3}$)；
最坏情况：O($N^2$)；
平均情况：O($nlogn$)
算法空间复杂度：O(1)
算法稳定性：不稳定

算法实现

void Shell_sort(int *dp,int group)
{
    //初始步长设为group
    //然后依次减半，直到最后取1
    for(int k=group; k>=1;)
    {
        //组内排序
        for(int i=k; i<dp.length; i++)
        {
            if(dp[i]<dp[i-k])
            {
                int pos=dp[i];
                for(int j=i-k; j>=0&&dp[j]>pos; j-=k)
                {
                    dp[j+k]=dp[j];
                }
                dp[j+k]=pos;
            }
        }
        //修正步长
        if(k>1)
            k = (k+1)/2;
        else if(k==1)
            break;
    }
}

3.冒泡排序（Bubble Sort）

算法思想

1. 比较相邻的元素。如果第一个比第二个大，就交换它们两个；
2. 对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对，这样在最后的元素应该会是最大的数；
3. 针对所有的元素重复以上的步骤，除了最后一个
4. 重复步骤1~3，直到排序完成。

算法实现

void Bubble_sort(int *dp)
{
    //控制比较轮数
    for(int i=1;i<dp.length;i++)
    {
        //控制每轮比较次数
        for(int j=0;j<dp.length-i;j++)
        {
            if(dp[j]>dp[j+1])
            {
                int temp=dp[j];
                dp[j]=dp[j+1];
                dp[j+1]=temp;
            }
        }
    }
}

4.快速排序(Quicksort)

算法思想

快速排序其实是在冒泡排序的基础上做出的一个改进.

快速排序算法利用的是一趟快速排序,基本内容是选择一个数作为准基数,然后利用这个准基数将遗传数据分为两个部分,第一部分比这个准基数小,都放在准基数的左边,第二部分都比这个准基数大,放在准基数的右边.

接下来这两部分都是用快排(可以使用递归的方法)完成从小到大的排序.

冒泡排序的原理：从第一个数开始，依次往后比较，如果前面的数比后面的数大就交换，否则不作处理。这就类似烧开水时，壶底的水泡往上冒的过程。

算法实现

void Quick_sort(int *dp, int l, int r)  // l,r为左右边界
{
    int i = l;
    int j = r;
    int mid = dp[l];
    if (i >= j) return;
    while (i < j) {
        while (i < j && dp[j] >= mid) j--;
        dp[i] = dp[j];
        while (i < j && dp[i] <= mid) i++;
        dp[j] = dp[i];
    }
    dp[i] = mid;
    Quick_sort(dp,l, i - 1);  //递归左边
    Quick_sort(dp,i + 1, r);  //递归右边
}

5.选择排序(Selection-sort)

算法思想

选择排序(Selection-sort)是一种简单直观的排序算法。它的工作原理：首先在未排序序列中找到最小（大）元素，存放到排序序列的起始位置，然后，再从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾。以此类推，直到所有元素均排序完毕。

n个记录的直接选择排序可经过n-1趟直接选择排序得到有序结果。具体算法描述如下：

• 初始状态：无序区为R[1…n]，有序区为空；
• 第i趟排序(i=1,2,3…n-1)开始时，当前有序区和无序区分别为R[1…i-1]和R(i…n）。该趟排序从当前无序区中-选出关键字最小的记录
• R[k]，将它与无序区的第1个记录R交换，使R[1…i]和R[i+1…n)分别变为记录个数增加1个的新有序区和记录个数减少1个的新无序区；
• n-1趟结束，数组有序化了。

算法实现

void Select_sort(int *dp,int len)
{
    //len为数组长度
    int minn = 0;
    int temp = 0;
    for (int i =0; i<len-1; i++)
    {
        minn = i;
        for (int j=i; j<len; j++)
        {
            if (dp[j]<dp[minn])
            {
                minn = j;
            }
        }
        if (i != minn)
        {
            temp = dp[minn];
            dp[minn] = dp[i];
            dp[i] = temp;
        }
    }
}

6.堆排序(Heapsort)

算法思想

堆排序（Heapsort）是指利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构，并同时满足堆积的性质：即子结点的键值或索引总是小于（或者大于）它的父节点。

• 将初始待排序关键字序列$(R_1,R_2\dots .R_n)$构建成大顶堆，此堆为初始的无序区；

• 将堆顶元素R[1]与最后一个元素R[n]交换，此时得到新的无序区$(R_1,R_2\dots .R_{n-1})$和新的有序区(Rn),且满足R[1,2…n-1]<=R[n]；

• 由于交换后新的堆顶R[1]可能违反堆的性质，因此需要对当前无序区$(R_1,R_2\dots .R_{n-1})$调整为新堆，然后再次将R[1]与无序区最后一个元素交换，得到新的无序区$(R_1,R_2\dots .R_{n-2})$和新的有序区($R_{n-1},R_n$)。不断重复此过程直到有序区的元素个数为n-1，则整个排序过程完成。
  

算法实现

void swap(int array[], int x, int y) {
    int key  = array[x];
    array[x] = array[y];
    array[y] = key;
}

// 从大到小排序
// void Down(int array[], int i, int n) {
//     int child = 2 * i + 1;
//     int key   = array[i];
//     while (child < n) {
//         if (array[child] > array[child + 1] && child + 1 < n) {
//             child++;
//         }
//         if (key > array[child]) {
//             swap(array, i, child);
//             i = child;
//         } else {
//             break;
//         }
//         child = child * 2 + 1;
//     }
// }

// 从小到大排序
void Down(int array[], int i, int n) { // 最后结果就是大顶堆
    int parent = i;                    // 父节点下标
    int child  = 2 * i + 1;            // 子节点下标
    while (child < n) {
        if (array[child] < array[child + 1] && child + 1 < n) { // 判断子节点那个大，大的与父节点比较
            child++;
        }
        if (array[parent] < array[child]) { // 判断父节点是否小于子节点
            swap(array, parent, child);     // 交换父节点和子节点
            parent = child;                 // 子节点下标 赋给 父节点下标
        }
        child = child * 2 + 1; // 换行，比较下面的父节点和子节点
    }
}

void BuildHeap(int array[], int size) {
    for (int i = size / 2 - 1; i >= 0; i--) { // 倒数第二排开始, 创建大顶堆，必须从下往上比较
        Down(array, i, size);                 // 否则有的不符合大顶堆定义
    }
}

void HeapSort(int array[], int size) {
    printf("初始化数组：");
    BuildHeap(array, size); // 初始化堆
    display(array, size);   // 查看初始化结果
    for (int i = size - 1; i > 0; i--) {
        swap(array, 0, i); // 交换顶点和第 i 个数据
                           // 因为只有array[0]改变，其它都符合大顶堆的定义，所以可以从上往下重新建立
        Down(array, 0, i); // 重新建立大顶堆

        printf("排序的数组：");
        display(array, size);
    }
}

7.归并排序（Merge Sort）

算法描述

归并排序是建立在归并操作上的一种有效的排序算法。该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为2-路归并。

• 把长度为n的输入序列分成两个长度为n/2的子序列；
• 对这两个子序列分别采用归并排序；
• 将两个排序好的子序列合并成一个最终的排序序列
  

算法实现

/*
往mp中放入元素，并且实时更新dp数组中的元素顺序
把通过用归并排序排好的元素先放进mp中，
然后再用mp给dp赋值，这样对dp数组进行更新;
*/
void Merge(int l1,int r1,int l2,int r2)
{
    int pos=0;
    int pos1=l1;
    int pos2=l2;
    while(pos1<=r1&&pos2<=r2)
    {
        if(dp[pos1]<=dp[pos2])
            mp[pos++]=dp[pos1++];
        else
            mp[pos++]=dp[pos2++];
    }
    //如果mid前面的元素数目比mid后面的元素数目少，那么后面就剩下了很多的元素；
    while(pos1<=r1)
        mp[pos++]=dp[pos1++];  //把后面余下的mid前面元素放进mp中;
    while(pos2<=r2)
        mp[pos++]=dp[pos2++];  //把后面余下的mid后面元素放进mp中;
    for(int i=l1; i<=r2; i++)
        dp[i]=mp[i-l1];  //用mp数组对dp数组进行更新;
}

void Merge_sort(int l,int r)
{
    int mid;
    if(l<r)
    {
        mid=(l+r)/2;
        Merge_sort(l,mid);  //左边递归到最小；
        Merge_sort(mid+1,r);  //右边递归到最小；
        Merge(l,mid,mid+1,r);
    }
}

8.基数排序（Radix Sort）

算法思想

基数排序是按照低位先排序，然后收集；再按照高位排序，然后再收集；依次类推，直到最高位。有时候有些属性是有优先级顺序的，先按低优先级排序，再按高优先级排序。最后的次序就是高优先级高的在前，高优先级相同的低优先级高的在前。

• 取得数组中的最大数，并取得位数；
• arr为原始数组，从最低位开始取每个位组成radix数组；
• 对radix进行计数排序（利用计数排序适用于小范围数的特点）；
  

算法实现

/*
*求数据的最大位数,决定排序次数
*/
int maxbit(int data[], int n) 
{
    int d = 1; //保存最大的位数
    int p = 10;
    for(int i = 0; i < n; ++i)
    {
        while(data[i] >= p)
        {
            p *= 10;
            ++d;
        }
    }
    return d;
}
void radixsort(int data[], int n) //基数排序
{
    int d = maxbit(data, n);
    int tmp[n];
    int count[10]; //计数器
    int i, j, k;
    int radix = 1;
    for(i = 1; i <= d; i++) //进行d次排序
    {
        for(j = 0; j < 10; j++)
            count[j] = 0; //每次分配前清空计数器
        for(j = 0; j < n; j++)
        {
            k = (data[j] / radix) % 10; //统计每个桶中的记录数
            count[k]++;
        }
        for(j = 1; j < 10; j++)
            count[j] = count[j - 1] + count[j]; //将tmp中的位置依次分配给每个桶
        for(j = n - 1; j >= 0; j--) //将所有桶中记录依次收集到tmp中
        {
            k = (data[j] / radix) % 10;
            tmp[count[k] - 1] = data[j];
            count[k]--;
        }
        for(j = 0; j < n; j++) //将临时数组的内容复制到data中
            data[j] = tmp[j];
        radix = radix * 10;
    }
}

9.计数排序（Counting Sort）

算法描述

计数排序不是基于比较的排序算法，其核心在于将输入的数据值转化为键存储在额外开辟的数组空间中。 作为一种线性时间复杂度的排序，计数排序要求输入的数据必须是有确定范围的整数。

• 找出待排序的数组中最大和最小的元素；
• 统计数组中每个值为i的元素出现的次数，存入数组C的第i项；
• 对所有的计数累加（从C中的第一个元素开始，每一项和前一项相加）；
• 反向填充目标数组：将每个元素i放在新数组的第C(i)项，每放一个元素就将C(i)减去1。
  

算法实现

void Counting_sort(int *dp, int n)
{
    int mp[111];  //桶
    memset(mp,0,sizeof(mp));　//清空桶
    int maxn;  //假设maxn为dp数组中的最大值
    int i;
    for(i=0;i<n;i++)
    {
        mp[dp[i]]++;  //对应桶＋＋
    }
    for(i=0;i<=maxn;i++)
    {
        cout<<mp[i]<<endl;
    }
    
}
    

10.桶排序（Bucket Sort）

算法描述

排序是计数排序的升级版。它利用了函数的映射关系，高效与否的关键就在于这个映射函数的确定。桶排序 (Bucket sort)的工作的原理：假设输入数据服从均匀分布，将数据分到有限数量的桶里，每个桶再分别排序（有可能再使用别的排序算法或是以递归方式继续使用桶排序进行排）。

• 设置一个定量的数组当作空桶；
• 遍历输入数据，并且把数据一个一个放到对应的桶里去；
• 对每个不是空的桶进行排序；
• 从不是空的桶里把排好序的数据拼接起来。
  

算法实现

void Bucket_sort(int *dp,int num)
{
    int a[11];
    for(int i=0;i<=10;i++)
        a[i]=0;

    for(int i=0;i<num;i++)
    {
        int temp=dp[i];
        ++a[temp];
    }

    for(int i=0;i<11;i++)
    {
        int num_print=a[i];
        for(int j=1;j<=num_print;j++)
           cout<<i<<" ";
    }
}