【李沐：动手学深度学习pytorch版】第3章：线性神经网络

第3章 线性神经网络

3.1. 线性回归

3.1.1. 线性回归的基本元素

3.1.1.1. 线性模型

3.1.1.2. 损失函数

3.1.1.3. 解析解

线性回归刚好是一个很简单的优化问题。 与我们将在本书中所讲到的其他大部分模型不同，线性回归的解可以用一个公式简单地表达出来， 这类解叫作解析解（analytical solution）。

3.1.1.4. 随机梯度下降

即使在我们无法得到解析解的情况下，我们仍然可以有效地训练模型。 在许多任务上，那些难以优化的模型效果要更好。 因此，弄清楚如何训练这些难以优化的模型是非常重要的。

本书中我们用到一种名为梯度下降（gradient descent）的方法， 这种方法几乎可以优化所有深度学习模型。 它通过不断地在损失函数递减的方向上更新参数来降低误差。

梯度下降最简单的用法是计算损失函数（数据集中所有样本的损失均值） 关于模型参数的导数（在这里也可以称为梯度）。 但实际中的执行可能会非常慢：因为在每一次更新参数之前，我们必须遍历整个数据集。 因此，我们通常会在每次需要计算更新的时候随机抽取一小批样本， 这种变体叫做小批量随机梯度下降（minibatch stochastic gradient descent）。

批量大小和学习率的值通常是手动预先指定，而不是通过模型训练得到的。 这些可以调整但不在训练过程中更新的参数称为超参数（hyperparameter）。

调参（hyperparameter tuning）是选择超参数的过程。 超参数通常是我们根据训练迭代结果来调整的， 而训练迭代结果是在独立的验证数据集（validation dataset）上评估得到的。

3.1.2. 矢量化加速

在训练我们的模型时，我们经常希望能够同时处理整个小批量的样本。 为了实现这一点，需要我们对计算进行矢量化， 从而利用线性代数库，而不是在Python中编写开销高昂的for循环。

%matplotlib inline
import math
import time
import numpy as np
import torch
from d2l import torch as d2l

n = 10000
a = torch.ones(n)
b = torch.ones(n)

由于在本书中我们将频繁地进行运行时间的基准测试，所以我们定义一个计时器：

class Timer:  #@save
    """记录多次运行时间"""
    def __init__(self):
        self.times = []
        self.start()

    def start(self):
        """启动计时器"""
        self.tik = time.time()

    def stop(self):
        """停止计时器并将时间记录在列表中"""
        self.times.append(time.time() - self.tik)
        return self.times[-1]

    def avg(self):
        """返回平均时间"""
        return sum(self.times) / len(self.times)

    def sum(self):
        """返回时间总和"""
        return sum(self.times)

    def cumsum(self):
        """返回累计时间"""
        return np.array(self.times).cumsum().tolist()

为了说明矢量化为什么如此重要，我们考虑对向量相加的两种方法。 我们实例化两个全为1的10000维向量。

在一种方法中，我们将使用Python的for循环遍历向量； 在另一种方法中，我们将依赖对+的调用。

c = torch.zeros(n)
timer = Timer()
for i in range(n):
    c[i] = a[i] + b[i]
f'{timer.stop():.5f} sec'

'0.08062 sec'

或者，我们使用重载的+运算符来计算按元素的和。

timer.start()
d = a + b
f'{timer.stop():.5f} sec'

'0.00000 sec'

结果很明显，第二种方法比第一种方法快得多。 矢量化代码通常会带来数量级的加速。

3.1.3. 正态分布与平方损失

定义一个Python函数来计算正态分布。

def normal(x, mu, sigma):
    p = 1 / math.sqrt(2 * math.pi * sigma**2)
    return p * np.exp(-0.5 / sigma**2 * (x - mu)**2)

我们现在可视化正态分布。

# 再次使用numpy进行可视化
x = np.arange(-7, 7, 0.01)

# 均值和标准差对
params = [(0, 1), (0, 2), (3, 1)]
d2l.plot(x, [normal(x, mu, sigma) for mu, sigma in params], 
         xlabel='x', ylabel='p(x)', figsize=(4.5, 2.5), legend=[f'mean {mu}, std {sigma}' for mu, sigma in params])

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-vjLt1hSL-1640697552260)(https://gitee.com/zdbya/picgo_image/raw/master/SSL_img/202112282117668.svg+xml)]

3.2 线性回归的从零开始实现

%matplotlib inline
import random
import torch
from d2l import torch as d2l

3.2.1. 生成数据集

def synthetic_data(w, b, num_examples):  #@save
    """生成y=Xw+b+噪声"""
    X = torch.normal(0, 1, (num_examples, len(w)))  #生成均值为0，方差为1的随机数，size：n个样本*w的长度
    y = torch.matmul(X, w) + b
    y += torch.normal(0, 0.01, y.shape)             #加噪音
    return X, y.reshape((-1, 1))                   #y做成列向量返回

# 定义真实的w和b
true_w = torch.tensor([2, -3.4])
true_b = 4.2

# 生成特征和标注
features, labels = synthetic_data(true_w, true_b, 1000)

print(features[:5])
print(labels[:5])

tensor([[-0.0121, -0.3654],
        [-0.1914, -0.8442],
        [ 2.0900,  1.2727],
        [ 1.7094, -0.0526],
        [-0.6532,  0.5247]])
tensor([[5.4116],
        [6.6812],
        [4.0552],
        [7.7907],
        [1.1062]])

注意，features中的每一行都包含一个二维数据样本， labels中的每一行都包含一维标签值（一个标量）。

print('features:', features[0],'\nlabel:', labels[0]) #输出第0个样本的信息

features: tensor([-0.0121, -0.3654]) 
label: tensor([5.4116])

通过生成第二个特征features[:, 1]和labels的散点图， 可以直观观察到两者之间的线性关系。

d2l.set_figsize()
d2l.plt.scatter(features[:, 1].detach().numpy(), labels.detach().numpy(), 1);

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-LZtBxndx-1640697552261)(https://gitee.com/zdbya/picgo_image/raw/master/SSL_img/202112282117333.svg+xml)]

3.2.2 读取数据集

回想一下，训练模型时要对数据集进行遍历，每次抽取一小批量样本，并使用它们来更新我们的模型。 由于这个过程是训练机器学习算法的基础，所以有必要定义一个函数， 该函数能打乱数据集中的样本并以小批量方式获取数据。

在下面的代码中，我们定义一个data_iter函数， 该函数接收批量大小、特征矩阵和标签向量作为输入，生成大小为batch_size的小批量。 每个小批量包含一组特征和标签。

# 读取小批量
def data_iter(batch_size, features, labels):
    num_examples = len(labels)
    
    indices = list(range(num_examples))  # 生成每个样本的index
    # 这些样本是随机读取的，没有特定的顺序
    random.shuffle(indices)
    
    for i in range(0, num_examples, batch_size):  # batch_size步长
        batch_indices = torch.tensor(indices[i : min(i+batch_size, num_examples)])
        
        yield features[batch_indices], labels[batch_indices]

每次随机选取10个样本参与计算

batch_size = 10

for X, y in data_iter(batch_size, features, labels):
    print(X, '\n', y)
    break

tensor([[ 0.4074, -0.8667],
        [ 0.2685, -1.4512],
        [ 0.4134,  0.5147],
        [ 2.1151,  0.2318],
        [-0.0404, -0.1825],
        [-0.0340,  0.8932],
        [ 0.2615,  0.3789],
        [-0.0181,  1.2089],
        [-0.2787, -0.2607],
        [-0.2790,  0.2957]]) 
 tensor([[7.9558],
        [9.6703],
        [3.3044],
        [7.6358],
        [4.7363],
        [1.0928],
        [3.4373],
        [0.0567],
        [4.5363],
        [2.6374]])

3.2.3. 初始化模型参数

#w，b需要计算梯度
w = torch.normal(0, 0.01, size=(2,1), requires_grad=True)  #w是长为2的向量
print(w)
b = torch.zeros(1, requires_grad=True)

tensor([[-0.0079],
        [-0.0156]], requires_grad=True)

3.2.4. 定义模型

def linreg(X, w, b):  #@save
    """线性回归模型"""
    return torch.matmul(X, w) + b

X维度：(样本个数,2)
w维度：(2,1)
b为标量，这里用到广播机制
返回结果维度：(样本个数，1)

3.2.5. 定义损失函数

def squared_loss(y_hat, y):  #y_hat为预测值，y为真实值
    """均方损失"""
    return (y_hat - y.reshape(y_hat.shape)) ** 2 / 2

3.2.6. 定义优化算法

梯度下降

因为我们计算的损失是一个批量样本的总和，所以我们用批量大小（batch_size） 来规范化步长，这样步长大小就不会取决于我们对批量大小的选择。

def sgd(params, lr, batch_size):  #所有参数w,b 学习率  batch_size
    """小批量随机梯度下降"""
    with torch.no_grad():                              #更新的时候不需要计算梯度
        for param in params:                          # 每一个参数，可能是w，可能是b
            param -= lr * param.grad / batch_size     # 梯度下降，所以减去
            param.grad.zero_()                        # 梯度设成0，方便下一次梯度计算 不累加梯度

3.2.7. 训练

这里的迭代周期个数num_epochs和学习率lr都是超参数，分别设为3和0.03。 设置超参数很棘手，需要通过反复试验进行调整

lr = 0.03
num_epochs = 3        # 整个数据扫三遍
net = linreg          # 模型
loss = squared_loss   # 均方损失

for epoch in range(num_epochs):
    for X, y in data_iter(batch_size, features, labels):
        l = loss(net(X, w, b), y)  # X和y的小批量损失
        # 因为l形状是(batch_size,1)，而不是一个标量。l中的所有元素被加到一起，
        # 并以此计算关于[w,b]的梯度
        l.sum().backward()
        sgd([w, b], lr, batch_size)  # 使用参数的梯度更新参数
        
    #print(net(features, w, b).shape, labels.shape)
    with torch.no_grad():  #把不需要计算梯度的代码放里面
        train_l = loss(net(features, w, b), labels)
        print(f'epoch {epoch + 1}, loss {float(train_l.mean()):f}')

epoch 1, loss 0.000050
epoch 2, loss 0.000050
epoch 3, loss 0.000050

print(f'w的估计误差: {true_w - w.reshape(true_w.shape)}')
print(f'b的估计误差: {true_b - b}')

w的估计误差: tensor([ 0.0008, -0.0009], grad_fn=)
b的估计误差: tensor([0.0004], grad_fn=)

3.3. 线性回归的简洁实现

3.3.1. 生成数据集

import numpy as np
import torch
from torch.utils import data
from d2l import torch as d2l

true_w = torch.tensor([2, -3.4])
true_b = 4.2
features, labels = d2l.synthetic_data(true_w, true_b, 1000)

features[:5], labels[:5]

(tensor([[ 1.6126, -0.3805],
         [-1.4653,  1.5517],
         [-0.3078, -0.1138],
         [-2.2826,  1.4290],
         [ 0.1115, -1.7052]]),
 tensor([[ 8.7295],
         [-4.0137],
         [ 3.9659],
         [-5.2199],
         [10.2216]]))

3.3.2. 读取数据集

我们可以调用框架中现有的API来读取数据。 我们将features和labels作为API的参数传递，并通过数据迭代器指定batch_size。 此外，布尔值is_train表示是否希望数据迭代器对象在每个迭代周期内打乱数据

def load_array(data_arrays, batch_size, is_train=True):  #@save
    """构造一个PyTorch数据迭代器"""
    dataset = data.TensorDataset(*data_arrays)
    return data.DataLoader(dataset, batch_size, shuffle=is_train)  # 每次随机挑选

batch_size = 10   # 每次从样本中随机采样十个
data_iter = load_array((features, labels), batch_size)

next(iter(data_iter))

[tensor([[ 0.0539,  2.2867],
         [-0.4324, -1.5015],
         [-1.2343,  0.1497],
         [-0.5834, -0.2978],
         [ 0.2663, -0.6757],
         [-0.6002, -0.3529],
         [-1.7964, -0.1168],
         [ 0.3740, -0.1144],
         [-0.1221,  1.1180],
         [-0.2655,  1.1593]]),
 tensor([[-3.4808],
         [ 8.4551],
         [ 1.2200],
         [ 4.0385],
         [ 7.0235],
         [ 4.1996],
         [ 1.0143],
         [ 5.3379],
         [ 0.1421],
         [-0.2705]])]

3.3.3. 定义模型

Sequential类将多个层串联在一起。
当给定输入数据时，Sequential实例将数据传入到第一层， 然后将第一层的输出作为第二层的输入，以此类推。

Sequential类将多个层串联在一起。 当给定输入数据时，Sequential实例将数据传入到第一层， 然后将第一层的输出作为第二层的输入，以此类推。

# nn是神经网络的缩写
from torch import nn

net = nn.Sequential(nn.Linear(2, 1))  #指定输入输出维度   

3.3.4. 初始化模型参数

在使用net之前，我们需要初始化模型参数。
如在线性回归模型中的权重和偏置。
在这里，我们指定每个权重参数应该从均值为0、标准差为0.01的正态分布中随机采样， 偏置参数将初始化为零。

我们通过net[0]选择网络中的第一个图层， 然后使用weight.data和bias.data方法访问参数。
我们还可以使用替换方法normal_和fill_来重写参数值。

net[0].weight.data.normal_(0, 0.01)
net[0].bias.data.fill_(0)

tensor([0.])

3.3.5. 定义损失函数

计算均方误差使用的是MSELoss类，也称为平方 L2 范数。 默认情况下，它返回所有样本损失的平均值。

loss = nn.MSELoss()

3.3.6. 定义优化算法

梯度下降

trainer = torch.optim.SGD(net.parameters(), lr=0.03)

3.3.7. 训练

num_epochs = 3
for epoch in range(num_epochs):
    for X, y in data_iter:
        l = loss(net(X) ,y)
        trainer.zero_grad()  # 梯度清零
        l.backward()             
        trainer.step()       # 梯度更新
        
    l = loss(net(features), labels)
    print(f'epoch {epoch + 1}, loss {l:f}')

epoch 1, loss 0.000284
epoch 2, loss 0.000105
epoch 3, loss 0.000105

w = net[0].weight.data
print('w的估计误差：', true_w - w.reshape(true_w.shape))
b = net[0].bias.data
print('b的估计误差：', true_b - b)

w的估计误差： tensor([-4.8637e-04,  9.6798e-05])
b的估计误差： tensor([0.0011])

3.4. softmax回归

3.4.1. 分类问题

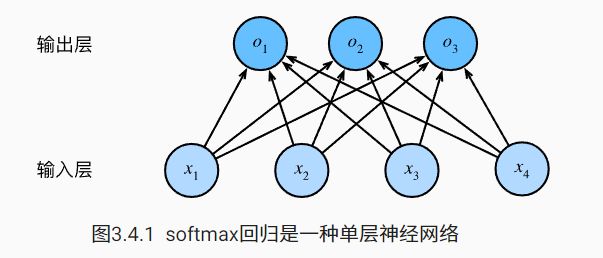
3.4.2. 网络架构

3.4.4. softmax运算

3.4.5. 小批量样本的矢量化

3.4.6. 损失函数

3.4.6.1. 对数似然

3.4.6.2. softmax及其导数

3.4.6.3. 交叉熵损失

3.5. 图像分类数据集

%matplotlib inline
import torch
import torchvision            #对计算机视觉实现的库
from torch.utils import data  #读取数据小批量的函数
from torchvision import transforms  # 对数据进行操作
from d2l import torch as d2l

d2l.use_svg_display()  #用SVG显示图片

3.5.1. 读取数据集

# 通过ToTensor实例将图像数据从PIL类型变换成32位浮点数格式，
# 并除以255使得所有像素的数值均在0到1之间
trans = transforms.ToTensor()  # 图片转成张量
# 下载数据
mnist_train = torchvision.datasets.FashionMNIST(root="./data", train=True, transform=trans, download=True)
mnist_test = torchvision.datasets.FashionMNIST(root="./data", train=False, transform=trans, download=True)

训练集和测试集分别包含60000和10000张图像
测试数据集不会用于训练，只用于评估模型性能。

len(mnist_train), len(mnist_test)

(60000, 10000)

每个输入图像的高度和宽度均为28像素。 数据集由灰度图像组成，其通道数为1。

mnist_train[0][0].shape

torch.Size([1, 28, 28])

Fashion-MNIST中包含的10个类别，分别为t-shirt（T恤）、trouser（裤子）、pullover（套衫）、dress（连衣裙）、coat（外套）、sandal（凉鞋）、shirt（衬衫）、sneaker（运动鞋）、bag（包）和ankle boot（短靴）。 以下函数用于在数字标签索引及其文本名称之间进行转换。

def get_fashion_mnist_labels(labels):  #@save
    """返回Fashion-MNIST数据集的文本标签"""
    text_labels = ['t-shirt', 'trouser', 'pullover', 'dress', 'coat', 'sandal', 'shirt', 'sneaker', 'bag', 'ankle boot']
    return [text_labels[int(i)] for i in labels]

可以创建一个函数来可视化这些样本。

def show_images(imgs, num_rows, num_cols, titles=None, scale=1.5):  #@save
    """绘制图像列表"""
    figsize = (num_cols * scale, num_rows * scale)
    _, axes = d2l.plt.subplots(num_rows, num_cols, figsize=figsize)
    axes = axes.flatten()
    for i, (ax, img) in enumerate(zip(axes, imgs)):
        if torch.is_tensor(img):
            # 图片张量
            ax.imshow(img.numpy())
        else:
            # PIL图片
            ax.imshow(img)
        ax.axes.get_xaxis().set_visible(False)
        ax.axes.get_yaxis().set_visible(False)
        if titles:
            ax.set_title(titles[i])
    return axes

以下是训练数据集中前几个样本的图像及其相应的标签。

X, y = next(iter(data.DataLoader(mnist_train, batch_size=18)))
show_images(X.reshape(18, 28, 28), 2, 9, titles=get_fashion_mnist_labels(y));

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-z5iKk1E2-1640697552266)(https://gitee.com/zdbya/picgo_image/raw/master/SSL_img/202112282118193.svg+xml)]

3.5.2. 读取小批量

batch_size = 256

def get_dataloader_workers():  #@save
    """使用4个进程来读取数据"""
    return 4

train_iter = data.DataLoader(mnist_train, batch_size, shuffle=True, num_workers=get_dataloader_workers())

我们看一下读取训练数据所需的时间。

# timer = d2l.Timer()
# for X, y in train_iter:
#     continue
# f'{timer.stop():.2f} sec'

3.5.3. 整合所有组件

现在我们定义load_data_fashion_mnist函数，用于获取和读取Fashion-MNIST数据集。
这个函数返回训练集和验证集的数据迭代器。
此外，这个函数还接受一个可选参数resize，用来将图像大小调整为另一种形状

def load_data_fashion_mnist(batch_size, resize=None):  #@save
    """下载Fashion-MNIST数据集，然后将其加载到内存中"""
    trans = [transforms.ToTensor()]   # 图片转成张量
    if resize:
        trans.insert(0, transforms.Resize(resize))
    trans = transforms.Compose(trans)
    mnist_train = torchvision.datasets.FashionMNIST(root="../data", train=True, transform=trans, download=True)
    mnist_test = torchvision.datasets.FashionMNIST(root="../data", train=False, transform=trans, download=True)
    
    return (data.DataLoader(mnist_train, batch_size, shuffle=True, num_workers=get_dataloader_workers()),
             data.DataLoader(mnist_test, batch_size, shuffle=False, num_workers=get_dataloader_workers()))

我们通过指定resize参数来测试load_data_fashion_mnist函数的图像大小调整功能

train_iter, test_iter = load_data_fashion_mnist(32, resize=64)
for X, y in train_iter:
    print(X.shape, X.dtype, y.shape, y.dtype)
    break

torch.Size([32, 1, 64, 64]) torch.float32 torch.Size([32]) torch.int64

3.6. softmax回归的从零开始实现

import torch
from IPython import display
from d2l import torch as d2l

batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)

3.6.1. 初始化模型参数

原始数据集中的每个样本都是 28×28 的图像。
在本节中，我们将展平每个图像，把它们看作长度为784的向量。
在后面的章节中，我们将讨论能够利用图像空间结构的特征， 但现在我们暂时只把每个像素位置看作一个特征。

因此，权重将构成一个 784×10 的矩阵， 偏置将构成一个 1×10 的行向量。

num_inputs = 784
num_outputs = 10

W = torch.normal(0, 0.01, size=(num_inputs, num_outputs), requires_grad=True)
b = torch.zeros(num_outputs, requires_grad=True)

3.6.2. 定义softmax操作

def softmax(X):
    X_exp = torch.exp(X)
    partition = X_exp.sum(1, keepdim=True)  # 维度：（m, 1）
    return X_exp / partition  # 这里应用了广播机制

正如你所看到的，对于任何随机输入，我们将每个元素变成一个非负数。 此外，依据概率原理，每行总和为1。

X = torch.normal(0, 1, (2, 5))
X_prob = softmax(X)
X_prob, X_prob.sum(1)

(tensor([[0.1920, 0.1177, 0.4624, 0.0964, 0.1315],
         [0.0458, 0.2193, 0.2899, 0.2468, 0.1982]]),
 tensor([1., 1.]))

3.6.3. 定义模型

定义softmax操作后，我们可以实现softmax回归模型。

def net(X):
    return softmax(torch.matmul(X.reshape((-1, W.shape[0])), W) + b)

3.6.4. 定义损失函数

我们创建一个数据样本y_hat，其中包含2个样本在3个类别的预测概率
以及它们对应的标签y。
我们知道在第一个样本中，第一类是正确的预测； 而在第二个样本中，第三类是正确的预测。
我们选择第一个样本中第一个类的概率和第二个样本中第三个类的概率。

y = torch.tensor([0, 2])
y_hat = torch.tensor([[0.1, 0.3, 0.6], [0.3, 0.2, 0.5]])
y_hat[[0, 1], y]

tensor([0.1000, 0.5000])

现在我们只需一行代码就可以实现交叉熵损失函数。

def cross_entropy(y_hat, y):
    return - torch.log(y_hat[range(len(y_hat)), y])

cross_entropy(y_hat, y)

tensor([2.3026, 0.6931])

3.6.5. 分类精度

def accuracy(y_hat, y):  #@save
    """计算预测正确的数量"""
    if len(y_hat.shape) > 1 and y_hat.shape[1] > 1:
        y_hat = y_hat.argmax(axis=1)
    cmp = y_hat.type(y.dtype) == y
    return float(cmp.type(y.dtype).sum())

我们将继续使用之前定义的变量y_hat和y分别作为预测的概率分布和标签。

accuracy(y_hat, y) / len(y)

0.5

同样，对于任意数据迭代器data_iter可访问的数据集， 我们可以评估在任意模型net的精度。

def evaluate_accuracy(net, data_iter):  #@save
    """计算在指定数据集上模型的精度"""
    if isinstance(net, torch.nn.Module): 
        net.eval()  # 将模型设置为评估模式
    metric = Accumulator(2)  # 正确预测数、预测总数
    with torch.no_grad():
        for X, y in data_iter:
            metric.add(accuracy(net(X), y), y.numel())
    return metric[0] / metric[1]

这里定义一个实用程序类Accumulator，用于对多个变量进行累加。
在上面的evaluate_accuracy函数中， 我们在Accumulator实例中创建了2个变量， 分别用于存储正确预测的数量和预测的总数量。 当我们遍历数据集时，两者都将随着时间的推移而累加。

class Accumulator:  #@save
    """在n个变量上累加"""
    def __init__(self, n):
        self.data = [0.0] * n

    def add(self, *args):
        self.data = [a + float(b) for a, b in zip(self.data, args)]

    def reset(self):
        self.data = [0.0] * len(self.data)

    def __getitem__(self, idx):
        return self.data[idx]

由于我们使用随机权重初始化net模型， 因此该模型的精度应接近于随机猜测。 例如在有10个类别情况下的精度为0.1。

evaluate_accuracy(net, test_iter)

0.1481

3.6.6. 训练

在这里，我们重构训练过程的实现以使其可重复使用。

首先，我们定义一个函数来训练一个迭代周期。
updater是更新模型参数的常用函数，它接受批量大小作为参数

def train_epoch_ch3(net, train_iter, loss, updater):  #@save
    """训练模型一个迭代周期（定义见第3章）"""
    # 将模型设置为训练模式
    if isinstance(net, torch.nn.Module):
        net.train()
    # 训练损失总和、训练准确度总和、样本数
    metric = Accumulator(3)
    for X, y in train_iter:
        # 计算梯度并更新参数
        y_hat = net(X)
        l = loss(y_hat, y)
        if isinstance(updater, torch.optim.Optimizer):
            # 使用PyTorch内置的优化器和损失函数
            updater.zero_grad()
            l.sum().backward()
            updater.step()
        else:
            # 使用定制的优化器和损失函数
            l.sum().backward()
            updater(X.shape[0])
        metric.add(float(l.sum()), accuracy(y_hat, y), y.numel())
    # 返回训练损失和训练精度
    return metric[0] / metric[2], metric[1] / metric[2]

在展示训练函数的实现之前，我们定义一个在动画中绘制数据的实用程序类Animator， 它能够简化本书其余部分的代码。

class Animator:  #@save
    """在动画中绘制数据"""
    def __init__(self, xlabel=None, ylabel=None, legend=None, xlim=None,
                 ylim=None, xscale='linear', yscale='linear',
                 fmts=('-', 'm--', 'g-.', 'r:'), nrows=1, ncols=1,
                 figsize=(3.5, 2.5)):
        # 增量地绘制多条线
        if legend is None:
            legend = []
        d2l.use_svg_display()
        self.fig, self.axes = d2l.plt.subplots(nrows, ncols, figsize=figsize)
        if nrows * ncols == 1:
            self.axes = [self.axes, ]
        # 使用lambda函数捕获参数
        self.config_axes = lambda: d2l.set_axes(
            self.axes[0], xlabel, ylabel, xlim, ylim, xscale, yscale, legend)
        self.X, self.Y, self.fmts = None, None, fmts

    def add(self, x, y):
        # 向图表中添加多个数据点
        if not hasattr(y, "__len__"):
            y = [y]
        n = len(y)
        if not hasattr(x, "__len__"):
            x = [x] * n
        if not self.X:
            self.X = [[] for _ in range(n)]
        if not self.Y:
            self.Y = [[] for _ in range(n)]
        for i, (a, b) in enumerate(zip(x, y)):
            if a is not None and b is not None:
                self.X[i].append(a)
                self.Y[i].append(b)
        self.axes[0].cla()
        for x, y, fmt in zip(self.X, self.Y, self.fmts):
            self.axes[0].plot(x, y, fmt)
        self.config_axes()
        display.display(self.fig)
        display.clear_output(wait=True)

接下来我们实现一个训练函数， 它会在train_iter访问到的训练数据集上训练一个模型net。
该训练函数将会运行多个迭代周期（由num_epochs指定）。
在每个迭代周期结束时，利用test_iter访问到的测试数据集对模型进行评估。
我们将利用Animator类来可视化训练进度。

def train_ch3(net, train_iter, test_iter, loss, num_epochs, updater):  #@save
    """训练模型（定义见第3章）"""
    animator = Animator(xlabel='epoch', xlim=[1, num_epochs], ylim=[0.3, 0.9], legend=['train loss', 'train acc', 'test acc'])
    for epoch in range(num_epochs):
        train_metrics = train_epoch_ch3(net, train_iter, loss, updater)
        test_acc = evaluate_accuracy(net, test_iter)
        animator.add(epoch + 1, train_metrics + (test_acc,))
    train_loss, train_acc = train_metrics
    assert train_loss < 0.5, train_loss
    assert train_acc <= 1 and train_acc > 0.7, train_acc
    assert test_acc <= 1 and test_acc > 0.7, test_acc

小批量随机梯度下降来优化模型的损失函数，设置学习率为0.1

lr = 0.1

def updater(batch_size):
    return d2l.sgd([W, b], lr, batch_size)

现在，我们训练模型10个迭代周期。 请注意，迭代周期（num_epochs）和学习率（lr）都是可调节的超参数。
通过更改它们的值，我们可以提高模型的分类精度。

num_epochs = 10
train_ch3(net, train_iter, test_iter, cross_entropy, num_epochs, updater)

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-SKNJIsSe-1640697552267)(https://gitee.com/zdbya/picgo_image/raw/master/SSL_img/202112282118367.svg+xml)]

3.6.7. 预测

def predict_ch3(net, test_iter, n=6):  #@save
    """预测标签（定义见第3章）"""
    for X, y in test_iter:
        break
    trues = d2l.get_fashion_mnist_labels(y)
    preds = d2l.get_fashion_mnist_labels(net(X).argmax(axis=1))
    titles = [true +'\n' + pred for true, pred in zip(trues, preds)]
    d2l.show_images(X[0:n].reshape((n, 28, 28)), 1, n, titles=titles[0:n])

predict_ch3(net, test_iter)

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-QxYZh3Rk-1640697552268)(https://gitee.com/zdbya/picgo_image/raw/master/SSL_img/202112282118440.svg+xml)]

3.7. softmax回归的简洁实现

import torch
from torch import nn
from d2l import torch as d2l

batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)

3.7.1. 初始化模型参数

我们仍然以均值0和标准差0.01随机初始化权重。

# PyTorch不会隐式地调整输入的形状。因此，
# 我们在线性层前定义了展平层（flatten），来调整网络输入的形状
net = nn.Sequential(nn.Flatten(), nn.Linear(784, 10))

def init_weights(m):
    if type(m) == nn.Linear:
        nn.init.normal_(m.weight, std=0.01)

net.apply(init_weights);

3.7.2. 重新审视Softmax的实现

loss = nn.CrossEntropyLoss()

3.7.3. 优化算法

当我们实例化一个SGD实例时，我们要指定优化的参数 （可通过net.parameters()从我们的模型中获得）以及优化算法所需的超参数字典。
小批量随机梯度下降只需要设置lr值，这里设置为0.03。

trainer = torch.optim.SGD(net.parameters(), lr=0.1)

3.7.4. 训练

num_epochs = 10
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, trainer)

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-2cEMdnj2-1640697552269)(https://gitee.com/zdbya/picgo_image/raw/master/SSL_img/202112282116320.svg)]