目标跟踪(二)：拓展卡尔曼滤波(EKF)

目标跟踪(二)：拓展卡尔曼滤波(EKF)

我们在上一篇文章已经讲述了线性卡尔曼滤波(KF)，也进行了详细的理论推导。但是，由于我们生活中存在很多非线性环节，这就使得线性卡尔曼滤波无法使用，在这一篇文章，我们将针对非线性环节，讨论介绍拓展卡尔曼滤波(EKF)。当然了，理解这篇文章的前提，是看懂上一篇文章。若上篇文章已懂，那么这篇文章就很简单。

---

写在最前面

在这里，不知道有没有一些朋友有以下问题？

为什么变为非线性环节，线性卡尔曼滤波就不能用呢？
当变为非线性环节的时候，叠加定理和齐次定理便不在满足。我们滤波的目的是为了去除噪声，假如我们假设噪声是服从高斯分布的，当通过非线性环节的时候，这个噪声的分布肯定已经不在是高斯分布了，所以我们不能在使用线性卡尔曼滤波进行之前的递推。

因此我们引入了非线性滤波

---

扩展卡尔曼滤波的原理(EKF)

以上便是拓展卡尔曼滤波的核心内容。

---

写在最后

在这里，小编想说，其实拓展卡尔曼滤波就是将非线性环节进行线性化，使用泰勒展开，只用一阶，省略到高阶项。我们这样做的话又引入了线性化误差，因为我们人为的省略掉了高阶项。下一遍文章我们将介绍另一种线性化的方法，即无迹变换以及无迹卡尔曼滤波(UKF)。

---

Matalb仿真分析

仿真参数

在这里，我们仅仅将观测环节设为非线性环节，观测量为目标相对于观测站的角度。

---

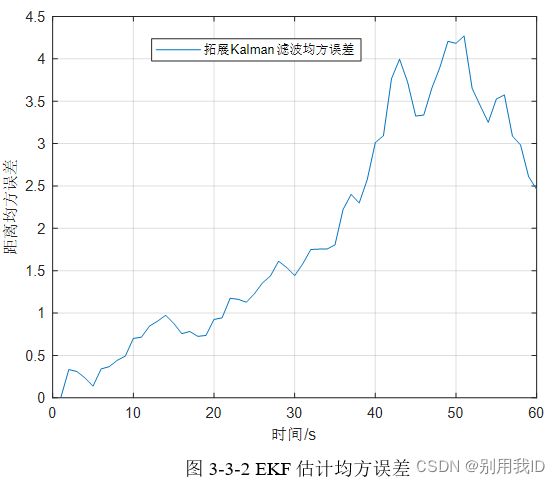
根据仿真结果，我们可以看到，当观测环节由线性环节变为非线性环节，跟踪的误差明显增大。

---

Matalb代码如下

% 拓展卡尔曼滤波在目标跟踪过程中的应用，非线性环节为观测环节，观测的目标的方位
% 观测方程：Z(k) = atan((y(k)-Xstation(2))/(x(k)-Xstation(1))) + v(k)
clear;close all;
T = 1;
N = 60;
F = [1,T,0,0;
     0,1,0,0;
     0,0,1,T;
     0,0,0,1]; %二维CV模型
X0 = [100 2 200 20]';Qk = diag([0.1 0.01 0.1 0.01]);Rk = 0.1;
P0 = diag([0.1 0.01 0.1 0.01]);
Xstation = [0;0];
Xk = Track(X0,Qk,F,N/T);Zk = Measurements(Xk,Rk,Xstation); % 观测方程为非线性表达，所以直接在函数里面进行计算
[Xekf] = EKF(X0,F,Zk,Qk,Rk,P0,Xstation);

figure()
plot(Xk(1,:),Xk(3,:),'LineWidth',1);hold on;
plot(Xekf(1,:),Xekf(3,:),'LineWidth',1);grid on;
legend('真实轨迹','EKF估计航迹')
delta = sqrt((Xk(1,:)-Xekf(1,:)).^2+(Xk(3,:)-Xekf(3,:)).^2);
figure()
plot(delta);grid on
xlabel('时间/s');ylabel('距离均方误差');
legend('拓展Kalman滤波均方误差')

%--------------------------------------------------------------------------
%% 子函数部分
function Xk = Track(X0,Qk,F,N)
% 目标的真实航迹
%%输入参数
% X0 - 状态初值
% Qk - 过程噪声协方差
% Fx - 转移矩阵
% N - 仿真总结拍
%%输出参数
% Xk - 真实航迹

n_x = length(X0); % 状态向量维度
Xk = zeros(n_x,N);Xk(:,1) = X0;
for ii = 2:N
    Xk(:,ii) = F*Xk(:,ii-1) + Qk*randn(n_x,1);

end
end
%--------------------------------------------------------------------------
function Zk = Measurements(Xk,Rk,Xstation)
% 传感器量测
%输入参数
% Xk - 真实航迹
% Rk - 量测噪声协方差
% Xstation - 观测站的坐标
%输出参数
% Zk - 传感器量测值


N = length(Xk(1,:)); % 仿真总节拍
Zk = zeros(1,N);
for ii = 1:N
    Zk(ii) = atan((Xk(3,ii)-Xstation(2))/(Xk(1,ii)-Xstation(1)))+Rk*randn(1);
end
end
%--------------------------------------------------------------------------
function [Xekf] = EKF(X0,F,Zk,Qk,Rk,P0,Xstation)
% 拓展卡尔曼滤波
%输入参数
% X0 - 滤波初值
% F - 转移矩阵
% Zk - 传感器量测
% Qk - 过程噪声协方差
% Rk - 量测噪声协方差
% Xstation - 观测站坐标
%输出参数
% Xekf - 状态估计

n_x = length(X0); % 状态向量维数
N = length(Zk); % 仿真总节拍
Xekf = zeros(n_x,N);Xekf(:,1) = X0;
Pk_Last = P0; % 协方差初始化
for ii = 2:N
    Xekf_hat = F*Xekf(:,ii-1); % 先验估计
    Pk = F*Pk_Last*F' + Qk; % 先验协方差矩阵
    H = [-(Xekf_hat(3)-Xstation(2))/((Xekf_hat(1)-Xstation(1))^2+(Xekf_hat(3)-Xstation(2))^2),0,...
        (Xekf_hat(1)-Xstation(1))/((Xekf_hat(1)-Xstation(1))^2+(Xekf_hat(3)-Xstation(2))^2),0];%即为所求一阶近似
    Kk = Pk*H'/(H*Pk*H'+Rk); % 卡尔曼增益
    Zzk = atan((Xekf_hat(3)-Xstation(2))/(Xekf_hat(1)-Xstation(1)));
    Xekf(:,ii) = Xekf_hat + Kk*(Zk(ii)-Zzk); % 后验估计
    Pk_Last = (eye(n_x)-Kk*H)*Pk; % 更新误差协方差
end
end