西瓜书笔记--第二章 模型评估与选择

2.1 经验误差 过拟合 欠拟合

首先依旧给出一些定义：
1、错误率（error rate）：分类错误的样本数占样本总数的比例
2、精度（accuracy）：1-错误率
3、训练误差/经验误差（empirical error）：学习器在训练集上的误差
4、泛化误差：学习器在新样本上的误差
我们希望的是在新样本上表现的很好的学习器，所以目标为使泛化误差尽可能的小，但是我们靠训练集上的数据只能做到减小经验误差，以求能达到学到样本的“普遍规律”，这样在面对新样本时也可以有正确的判别。

但是这并不意味着要把训练样本完全的学的“特别好”，这样很可能将训练样本自身的一些特点当作所有潜在样本都具有的一些一般性质，导致泛化性能下降，这种现象就称为“过拟合”，同样的如果对训练样本的一些一般性质尚未学好，这样就有可能产生“欠拟合”，打个比方，过拟合就是对于问题太过于死记硬背，而欠拟合则是面对问题没有足够努力。

欠拟合的解决方法比较多：例如在决策树学习中扩展分支，在神经网络学习中增加训练轮数等等（本质上就是继续学习训练样本）而过拟合则比较难解决，完全解决过拟合的问题相当于解决P=NP的问题，所以过拟合一般无法避免，但是有手段去改善（增加正则项、early stop等等）

2.2 评估方法

前面已经说过，机器学习的最终目标是使泛化误差尽可能的小，但是在学习过程中只有经验误差的产生，所以我们需要一个测试集来测试学习器在新样本上的判别能力。下面我们考虑如何选择，可以让测试集上的测试误差作为泛化误差的近似。

测试集应该尽可能的与训练集互斥，即测试样本尽量不在训练集中出现。这个很好理解，如果测试集中的样本即为训练集中的样本，那么测试集上的测试误差就与训练误差正相关，这样即便出现了过拟合现象，但是测试误差却很小，那么我们就无法判断是是否过拟合了。

所以训练集的选择方法即为：对于包含所有数据的数据集D进行适当的处理，从中选出训练集S和测试集T。下介绍几种常用的方法：

2.2.1 留出法（hold-out）：将数据集D划分为两个互斥的集合，一个集合作为训练集S，另一个作为测试集T。

值得注意的是：在划分训练集和测试集的时候，要尽可能保持数据分布的一致性，即保持样本类别比例相似。这种采样通常被称为“分层采样”；另一方面，即使我们给定了类别比例，任然存在多种对初始数据集D进行分割的方式（这是显然的，相当于排列组合问题）所以我们一般要采用若干次随机划分、重复进行实验评估后取平均值作为留出法的评估结果。

分层采样的窘境：若令训练集S包含绝大多数样本，则模型会接近于直接用D训练出的模型，但此时T比较小，评估结果可能不准确；然而若令T包含多一些样本，则S与D差别更大了，模型可能与直接用D训练出的模型有差别。这个问题没有完美的解决方案

常见做法：将大约2/3~4/5的样本用于训练，剩余样本用于测试

2.2.2 交叉验证法：将数据集D划分为k个大小相似的互斥子集，每个子集Di都尽可能保持数据分布的一致性（即均从D中分层采样获得）每次用k-1个子集的并集作为训练集，余下那个子集作为测试集，从而进行k次训练和测试，最终返回k个测试结果的均值。通常把交叉验证法称为“k折交叉验证（k-fold cross validation）”k一般取10。（如图2.2所示）

与留出法相似的，将数据集D划分为k个子集同样存在多种划分方式，所以也要随机使用不同的划分重复p次，最终评估结果是p次k折交叉验证结果的均值

特别的，如果令k=m（D中样本个数），则得到了交叉验证法的一个特例：留一法（Leave-One-Out），即训练集与初始数据集相比只少了一个样本。留一法中被评估的模型与直接用D训练出来的模型很相似。然而在数据集比较大时，训练m个模型的计算开销可能是难以忍受的。

2.2.3 自助法：给定包含m个样本的数据集D，我们对它进行采样产生数据集Ｄ’，每次随机从D中挑选一个样本，将其拷贝放入D’中，然后再将该样本放回D中，直到有包含m个数据的训练集D’

可以估计，一个样本在m次取样中都不被选中的概率为：(1-1/m)^m，当m趋向于无穷时，概率趋向于1/e,所以约为1/3的样本不会出现在训练集中，于是我们将剩余没有被选中的样本作为测试集。

自助法在数据集较小，难以有效划分训练集和测试集时很有用，此外，自助法可以从初始数据集中产生多个不同训练集，这对集成学习等方法有很大好处。然而，自助法产生的数据集改变了初始数据集的分布，这会引入估计偏差（一个样本被选中多次，那么这个样本在数据集D’中对最后模型的重要性就大于在D中的重要性）

总的来说，在初始数据量足够时，留出法和交叉验证法更常用一些；而如果数据集较小，则使用自助法。

调参与最终模型
大多数学习算法都有参数需要设定，所以选择模型既要对学习算法进行选择，也要在选定算法后对参数进行设定。
参数的选择往往是一个困难的问题，我们可以通过一定的步长对较优参数进行搜索求解。此外，我们一般会将训练数据划分为训练集和验证集：1、先使用训练集进行学习，2、不同算法、不同参数在验证集上的效果进行比较，从而进行模型选择和调参，3、最后用最终模型在测试集的判别效果来估计模型在实际使用时的泛化能力。（三个集合都应该是互斥的）

性能度量

性能度量，就是衡量模型泛化能力的评价标准。（以下针对监督学习）
在预测任务中，给定样例集D，评估学习器f的性能，就是把学习器预测结果f(x)与真实标记y进行比较。
以下列举一些常用的性能度量（摘自西瓜书）

下面我们着重考虑分类任务中常用的性能度量：
2.3.1 错误率与精度
错误率与精度的定义我们前面已经给出（本章最开头）对于样例D有：

2.3.2 查准率 查全率 F1
除了考虑错误率和精度，我们在实际应用中还会有其他任务需求。例如在西瓜问题中，我们可能关心的是“挑出的瓜中有多少比例确实是好瓜”、“所有好瓜中有多少比例被挑出来了”，这就分别对应了查准率和查全率。

在补充查准率和查全率的概念之前，我们先引入混淆矩阵(confusion matrix)

TP表示真正例(true positive)，FN(false negative)表示假反例，FP(false positive)表示假正例，TN(true negative)表示真反例。他们的含义由混淆矩阵已经给出。
查准率P的定义为：P=TP/(TP+FP)=真正例个数/被预测为正例个数
查全率R的定义为：R=TP/(TP+FN)=真正例个数/正例实际个数
（再次重复这里的真正例TP含义为：被预测为正例的正例）

查准率和查全率往往不能同时都很高，所以我们往往会根据问题的需要选择。我们根据学习器的预测结果对样例进行排序，排在前面的是学习器认为“最可能”是正例的样本，排在后面的则是学习器认为“最不可能”是正例的样本。以此顺序逐个把样本作为正例进行预测，则每次可以计算出当前的查全率、查准率。以查准率为纵轴，查全率为横轴作图，就得到了“P-R曲线”
（即选取不同的阙值，大于阙值的判定为正例，否则为负例，不同阙值对应不同的查全率和查准率）如图2.3所示：

举个简单的例子：
例子1：假设我们的分类器对于10个数据的预测结果如下：

预测值（大小排名）	真实值
1	+
2	+
3	-
4	+
5	-
6	-
7	+
8	+
9	-
10	-

我们不妨定义0/0=1,
于是如果我们将阙值放在预测值排名第一的上方，即所有数据都会被判为负例，则此时有：TP=0 FP=0 TN=5 FN=5
P=TP/TP+FP=0/0=1 R=TP/TP+FN=0/5=0 （R，P）=（0，1）
阙值放在1-2之间：TP=1 FP=0 TN=5 FN=4
P=1/1=1 R=1/5(R,P)=(1/5,1)
以此类推
一直到阙值放在10号的下面，即所有数据被判为正例
此时：TP=5 FP=5 FN=0 TN=0
P=5/10=1/2 R=5/5=1 (R,P)=(1,1/2)
我们可以得到11个点，它们的连线就是P-R曲线。

图2.3还给我们带来了一个问题：图中算法A、B在所有点上都是优于算法C的，但是A、B之间的比较却不能一般性的断言孰优孰劣。我们所希望的算法是查准率、查全率都高的，所以引入一些新的性能度量：
平衡点/BEP（Break-Event Point），是算法在查准率=查全率时候的取值（即y=x与P-R曲线的交点的横/纵坐标）
F1度量 ：F1=2×P×R/P+R
可以推导出1/F1=(1/P+1/R)(1/2),由调和平均的性质：P、R中的较小值更能影响F1的值。
Fβ度量：Fβ=(（1+β^2)×P×R)/((P×β ^2)+R)

β的不同取值度量了查全率和查准率的相对重要性：β=1时即为F１度量，β＞1时　查全率有更大影响；β＜1时，查准率有更大影响。

此外，当我们进行多次训练/测试时，得到多个训练矩阵，则此时对查准率和查全率的计算有两种方式（先计算后平均/先平均后计算）

2.3.3 ROC与AUC
前面已经提到过，很多学习器是对测试样本产生一个实值或概率预测，将预测值与分类阙值进行比较，若大于阙值则为正类，否则为负类。在一些特定的问题中，我们更重视“查准率”，则选择排序中靠前的位置进行截断；重视“查全率”，则选择排序中靠后的位置进行截断。

下面继续介绍一些性能度量：
ROC曲线：根据学习器的预测结果对样例进行排序，按不同的阙值对样本进行预测，从而得到两个参数的值（与获得P-R曲线的方法一样）：真正例率和假正例率
真正例率：TPR=TP/TP+FN=真正例数/正例实际个数
假正例率：FPR=FP/TN+FP=假正例数/负例实际个数
分别以真正例率和假正例率为横纵坐标作图，就得到了“ROC曲线”。
如图2.4所示：

如果两个学习器的ROC曲线发生交叉，那么难以一般性的断言两者孰优孰劣，这时合理的判据是比较AUC曲线下的面积，即AUC（Area Under ROC Curve)
AUC有估算公式：

或者：


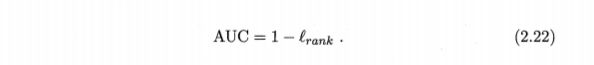
前面一个的证明是显然的，下列出对2.22式的证明（摘自第二次作业…截屏word文档里的）


容易证明上面的结论与式2.21+2.22是等价的。

2.3.4 代价敏感错误率与代价曲线
我们引入的性能度量都是与实际应用中有关联，下面也不例外。由于不同类型的错误所造成的后果往往不同，比如把患者诊断为健康人和把健康人诊断为患者，前者可能危及生命，后者则是可能需要进一步检查的麻烦。为权衡不同类型错误所造成的不同损失，可为错误赋予“非均等代价（unequal cost)”
以二分类任务为例，我们可以根据任务领域知识设定一个“代价矩阵（cost matrix)”如表2.2所示：

由我们设定的代价矩阵我们可以定义代价敏感错误率

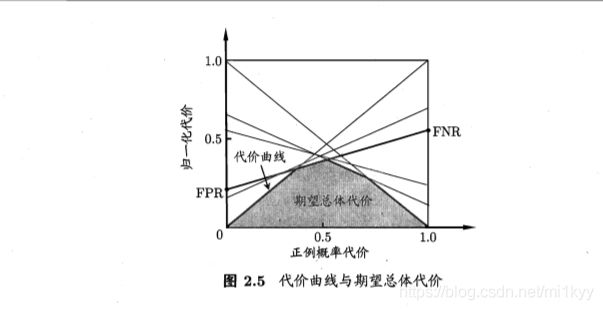
在非均等代价下，我们采用“代价曲线”代替ROC曲线，来反应学习器的期望总体代价（总错误率）。代价曲线的横轴、纵轴分别为正例概率代价和归一代价，定义如下：

其中FNR=FN/TP+FN, FPR=FP/TN+FP
不同阙值下我们可以得到不同的（FNR,FPR)值对，容易推导出：
cost_norm=FNR* P(+)+FPR* (1-P(+))

所以根据不同的（FNR,FPR)值对，我们可以在代价平面上获得不同的线段，我们定义线段下的面积即表示了该条件下的期望总体代价。取所有线段的下界，所得的面积就是在所有条件下的期望总体代价。
（这个定义是我自己杜撰的，书上并没有说为什么这样就是期望总体代价，个人理解就是这么定义的…）
代价曲线我的理解并不是很到位，知乎上有一个问题就是关于这个的理解，高赞答案感觉挺到位的，附链接：
https://www.zhihu.com/question/63492375
如图2.5所示

2.4 比较检验

这一部分比较多的是概率统计里的内容，仅仅把可用的方法罗列，具体使用可以调用一些R/matlab 里的库函数
单个学习器泛化性能的假设检验：常用的方法有二项检验和t检验。
不同学习器的性能比较：常用方法：交叉验证t检验（5×2交叉验证法）、McNemar检验、Friedman检验与Nemenyi后续检验。具体内容等到后面想到了再补充…

2.5 偏差与方差

偏差-方差分解：




推导摘自于南瓜书，3-4步的推导略微麻烦了些，考虑到yD和f(x,D)相互独立，f_(x)为常数，则（f(x,D)-f_(x))和(f_(x)-yD)也相互独立，直接使用E(AB)=E(A)*E(B)，其中E（f(x,D)-f_(x))= 0 便可以直接得出。
（推导的关键在于认识到 f(x,D),yD为相互独立的随机变量，其余均为常量）