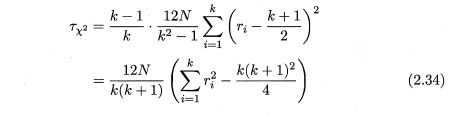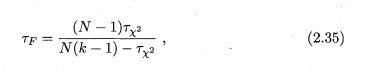西瓜书第二章笔记及答案——模型评估与选择

第2章 模型评估与选择

2.1经验误差与过拟合

错误率error rate：分类错误的样本占总样本的比例
精度accuracy：1-错误率
误差error：实际预测输出与真是输出之间的差异，在训练集上的误差成为训练误差training error或经验误差empirical error，在新样本上的误差成为泛化误差generalization error
训练的最终目标是获得较小的泛化误差，但是实际能做的是努力使训练误差较小，然而经验误差小的模型，其泛化误差不一定小。
为了获得较小的泛化误差，需要从训练集上尽可能学出适用于整个样本空间的“普遍规律”，当学习器把训练样本学得太好时，可能将训练集本身存在的规律当作整个样本空间的“普遍规律”，导致泛化能力下降。
过拟合overfitting、过配：训练误差很小，而泛化误差很大
欠拟合underfitting、欠配：训练误差很大
学习能力过于强大是导致过拟合最常见的原因，而欠拟合通常是由于学习能力低下
学习能力由学习算法和数据内涵决定
欠拟合容易客服，过拟合比较麻烦，过拟合是无法彻底避免的，各类算法必须带有缓解过拟合的措施
模型选择model selection：对学习算法、参数配置的选择

2.2评估方法

现实任务需要考虑时间开销、存储开销、可解释性、泛化误差等因素。
测试集testing set：测试学习器对新样本的泛化能力，将在测试集上的测试误差testing error作为泛化误差的近似，测试集应该当尽量与训练集互斥

2.2.1留出法

留出法hold-out：直接将数据集D划分为两个互斥的集合，其中一个作为训练集S，另一个作为测试集T
训练/测试集的划分尽可能保持数据的一致性，采用分层采样stratified sampling
单次使用留出法得到的评估结果往往不够稳定可靠，在使用留出法时，一般采用若干次随机划分、重复进行实验评估后取平均值作为留出法的评估结果
当训练集S很大而测试集T很小时，评估结果不够准确，方差大；当测试集T包含很多样本时，训练得到的模型与用D得到的模型有很大差别，偏差大。

2.2.2交叉验证法

交叉验证法cross validation、k折交叉验证k-fold cross validation：先将数据集D划分为k个大小相似的互斥子集，每个子集尽可能保持数据分布的一致性。然后每k-1个子集作为训练集，余下的子集作为测试集；这样就可以获得k组训练/测试集，进行k次训练/测试，最终返回k个测试结果的均值。
交叉验证法评估结果的稳定性和保真性很大程度上取决于k的取值
与留出法类似，数据集使用不同方式划分为k个子集，重复多次，取均值，可减小因样本划分不同而引入的差别，通常“10次10折交叉验证”
留一法Leave-One-Out：k折交叉验证种令k=样本个数，因为只存在一种划分方式，所以不受划分方式的影响，并且训练集与D至少一个样本，因此往往认为留一法的评估结果比较准确。缺点：开销大、评估结果未必比其他方法准确

2.2.3自助法

自助法bootstrapping：以自助采样bootstrap sample为基础，从D种重复m次随机采样，获得和D相同大小的训练集D1，D\D1作为测试集。这样的测试结果成为包外估计out-of-bag estimate
自助法适用于数据集较小、难以有效划分训练集/数据集的情况下使用；自助法可以产生多个不同的训练集，对于集成学习有很大好处；自助法产生的数据集改变了初始数据集的分布，这会引入估计偏差，因此当数据量足够时，留出法和交叉验证法更常用

2.2.4调参与最终模型

调参parameter tuning、参数调节：在进行模型评估和选择时，除了要对使用学习的算法进行选择，还要对算法参数进行设定。
机器学习涉及两类参数：算法的参数——超参，模型的参数。两者的调参方式类似，都是产生模型之后根据某种评估方法进行选择，不同之处在于前者是人工设定，后者是通过学习获得。
由于参数的取值往往是实数域，现实任务中不可能把所有的参数配置出模型，需要设定范围和步长，在计算开销和性能估计之间做出选择。
验证集validation set：用于模型评估和选择

2.3性能度量

性能度量performance measure：衡量模型泛化能力的评价指标
性能度量反映了模型的“好坏”，对于不同的任务需求，应当使用对应不同的合适的性能度量

2.3.1错误率和精度

错误率和精度是分类任务中常用的两种性能度量
错误率是分类错误的样本数占总样本数的比例，精度是分类正确的样本占总样本数的比例

2.3.2查准率、查全率与F1

查准率precision、准确率：$\frac{真正例}{预测所有正例}$

查全率recall、召回率：$\frac{真正例}{样本所有正例}$
混淆矩阵confusion matrix：预测情况和真实情况组成的矩阵
查准率和查全率是一对毛对的度量，一般查准率偏高时查全率偏低，查准率偏低时查全率偏高。通常只有在一些简单的任务中才能使查全率和查准率都很高。
PR曲线：反映训练过程中查准率和查全率变化的曲线
若一个学习器的PR曲线被另个一学习器的PR曲线完全包住，可以认为后者的性能优于前者，人们通常综合考虑查准率和查全率
平衡点Break-Even Point：PR曲线上查准率=查全率的点
F1度量：查准率和查全率的调和平均harmonic mean，与算术平均、几何平均相比，调和平均更重视较小值
$F_{\beta }$：查准率和查全率的加权调和平均，可以通过调整$\beta$来调整查全率和查准率的重视程度
宏查准率macro-P：所有混淆矩阵的查准率的均值
宏查全率macro-R：所有混淆矩阵的查全率的均值
宏F1：宏查准率和宏查全率的调和平均
也可以先将所有的混淆矩阵进行平均，得到一个新的混淆矩阵，进而计算出微查准率、微查全率、微F1

2.3.3ROC与AUC

受试者工作特征Receiver Operating Characteristic(ROC):横坐标是假正例率、纵坐标是真正利率
AUC（Area Under ROC Curve）：ROC曲线下方的面积

形式化来看AUC考虑的是排序的质量和排序误差紧密联系。
排序损失loss：

2.3.4代价敏感错误率与代价曲线

非均等代价unequal cost：不同错误造成的不同程度的损失
代价矩阵cost matrix：表示不同预测结果的代价的矩阵
在非均等代价下，我们希望最小化总体代价total cost
代价敏感cost-sensitive错误率

在非均等代价下，ROC曲线不能直接反映出学习器的期望总体代价，而代价曲线cost curve可以
代价曲线的横轴是正例概率代价，纵轴是归一化代价


规范化normalization：将不同变化范围的值映射到相同的固定范围，常见的是[0,1]，又称归一化

2.4比较检验

实验评估方法是对学习器进行训练和评估的方法，性能度量是对学习器性能的度量，比较检验是如何对性能度量进行比较。
机器学习性能度量比较复杂的原因：
1.通过实验评估方法获得的是测试集上的性能，与泛化性能未必相同
2.测试集上的性能与测试集的选择有很大关系
3.很多机器学习算法本身具有随机性，相同的参数配置在同一测试集上多次运行的结果可能不同
比较学习器性能的重要依据：假设检验hypothesis test

二项检验binomial test、t检验t-test:对单个学习器泛化性能的假设进行检验
交叉验证t检验、McNemar检验：在一个数据集上比较两个算法
在k-折交叉验证中，不同轮次的训练集会有一定重叠，因此测试性能实际上并不是独立的，为了缓解这一问题，可以采用5*2交叉验证。
在多个数据集上比较多个算法：Friedman检验、Nemenyi后续检验
首先使用Friedman检验，当“所有算法的性能相同”假设被拒绝后，再使用Nemenyi后续检验，检验哪些算法性能相同，哪些不同。

2.5偏差与方差

偏差-方差分解：解释学习算法泛化性能的重要工具
基于均方误差的回归问题，算法的期望泛化误差可以分解为偏差、方差、噪声的和。
偏差刻画了预测结果与真是结果的偏离程度，表示学习算法的拟合能力；方差度量了训练集的变动对学习性能的影响；噪声则是当前任务上所有学习算法所能达到的期望泛化误差的下限。
一般来说，偏差和方差是冲突的，随着训练程度提高，偏差下降、方差上升。

习题

2.1

为了保持数据分布的一致性，采用分层抽样，500个正例中350个是训练集，150个是测试集；500个反例也是如此划分
$C_{500}^{350}\ast C_{500}^{350}$

2.2

(1)10折交叉验证：为了保持数据分布的一致性，采用分层抽样，10个子集中各有5个正例、5个反例，所以训练集中正反例的数目相同，所以学习器会随即猜测，错误率为50%。
(2)留一法：如果测试集为一个反例，则训练集中正例必然多于反例；若测试集为一个正例，则训练集中反例必然多于正例。所以，错误率为100%。

2.3

根据定义，


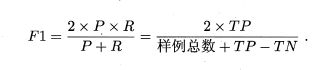
可知，对于多次实验获取的一条PR曲线，只有一个平衡点，而F1可以根据PR曲线上每一点的P和R进行计算。
假设对于PR曲线的所有点计算的F1值，A学习器都高于B学习器，则在平衡点处的F1值，A也高于B。
此时，有
$$F1=\frac{2\ast P\ast R}{P+R}=\frac{2\ast P\ast P}{P+P}=P$$
所以,在平衡点处，F1和BEP相等，因此A的BEP也高于B

2.4

查全率=真正例率

2.5

AUC是ROC曲线下方的面积，可以分割成一系列小长方形的面积之和

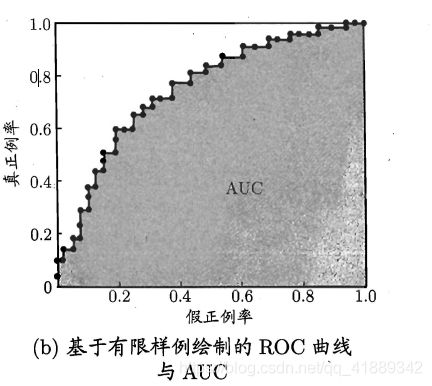
根据绘制AUC的过程，不难看出上述面积可以分割成$m_{-}$个小长方形（遇到假正例时才会在横轴方向产生$\frac{1}{m_{-}}$的宽度，遇到真正例时才会在纵轴方向产生$\frac{1}{m_{+}}$的高度），每个长方形的宽度为$\frac{1}{m_{-}}$，高度为$\frac{该假正例前真正例个数}{m_{+}}$,所以有(不考虑正反例预测值相同,预测值越大排位越靠前)
$$\begin{gathered} AUC=\frac{1}{m_{-}}\sum _{i=1}^{m_{-}}\sum _{x^{+}\in D^{+}}⨿(f(x^{+})>f(x_i))\ast \frac{1}{m_{+}} \\ =\frac{1}{m_{+}{m}_{-}}\sum _{x^{-}\in D^{-}}\sum _{x^{+}\in D^{+}}⨿(f(x^{+})>f(x^{-})) \end{gathered}$$
根据
$$\sum _{x^{-}\in D^{-}}\sum _{x^{+}\in D^{+}}⨿(f(x^{+})>f(x^{-}))=m_{-}{m}_{+}-\sum _{x^{-}\in D^{-}}\sum _{x^{+}\in D^{+}}⨿(f(x^{+})<f(x^{-}))$$
得
$$\begin{gathered} AUC=\frac{1}{m_{+}{m}_{-}}(m_{-}{m}_{+}-\sum _{x^{-}\in D^{-}}\sum _{x^{+}\in D^{+}}⨿(f(x^{+})<f(x^{-}))) \\ =1-\frac{1}{m_{-}{m}_{+}}\sum _{x^{-}\in D^{-}}\sum _{x^{+}\in D^{+}}⨿(f(x^{+})<f(x^{-})) \\ =1-{\ell }_{rank} \end{gathered}$$

2.6

计算错误率需要事先定义一个分类阈值，当预测值大于阈值时判断为正例，反之为反例；而ROC曲线不需要设定一个固定的阈值，而是遍历所有的截断情况，依次计算真正例率和假正例率，可以利用ROC曲线从整体上比较模型的好坏。

2.7

根据定义，ROC曲线的点坐标为（FPR,TPR），代价曲线的横坐标为

纵坐标为

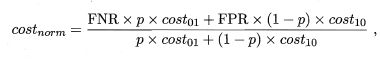
其中$p$为依次截断所产生的正例概率，$FNR=1-TPR$ ，所以可以通过连续ROC曲线的每一点来计算与之对应的代价曲线的每一点坐标，即每一条ROC曲线都可以获得一条与之对应的代价曲线。

反之，在代价曲线上的某一点做切线，便可以获得相应的FPR、FNR，从而计算出ROC。

2.8

Min-max规范化是将原来数据线性变换到规定的最大最小值区间，优点：保留数据原有的关系，简单 ；缺点：若数据极差比较大，则变换后会有很多数据取值非常接近
z-score规范化：Z-Score的主要目的就是将不同量级的数据统一转化为同一个量级，统一用计算出的Z-Score值衡量。优点：保证数据的可比性；缺点：削弱数据的解释性。

2.9

https://wiki.mbalib.com/wiki/%E5%8D%A1%E6%96%B9%E6%A3%80%E9%AA%8C

2.10

使用(2.34)要求k比较大（k>30），所k较小则倾向于认为算法无显著区别；为了缓解这一问题，使用(2.35)