Cross-Domain Few-Shot Classification VIA Learned Feature-Wise Transformation 论文解读
Cross-Domain Few-Shot Classification VIA Learned Feature-Wise Transformation
- 摘要简介:
- 方法:
- FEATURE-WISE TRANSFORMATION LAYER:
- LEARNING THE FEATURE-WISE TRANSFORMATION LAYERS :
- 实验:
摘要简介:
小样本分类的目的是在每一个类别仅有少量标注样本的情况下识别新的类别。当前metric-based(基于度量)的小样本分类方法是:先利用metric function(度量函数)从少量标记数据(support examples)中学习得到feature embeddings,在通过比较query images的feature embeddings来预测新的类。但是现有的方法会在不可见域失败,因为特征在不同域之间的分布差异巨大。在本文中,我们提出了一种metric-based方法解决小样本分类的域漂移(domain shifts)问题。我们的核心思想是在训练阶段,利用feature-wise transformation layers (特征转换层),通过仿射变换增强图像特征,来模拟不同域下的特征分布。为了捕捉各种不同域下的特征分布,我们应用了元学习方法取搜索feature-wise transformation layers的超参。
方法:
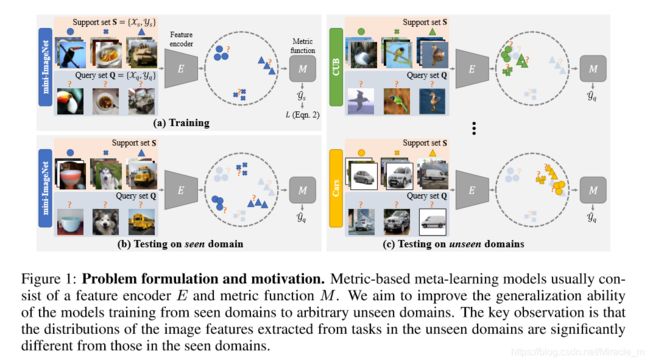
图1是算法的整流思路流程。首先在mini-ImageNet(可见域)上训练,训练出一个encoder。然后在Cars和CUB上(不可见域)进行训练。(为了优化encoder超参)
文章指出主要贡献有三点:
1:提出了利用特征转换层取模拟不同域下的特征分布。本文的特征转换层可以应用到各种metric-based的方法中取提高不可见域的预测
2:提出了一种元学习的方法优化特征转换层的超参。
3:在三个metric-based的方法上(MatchingNet,RelationNet,Graph Neural Networks)进行验证,表明提出的特征转换层可以有效提高在不可见域的能力,并且也验证了元学习优化超参的方法可以提高转换层的表现。
图2是该论文的特征转换层的算法图,也是训练阶段的框图。
Metric-based算法主要包含编码器 E E E和度量函数 M M M。在训练阶段的每一次迭代中,算法都随机的采样 N w N_{w} Nw类,从而构造成一个任务 T T T。
将采样的输入图片表示为 X = { x 1 , x 2 , ⋯ , x n } \mathcal{X}=\left\{\mathbf{x}_{1}, \mathbf{x}_{2}, \cdots, \mathbf{x}_{n}\right\} X={x1,x2,⋯,xn},相关类表示为 Y = { y 1 , y 2 , ⋯ , y n } \mathcal{Y}=\left\{y_{1}, y_{2}, \cdots, y_{n}\right\} Y={y1,y2,⋯,yn}。那么任务 T T T就由support set S = { ( X x , Y s ) } \mathbf{S}=\left\{\left(\mathcal{X}_{x}, \mathcal{Y}_{s}\right)\right\} S={(Xx,Ys)} 和 query set Q = { ( X q , Y q ) } \mathbf{Q}=\left\{\left(\mathcal{X}_{q}, \mathcal{Y}_{q}\right)\right\} Q={(Xq,Yq)}构成。其中 S S S和 Q Q Q分别从 N w N_{w} Nw中抽取 N s N_{s} Ns和 N q N_{q} Nq个类别。
接着,重点是
FEATURE-WISE TRANSFORMATION LAYER:
文章的目的是为了提高metric-based方法在不可见域的泛化能力。造成的原因就是不同域之间数据特征的分布差异。为了解决这个问题,作者首先提出了 feature-wise transformation ,通过在训练阶段放射变换输入数据,模拟不同域之间的特征分布。而编码器 E E E通过 feature-wise transformation 之后能够产生更多样的特征分布,这样就可以提高度量函数 M M M的泛化能力。在图2(b)中可以看到,在BN层后面插入了feature-wise transformation layer。超参 θ γ ∈ R C × 1 × 1 \theta_{\gamma} \in R^{C \times 1 \times 1} θγ∈RC×1×1 和 θ β ∈ R C × 1 × 1 \theta_{\beta} \in R^{C \times 1 \times 1} θβ∈RC×1×1符合高斯分布标准差。
在则一层转换层,给定一个维度为 C × H × W C×H×W C×H×W中间特征激活图 z z z,首先从高斯分布中采样 scaling term γ γ γ 和 bias term β β β ,
γ ∼ N ( 1 , softplus ( θ γ ) ) β ∼ N ( 0 , softplus ( θ β ) ) \gamma \sim N\left(\mathbf{1}, \operatorname{softplus}\left(\theta_{\gamma}\right)\right) \quad \beta \sim N\left(\mathbf{0}, \text { softplus }\left(\theta_{\beta}\right)\right) γ∼N(1,softplus(θγ))β∼N(0, softplus (θβ))
然后计算调制后的激活 z ^ \hat{\mathbf{z}} z^
z ^ c , h , w = γ e × z c , h , w + β c \hat{z}_{c, h, w}=\gamma_{e} \times z_{c, h, w}+\beta_{c} z^c,h,w=γe×zc,h,w+βc
LEARNING THE FEATURE-WISE TRANSFORMATION LAYERS :
为了解决手动调参在困难,该文又提出了 learning-to-learn algorithm 去优化特征转换层的超参。核心思想是在可见域上训练集成转换层的模型来提高在不可见域的能力。
文中的过程描述比较复杂,我直接贴在下面,然后我按照自己的理解进行解读。
每一次训练迭代的时候都采样从可见域 { T 1 seen , T 2 seen , ⋯ , T N seen } \left\{\mathcal{T}_{1}^{\text {seen }}, \mathcal{T}_{2}^{\text {seen }}, \cdots, \mathcal{T}_{N}^{\text {seen }}\right\} {T1seen ,T2seen ,⋯,TNseen }(在文中即为训练用的miniImageNet)中抽取一个可见域 T p s T^{\mathrm{ps}} Tps 和一个伪不可见域 T p u T^{\mathrm{pu}} Tpu(因为其实是可见的,但是为了模拟不可见域从而达到训练效果)。然后按照参数更新的规则进行训练。然后衡量更新后的模型的泛化能力,步骤是
1)去掉特征转换层
2)计算更新后的模型在伪不可见域得loss
这里我在网上看到很多伙伴说去掉了以后那参数怎么更新?怎么求梯度?
那么这里按照我的理解是:这是一个train(训练)和val(验证)的过程,上述衡量泛化能力的步骤其实就是在val,所以是不需要计算梯度,也不需要更新。只需要单纯的计算loss来验证模型更新后的有效性。
再有,为什么要去掉特征转换层?我们回到特征转换层的本质—— augmenting the image features.所以,特征转换层本质上是一个数据增强操作,和我们普通的图像裁剪,旋转等等是一样的。所以我们在验证包括测试的时候,是不需要再增强数据的,特征转换层只是为了模拟不可见域的特征分布,提升模型的泛化性。所以,我们在val和test的的时候,是不需要它的。
实验:
文章再往后都是实验的细节和对比。需要注意的是,文中说特征转换层是加载在每一个残差块的最后一个BN层后面的。
实验结果如下:

整篇文章的脉络和实验的对比还是很清晰的,至于代码的的细节我还没有细看。有机会再进行分享。
有问题的小伙伴可以在评论区留言