机器学习---一 基本概念及入门和线性回归
零 讲讲人工智能
人工智能,emmmmm,机器替代人,是一种大趋势,可能目前局限在计算机、数学等领域,学习了解的人限制于教授、大学生等高知识人才,但学的人完全可以感受到,其门槛在降低,全民AI是一种必然趋势
AI的官方定义是:AI is field that studies the synthesis and analysis of computational agents that act intelligently
大概就是机器能够智能的做出行为
AI主要的方向有两种
一种是思考和行为像人
另一种是可以理性的思考和行为
目前,一般我们期望的是后者,来提高生产力
目前火热的机器学习属于AI,而更火热的深度学习属于机器学习
(个人感觉可以分为广义的机器学习和传统的机器学习,分隔界限就是深度学习的火热)
AI适用的范围,几乎所有领域
一 基本概念
1.1监督学习与无监督学习
最主要的区别是有没有标签
1.1.1监督学习:D=(X,y) 学习X->y的关系
我们想 模型学习什么样的关系呢,如果想学习线性关系就采用线性模型;非线性关系就采用非线性模型;
D表示样本数据 X表示特征 y表示标签
常见算法:
1.线性归回
2.逻辑回归(建立在线性回归之上,解决分类问题)
3.朴素贝叶斯(文本分类)
4.决策树(条件)
5.随机森林(和决策树相关,把所有专家的答案综合考虑一下)
6.SVM(最难的算法)
7.神经网络(最根本的基础)
1.1.2无监督学习:D(X)寻找X中的特征或规律 代表:聚类算法
学不到映射关系
常用无监督学习算法:
1.PCA(降维算法,将高纬的数据映射到低维的空间,降噪、去无用信息,将数据可视化)
2.K-means(聚类算法)
3.GMM (类似于k-means ,k-means是GMM的特例)
4.LDA (抽取主题特征的模型)
1.2 回归与分类问题
主要区别是预测值的形式
1.2.1回归问题:输出的连续性值,比如温度、身高和气温
1.2.2分类问题:输出的定性输出,比如天气的阴晴、人的好坏,文本分类、图片识别 其间是没有大小关系的
1.3 数据的特征、样本和标签
特征和标签很容易理解
什么是样本,其实就是特征加标签,其数量和标签数相同
1.4 训练数据和测试数据
解释的想法都没有
1.5 机器学习的建模流程
流程:
DataSource-->数据预处理-->特征工程-->建模-->验证
一般花大量时间在数据预处理和特征工程(提取出有价值的特征)
特征工程结束后,特征一般被做成张量的形式,以便输入模型,建模
(检测哪个模型好,调参,改造,调参...),验证(也很重要,重要的是验证的指标--评估标准)
如何解决甚至跳过特征工程是机器学习最大的挑战和难题,才有了深度学习的抬头
建模技巧:数据可视化,建模以前要对样本数据进行透彻的了解
如何可视化:1.没有办法,特征太多 2. 降维(PCA) 3.对每一个特征分别进行可视化,发现他们之间的联系
为什么要将数据可视化,是为了发现数据的特点,从而更好的建模。
发现数据的特点很重要,发现数据的特点很重要,发现数据的特点很重要,发现数据的特点很重要,发现数据的特点很重要,发现数据的特点很重要,所以重视可视化,所以重视可视化,所以重视可视化,所以重视可视化,所以重视可视化,所以重视可视化,所以重视可视化,所以重视可视化,所以重视可视化,所以重视可视化,所以重视可视化,所以重视可视化。
数据探索(data exploration)阶段我们通过数据可视化,试图从直观的角度来查看数据的特性,比如数据的分布是否满足线性的? 数据中是否包含异常值?特征是否符合高斯分布等等
为什么分析数据呢,因为要查看数据符合什么特性,符合什么分布(,早期的机器学习、人工智能是统计学开的,惊不惊讶,没有计算机人的事)然后采取什么模型。
再怎么强调分析数据,也不过分
(PS:一篇好的论文,也强调对实验结果的分析,特别是对评估标准的分析)
一些基础概念:
1.交叉验证
2.特征缩放
3.降维
4.介绍一些图片的基础特征概念
5.缺失值的处理
6.特征编码技术
7.复杂度分析
8.交叉熵及其目标函数
9.随机梯度
10 什么是过拟合
11.模型的泛化以及过拟合
12.L1与L2正则
13.正则和最大后验概率
14.深度学习中评价指标:准确率、精确率、召回率、 F-1 Score、ROC、AUC、MAE
15.特征选择常用算法
https://blog.csdn.net/wangdong2017/article/details/82226763
16..生成模型和判别模型
https://blog.csdn.net/u010358304/article/details/79748153
17.不确定性和信息增益
18.对于连续性特征的处理
19.评估标准 准确率
20.特征工程技术
https://blog.csdn.net/hellozhxy/article/details/82686572
21.基于残差的训练方式
22.不平衡样本的处理
23.ROC与AUC
24.聚类算法的评估标准
25.数字化营销场景
26.RFM模型和用户分层
27.层次聚类与交叉验证
28.从上到下和从下到上的层次聚类
29.层次聚类与距离计算
30.协同过滤
31.隐变量模型与矩阵分解算法
32.矩阵分解的优化问题
33.各种激活函数
二 实战阶段
1.简单线性回归模型测试
2. KNN最邻近算法
3.线性回归
4.逻辑回归
5.正则
6.朴素贝叶斯
7.决策树
8.随机森林
9.提升树
10.K-means
11.层次聚类
12.协同过滤
13.SVM
14.神经网络
什么是广义线性模型
指数族分布即为广义线性模型的概率分布
线性回归什么是最重要的,是目标函数(损失函数)
为什么说损失函数很重要,因为我们采用的是梯度下降法,必须要保证下降至最低点,由最小二乘法确定的损失函数,经过数学论证,可以确保达到最低点。
由最小二乘法得出的损失函数,经过数学证明可以直接通过公式得出其最优的参数
经过对线性回归的学习,一般人都会有一种普遍错误(夸张了一点,应该是很片面)的直觉认知,那就是认为
线性回归模型假设输入数据和预测结果遵循一条直线的关系
如下图所示:
自变量(特征 x)和因变量(结果 y)的关系是一条直线
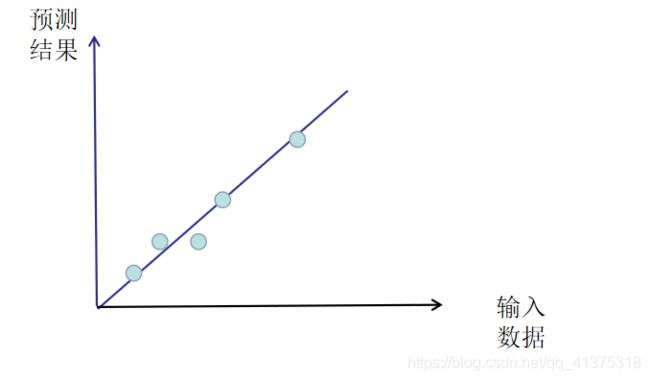
对线性含义要理解的透彻需要从其定义入手:
线性函数的定义是:多元一阶(零)多项式
我们最熟悉的就是,只有一个变量的单项式,f(x) = a + bx,这就直接导致了我们对线性相关的理解为一条直线,
实际上线性函数的一般定义为:
![]()
在二维平面上由x、y轴组成
由泰勒公式
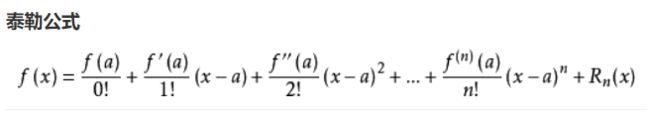
可知如果输入一元参数标量x,那么一元多阶多项式可以表示在二维平面上的任意函数,即任意曲线。
接下来就是比较骚的操作:
一元多阶多项式可转化为多元一阶多项式
一般的线性函数是这样的:
图1:
对线性函数含义有了一定的理解后就是要对 线性回归模型 要理解清楚
线性回归模型是:利用线性函数对一个或多个自变量和因变量(y)之间的关系进行拟合的模型。
即输入数据进过线性函数后的输出要与真实值接近,如果接近的好,就是好的线性回归模型,即好的线性函数,否则就是差的模型。
假设在进过输入数据训练以后,我们得出系数为【1000,100,20,5,-5,-2,9,-250,253】的线性模型函数:
y=1000X1+100X2+20X+3+5X4-5X5-2X6+9X7-250X8+253
(即图1所示:)
如果与真实数据的拟合情况如下图所示,即是好模型:

如果与真实数据的拟合情况如下图所示,即是坏模型:

具体衡量标准即为cost function(衡量真实值和预测值之间的差距,差距小就是好模型)
…
我就没想过讲这么细!!!
…
什么是线性回归?
线性回归就是通过线性函数输出一个值,值的大小不固定
以下是比较重要的,线性回归的目的是什么?
线性回归的目的就是是构建一个好的线性模型,就是构建一个好的线性函数,就是要得到好的系数,就是要有一个好的输出值。
以达到现实生活中的想要结果,比如通过输入数据,得出你将来的身高;输入数据,得出你将来的工资;输入数据,得到你的另一半会有多高。
