从线性回归入门机器学习与深度学习
以前想学深度学习,总觉得高大上,想入门但是总觉得特别麻烦,学过一点点机器学习之后再看李沐老师的深度学习,感觉现在稍稍入门了,现在整理一下看看
深度学习是包含在机器学习中的,重点是神经网络,是从感知机开始发展的(没记错的话),但是直接上感知机可能会一脸迷糊,所以我决定用机器学习中的线性回归开始整理
注意:本文不包含代码
机器学习
个人理解:机器学习是指,用一些已经发生过的事情所产生的数据和结果,预测以后在满足某些要求后会发生的结果
举个例子:
训练数据:我的汽车的油量达到红线了,然后从家里驶向加油站,到达加油站就刚好没油了;我的汽车油量达到红线了,然后从学校驶向加油站,到达加油站还有油.
训练:这种事情发生了几十次
预测:今天我的汽车油量达到红线了,我在家,我到达加油站时车里还有没有油?
这个例子并不够形象(据说西瓜书里有很多很形象的例子但是我还没看),不过也可以试着说明一点问题了
在这个例子里面,我有几个变量(机器学习里面称呼为特征):油量(达到红线),地点(家,学校),有一个预测结果(到达加油站的油量),所以可以大致做一个预测
不过现实问题中的特征不是这么简单的,比如,车的重量不同耗油量也不同,还有交通状况,然后"到达红线"也太模糊了.除此以外,还有一些参数也许无关紧要,比如汽车颜色,车灯坏没坏等等
简单线性回归的解释
线性回归是机器学习的方法之一,解决回归问题,比较经典的是波士顿房价预测问题
其实本质是函数问题,举个最简单的问题:汽车的速度是30km/h,预测汽车五小时后已经行驶的距离,其实直接可以写出来:距离y=305=150(km),预测用的公式也很简单:距离=30t(t是时间)
但是汽车可能还受到红绿灯的影响,平均一个红绿灯要让汽车停3分钟(路比较堵),那么预测用公式就是距离y=30t-0.05n(t是时间,n是红绿灯个数)
但是汽车可能还受道路情况影响…
但是汽车可能还…
…
所以我们假设,汽车行驶的距离 y = k 1 x 1 + k 2 x 2 + . . . + k n x n + b y=k_1x_1+k_2x_2+...+k_nx_n+b y=k1x1+k2x2+...+knxn+b,其中 x 1 x_1 x1是时间, x 2 x_2 x2是红绿灯个数等等
然后我们可以发现,不同的汽车和路况, x 1 , x 2 . . . x n x_1,x_2...x_n x1,x2...xn不一样,但是 k 1 , k 2 , . . . k n k_1,k_2,...k_n k1,k2,...kn差不多(如果差很多,那么肯定是某个特征你没有考虑进去),所以我们可以把差不多的和差得多的分开,也就是线性代数中的向量乘法:
y = K X + b , 其 中 K = [ k 1 , k 2 , . . . , k n ] , X = [ x 1 x 2 . . . x n ] y=KX+b,其中K=[k_1,k_2,...,k_n],X=\begin{bmatrix} x_1\\x_2 \\... \\x_n \end{bmatrix} y=KX+b,其中K=[k1,k2,...,kn],X=⎣⎢⎢⎡x1x2...xn⎦⎥⎥⎤(向量乘法)
当然写法没有限制,你写k写w都一样,这样一来,理论上求出 K K K,我们就知道一辆车多久可以走多远了
现在问题来了,怎么求 K , b K,b K,b呢?
(你要是和我说待定系数法小心我打你哦)
我刚刚举的例子是一个线性很强的,所以肯定有人觉得可以用待定系数法来直接求方程,但是现实中,我们的数据不会这么好,比如,驾驶人的速度不会一直精准的卡在30km/h,车也不会一直走完全相同的路线,可能向右偏一点让别人超车,可能向左偏一下让一让电动车…
理论上的函数图像:

实际上的函数:

所以不能用待定系数法,这也是为什么要用机器学习
损失函数
在上面两个图中,红色的线理论上是我们预测出来的方程,也就是我们要求的内容,而点则是我们已有的数据,纵轴是路程y,横轴是X
因为高纬度的情况不好可视化,所以我就用二维图像随便画了以下
在这里,我们可以看到,有很多点其实并不在红色的线上,也就是说,我们要是真的算出来了一个方程 f ( X ) f(X) f(X),也不会出现 y = f ( X ) y=f(X) y=f(X)对所有的X都有效这种情况,即机器学习算出来的也只是一个大致的结果,这是因为"噪音",也就是各种各样的因素导致的与结果的偏差(不可避免)
我们把这部分偏差记录下来,称之为损失,损失 L o s s = ∑ i = 1 m ∣ y − f ( X ) ∣ Loss=\sum_{i=1}^m|y-f(X)| Loss=∑i=1m∣y−f(X)∣(注意,这里 f ( X ) f(X) f(X)还没有求出来,另外损失也不能用负数表示)
当然损失不止这一种求法,比如两点间的距离: L o s s = ∑ i = 1 m ( y − f ( X ) ) 2 Loss=\sum_{i=1}^m\sqrt{(y-f(X))^2} Loss=∑i=1m(y−f(X))2
如果我们已经尽可能地考虑了可能的特征,那么我们受到的噪音就是完全随机的,应该是满足正态分布的(具体的数学原理我不太清楚,可能也记错了)
如果我们要尽可能准确的预测,就是要损失尽可能小,也就是求损失函数
L o s s = ( y − f ( X ) ) 2 = ( y − K X − b ) 2 Loss=\sqrt{(y-f(X))^2}=\sqrt{(y-KX-b)^2} Loss=(y−f(X))2=(y−KX−b)2的最小值
到这里,其实已经可以试着直接求解了,网上也有,多元线性回归的正规方程解
梯度法
如果给你一个这样的图像,并告诉你它的方程 f ( x ) f(x) f(x):

你要怎么求最小值呢?
如果 f ( x ) f(x) f(x)是一元二次方程,可以直接套公式,如果是更复杂的方程,那就只有一个个尝试了
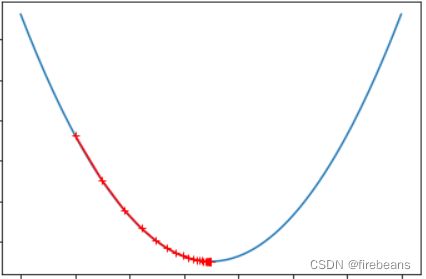
一个点一个点地挪动,直到挪动到怎么挪都不会变得更小了,大致就可以认为我们到达最低点了,些许误差可以理解
但是要怎么确定方向呢?
别和我说两头都试试就成这种话,二维空间是只有两头,但是别忘了我们要算的不是二维,不是只有一个x的一次函数,而且方向可能是会随时变化的:

这样的话一个个尝试方向会变得很复杂
因此有人提出来了,按照梯度的方向来确定移动方向,高数基础不好的同学可以理解为求导,可以看出来,每个点的导数*(-1),指向的就是最小值的方向(在这个图里,正方向是向右,负方向是向左)
所以可以用梯度来确定步长,随着接近最小值,梯度也开始减小(变得平缓),步长变小,更好确定最低点
那么求方程 f ( x ) f(x) f(x)的最小值,就变成了逐一尝试 x = x − f ′ ( x ) x=x-f'(x) x=x−f′(x),然后算 f ( x ) f(x) f(x)直到其达到最小
为了防止出现步子迈太大导致无法到达最小值

可以给梯度加一个参数: x − η f ′ ( x ) x-\eta f'(x) x−ηf′(x),在机器学习中称呼 η \eta η为学习率
用 f ( x ) f(x) f(x)还是太不准确了,因为这里是二维图像,但是我们最后要解决的是多维的
所以这样写 θ − η d J d θ , 其 中 J 是 关 于 θ 的 方 程 , d J d θ 是 J 关 于 θ 的 梯 度 \theta-\eta \frac{dJ}{d\theta},其中J是关于\theta的方程,\frac{dJ}{d\theta}是J关于\theta的梯度 θ−ηdθdJ,其中J是关于θ的方程,dθdJ是J关于θ的梯度
注意:使用梯度下降法之前最好对数据进行归一化,否则部分数据值对于方程整体的影响会很大
这里不对归一化进行总结
现在回到损失函数部分,这次我们写得专业一点点
我们把损失函数用 J ( θ ) J(\theta) J(θ)表示,其中 θ \theta θ就是我们刚刚用的 K K K,因为是要求的内容所以把它当作参数,问题就变成了不断尝试 θ = θ − η d J d θ \theta=\theta-\eta \frac{dJ}{d\theta} θ=θ−ηdθdJ直到 J ( θ ) J(\theta) J(θ)最小
但是这个最小很难达到0,所以我们要先预设一个数,比如0.001,当 J ( θ ) J(\theta) J(θ)的变化小于0.001时,默认它已经最小了
其实这个梯度也可以简化:
能看懂数学推导的同学可以看一下
∇ J ( θ ) = { ∂ J ∂ θ 0 ∂ J ∂ θ 1 . . . ∂ J ∂ θ n } = 2 m ∣ ∑ i = 1 m ( X b ( i ) θ − y ( i ) ) ∑ i = 1 m ( X b ( i ) θ − y ( i ) ) ⋅ X 1 ( i ) . . . ∑ i = 1 m ( X b ( i ) θ − y ( i ) ) ⋅ X n ( i ) ∣ = 2 m ⋅ X b T ⋅ ( X b θ − y ) \nabla J(\theta)=\begin{Bmatrix} \frac{\partial J}{\partial \theta_0} \\ \frac{\partial J}{\partial \theta_1} \\ ... \\\frac{\partial J}{\partial \theta_n}\end{Bmatrix}=\frac{2}{m}\begin{vmatrix}\sum_{i=1}^{m}(X_b^{(i)}\theta -y^{(i)}) \\ \sum_{i=1}^{m}(X_b^{(i)}\theta -y^{(i)})\cdot X_1^{(i)}\\...\\ \sum_{i=1}^{m}(X_b^{(i)}\theta -y^{(i)})\cdot X_n^{(i)}\end{vmatrix} =\frac{2}{m}\cdot X_b^T\cdot (X_b\theta-y) ∇J(θ)=⎩⎪⎪⎨⎪⎪⎧∂θ0∂J∂θ1∂J...∂θn∂J⎭⎪⎪⎬⎪⎪⎫=m2∣∣∣∣∣∣∣∣∣∑i=1m(Xb(i)θ−y(i))∑i=1m(Xb(i)θ−y(i))⋅X1(i)...∑i=1m(Xb(i)θ−y(i))⋅Xn(i)∣∣∣∣∣∣∣∣∣=m2⋅XbT⋅(Xbθ−y)
θ = θ − η ∇ J ( θ ) , 再 将 θ 放 入 J ( θ ) 中 , 对 比 前 后 J ( θ ) 的 变 化 , 如 果 足 够 小 则 返 回 θ \theta = \theta - \eta \nabla J(\theta),再将\theta 放入J(\theta)中,对比前后J(\theta)的变化,如果足够小则返回\theta θ=θ−η∇J(θ),再将θ放入J(θ)中,对比前后J(θ)的变化,如果足够小则返回θ
有没有发现我们漏了啥?
我们开始的时候设置的是 y = K X + b y=KX+b y=KX+b,但是把 K K K换成 θ \theta θ后, b b b怎么办?单独再求吗?
通常我们这样设置: y = θ X , 其 中 θ = [ θ 0 , θ 1 , θ 2 , . . . , θ n ] , X = [ 1 x 1 x 2 . . . x n ] y=\theta X,其中\theta=[\theta_0, \theta_1,\theta_2,...,\theta_n],X=\begin{bmatrix} 1\\x_1\\x_2 \\... \\x_n \end{bmatrix} y=θX,其中θ=[θ0,θ1,θ2,...,θn],X=⎣⎢⎢⎢⎢⎡1x1x2...xn⎦⎥⎥⎥⎥⎤这样, θ 0 \theta_0 θ0其实就是我们的 b b b
测试
那么我们最后求出来了一个 θ = [ θ 0 , θ 1 , θ 2 , . . . , θ n ] \theta=[\theta_0, \theta_1,\theta_2,...,\theta_n] θ=[θ0,θ1,θ2,...,θn],是不是就算求出来一个可以用于预测的函数了呢?
其实不太确定,你写个普通程序都得跑跑看能不能运行,做了个机器学习拿出来就直接用肯定不稳妥,如果我们的预测不准确,万一有紧急事件,出了问题咋办?
所以我们并不会把所有的数据用于训练,而是会保留一部分数据用于测试
具体如何测试这里就不具体说明了,只贴一些注意事项:
我们获得的数据在训练之前要随机分成训练数据和测试数据
原则上测试数据只使用一次,用于测试模型的表现如何
如果想要反复训练直到"模型表现好一点",不可以用测试数据,可以将训练数据再分成两部分,一部分作为实际训练数据,一部分作为验证数据,用验证数据调整模型的表现,最后用测试数据测试一遍,具体可以在网上查询:交叉验证
贴几个评测标准
均方误差MSE= 1 m ∑ i = 1 m ( y t e s t ( i ) − y ^ t e s t ( i ) ) 2 \frac{1}{m}\sum^m_{i=1}(y_{test}^{(i)}-\widehat y_{test}^{(i)})^2 m1∑i=1m(ytest(i)−y test(i))2
均方根误差RMSE= 1 m ∑ i = 1 m ( y t e s t ( i ) − y ^ t e s t ( i ) ) 2 \sqrt{\frac{1}{m}\sum^m_{i=1}(y_{test}^{(i)}-\widehat y_{test}^{(i)})^2} m1∑i=1m(ytest(i)−y test(i))2 (误差意义更明显)
平均绝对误差MAE= 1 m ∑ i = 1 m ∣ y t e s t ( i ) − y ^ t e s t ( i ) ∣ \frac{1}{m}\sum^m_{i=1}|y_{test}^{(i)}-\widehat y_{test}^{(i)}| m1∑i=1m∣ytest(i)−y test(i)∣
R 2 = 1 − ∑ i ( y ( i ) − y ^ ( i ) ) 2 ∑ i ( y ( i ) − y ‾ ( i ) ) 2 = 1 − ∑ i ( y ( i ) − y ^ ( i ) ) 2 / m ∑ i ( y ( i ) − y ‾ ( i ) ) 2 / m = 1 − M S E ( y ^ , y ) V a r ( y ) R^2 = 1- \frac{\sum_i (y^{(i)}-\widehat y^{(i)})^2}{\sum_i (y^{(i)}-\overline y^{(i)})^2}=1- \frac{\sum_i (y^{(i)}-\widehat y^{(i)})^2/m}{\sum_i (y^{(i)}-\overline y^{(i)})^2/m}=1-\frac{MSE(\widehat y, y)}{Var(y)} R2=1−∑i(y(i)−y(i))2∑i(y(i)−y (i))2=1−∑i(y(i)−y(i))2/m∑i(y(i)−y (i))2/m=1−Var(y)MSE(y ,y) 注:Var是方差
多元线性回归
这个我只简单介绍以下
我们刚刚做的线性回归是所有的x都是一次的函数,但是现实生活中,事件的关系可能更复杂,比如部分事件与某个参数的k次方成正比等等
所以在参数里,我们的某一项参数就不可以设置为x,而是设置为 x k x^k xk
还有一堆调整和优化,防止过拟合等等操作,这里不详细介绍,并没有你想象的那么难,只不过把向量运算变成矩阵运算了
深度学习
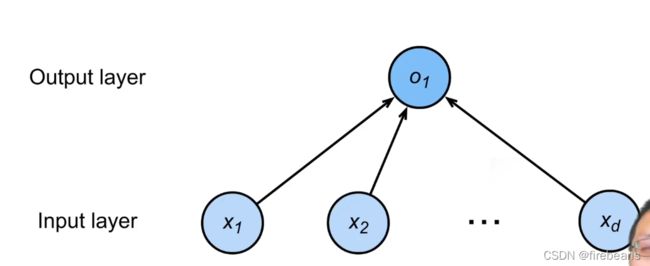
线性回归可以理解为单层神经网络,输入层是 X = [ x 1 x 2 . . . x n ] X=\begin{bmatrix} x_1\\x_2 \\... \\x_n \end{bmatrix} X=⎣⎢⎢⎡x1x2...xn⎦⎥⎥⎤输出层是一个参数 o 1 o_1 o1
那么如果输出层是三个呢?(也就是一个三维向量)

看看,有没有一点神经网络的样子了?
其实这个就是神经网络,叫做线性层
深度学习就是这种内容,感知机不过是不同的映射规律罢了
因为pytorch有很方便的使用方法,很多讲解视频直接上手用,但实际上,每一层的关系大抵是这种