【GCN-RS】经典工作：NGCF、LightGCN、LR-GCCF（代码实现）

开源了一个小项目，将一些经典的RS模型整合到一套代码中，可以作为学习参考，
GitHub地址：https://github.com/ChadsLee/RS_Zoos

NGCF：Neural Graph Collaborative Filtering (SIGIR’19)

前文GCN中的邻接矩阵$A$可以表征数据之间的关联，在这里换了一个说法，叫做“CF signal”。

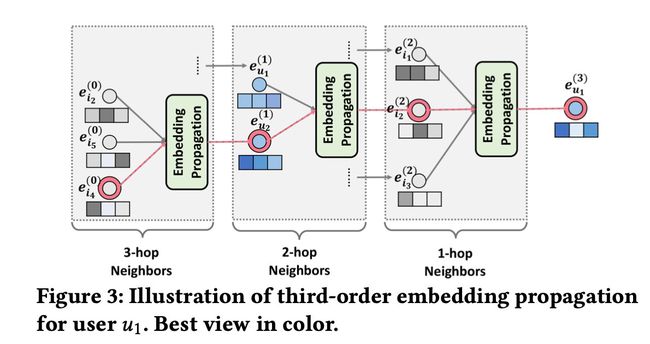
假设用户为$u$，物品为$i$，我们可以画出user-item的二部图，同时根据二部图可以将$u_1$的高维连接表示出来，如下图所示:

模型框架主要有三个部分组成：

• Embedding Layer：提供初始的user embedding 和 item embedding
• Multiple Embedding Propagation Layers：通过注入高阶连接关系来细化嵌入
• The Prediction Layer：通过整合多层嵌入来预测$(u,i)$

Embedding Layer

$$\mathbf{E}=[\underset{\text{users embeddings }}{{\mathbf{e}}_{u_1},\cdots ,{\mathbf{e}}_{u_N}},\underset{\text{item embeddings }}{{\mathbf{e}}_{i_1},\cdots ,{\mathbf{e}}_{i_M}}]$$

d维embedding，没什么好说的，如果是矩阵分解，${\mathbf{e}}_u$和${\mathbf{e}}_i$一乘就就是预测结果了。

Embedding Propagation Layers

$u->i$和$i->u$是一样的，这里以$u$为例。首先考虑一层，对应一阶的情况。

first-order propagation

物品$i$传递给消费过他的用户$u$的信息可以表达为：
$$\begin{gathered} {\mathbf{m}}_{u\leftarrow i}=f\left({\mathbf{e}}_i,{\mathbf{e}}_u,p_{ui}\right) \\ {\mathbf{m}}_{u\leftarrow i}=\frac{1}{\sqrt{\left|{\mathcal{N}}_u\right|\left|{\mathcal{N}}_i\right|}}\left({\mathbf{W}}_1{\mathbf{e}}_i+{\mathbf{W}}_2\left({\mathbf{e}}_i\odot {\mathbf{e}}_u\right)\right), \end{gathered}$$
$W_1$ 和$W_2$是训练出来的权重矩阵，维度为$d\ast d^{\prime }$，$\frac{1}{\sqrt{|{\mathcal{N}}_u||{\mathcal{N}}_i|}}$就是衰减因子$p_{ui}$。

信息聚合：
$${\mathbf{e}}_u^{(1)}=\text{ LeakyReLU }\left({\mathbf{m}}_{u\leftarrow u}+\sum _{i\in {\mathcal{N}}_u}{\mathbf{m}}_{u\leftarrow i}\right)$$
到这里为止，形式上和GCN里的$AXW$差的比较多，但是在思想上是相同的，用周围的点先更新一下自己，只不过计算方法有些差别。

high-order propagation

$$\begin{gathered} \{\begin{array}{l}{\mathbf{m}}_{u\leftarrow i}^{(l)}=\frac{1}{\sqrt{|{\mathcal{N}}_u||{\mathcal{N}}_i|}}\left({\mathbf{W}}_1^{(l)}{\mathbf{e}}_i^{(l-1)}+{\mathbf{W}}_2^{(l)}\left({\mathbf{e}}_i^{(l-1)}\odot {\mathbf{e}}_u^{(l-1)}\right)\right)\\ {\mathbf{m}}_{u\leftarrow u}^{(l)}={\mathbf{W}}_1^{(l)}{\mathbf{e}}_u^{(l-1)}\end{array} \\ {\mathbf{e}}_u^{(l)}=\text{ LeakyReLU }\left({\mathbf{m}}_{u\leftarrow u}^{(l)}+\sum _{i\in {\mathcal{N}}_u}{\mathbf{m}}_{u\leftarrow i}^{(l)}\right) \end{gathered}$$

prediction layer

经过$L$层的传播后，不是取用户$u$最后一层的向量，而是把$L$个向量$e_u^1,\dots ,e_u^L$串联拼接起来，最终得到用户$u$的表示：
$${\mathbf{e}}_u^{\ast }={\mathbf{e}}_u^{(0)}\Vert \cdots \Vert {\mathbf{e}}_u^{(L)},{\mathbf{e}}_i^{\ast }={\mathbf{e}}_i^{(0)}\Vert \cdots \Vert {\mathbf{e}}_i^{(L)}$$
最后用向量内积得到预测结果：
$${\hat{y}}_{\mathrm{N}\mathrm{G}\mathrm{C}\mathrm{F}}(u,i)={\mathbf{e}}_u^{\ast \top }{\mathbf{e}}_i^{\ast }$$
所以NGCF的整体框架：

LightGCN（SIGIR’20）

NGCF是经典之作，但是模型似乎有些太复杂了，本文先做实验证明NGCF模型的缺陷，然后简化了NGCF。

NGCF有缺陷

文章认为非线性激活函数和特征转换对CF模型没有用，在其他结点分类任务如文本分类中，每个结点都包含丰富的特征语义，如文章摘要等，在CF任务里每个结点只有ID输入，没有丰富的特征。也做了消融实验证明：

LightGCN

图卷积的定义为：
$$\begin{array}{l}{\mathbf{e}}_u^{(k+1)}={\sum }_{i\in {\mathcal{N}}_u}\frac{1}{\sqrt{|{\mathcal{N}}_u|}\sqrt{|{\mathcal{N}}_i|}}{\mathbf{e}}_i^{(k)}\\ {\mathbf{e}}_i^{(k+1)}={\sum }_{u\in {\mathcal{N}}_i}\frac{1}{\sqrt{|{\mathcal{N}}_i|}\sqrt{|{\mathcal{N}}_u|}}{\mathbf{e}}_u^{(k)}\end{array}$$
非线性激活函数没了，特征变换矩阵没了，也不整合自身节点了。

经过$K$层后，用户、物品节点信息聚合为：
$$\begin{gathered} {\mathbf{e}}_u=\sum _{k=0}^K{\alpha }_k{\mathbf{e}}_u^{(k)}, \\ {\mathbf{e}}_i=\sum _{k=0}^K{\alpha }_k{\mathbf{e}}_i^{(k)} \end{gathered}$$
所以模型能训练的参数只有重要性权重${\alpha }_k$和第0层的embedding，作者又将${\alpha }_k=1/(k+1)$。

预测时做向量内积：
$${\hat{y}}_{ui}=e_u^T{e}_i$$

LR-GCCF (AAAI’20)

和LightGCN同年，指出了NGCF非线性激活函数的缺点（但是没有去掉特征转换），所以改进了信息聚合的方法。文章提出了残差的思想，但实际上和NGCF一模一样。

信息聚合

对于每个用户和物品，传播的矩阵形式：
$$\begin{array}{l}{\left[{\mathbf{E}}^{k+1}\right]}_u={\mathbf{e}}_u^{k+1}=\left[\frac{1}{d_u}{\mathbf{e}}_u^k+{\sum }_{j\in R_u}\frac{1}{d_j\times d_u}{\mathbf{e}}_j^k\right]{\mathbf{W}}^k\\ {\left[{\mathbf{E}}^{k+1}\right]}_i={\mathbf{e}}_i^{k+1}=\left[\frac{1}{d_i}{\mathbf{e}}_i^k+{\sum }_{u\in R_i}\frac{1}{d_i\times d_u}{\mathbf{e}}_u^k\right]{\mathbf{W}}^k\end{array}$$
其中$d_i(d_u)$代表在用户项目二分图中的item $i$(user $ u $)的diagonaldegree，$R_{*}$ 代表节点 $(\ast )$ 在图 $\mathcal{G}$ 中的邻居节点。

作者引入了残差的概念，第$k+1$层的输出等于上一层的输出加上第$k+1$层的向量内积：
$${\hat{r}}_{ui}^{k+1}={\hat{r}}_{ui}^k+<{\mathbf{e}}_u^{k+1},{\mathbf{e}}_i^{k+1}>$$
所以模型的输出就是：
$$\begin{array}{rl}{\hat{r}}_{ui}& ={\hat{r}}_{ui}^{K-1}+<{\mathbf{e}}_u^K,{\mathbf{e}}_i^K>\\ & ={\hat{r}}_{ui}^{K-2}+<{\mathbf{e}}_u^{K-1},{\mathbf{e}}_i^{K-1}>+<{\mathbf{e}}_u^K,{\mathbf{e}}_i^K>\\ & ={\hat{r}}_{ui}^0+<{\mathbf{e}}_u^1,{\mathbf{e}}_i^1>+\dots +<{\mathbf{e}}_u^K,{\mathbf{e}}_i^K>\\ & =<{\mathbf{e}}_u^0\Vert {\mathbf{e}}_u^1\Vert \dots \Vert {\mathbf{e}}_u^K,{\mathbf{e}}_i^0\Vert {\mathbf{e}}_i^1\Vert \dots \Vert {\mathbf{e}}_i^K>\end{array}$$
这就是本文标题中的“Linear Residual”，但是我们看看，它是不是其实和NGCF一模一样：
$$\begin{gathered} {\mathbf{e}}_u^{\ast }={\mathbf{e}}_u^{(0)}\Vert \cdots \Vert {\mathbf{e}}_u^{(L)},{\mathbf{e}}_i^{\ast }={\mathbf{e}}_i^{(0)}\Vert \cdots \Vert {\mathbf{e}}_i^{(L)} \\ {\hat{y}}_{\mathrm{N}\mathrm{G}\mathrm{C}\mathrm{F}}(u,i)={\mathbf{e}}_u^{\ast \top }{\mathbf{e}}_i^{\ast } \end{gathered}$$