数据结构与算法——树的进阶
树的进阶
二叉排序树
二叉排序树介绍
二叉排序树:BST: (Binary Sort(Search) Tree),对于二叉排序树的任何一个非叶子节点,要求左子节点的值比当前节点的值小,右子节点的值比当前节点的值大。
特别说明:如果有相同的值,可以将该节点放在左子节点或右子节点比如针对前面的数据(7,3,10,12,5,1,9),对应的二叉排序树为:
二叉排序树创建和遍历
一个数组创建成对应的二叉排序树,并使用中序遍历二叉排序树,比如:数组为Array(7,3,10,12,5,1,9),心创建成对应的二叉排序树为:
代码实现:
package com.iswhl.binarySortTree;
public class BinarySortTreeDemo {
public static void main(String[] args) {
int[] arr = {7,3,10,12,5,1,9};
//创建一棵二叉树
BinaryTree binaryTree = new BinaryTree();
for (int i = 0; i < arr.length; i++) {
binaryTree.add(new Node(arr[i]));
}
binaryTree.infixOrder();
}
}
//创建二叉树
class BinaryTree{
private Node root;
//添加节点
public void add(Node node){
if (this.root == null){
root = node;
}else {
root.add(node);
}
}
//树的中序遍历
public void infixOrder(){
if (root == null){
return;
}else {
root.infixOrder();
}
}
}
//创建节点
class Node{
int value;
Node left;
Node right;
public Node(int value) {
this.value = value;
}
@Override
public String toString() {
return "Node{" +
"value=" + value +
'}';
}
//添加节点
public void add(Node node){
if (node == null){
return;
}
if (node.value < this.value){//说明此时要加入树的值比当前的节点的值要小
if (this.left == null){
this.left = node;
}else {
//递归向左子树中添加节点
this.left.add(node);
}
}else {//说明要加入的节点大于,当前的节点
if (this.right == null){
this.right = node;
}else {
this.right.add(node);
}
}
}
//中序遍历
public void infixOrder(){
if (this.left != null){
this.left.infixOrder();
}
System.out.println(this);
if (this.right != null){
this.right.infixOrder();
}
}
}
二叉排序树的删除
二叉排序树的删除情况比较复杂,有下面三种情况需要考虑
1)删除叶子节点(比如:2,5,9,12)
2)删除只有一颗子树的节点(比如:1)
3)删除有两颗子树的节点.(比如: 7,3,10 )
思路分析:
第一种情况:
删除叶子节点(比如:2,5,9,12)思路
1)需求先去找到要删除的结点targetNode
(2)找到targetNode的父结点parent
(3)确定targetNode是parent的左子结点还是右子结点
(4)根据前面的情况来对应删除
左子结点parent.left = null
右子结点parent.right = null;
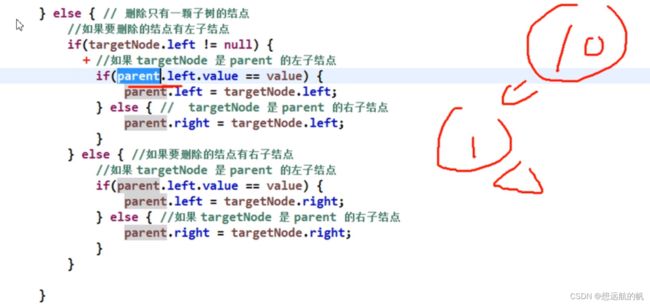
第二种情况:
删除只有一颗子树的节点比如1思路
(1)需求先去找到要册除的结点targetNode
(2)找到targetNode的父结点parent
(3)确定targetNode 的子结点是左子结点还是右子结点
(4) targetNode是parent的左子结点还是右子结点
(5)如果targetNode有左子结点
5.1如果targetNode是parent的左子结点parent.left = targetNode.left;
5.2如果targetNode是parent的右子结点parent.right = targetNode.left;
(6)如果targetNode有右子结点
6.1如果targetNode是parent的左子结点
parent.left = targetNode.right;
6.2如果targetNode是parent 的右子结点
parent.right = targetNode.right
情况三:
册除有两颗子树的节点.(比知:7,3,10 )思路
1)需求先去找到要删除的结点targetNode
(2)找到targetNode的父结点parent
(3)从targetNode 的右子树找到最小的结点
(4)用一个临时变量,将最小结点的值保存temp = 11
(5)删除该最小结点
(6) targetNode.value = temp
代码实现:
import jdk.nashorn.internal.ir.IfNode;
import sun.reflect.generics.tree.Tree;
import java.awt.print.Pageable;
public class BinarySortTreeDemo {
public static void main(String[] args) {
int[] arr = {7, 3, 10, 12, 5, 1, 9, 2};
BinarySortTree binarySortTree = new BinarySortTree();
for (int a : arr) {
binarySortTree.add(new Node(a));
}
binarySortTree.getRoot().infixOrder();
// 测试删除
System.out.println("删除节点后");
// 测试删除叶子节点
/*binarySortTree.delNode(5);
*/
// 测试删除 只有一个子节点的节点
//binarySortTree.delNode(1);
// 测试删除 只有两个子节点的节点
binarySortTree.delNode(10);
binarySortTree.getRoot().infixOrder();
}
}
// 创建二叉排序树
class BinarySortTree{
private Node root;
public void add(Node node){
if (root == null){
root = node;
}else {
root.add(node);
}
}
// 删除节点
public void delNode(int value) {
if (root == null){
return;
}else {
// 1 先去找到要删除的节点 targetNode
Node targetNode = search(value);
if (targetNode == null){ //没有找到
return;
}
// 如果这颗二叉树只有一个 targetNode 节点
if (root.left == null && root.right == null){
root = null;
return;
}
// 去找到targetNode的父节点
Node parent = searchParent(value);
// 如果要删除的节点是叶子节点 左节点? 右节点
if (targetNode.left == null && targetNode.right == null){
if (parent.value > value){
parent.left = null;
}else {
parent.right = null;
}
}else if(targetNode.right != null && targetNode.left != null){ // 要删除的节点左右都有子节点
int min = delRightTreeMin(targetNode);
targetNode.value = min;
}else { // 删除只有一颗子树的接单
// 如果要删除的这个节点有左子节点
if (targetNode.left != null){
if (parent.left.value == targetNode.value){// 如果targetNode是parent的左子节点
parent.left = targetNode.left;
}else {//如果targetNode是parent的右子节点
parent.right = targetNode.left;
}
}else {
if (parent.left.value == targetNode.value){// 如果targetNode是parent的左子节点
parent.left = targetNode.right;
}else { //如果targetNode是parent的右子节点
parent.right = targetNode.right;
}
}
}
}
}
/**
* 找到要删除的节点的右子节点开始的最小节点(右子节点的向左走) 返回该节点的值 删除该节点
* @param node 传入要删除的节点
* @return 返回从要删除的节点的右子节点开始的最小节点(右子节点的向左走)
*/
public int delRightTreeMin(Node node){
Node target = node.right;
while ( target.left != null){
target = target.left;
}
// 删除最小节点
delNode(target.value);
// 返回最小节点的值
return target.value;
}
// 查找要删除的节点
public Node search(int value){
if (root == null){
return null;
}else {
return root.search(value);
}
}
//查找父节点
public Node searchParent(int value){
if (root == null){
return null;
}else {
return root.searchParent(value);
}
}
public Node getRoot() {
return root;
}
public void setRoot(Node root) {
this.root = root;
}
// 中序遍历
public void infixOrder(){
if (root == null){
System.out.println("当前二叉排序树为空 无法遍历");
}else {
root.infixOrder();
}
}
}
// 创建节点
class Node{
int value;
Node left;
Node right;
public Node(int value) {
this.value = value;
}
public Node() {
}
/**
* 查找要删除的节点
* @param value 希望删除的节点
* @return 如果找到返回该节点 否则返回null
*/
public Node search (int value){
if (value == this.value) { // 找到就是该节点
return this;
}else if (value < this.value){
if(this.left != null){
return left.search(value);
}else {
return null;
}
}else {
if(this.right != null){
return this.right.search(value);
}else {
return null;
}
}
}
/**
* 查找要删除节点的父节点
* @param value 希望删除的节点
*/
public Node searchParent(int value){
if (this.left != null && this.left.value == value){
return this;
}else if(this.right != null && this.right.value == value){
return this;
}else {
// 如果查找的值 小于当前节点的值 , 并且当前的节点左子节点不为空
if(value < this.value && this.left != null){
return this.left.searchParent(value);
}else if(value >= this.value && this.right != null){
return this.right.searchParent(value);
}else {
// 真的找不到了 没有父节点
return null;
}
}
}
// 添加节点的方法
// 递归添加节点
public void add(Node node){
if (node == null){
return;
}
if(this.value > node.value){
if (this.left != null){
this.left.add(node);
}else {
this.left = node;
}
}else { // 如果value相等 也走右边节点
if (this.right != null){
this.right.add(node);
}else {
this.right = node;
}
}
}
// 中序遍历
public void infixOrder(){
if(this.left != null){
this.left.infixOrder();
}
System.out.print(this.value+" ");
if (this.right != null){
this.right.infixOrder();
}
}
}
package com.iswhl.binarySortTree;
public class BinarySortTreeDemo {
public static void main(String[] args) {
int[] arr = {7,3,10,12,5,1,9,2};
//创建一棵二叉树
BinaryTree binaryTree = new BinaryTree();
for (int i = 0; i < arr.length; i++) {
binaryTree.add(new Node(arr[i]));
}
System.out.println("输出原来的二叉树");
binaryTree.infixOrder();
binaryTree.delNode(1);
System.out.println("删除后的二叉树");
binaryTree.infixOrder();
}
}
//创建二叉树
class BinaryTree{
private Node root;
//添加节点
public void add(Node node){
if (this.root == null){
root = node;
}else {
root.add(node);
}
}
//查找要删除的节点
public Node search(int value){
if (root == null){
return null;
}else {
return root.search(value);
}
}
//查找要删除的父节点
public Node searchParent(int value){
if (root == null){
return null;
}else {
return root.searchParent(value);
}
}
//删除节点
public void delNode(int value){
if (root == null){
return;
}else {
//1.先找到要删除的节点
Node targetNode = search(value);
//如果没有找到要删除的节点
if (targetNode == null){
return;
}
//2.如果这颗二叉树只有一个节点
if (root.right == null && root.left == null){
root = null;
return;
}
//3.找到要删除节点的父节点
Node parent = searchParent(value);
//4.如果要删除的节点是叶子节点
if (targetNode.left == null && targetNode.right == null){
//判断targetNode是父节点的左节点还是右节点
if (parent.left != null && parent.left.value == value){
parent.left = null;
}else if (parent.right != null && parent.right.value == value){
parent.right = null;
}else if(targetNode.right != null && targetNode.left != null){ // 要删除的节点左右都有子节点
int min = delRightTreeMin(targetNode.right);
targetNode.value = min;
}else { // 删除只有一颗子树的接单
// 如果要删除的这个节点有左子节点
if (targetNode.left != null){
if (parent != null){
if (parent.left.value == value){// 如果targetNode是parent的左子节点
parent.left = targetNode.left;
}else {//如果targetNode是parent的右子节点
parent.right = targetNode.left;
}
}else {
root = targetNode.left;
}
}else {
if (targetNode.left != null){
if (parent.left.value == value){// 如果targetNode是parent的左子节点
parent.left = targetNode.right;
}else { //如果targetNode是parent的右子节点
parent.right = targetNode.right;
}
}else {
root = targetNode.left;
}
}
}
}
}
}
/**
* 找到要删除的节点的右子节点开始的最小节点(右子节点的向左走) 返回该节点的值 删除该节点
* @param node 传入要删除的节点
* @return 返回从要删除的节点的右子节点开始的最小节点(右子节点的向左走)
*/
public int delRightTreeMin(Node node){
Node target = node.right;
while ( target.left != null){
target = target.left;
}
// 删除最小节点
delNode(target.value);
// 返回最小节点的值
return target.value;
}
//树的中序遍历
public void infixOrder(){
if (root == null){
return;
}else {
root.infixOrder();
}
}
}
//创建节点
class Node{
int value;
Node left;
Node right;
public Node(int value) {
this.value = value;
}
@Override
public String toString() {
return "Node{" +
"value=" + value +
'}';
}
//查找节点的方法
/**
* 查找要删除的节点
* @param value 希望删除的节点
* @return 如果找到返回该节点 否则返回null
*/
public Node search (int value){
if (value == this.value) { // 找到就是该节点
return this;
}else if (value < this.value){
if(this.left != null){
return left.search(value);
}else {
return null;
}
}else {
if(this.right != null){
return this.right.search(value);
}else {
return null;
}
}
}
//查找要删除节点的父节点
public Node searchParent(int value){
//如果当前节点的下一个节点不为空,且下一个节点的值就是要找的节点,
//则返回当前的节点(当前的节点就是该节点的父节点)
if ((this.left != null && this.left.value == value)||
(this.right != null && this.right.value == value)){
return this;
}else {
//如果当前节点的值小于 要查找的值 则向左递归
if (this.left != null && this.value > value){
return this.left.searchParent(value);
}else if (this.right != null && this.value <= value){//大于当前值则右递归
return this.right.searchParent(value);
}else {//否则没有找到该值
return null;
}
}
}
//添加节点
public void add(Node node){
if (node == null){
return;
}
if (node.value < this.value){//说明此时要加入树的值比当前的节点的值要小
if (this.left == null){
this.left = node;
}else {
//递归向左子树中添加节点
this.left.add(node);
}
}else {//说明要加入的节点大于,当前的节点
if (this.right == null){
this.right = node;
}else {
this.right.add(node);
}
}
}
//中序遍历
public void infixOrder(){
if (this.left != null){
this.left.infixOrder();
}
System.out.println(this);
if (this.right != null){
this.right.infixOrder();
}
}
}
二叉排序树的注意事
如果删除的数10这个根节点 走到这一步时 会报空指针异常 所以需要加一个判断
平衡二叉树(AVl树)
看一个案例(说明二叉排序树可能的问题)
给你一个数列{1,2,3,4,5,6},要求创建一颗二叉排序树(BST),并分析问题所在.

基本介绍
1)平衡二叉树也叫平衡二叉搜索树(Self-balancing binary search tree)又被称为AVL树,可以保证查询效率较高。
2)具有以下特点:它是一棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树。平衡二叉树的常用实现方法有红黑树、AVL、替罪羊树、Treap、伸展树等。
3)举例说明,看看下面哪些AVL树,为什么?
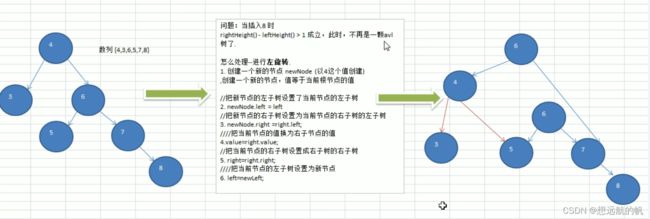
平衡二叉树的左旋转(实现思路):
问题:当插入8时
rightHeight()- leftHeight() >1成立,此时,不再是—颗avl树了.
怎么处理–进行左旋转.
1.创建一个新的节点newNode(以4这个值创建),创建一个新的节点,值等于当前根节点的值
//把新节点的左子树设置了当前节点的左子树
2.newNode.left = left
//把新节点的右子树设置为当前节点的右子树的左子树
3.newNode.right =right.left;
l//把当前节点的值换为右子节点的值
4.value=right.value;
//把当前节点的右子树设置成右子树的右子树
5.right=right.right;
//把当前节点的左子树设置为新节点
6.left=newLeft;
代码实现:
//左旋转
public void leftRotate(){
//以当前根节点的值来创建一个新的节点
//value 此时的value为当前根节点的值
//这里的newNode就后面比被当作原来的根节点
//value后面会当成根节点
Node newNode = new Node(value);
//把新节点的左子树,设置为当前节点的左子树
newNode.left = left;
//新节点的右子树为,当前节点的右子树的左子树
newNode.right = right.left;
//把当前节点的值替换为当前节点右节点的值
value = right.value;//旋转后的根节点
//把当前节点的右子树的值,替换为当前节点右节点的右节点
right = right.right;//旋转后的根节点的右节点
//把当前节点的左子树设置为新的节点
left = newNode;//旋转后的根节点的左节点
}
平衡二叉树的右旋转(实现思路):
问题:
数列{10,12,8,9,7,6}当插入6时
leftHeight( -rightHeight() >1成立,此时,不再是—颗av树了.怎么处理–进行右旋转.[就是降低左子树的高度],这里是将9这个节点,通过右旋转,到右子树
1.创建一个新的节点newNode(以10这个值创建),创建―个新的节点,值等于当前根节点的值
//把新节点的右子树设置了当前节点的右子树
2.newNode.right =right
//把新节点的左子树设置为当前节点的左子树的右子树
3.newNode.left=leftright;
//把当前节点的值换为左子节点的值
4.value=left.value;
//把当前节点的左子树设置成左子树的佐子树
5.left=left.left;
//把当前节点的右子树设置为新节点
6.right=newLeft;
代码实现:
//右旋转
public void rightRotate(){
Node newNode = new Node(value);
newNode.right = right;
newNode.left = left.right;
value = right.value;
left = left.left;
right = newNode;
}
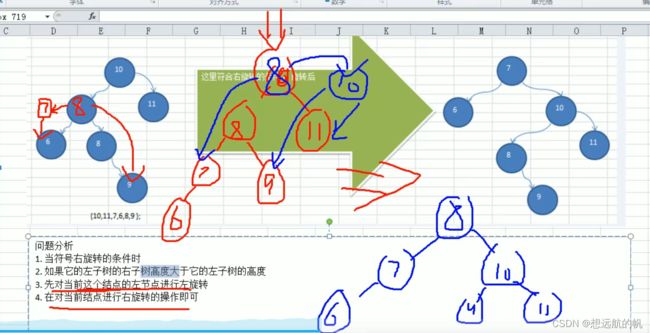
平衡二叉树的双旋转(实现思路):
代码实现:
if(rightHeight() - leftHeight() > 1){
//如果当前树的右子树的左子树的高度大于他的右子树的右子树的高度
if (right != null && right.leftHeight() > right.rightHeight()){
//先将其右子节点进行右旋转
right.rightRotate();
//再将其根节点左旋转
leftRotate();
}else {
//否则直接左旋转
leftRotate();
}
return;//必须要 用来减少不必要的判断,与防止下面的代码执行
}
if (leftHeight() - rightHeight() > 1){
//如果其左子树的右子树的高度大于其左子树的左子树的高度
if (left != null && left.rightHeight() > left.leftHeight()){
//先将其进行左旋转
left.leftRotate();
//再进行右旋转
rightRotate();
}else {
rightRotate();
}
}
全部代码:
package com.iswhl.avl;
public class AvlTreeDemo {
public static void main(String[] args) {
//int[] arr = {4,3,6,5,7,8};
//int[] arr = {10,12,8,9,7,6};
int[] arr = {10,11,7,6,8,9};
//将数组插入到Avl树中去
AvlTree avlTree = new AvlTree();
for (int i = 0; i < arr.length; i++) {
avlTree.add(new Node(arr[i]));
}
System.out.println("中序遍历树为:");
avlTree.infixOrder();
System.out.println("此时旋转后的树的高度为:"+avlTree.getRoot().height());
System.out.println("其左子树的高度为:"+avlTree.getRoot().leftHeight());
System.out.println("其右子树的高度为:"+avlTree.getRoot().rightHeight());
}
}
//创建AVL树
class AvlTree{
private Node root;
public Node getRoot() {
return root;
}
public void setRoot(Node root) {
this.root = root;
}
//添加节点
public void add(Node node){
if (this.root == null){
root = node;
}else {
root.add(node);
}
}
//查找要删除的节点
public Node search(int value){
if (root == null){
return null;
}else {
return root.search(value);
}
}
//查找要删除的父节点
public Node searchParent(int value){
if (root == null){
return null;
}else {
return root.searchParent(value);
}
}
//删除节点
public void delNode(int value){
if (root == null){
return;
}else {
//1.先找到要删除的节点
Node targetNode = search(value);
//如果没有找到要删除的节点
if (targetNode == null){
return;
}
//2.如果这颗二叉树只有一个节点
if (root.right == null && root.left == null){
root = null;
return;
}
//3.找到要删除节点的父节点
Node parent = searchParent(value);
//4.如果要删除的节点是叶子节点
if (targetNode.left == null && targetNode.right == null){
//判断targetNode是父节点的左节点还是右节点
if (parent.left != null && parent.left.value == value){
parent.left = null;
}else if (parent.right != null && parent.right.value == value){
parent.right = null;
}else if(targetNode.right != null && targetNode.left != null){ // 要删除的节点左右都有子节点
int min = delRightTreeMin(targetNode.right);
targetNode.value = min;
}else { // 删除只有一颗子树的接单
// 如果要删除的这个节点有左子节点
if (targetNode.left != null){
if (parent != null){
if (parent.left.value == value){// 如果targetNode是parent的左子节点
parent.left = targetNode.left;
}else {//如果targetNode是parent的右子节点
parent.right = targetNode.left;
}
}else {
root = targetNode.left;
}
}else {
if (targetNode.left != null){
if (parent.left.value == value){// 如果targetNode是parent的左子节点
parent.left = targetNode.right;
}else { //如果targetNode是parent的右子节点
parent.right = targetNode.right;
}
}else {
root = targetNode.left;
}
}
}
}
}
}
/**
* 找到要删除的节点的右子节点开始的最小节点(右子节点的向左走) 返回该节点的值 删除该节点
* @param node 传入要删除的节点
* @return 返回从要删除的节点的右子节点开始的最小节点(右子节点的向左走)
*/
public int delRightTreeMin(Node node){
Node target = node.right;
while ( target.left != null){
target = target.left;
}
// 删除最小节点
delNode(target.value);
// 返回最小节点的值
return target.value;
}
//树的中序遍历
public void infixOrder(){
if (root == null){
return;
}else {
root.infixOrder();
}
}
}
//创建节点
class Node{
int value;
Node left;
Node right;
public Node(int value) {
this.value = value;
}
@Override
public String toString() {
return "Node{" +
"value=" + value +
'}';
}
//返回左子树的高度
public int leftHeight(){
if (left == null) {
return 0;
}
return left.height();
}
//返回右子树的高度
public int rightHeight(){
if (right == null){
return 0;
}
return right.height();
}
//返回以该节点为根节点树的高度
public int height(){
//这里的方法很巧妙,我们使用递归的方法来遍历当前树的高度,
//选出左右子树中的高度最大值出来当做是该树的高度
return Math.max(left == null ? 0 : left.height(),right == null ? 0 : right.height())+1;
}
//查找节点的方法
/**
* 查找要删除的节点
* @param value 希望删除的节点
* @return 如果找到返回该节点 否则返回null
*/
public Node search (int value){
if (value == this.value) { // 找到就是该节点
return this;
}else if (value < this.value){
if(this.left != null){
return left.search(value);
}else {
return null;
}
}else {
if(this.right != null){
return this.right.search(value);
}else {
return null;
}
}
}
//查找要删除节点的父节点
public Node searchParent(int value){
//如果当前节点的下一个节点不为空,且下一个节点的值就是要找的节点,
//则返回当前的节点(当前的节点就是该节点的父节点)
if ((this.left != null && this.left.value == value)||
(this.right != null && this.right.value == value)){
return this;
}else {
//如果当前节点的值小于 要查找的值 则向左递归
if (this.left != null && this.value > value){
return this.left.searchParent(value);
}else if (this.right != null && this.value <= value){//大于当前值则右递归
return this.right.searchParent(value);
}else {//否则没有找到该值
return null;
}
}
}
//添加节点
public void add(Node node){
if (node == null){
return;
}
if (node.value < this.value){//说明此时要加入树的值比当前的节点的值要小
if (this.left == null){
this.left = node;
}else {
//递归向左子树中添加节点
this.left.add(node);
}
}else {//说明要加入的节点大于,当前的节点
if (this.right == null){
this.right = node;
}else {
this.right.add(node);
}
}
if(rightHeight() - leftHeight() > 1){
//如果当前树的右子树的左子树的高度大于他的右子树的右子树的高度
if (right != null && right.leftHeight() > right.rightHeight()){
//先将其右子节点进行右旋转
right.rightRotate();
//再将其根节点左旋转
leftRotate();
}else {
//否则直接左旋转
leftRotate();
}
return;//必须要 用来减少不必要的判断,与防止下面的代码执行
}
if (leftHeight() - rightHeight() > 1){
//如果其左子树的右子树的高度大于其左子树的左子树的高度
if (left != null && left.rightHeight() > left.leftHeight()){
//先将其进行左旋转
left.leftRotate();
//再进行右旋转
rightRotate();
}else {
rightRotate();
}
}
}
//左旋转
public void leftRotate(){
//以当前根节点的值来创建一个新的节点
//value 此时的value为当前根节点的值
//这里的newNode就后面比被当作原来的根节点
//value后面会当成根节点
Node newNode = new Node(value);
//把新节点的左子树,设置为当前节点的左子树
newNode.left = left;
//新节点的右子树为,当前节点的右子树的左子树
newNode.right = right.left;
//把当前节点的值替换为当前节点右节点的值
value = right.value;//旋转后的根节点
//把当前节点的右子树的值,替换为当前节点右节点的右节点
right = right.right;//旋转后的根节点的右节点
//把当前节点的左子树设置为新的节点
left = newNode;//旋转后的根节点的左节点
}
//右旋转
public void rightRotate(){
Node newNode = new Node(value);
newNode.right = right;
newNode.left = left.right;
value = right.value;
left = left.left;
right = newNode;
}
//中序遍历
public void infixOrder(){
if (this.left != null){
this.left.infixOrder();
}
System.out.println(this);
if (this.right != null){
this.right.infixOrder();
}
}
}
多路查找树
二叉树的问题分析
二叉树的操作效率较高,但是也存在问题,请看下面的二叉树
1)二叉树需要加载到内存的,如果二叉树的节点少,没有什么问题,但是如果二叉树的节点很多(比如1亿),就存在如下问题
2)问题1∶在构建二叉树时,需要多次进行/o操作(海量数据存在数据库或文件中),节点海量,构建二叉树时,速度有影响
3)问题2:节点海量,也会造成二叉树的高度很大。会降低操作速度.
多叉树
1)在二叉树中,每个节点有数据项,最多有两个子节点。如果允许每个节点可以有更多的数据项和更多的子节点,就是多叉树(multiway tree)
2)后面我们讲解的2-3树,2-3-4树就是多叉树,多叉树通过重新组织节点,减少树的高度,能对二叉树进行优化。
3)举例说明(下面2-3树就是一颗多叉树)
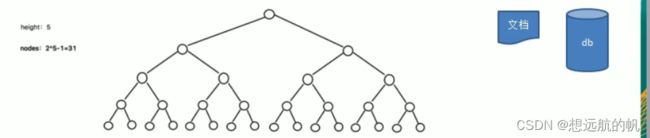
B树的基本介绍
B树通过重新组织节点,降低树的高度,并且减少i/o读写次数来提升效率。
1)如图B树通过重新组织节点,降低了树的高度
2)文件系统及数据库系统的设计者利用了磁盘预读原理,将一个节点的大小设为等于一个页(页得大小通常为4k),这样每个节点只需要一次l/o就可以完全载入
3)将树的度M设置为1024,在600亿个元素中最多只需要4次I/o操作就可以读取到想要的元素,B树(B+)广泛应用于文件存储系统以及数据库系统中
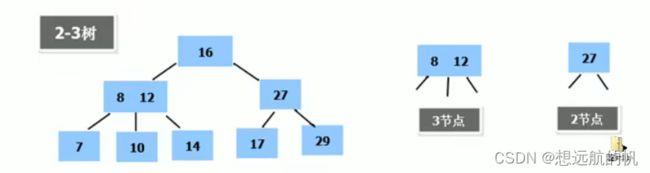
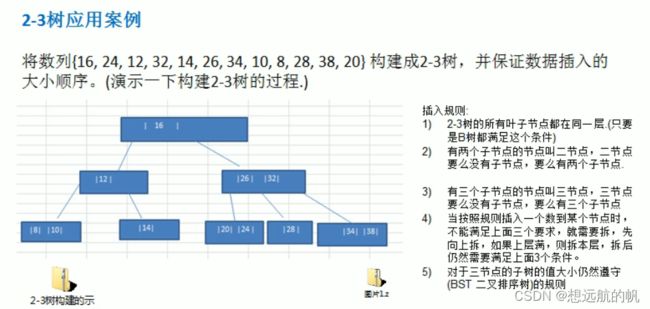
2-3树基本介绍
2-3树是最简单的B树结构,具有如下特点:
1)2-3树的所有叶子节点都在同一层.(只要是B树都满足这个条件)
2)有两个子节点的节点叫二节点,二节点要么没有子节点,要么有两个子节点.
3)有三个子节点的节点叫三节点,三节点要么没有子节点,要么有三个子节点.
4)2-3树是由二节点和三节点构成的树。
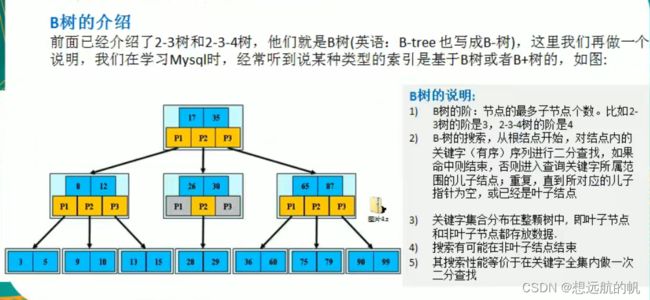
B树的介绍
B-tree树即B树,B即Balanced,平衡的意思。有人把B-tree翻译成B-树,容易让人
产生误解。会以为B-树是一种树,而B树又是另一种树。实际上,B-tree就是指的B树。
注意:B-树就是B树,没有叫做B-树的东西
B树的说明:
1)B树的阶:节点的最多子节点个数。比如2-3树的阶是3,2-3-4树的阶是4
2)B-树的搜索,从根结点开始,对结点内的关键字(有序)序列进行二分查找,如果命中则结束,否则进入查询关键字所属范围的儿子结点;重复,直到所对应的儿子指针为空,或已经是叶子结点
3)关键字集合分布在整颗树中,即叶子节点和非叶子节点都存放数据.
4)搜索有可能在非叶子结点结束
5)其搜索性能等价于在关键字全集内做一次二分查找
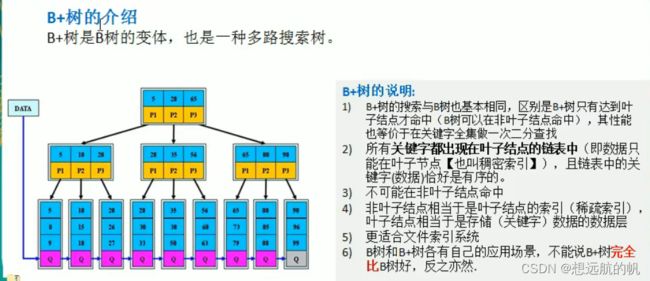
B+树的介绍
B+树的说明:
1)B+树的搜索与B树也基本相同,区别是B+树只有达到叶子结点才命中(B树可以在非叶子结点命中),其性能也等价于在关键字全集做一次二分查找
2)所有关键字都出现在叶子结点的链表中**(即数据只能在叶子节点【也叫稠密索引】)**,且链表中的关键字(数据)恰好是有序的。
3)不可能在非叶子结点命中
4)非吐子结点相当于是叶子结点的索引,(稀疏索引),叶子结点相当于是存储(关键宁)数据的数据层
5)更适合文件索引系统
6)B树和B+树各有自己的应用场景,不能说B+树完全比B树好,反之亦然.
B*树的介绍
B*树的说明:
1)B**树定义了非叶子结点关键字个数至少为(2/3)*M,即块的最低使用率为2/3,而B+树的块的最低使用率为B+树的1/2。
2)从第1个特点我们可以看出,B*树分配新结点的概率比B+树要低,空间使用率更高