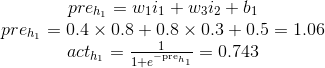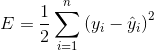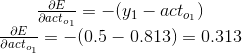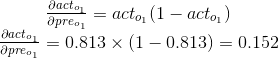scikit-learn机器学习：从感知机到人工神经网络

在本章中，我们将讨论ANN，一种可用于监督任务和非监督任务的强大非线性模型，它使用一种不同的策略来克服感知机的局限。如果将感知机类比为一个神经元，那么ANN或者说神经网络，就应该类比为一个大脑。正如一个人类的大脑由数十亿个神经元和数万亿个突触组成一样，一个ANN是一个由人工神经元组成的有向图。图的边表示权重，这些权重都是模型需要学习的参数。

本章将提供一个关于小型前馈人工神经网络结构和训练的概述。scikit-learn类库实现了用于分类、回归和特征提取的神经网络。然而，这些实现仅仅适用于小型网络。训练一个神经网络需要消耗大量的算力，在实际中大多数神经网络使用包含上千个并行处理核的图形处理单元进行训练。scikit-learn类库不支持GPU，而且在近期也没有支持的打算。GPU加速还不成熟但是在迅速的发展中，在scikit-learn类库中提供对GPU的支持将会增加许多依赖项，而这与scikit-learn项目“轻松在各种平台上安装”的目标有所冲突。另外，其他机器学习算法很少需要使用GPU加速来达到和神经网络相同的程度。训练神经网络最好使用专门的类库例如Caffe、TensorFlow和Keras来实现，而不要使用像scikit-learn这样的通用的机器学习类库。

虽然我们不会使用scikit-learn类库来训练一个用于目标识别的深度卷积神经网络（CNN）或者用于语音识别的递归网络，理解将要训练的小型网络的原理对于这些任务来说是重要的先决条件。

12.1　非线性决策边界

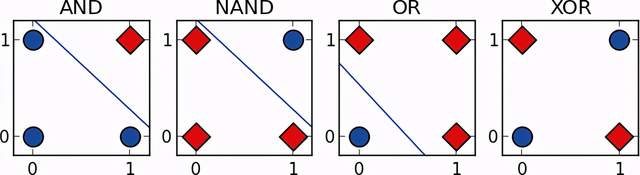
回顾第10章，虽然一些布尔函数例如AND、OR和NAND可以用感知机来逼近，线性不可分函数XOR却不能，如图12.1所示。

 

图12.1

让我们回顾XOR函数的更多细节来建立一种关于ANN能力的直觉。和AND函数（当输入都等于1时输出才等于1）以及OR函数（当输入至少有一个等于1输出才等于1）不同，只有当一个输入等于1时，XOR函数的输出才等于1。当两个条件都为真时，我们可以将XOR函数的输出看作1。第1个条件是至少有一个输出项等于1，这个条件和OR函数的检验条件相同。第2个条件是输入项不能都等于1，这个条件和NAND函数的检验条件相同。我们可以通过将输入项目同时使用OR函数和NAND函数处理，然后使用AND函数来验证两个函数的输出结果是否都等于1，来得到XOR函数的处理输出结果。也就是说，OR函数、NAND函数和AND函数可以通过组合得到和XOR函数相同的输出结果。

表12.1是关于输入A和输入B对于XOR函数、OR函数、AND函数和NAND函数的真实值表格。从这个表格中我们可以验证输入A和输入B经过OR函数的输出和NAND函数的输出再经过AND函数处理的输出结果，和直接经过XOR函数处理的输出结果相同，如表12.2所示。

 

12.2　前馈人工神经网络和反馈人工神经网络

ANN可以由3个关键组件来描述。第1个关键组件是模型的架构或者说拓扑，它描述了神经元的类型和神经元之间的连接结构。第2个关键组件是人工神经元使用的激活函数。第3个关键组件是找出权重最优值的学习算法。

ANN主要有两种类型。前馈神经网络是最常见的类型，它通过有向非循环图来定义。在前馈神经网络中，信息只在一个方向上朝着输出层进行传递。相反，反馈神经网络或者递归神经网络包含循环。反馈循环可以表示网络的一种内部状态，它会导致网络的行为基于本身的输入随着时间变化而发生变化。前馈神经网络经常用于学习一个将输入映射到输出的函数。例如，一个前馈神经网络可以被用于识别一张照片中的物体，或者预测一个SaaS产品的订阅用户流失的可能性。反馈神经网络的时间行为使其适合用于处理输入序列。反馈神经网络已经被用于在两种语言之间翻译文档和自动转录演讲。因为反馈神经网络没有在scikit-learn类库中实现，我们将把讨论的话题仅限于前馈神经网络。

12.3　多层感知机

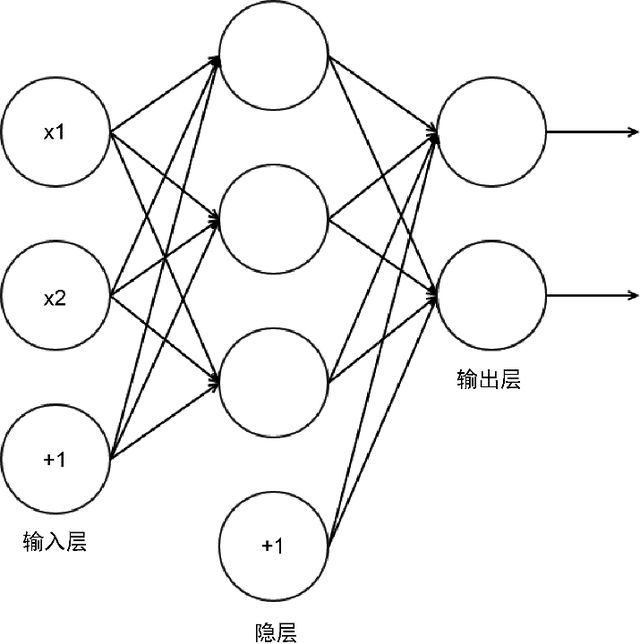
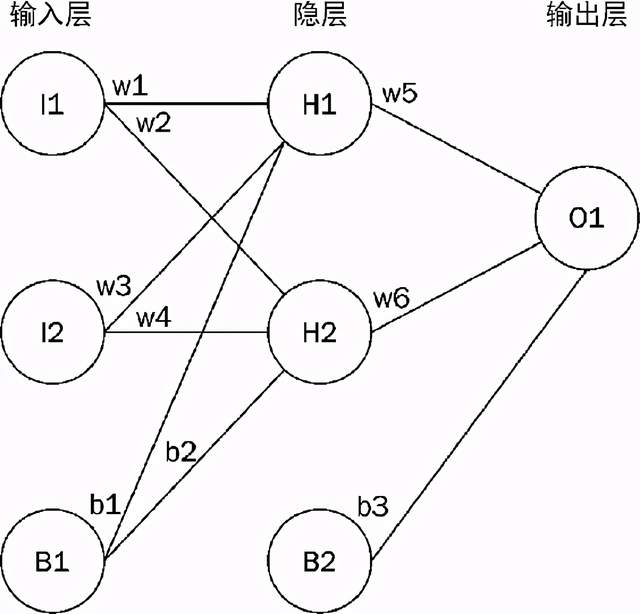
多层感知机是一个简单的ANN。然而，它的名字是一种误称。一个多层感知机的并不是每一层只包含单一的感知机的多层结构，而是一个由人工神经元模拟感知机的多层结构。多层感知机包含3层或者更多层人工神经元，这些神经元形成了一个有向、非循环图。一般地，每层和后面的层都是全连接，一个层中的每个人工神经元的输出项或者说激活项，都是下一层中每个人工神经元的输入项。特征通过输入层进行输入。输入层中的简单神经元至少和一个隐层连接。隐层表示潜在变量，这些变量在训练数据中无法被观测到。隐层中隐藏神经元通常被称为隐单元。最后一个隐层和一个输出层连接，该层的激活项是响应变量的预测值。图12.2描述了一个包含3层感知机的多层感知机结构。标有+1的神经元是常量偏差神经元，在大多数架构图中并不出现。这个神经网络有两个输入神经元，3个隐神经元以及2个输出神经元。

 

图12.2

 

输入层并不包含在一个神经网络的层数计算中，但MLPClassifier.nlayers属性的计数会包含输入层。

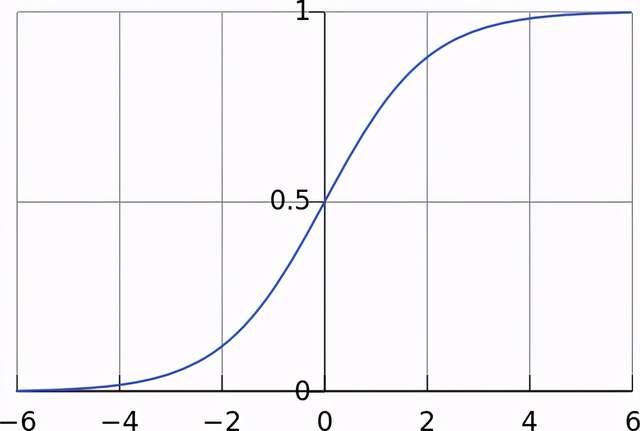
回顾第10章，一个感知机包括一个或多个二元输出、一个二元输出以及一个海维赛德阶跃激活函数。一个感知机的权重的微小变化对其输出没有影响，或者将导致输出从1变到0或者从0到1。这个特性将导致我们改变神经网络的权重时难以去理解其性能变化。正因如此，我们将使用一种不同类型的神经元创建MLP。一个S型曲线神经元包含一个或多个实值输入和一个实值输出，它使用一个S型曲线激活函数。如图12.3所示，一个S型曲线激活函数是阶跃函数的光滑版本，它在极值区间内逼近一个阶跃函数，但是可以输出0～1之间的任何值，这允许我们可以理解输入项的变化如何影响输出项。

 

图12.3

12.4　训练多层感知机

在本节内容中，我们将讨论如何训练一个多层感知机。回顾第5章，我们可以使用梯度下降法来将一个包含许多变量的实值函数C极小化。假设C是一个包含两个变量v1和v2的函数。为了理解如何通过改变变量来使C极小化，我们需要一个变量上的小变化来产生输出上的一个小变化。我们将v1值的一个变化表示为Δv1，v2值的一个变化表示为Δv2，C值的一个变化表示为ΔC。ΔC和变量变化之间的关系如公式12.1所示：

 

（公式12.1）

 

表示C对于v1的偏微分。为了方便，我们将Δv1和Δv2表示为一个向量，如公式12.2所

 

（公式12.2）

我们也将把C对每个变量的偏微分表示为C的梯度向量C，如公式12.3所示：

 

（公式12.3）

我们可以将ΔC的公式重写为公式12.4：

 

（公式12.4）

在每次迭代中，ΔC应该为负数以减小代价函数的值。为了保证ΔC为负数，我们将Δv设为公式12.5：

 

（公式12.5）

在公式12.5中，η是一个称为学习速率的超参数。我们替换Δv来阐明为什么ΔC是负数，如公式12.6所示：

 

（公式12.6）

 

的平方总是大于0，我们将其乘以学习速率，并对乘积求反。在每一次迭代中，我们都将计算C的梯度C，并更新变量在下降最快的方向上迈出一步。为了训练多层感知机，我们省略了一个重要的细节：如何理解隐单元权重的变化如何影响代价函数？更具体来说，如何计算代价函数对于连接隐层的权重的偏导数？

12.4.1　反向传播

我们已经了解了梯度下降法通过计算一个函数梯度并使用梯度来更新函数的参数来迭代地将函数极小化。为了极小化多层感知机的代价函数，我们需要计算其梯度。回顾多层感知机包含能够代表潜在变量的单元层。我们不能使用一个代价函数计算它们的误差。训练数据表明了整个网络的期望输出，但是没有描述隐单元应该如何影响输出结果。由于我们不能计算隐单元的误差，不能计算它们的梯度，或者更新他们的权重。对于该问题一种简单的解决方法是随机修改隐单元的梯度。如果一个梯度的随机变化能减少代价函数值，则该权重被更新同时评估另一个变化。即使是对于普通的网络，这个方法对算力的消耗都是非常巨大的。在本节内容中，我们将描述一种更加有效的解决方法，使用反向传播算法计算一个神经网络的代价函数针对其每一个权重的梯度。反向传播法允许我们理解每个权重如何影响误差，以及如何更新权重来极小化代价函数。

这个算法的名字是反向和传播的合成词，它指代当计算梯度时误差穿过网络层的方向。反向传播法经常和一个优化算法（例如梯度下降法）联合使用来训练前馈神经网络。理论上来说，它能用于训练包含任何数量隐单元和任何数量层的前馈网络。

和梯度下降法一样，反向传播法是一种迭代算法，每次迭代包含两个阶段。第1个阶段是向前传播或者向前传递。在向前传递阶段，输入通过网络的神经元层向前传播直到它们到达输出层。接着损失函数可以用来计算预测的误差。第2个阶段是向后传播阶段。误差从代价函数向输入传播以便每个神经元对于误差的贡献能够被估计。该过程基于链式法则，该法则能够用于计算两个或更多函数组合的导数。我们在前面已经证明了神经网络可以通过组合线性函数来逼近复杂的非线性函数。这些误差接下来可以用于计算梯度下降法需要用于更新权重的梯度值。当梯度完成更新之后，特征可以再次通过网络向前传播开始下一次迭代。

 

链式法则可以用来计算两个或者多个函数组合的导数。假设变量z依赖于y，y依赖于x。z针对x的导数可以表示为。

为了向前传播通过一个网络，我们计算在一个层中神经元的激活项，同时将激活项作为下一个层中与之连接的神经元的输入项。为了完成这些工作，我们首先需要计算出网络层中每个神经元的预激活项。回顾一个神经元的预激活项是其输入项和权重的线性组合。接着，我们通过将其激活函数应用于其预激活项上来计算出其激活项。该层的激活项会成为网络中下一层的输入项。

为了反向传播穿过网络，我们首先计算出代价函数针对最后隐层每一个激活项的偏导数。接着，我们计算最后隐层的激活项针对其预激活项的偏导数。接下来，计算最后隐层的预激活项针对其权重的偏导数，如此反复直到到达输入层。经过这个过程，我们逼近了每个神经元对于误差的贡献，同时计算出用来更新权重里那个和极小化代价函数所必需的梯度值。更具体地，对于每一层中的每一个单元，我们必须计算两个偏导数。第一个是误差针对单元激活项的偏导数。该导数不用于更新单元的权重，相反，它用于更新与该单元相连接的前面一层中的单元权重。第二，我们将计算误差针对该单元权重的导数以便更新权重值和极小化代价函数。接下来了解一个例子。我们将训练一个包含两个输入单元，一个包含两个隐单元的隐层，以及一个输出单元的神经网络，其架构图如图12.4所示。

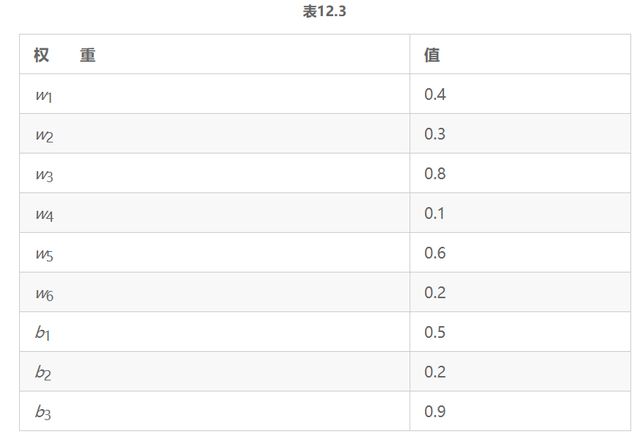
让我们假设权重的初始值如表12.3所示。

 

 

图12.4

特征向量是[0.8,0.3]，响应变量的真实值是0.5。让我们计算第一次向前传递的值，从隐单元h1开始。首先计算h1的预激活项，接着将逻辑S型曲线函数运用于预激活项计算激活项目，如公式12.7所示：

 

（公式12.7）

我们可以使用同样的过程计算h2的激活项，计算结果为0.615。接着将隐单元h1和h2的激活项目作为输出层的输入项，类似地计算出o1的激活项，计算结果为0.813。现在我们可以计算网络预测的误差。对于这个网络，我们将使用平方误差代价函数，公式如12.8所示：

 

（公式12.8）

在公式12.8中，n是输出单元的数量，

 

是输出神经元oi的激活项，yi是响应变量的真实值。我们的网络只有一个输出单元，因此n等于1。网络的预测值是0.813，响应变量的真实值是0.5，因此误差是0.313。现在我们可以更新权重w5。首先计算

 

，或者说改变w5看它如何影响误差。根据链式法则，

 

等于公式12.9：

 

（公式12.9）

也就是说，我们能够通过回答下列问题来逼近误差的变化和w5之间的联系程度。

• o1的激活项的变化能够对误差造成多大影响？
• o1预激活项的变化能对激活项o1造成多大影响？
• 权重w5的变化能对预激活项o1造成多大影响？

接着我们将从w5中减去

 

和我们的学习速率的乘积来更新权重。通过逼近误差变化和激活项o1之间的联系程度来回答第一个问题。代价函数针对输出单元激活项的偏导数如公式12.10所示：

 

（公式12.10）

接着我们通过逼近o1的激活项变化和其预激活项之间的联系程度来回答第二个问题。逻辑函数的偏导数如公式12.11所示：

 

（公式12.11）

在公式12.11中，f(x)是逻辑函数，对应的公式为1/(1+e−x)。

 

（公式12.12）

最后，我们将逼近预激活项o1的变化和w5有多大关系。预激活项是权重和输入项的线性组合，如公式12.13所示：

 

（公式12.13）

偏差项b2和

 

的导数都是0。这两项对于w5来说都是常数，w5的变化对

 

没有影响。现在我们已经回答了3个问题，我们可以计算出误差针对w5的偏导数，如公式12.14所示：

 

（公式12.14）

我们现在可以通过从w5中减去学习速率和

 

的乘积来更新w5的值。接着我我们可以遵循同样的处理方式来更新剩余的权重。完成了第一次向后传递之后，我们可以使用更新后的权重值来再次通过网络向前传播。

12.4.2　训练一个多层感知机逼近XOR函数

让我们使用scikit-learn类库训练一个网络来逼近XOR函数。我们为MLPClassifier构造函数传递activation='logistic'关键字变量来为神经元指定应该使用逻辑S型曲线激活函数。Hidden_layer_sizes参数接受一个整数元组来标明每一个隐层中的隐单元数量。我们将使用和前一节内容中相同的网络架构训练一个网络，该网络包含一个含有两个隐单元的隐层，以及一个包含一个输出单元的输出层，如代码12.1所示。

代码12.1

# In[1]:
from sklearn.model_selection import train_test_split
from sklearn.neural_network import MLPClassifier

y = [0, 1, 1, 0]
X = [[0, 0], [0, 1], [1, 0], [1, 1]]

clf = MLPClassifier(solver='lbfgs', activation='logistic',
  hidden_layer_sizes=(2,), random_state=20)
clf.fit(X, y)

predictions = clf.predict(X)
print('Accuracy: %s' % clf.score(X, y))
for i, p in enumerate(predictions):
    print('True: %s, Predicted: %s' % (y[i], p))

# Out[1]:
Accuracy: 1.0
True: 0, Predicted: 0
True: 1, Predicted: 1
True: 1, Predicted: 1
True: 0, Predicted: 0

在几次迭代之后，网络收敛。让我们来观察已经学习到的权重，并对特征向量[1,1]完成一次向前传递，如代码12.2所示。

代码12.2

# In[2]:
print('Weights connecting the input layer and the hidden layer: \n%s' %
clf.coefs_[0])
print('Hidden layer bias weights: \n%s' % clf.intercepts_[0])
print('Weights connecting the hidden layer and the output layer:
  \n%s' % clf.coefs_[1])
print('Output layer bias weight: \n%s' % clf.intercepts_[1])

# Out[2]:
Weights connecting the input layer and the hidden layer:
[[ 6.11803955  6.35656369]
 [ 5.79147859  6.14551916]]
Hidden layer bias weights:
[-9.38637909 -2.77751771]
Weights connecting the hidden layer and the output layer:
[[-14.95481734]
 [ 14.53080968]]
Output layer bias weight:
[-7.2284531]

为了向前传播，我们需要计算下列公式，如公式12.15所示。

 

 

 

 

 

 

 

 

 

 

 

（公式12.15）

响应变量为正向类的概率是0.001，网络预测11=0。

12.4.3　训练一个多层感知机分类手写数字

在上一章中，我们使用了一个SVM来分类MNIST数据集中的手写数字。在本节内容中，我们将使用一个ANN来对这些图片进行分类，如代码12.3所示。

代码12.3

# In[1]:
from sklearn.datasets import load_digits
from sklearn.model_selection import cross_val_score
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.neural_network.multilayer_perceptron import
  MLPClassifier

if __name__ == '__main__':
    digits = load_digits()
    X = digits.data
    y = digits.target
    pipeline = Pipeline([
        ('ss', StandardScaler()),
        ('mlp', MLPClassifier(hidden_layer_sizes=(150, 100),
          alpha=0.1, max_iter=300, random_state=20))
    ])
    print(cross_val_score(pipeline, X, y, n_jobs=-1))

# Out[1]:
[ 0.94850498  0.94991653  0.90771812]

首先我们使用load_digits便捷函数来加载MNIST数据集，将在交叉验证期间生成额外的进程，这需要代码从一个main保护代码块中开始执行。对特征进行缩放对ANN来说非常重要，同时这样将保证一些学习算法更快的收敛。接着，我们在拟合一个MLPClassifier类之前，创建一个Pipeline对数据进行缩放。网络包含一个输出层，一个包含150个单元的隐层，第二个隐层包含100个单元以及一个输出层。我们也增加了正则化超参数alpha，同时将迭代最大次数从默认的200增加到300。最后，我们打印出三重交叉验证的准确率。准确率均值和支持向量分类器的准确率相差不多。增加更多的隐单元或者隐层，另外使用网格搜索来微调超参数可以进一步提升准确率。

12.5　小结

在本章中，我们介绍了ANN模型，它可以通过组合人工神经元表示复杂函数用于分类和回归。我们特别讨论了被称为前馈神经网络的有向无循环人工神经网络图。多层感知机是一种前馈神经网络，其每一层都和下一层全连接。一个包含一个隐层和有限数量隐单元的MLP是一种通用的函数逼近器。它可以表示任何连续函数，尽管它并不一定能自动学习来逼近权重值。我们描述了一个网络的隐层如何表示潜在变量，以及网络的权重如何能使用向后传播算法被学习。最后，我们使用了scikit-learn类库的多层感知机实现来逼近XOR函数以及分类手写数字。

本文摘自《scikit-learn机器学习（第2版）》

 

本书通过14章内容，详细地介绍了一系列机器学习模型和scikit-learn的使用技巧。本书从机器学习的基础理论讲起，涵盖了简单线性回归、K-近邻算法、特征提取、多元线性回归、逻辑回归、朴素贝叶斯、非线性分类、决策树回归、随机森林、感知机、支持向量机、人工神经网络、K-均值算法、主成分分析等重要话题。

本书适合机器学习领域的工程师学习，也适合想要了解scikit-learn的数据科学家阅读。通过阅读本书，读者将有效提升自己在机器学习模型的构建和评估方面的能力，并能够高效地解决机器学习难题。