超混沌Lorenz系统图像加密(MATLAB)
基于超混沌Lorenz系统的图像加密方案(MATLAB)
本研究提出一种基于Lorenz超混沌系统的图像加密方案。首先,生成Lorenz超混沌系统的初始值参数,并迭代生成密钥流。为改变原图像像素点的位置和灰度值大小,首先对图像进行加取模扩散以实现图像信息的第一次隐藏。其次,把二维图像的像素矩阵变成一维向量后,对一维向量进行无重复置乱再次隐藏图像的原始信息。然后,执行有限域扩散算法实现图像信息的第三次隐藏。为了实现明文像素点的信息扩散到整个密文图像中,加取模扩散算法需要循环两次。最后可以得到最终的密文图像。实验结果证明本研究所提出的图像加密方案是有效的,而且具有较强的抗攻击性以及密钥敏感性。
Lorenz超混沌系统定义
超混沌Lorenz系统是比较经典的混沌系统。它是Lorenz混沌系统的一种演变。主要定义如下:
dx/dt = a(y-x) + w
dy/dt = cx-y-xz
dz/dt = xy-bz
dw/dt = -yz + rw
当a = 10, b = 8/3, c = 28 且-1.52<= r <= -0.06时,系统处于超混沌状态,当r = -1时,上面公式的四个李雅普诺夫指数依次为:0.3381,0.1586,0和-15.1752,其中有两个正的李雅普诺夫指数。
龙格库塔法离散化Lorenz超混沌系统的公式
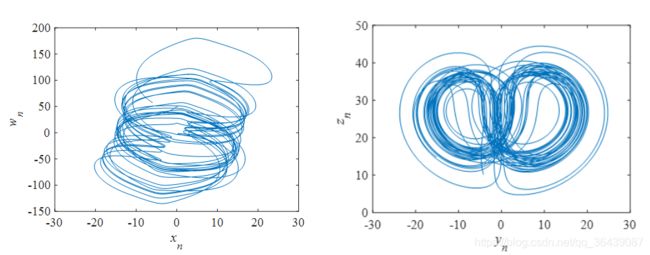
利用龙格库塔法离散化的Lorenz的公式所画出来的相图
利用上面公式在MATLAB软件上画出来的超混沌Lorenz系统相图如下图所示。其中步长h=0.002,总的状态点个数n=20000,对应的 Lorenz超混沌系统初始值取值范围为:x0:(-40,40) y0:(-40,40) z0:(1,81) w0:(-250,250)
%超混沌Lorenz相图
clear;clc
h = 0.002;%步长
n = 20000;%总的状态点数
t = 800;%过渡态的点数
a = 10;b = 8/3; c = 28; r = -1;%超混沌Lorenz系统的参数
x0 = 1.1; y0 = 2.2; z0 = 3.3; w0 =4.4;%初始值
xn = zeros(1,n);yn = zeros(1,n);zn = zeros(1,n);wn = zeros(1,n);
for i = 1:n + t
K11 = a * (y0 - x0) + w0;
K12 = a * (y0 - (x0 + K11 * h/2)) + w0;
K13 = a * (y0 - (x0 + K12 * h/2)) + w0;
K14 = a * (y0 - (x0 + K13 * h)) + w0;
x1 = x0 + (K11 + 2 * K12 + 2 * K13 +K14) * h/6;
K21 = c * x1 - y0 - x1 * z0;
K22 = c * x1 - (y0 + K21 * h/2) - x1 * z0;
K23 = c * x1 - (y0 + K22 * h/2) - x1 * z0;
K24 = c * x1 - (y0 +K23 * h) - x1 * z0;
y1 = y0 + (K21 + 2 * K22 + 2 * K23 + K24) * h/6;
K31 = x1 * y1 - b * z0;
K32 = x1 * y1 - b * (z0 + K31 * h/2);
K33 = x1 * y1 - b * (z0 + K32 * h/2);
K34 = x1 * y1 - b * (z0 + K33 * h);
z1 = z0 + (K31 + 2 * K32 + 2 * K33 +K34) * h/6;
K41 = -y1 * z1 + r * w0;
K42 = -y1 * z1 + r * (w0 + K41 * h/2);
K43 = -y1 * z1 + r * (w0 + K42 * h/2);
K44 = -y1 * z1 + r * (w0 + K43 * h);
w1 = w0 + (K41 + 2 * K42 + 2 * K43 + K44) * h/6;
x0 = x1;
y0 = y1;
z0 = z1;
w0 = w1;
if i > t
xn(i - t) = x1;
yn(i - t) = y1;
zn(i - t) = z1;
wn(i - t) = w1;
end
end
figure(1); plot(xn,yn);
xlabel('x_n','FontName','Times New Roman','FontSize',16,'FontAngle','Italic');
ylabel('y_n','FontName','Times New Roman','FontSize',16,'FontAngle','Italic');
set(gca,'FontName','Times New Roman','FontSize',16);
figure(2); plot(xn,zn);
xlabel('x_n','FontName','Times New Roman','FontSize',16,'FontAngle','Italic');
ylabel('z_n','FontName','Times New Roman','FontSize',16,'FontAngle','Italic');
set(gca,'FontName','Times New Roman','FontSize',16);
figure(3); plot(xn,wn);
xlabel('x_n','FontName','Times New Roman','FontSize',16,'FontAngle','Italic');
ylabel('w_n','FontName','Times New Roman','FontSize',16,'FontAngle','Italic');
set(gca,'FontName','Times New Roman','FontSize',16);
figure(4); plot(yn,zn);
xlabel('y_n','FontName','Times New Roman','FontSize',16,'FontAngle','Italic');
ylabel('z_n','FontName','Times New Roman','FontSize',16,'FontAngle','Italic');
set(gca,'FontName','Times New Roman','FontSize',16);
figure(5); plot(yn,wn);
xlabel('y_n','FontName','Times New Roman','FontSize',16,'FontAngle','Italic');
ylabel('w_n','FontName','Times New Roman','FontSize',16,'FontAngle','Italic');
set(gca,'FontName','Times New Roman','FontSize',16);
figure(6); plot(zn,wn);
xlabel('z_n','FontName','Times New Roman','FontSize',16,'FontAngle','Italic');
ylabel('w_n','FontName','Times New Roman','FontSize',16,'FontAngle','Italic');
set(gca,'FontName','Times New Roman','FontSize',16);
无重复置乱
基于有限域GF(257)的扩散
在图像加密系统中,扩散处理是在不改变像素点位置的条件下,将任一明文像素点的信息隐藏在尽可能多的密文像素点中。而有限域(Finite Field)亦称为伽罗瓦域Galois Fields,是仅含有有限个元素的域,它是伽罗瓦(Galois,E.)于18世纪30年代研究代数方程根式求解问题时引出的。有限域在编码理论和密码学等各方面有着广泛的应用。
在密码学中,有限域GF§是一个很重要的域,其中p为素数。它是整数的有限集合,并且使用模运算来执行基本的数学运算。本研究使用有限域GF(257)={0,1,…,256},其中257为素数。GF(257)的算术运算以257为模,这个集合一共包含257个元素。在乘法运算中,为了减少元素0带来的信息损失,可以剔除元素0,然后使用剩下的256个元素来进行算术运算,这是元素的个数为256,正好对应图像像素点灰度值的取值范围。
有限域公式:

Matlab加密函数如下
% 典型混沌数字图像密码系统加密函数TpEncrypt
% 置乱算法采用将二维图像展开成一维向量后的无重复置乱算法
% 扩散算法采用基于GF(257)域乘法运算的扩散算法
% 输入明文图像 P和秘钥K(向量形式),输出密文图像C
function C = TpEncrypt(P,K)
[M,N] = size(P);P = double(P);n = 3 * M * N;s = zeros(1,n);%混沌序列,伪随机数组,为浮点数
h = 0.002; %步长
t = 800; %过渡态的点数
a = 10;b = 8/3; c = 28; r = -1;%超混沌Lorenz系统的参数
x0 = K(1); y0 = K(2); z0 = K(3); w0 = K(4);%初始值
%超混沌Lorenz系统,生成伪随机数
for i = 1:n + t
K11 = a * (y0 - x0) + w0;
K12 = a * (y0 - (x0 + K11 * h/2)) + w0;
K13 = a * (y0 - (x0 + K12 * h/2)) + w0;
K14 = a * (y0 - (x0 + K13 * h)) + w0;
x1 = x0 + (K11 + 2 * K12 + 2 * K13 +K14) * h/6;
K21 = c * x1 - y0 - x1 * z0;
K22 = c * x1 - (y0 + K21 * h/2) - x1 * z0;
K23 = c * x1 - (y0 + K22 * h/2) - x1 * z0;
K24 = c * x1 - (y0 +K23 * h) - x1 * z0;
y1 = y0 + (K21 + 2 * K22 + 2 * K23 + K24) * h/6;
K31 = x1 * y1 - b * z0;
K32 = x1 * y1 - b * (z0 + K31 * h/2);
K33 = x1 * y1 - b * (z0 + K32 * h/2);
K34 = x1 * y1 - b * (z0 + K33 * h);
z1 = z0 + (K31 + 2 * K32 + 2 * K33 +K34) * h/6;
K41 = -y1 * z1 + r * w0;
K42 = -y1 * z1 + r * (w0 + K41 * h/2);
K43 = -y1 * z1 + r * (w0 + K42 * h/2);
K44 = -y1 * z1 + r * (w0 + K43 * h);
w1 = w0 + (K41 + 2 * K42 + 2 * K43 + K44) * h/6;
x0 = x1;%迭代
y0 = y1;
z0 = z1;
w0 = w1;
if i > t
s(i - t) = x1;
if mod((i - t),3000) == 0%每3000次迭代后对混沌状态x0进行小的扰动
x0 = x0 + h * sin(y0);
end
end
end
%Smod1和Smod2保存正向算法与逆向算法的伪随机数向量,此混沌序列用于加取模扩散算法中
Smod = mod(floor(s * pow2(16)),256);
Smod1 = Smod(1:M * N);Smod2 = Smod(M * N + 1:2 * M * N);Bmod = zeros(M,N);Cmod = zeros(M,N);
% 行和列一起置乱
% 得到置乱用的伪随机序列 保存在X中
X = mod(floor((s(1:M * N) + 100) * 10 ^ 10),M * N) + 1;
[~, idx] = unique(X);L = length(idx);X1 =zeros(1,M * N);
X1(1:length(idx)) = X(sort(idx));
X1(length(idx) + 1:M * N) = setdiff(1:M*N,X1);X = X1;%不重复
%生成扩散用的伪随机序列,保存在S1和S2中
%构建乘法运算表
TBL = GF257Table();
S = mod(floor(s(M * N + 1:3 * M * N) * pow2(16)),256);
S1 = S(1:M * N);S2 = S(M * N + 1:2 * M * N);B = zeros(M,N);C = zeros(M,N);
%加取模扩散算法实现
Amod = P(:);Bmod0 = 0;Bmod(1) = mod(Bmod0 + Smod1(1) + Amod(1),256);
for i = 2:M * N
Bmod(i) = mod(Bmod(i - 1) + Smod1(i) + Amod(i),256);
end
Cmod0 = 0;Cmod(M * N) = mod(Cmod0 + Smod2(M * N) + Bmod(M * N),256);
for i = M * N - 1:-1:1
Cmod(i) = mod(Cmod(i + 1) + Smod2(i) + Bmod(i),256);
end
%循环第二次加取模扩散算法
Amod1 = Cmod;Bmod1 = zeros(M,N);Cmod1 = zeros(M,N);
Bmod01 = 0;Bmod1(1) = mod(Bmod01 + Smod1(1) + Amod1(1),256);
for i = 2:M * N
Bmod1(i) = mod(Bmod1(i - 1) + Smod1(i) + Amod1(i),256);
end
Cmod01 = 0;Cmod1(M * N) = mod(Cmod01 + Smod2(M * N) + Bmod1(M * N),256);
for i = M * N - 1:-1:1
Cmod1(i) = mod(Cmod1(i + 1) + Smod2(i) + Bmod1(i),256);
end
% 置乱算法采用将二维图像展开成一维向量后的无重复置乱算法
A = Cmod1;
for i = 1:floor(M * N/2)
t = A(X(i));
A(X(i)) = A(X(M * N - i + 1));
A(X(M * N - i + 1)) = t;
end
% 扩散算法采用基于GF(257)域乘法和除法运算的扩散算法
B0 = 0;B(1) = LookUpGF257(B0,S1(1),A(1),TBL);%LookUpGF257为乘法运算
for i = 2:M * N
B(i) = LookUpGF257(B(i -1),S1(i),A(i),TBL);
end
C0 = 0;C(M * N) = LookUpGF257(C0,S2(M * N),B(M * N),TBL);
for i = M * N - 1:-1:1
C(i) = LookUpGF257(C(i + 1),S2(i),B(i),TBL);
end
C = reshape(C,M,N);C = uint8(C);
end
构建乘法运算表TBL = GF257Table(),其函数如下:
%GF(257)域的乘法运算表
function T = GF257Table()
T = mod(transpose(0:256)*(0:256),257);
end
扩散算法采用基于GF(257)域的乘法运算
% 基于GF(257)域的乘法运算函数 x0 * x1 * x2
function y = LookUpGF257(x0,x1,x2,TBL)
y = TBL(TBL(x0 + 2,x1 + 2) + 1,x2 + 2) - 1;
end
Matlab解密函数如下
% 典型混沌数字图像密码系统解密函数TpDecrypt
% 置乱算法采用将二维图像展开成一维向量后的无重复置乱算法
% 扩散算法采用基于GF(257)域乘法运算的扩散算法
% 输入密文图像C和秘钥K(向量形式),输出解密后的图像P
function P = TpDecrypt(C,K)
[M,N] = size(C);C = double(C);n = 3 * M * N;s = zeros(1,n);%混沌序列,伪随机数组,为浮点数
h = 0.002; %步长
t = 800; %过渡态的点数
a = 10;b = 8/3; c = 28; r = -1;%超混沌Lorenz系统的参数
x0 = K(1); y0 = K(2); z0 = K(3); w0 = K(4);%初始值
%超混沌Lorenz系统,生成伪随机数
for i = 1:n + t
K11 = a * (y0 - x0) + w0;
K12 = a * (y0 - (x0 + K11 * h/2)) + w0;
K13 = a * (y0 - (x0 + K12 * h/2)) + w0;
K14 = a * (y0 - (x0 + K13 * h)) + w0;
x1 = x0 + (K11 + 2 * K12 + 2 * K13 +K14) * h/6;
K21 = c * x1 - y0 - x1 * z0;
K22 = c * x1 - (y0 + K21 * h/2) - x1 * z0;
K23 = c * x1 - (y0 + K22 * h/2) - x1 * z0;
K24 = c * x1 - (y0 +K23 * h) - x1 * z0;
y1 = y0 + (K21 + 2 * K22 + 2 * K23 + K24) * h/6;
K31 = x1 * y1 - b * z0;
K32 = x1 * y1 - b * (z0 + K31 * h/2);
K33 = x1 * y1 - b * (z0 + K32 * h/2);
K34 = x1 * y1 - b * (z0 + K33 * h);
z1 = z0 + (K31 + 2 * K32 + 2 * K33 +K34) * h/6;
K41 = -y1 * z1 + r * w0;
K42 = -y1 * z1 + r * (w0 + K41 * h/2);
K43 = -y1 * z1 + r * (w0 + K42 * h/2);
K44 = -y1 * z1 + r * (w0 + K43 * h);
w1 = w0 + (K41 + 2 * K42 + 2 * K43 + K44) * h/6;
x0 = x1;%迭代
y0 = y1;
z0 = z1;
w0 = w1;
if i > t
s(i - t) = x1;
if mod((i - t),3000) == 0%每3000次迭代后对混沌状态x0进行小的扰动
x0 = x0 + h * sin(y0);
end
end
end
%Smod1和Smod2保存正向算法与逆向算法的伪随机数向量,此混沌序列用于加取模扩散算法中
Smod = mod(floor(s * pow2(16)),256);
Smod1 = Smod(1:M * N);Smod2 = Smod(M * N + 1:2 * M * N);Bmod = zeros(M,N);Cmod = zeros(M,N);
% 行和列一起置乱
% 得到置乱用的伪随机序列 保存在X中
X = mod(floor((s(1:M * N) + 100) * 10 ^ 10),M * N) + 1;
[~, idx] = unique(X);L = length(idx);X1 =zeros(1,M * N);
X1(1:length(idx)) = X(sort(idx));
X1(length(idx) + 1:M * N) = setdiff(1:M*N,X1);X = X1;%不重复
%生成扩散用的伪随机序列,保存在S1和S2中
%构建乘法运算表TBL1和除法运算表TBL2
[TBL1,TBL2] = GF257TableEx();
S = mod(floor(s(M * N + 1:3 * M * N) * pow2(16)),256);
S1 = S(1:M * N);S2 = S(M * N + 1:2 * M * N);
%解密是逆过程
A = C(:);D = zeros(1,M * N);E = zeros(1,M * N);
% 扩散算法采用基于GF(257)域乘法和除法运算的扩散算法
A0 = 0;D(M * N) = LookUpGF257Ex2(A(M * N),A0,S2(M * N),TBL1,TBL2);
for i = M * N - 1:-1:1
D(i) = LookUpGF257Ex2(A(i),A(i + 1),S2(i),TBL1,TBL2);
end
E0 = 0;E(1) = LookUpGF257Ex2(D(1),E0,S1(1),TBL1,TBL2);
for i = 2:M * N
E(i) = LookUpGF257Ex2(D(i),D(i - 1),S1(i),TBL1,TBL2);
end
% 置乱算法采用将二维图像展开成一维向量后的无重复置乱算法
for i = 1:floor(M * N/2)
t = E(X(i));
E(X(i)) = E(X(M * N - i + 1));
E(X(M * N - i + 1)) = t;
end
%循环第二次加取模逆向扩散算法
Cmod1 = E;Dmod1 = zeros(M,N);Emod1 = zeros(M,N);
Dmod01 = 0;Dmod1(M * N) = mod(256 * 2 + Cmod1(M * N) - Dmod01 - Smod2(M * N),256);
for i = M * N - 1:-1:1
Dmod1(i) = mod(256 * 2 + Cmod1(i) - Cmod1(i + 1) - Smod2(i),256);
end
Emod01 = 0;Emod1(1) = mod(256 * 2 + Dmod1(1) - Emod01 -Smod1(1),256);
for i = 2:M * N
Emod1(i) = mod(256 * 2 + Dmod1(i) - Dmod1(i -1) - Smod1(i),256);
end
%加取模扩散算法实现
Cmod = Emod1;Dmod = zeros(M,N);Emod = zeros(M,N);
Dmod0 = 0;Dmod(M * N) = mod(256 * 2 + Cmod(M * N) - Dmod0 - Smod2(M * N),256);
for i = M * N - 1:-1:1
Dmod(i) = mod(256 * 2 + Cmod(i) - Cmod(i + 1) - Smod2(i),256);
end
Emod0 = 0;Emod(1) = mod(256 * 2 + Dmod(1) - Emod0 -Smod1(1),256);
for i = 2:M * N
Emod(i) = mod(256 * 2 + Dmod(i) - Dmod(i -1) - Smod1(i),256);
end
%将扩散置乱后的一维数据图像矩阵转换为二维矩阵形式
P = reshape(Emod,M,N);P = uint8(P);
end
解密需要构建乘法运算表TBL1和除法运算表TBL2,MATLAB代码如下:
%GF(257)域的乘法和除法运算表
function [T1,T2] = GF257TableEx()
T1 = mod(transpose(0:256)*(0:256),257);%乘法运算表
T2 = zeros(257,257);%除法运算表
T2(:,1) = transpose(0:256);
for j = 1:256
for k = 1:256
T2(mod(j * k,257) + 1,j + 1) = k;
end
end
end
扩散算法采用基于GF(257)域乘法和除法运算的扩散算法
% 基于GF(257)域的除法运算函数 x0 / x1 / x2
% 需要构建除法表
function y = LookUpGF257Ex2(x0,x1,x2,TBL1,TBL2)
t = TBL1(x1 + 2,x2 + 2) + 1;
y = TBL2(x0 + 2,t) -1;
end
论文题目:An image encryption scheme based on Lorenz Hyperchaotic System and RSA algorithm
论文地址:https://www.researchgate.net/publication/351054043_An_Image_Encryption_Scheme_Based_on_Lorenz_Hyperchaotic_System_and_RSA_Algorithm