42. 接雨水

42. 接雨水

42. 接雨水

核心思路

首先我们要明确本题的核心思路：逐个计算每个位置处的雨水量再加和，每个位置处的雨水量由它左侧柱子的最高值和右侧柱子的最高值中较小的那一个决定。我们先实现一个暴力的方法，再来逐步优化。

暴力方法

暴力方法足够暴力，我们从左到右遍历数组，并在每个位置求其左右的最大值，加上它们中较小的那一个：

class Solution {
public:
    int trap(vector<int>& height) {
        int ans = 0;
        for (int i=1; i<height.size(); ++i) {
            auto max_left_ite = max_element(height.begin(), height.begin()+i+1);
            auto max_right_ite = max_element(height.begin()+i, height.end());
            int curr = min(*max_left_ite, *max_right_ite);
            ans += (curr - height[i]);
        }
        return ans;
    }
};

暴力方法时间复杂度为 $O(n^2)$ ，空间复杂度为 $O(1)$ 。

动态规划（记忆化）

很明显，暴力做法中每次都计算当前位置左右全部的最大值是有着大量的冗余计算的，我们可以维护一个 dp 数组：

dp数组含义

$dp[i][0],dp[i][1]$ 分别表示位置 $i$ 左侧和右侧的最大值。

状态转移公式

$dp[i][0]=max(dp[i-1][0],height[i])$ ，$dp[i][1]=max(dp[i+1][1],height[i])$

非常容易理解，就是每次看一下当前位置的值，是否比之前/之后的都大，更新上即可。

遍历顺序

我们要从前到后，从后到前遍历两次，分别去更更新左侧的最大值和右侧的最大值。

dp数组初始化

对于从前到后，更新左侧的遍历，我们要初始化 $dp[0][0]$ 为 $height[0]$ ；对于从前到后，更新左侧的遍历，我们要初始化 $dp[n-1][1]$ 为 $height[n-1]$ 。

明确了以上几点之后，代码就很好写了：

class Solution {
public:
    int trap(vector<int>& height) {
        int n = height.size();
        vector<vector<int>> dp(n, vector<int> (2));
        dp[0][0] = height[0], dp[n-1][1] = height[n-1];
        for (int i=1; i<n; ++i) dp[i][0] = max(height[i], dp[i-1][0]);
        for (int i=n-2; i>0; --i) dp[i][1] = max(height[i], dp[i+1][1]);

        int ans = 0;
        for (int i=1; i<n; ++i) {
            int curr = min(dp[i][0], dp[i][1]);
            ans += (curr - height[i]);
        }
        return ans;
    }
};

动态规划方法暴力方法时间复杂度为 $O(n)$ ，空间复杂度为 $O(n)$ 。

双指针

双指针的方法笔者认为还是比较巧妙的，我们再回头看一下我们的思路：

逐个计算每个位置处的雨水量再加和，每个位置处的雨水量由它左侧柱子的最高值和右侧柱子的最高值中较小的那一个决定。我们先实现一个暴力的方法，再来逐步优化。

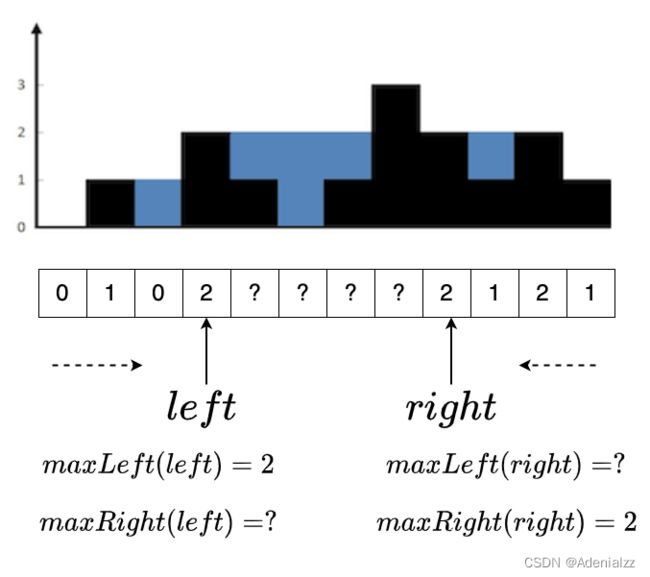
我们分别设置两个指针从左到右/从右到左来遍历数组，在遍历过程中分别更新左指针左侧的最大值和右指针右侧的最大值。

需要注意，左指针左侧的最大值是已知的，但是右侧的最大值左指针目前是不知道的，因为我们是从左右向中间遍历，左右指针中间的元素还未知，不知道会不会有比右指针右侧的值更大的。同理，右指针右侧的最大值是已知的，左侧的最大值未知。

只知道单侧的最大值，但是我们需要的是左右两侧最大值的较小者，这样我们怎么计算每个位置的雨水量呢？

实际上，我们可以每一步比对一下当前左右指针已经能确定一侧的最大值，然后去更新较小者的雨水量。

比如我们比对当前左指针左侧的最大值和右指针右侧的最大值，发现左指针左侧的最大值是较小的，我们其实就可以大胆地去按照左指针左侧的最大值来计算左指针处的雨水量了，因为中间的这一块未知区域，只有可能让左指针右侧的最大值更大，但是到底有多大都无所谓了，因为我们要的是两侧最大值的较小者，而我们现在已经能确定左指针左侧的最大值较小了，直接按照其计算当前指针处的雨水量即可。

class Solution {
public:
    int trap(vector<int>& height) {
        int n = height.size();
        int left = 0, right = n - 1;
        int ans = 0;
        int leftMax = height[0], rightMax = height[n-1];
        while (left <= right) {
            if (leftMax < rightMax) {
                leftMax = max(leftMax, height[left]);
                ans += leftMax - height[left++];
            }
            else {
                rightMax = max(rightMax, height[right]);
                ans += rightMax - height[right--];
            }
        }
        return ans;
    }
};

动态规划方法暴力方法时间复杂度为 $O(n)$ ，空间复杂度为 $O(1)$ 。注意这里的时间复杂度虽然与动态规划方法同为 $O(n)$ ，但是这里我们只用了一次遍历。

单调栈

TODO

class Solution {
public:
    int trap(vector<int>& height) {
        int ans = 0;
        stack<int> stk;
        int n = height.size();
        for (int i = 0; i < n; ++i) {
            while (!stk.empty() && height[i] > height[stk.top()]) {
                int top = stk.top();
                stk.pop();
                if (stk.empty()) {
                    break;
                }
                int left = stk.top();
                int currWidth = i - left - 1;
                int currHeight = min(height[left], height[i]) - height[top];
                ans += currWidth * currHeight;
            }
            stk.push(i);
        }
        return ans;
    }
};