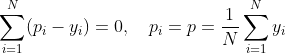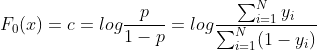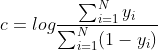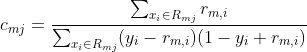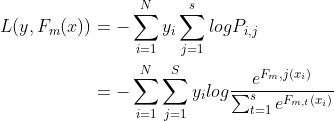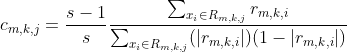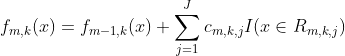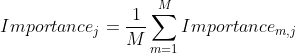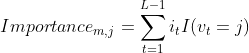3. 梯度提升决策树(GBDT)详解
一、提升树
以决策树为基函数的提升方法称为提升树。其中,分类问题采用二叉分类树,回归问题采用二叉回归树。sklearn中的提升树采用的是CART树。模型可以表示为决策树的加法模型:
其中,![]() 表示决策树,
表示决策树,![]() 为决策树的参数,
为决策树的参数,![]() 为树的个数。
为树的个数。
提升树算法采用前向分步算法。首先,初始确定初始提升树为![]() 。第
。第![]() 步的模型是
步的模型是![]()
其中,![]() 为当前模型,通过经验风险极小化确定下一棵决策树的参数
为当前模型,通过经验风险极小化确定下一棵决策树的参数![]()
由于树的线性组合能很好地拟合训练数据,即使数据中的输入与输出关系很复杂也是如此,所以提升树是一个高功能的学习算法。
不同提升树算法的区别在于所采用的损失函数不同。例如,分类树采用指数损失函数;回归树采用平方误差损失函数;一般决策树采用一般损失函数。
1. 回归问题提升树
在之前的文章中已经介绍过二叉回归树,在这里不在进行赘述。对于回归问题,提升树采用平方误差损失函数,即
![]()
带入第![]() 步得到的提升树模型,得到
步得到的提升树模型,得到
其中,![]() 为训练数据真实值与当前模型取值的差,即拟合数据的残差。要是上述的损失函数最小,只需训练的模型更好地拟合当前模型的残差即可。
为训练数据真实值与当前模型取值的差,即拟合数据的残差。要是上述的损失函数最小,只需训练的模型更好地拟合当前模型的残差即可。
回归问题的提升树算法可描述如下:
输入:训练数据集D
输出:提升树![]()
训练过程:
① 初始化![]()
② 对![]()
(a)计算残差
![]()
(b)拟合残差![]() ,学习一个二叉回归树,得到
,学习一个二叉回归树,得到![]()
(c)更新![]()
③ 得到回归问题提升树
2. 分类问题提升树
对于二分类问题,只需要将AdaBoost算法中的基学习器限制为二类分类树(只有一个根结点和两个叶子结点,高度为2的二叉树),基分类器的权重全部置为1即可。训练过程中用指数损失函数来调整样本数据的权重,从而让每个基分类器学习到不同的内容。
二、梯度下降
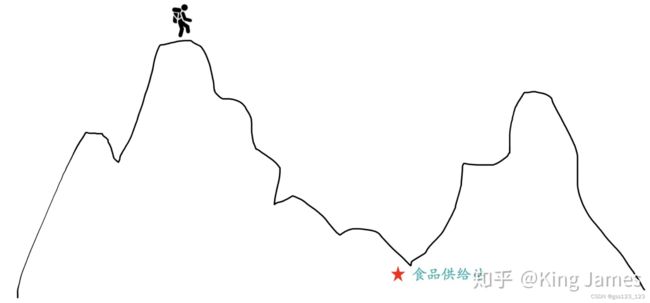
首先介绍梯度下降法的整体思想。假设你现在站在某个山峰的顶峰,在天黑前要到达山底,在不考虑安全性的基础上,如何下山最快?
最快的方法是:以当前所在的位置为基准点,按照该点最陡峭的方向向山底前进。走一段距离后,在重新以当前点为基准点,重复上述操作,知道到底山底(最低点)。在这个过程中,需要不停地去重新定位最陡峭的方向,才不会限于局部最优。
在下山过程中会面临两个问题:
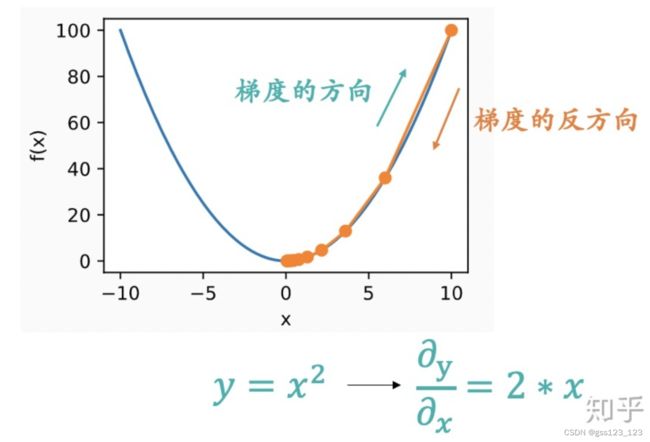
- 如何测量山峰的“陡峭”程度;这就是梯度。梯度是一个向量,梯度的方向是函数在指定点上升最快的方向,那么梯度的反方向自然就是下降最快的方向。计算方式是函数求偏导。
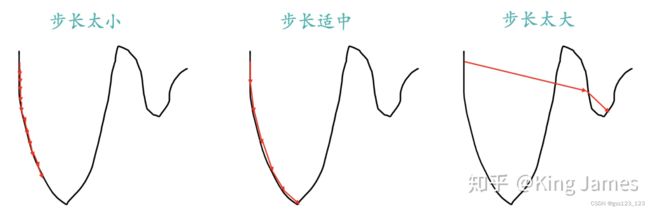
- 每一步需要走多远;走太长距离,可能会错过最佳路线;最太短,下降速度会比较慢。这是步长。
当前位置的梯度表示为![]() ,取步长
,取步长![]() ,则下一步所在的位置如下:
,则下一步所在的位置如下:
总结:梯度下降用来求某个函数取最小值时,自变量对应的取值。
1. 机器学习任务中的梯度下降
在机器学习任务中,梯度下降一般运用在通过损失函数![]() 最小化求解模型参数
最小化求解模型参数![]() 中。使用梯度下降算法求解最优模型参数
中。使用梯度下降算法求解最优模型参数![]() 的过程如下:
的过程如下:
(2)用步长![]() 乘以损失函数的梯度,得到当前位置下降的距离,即:
乘以损失函数的梯度,得到当前位置下降的距离,即:![]() ;
;
(3)判断梯度下降的距离是否小于阈值![]() ,如果小于,则算法终止,当前的
,如果小于,则算法终止,当前的![]() 即为求得的最优参数;否则进入步骤(4);
即为求得的最优参数;否则进入步骤(4);
从泰勒公式的角度理解梯度下降:
(1)首先,给出迭代公式:![]()
(2)将![]() 在
在![]() 处展开:
处展开:
![]()
移项可得:
![]()
其中,![]() 和
和![]() 均为向量,
均为向量,![]() 表示二者点乘,当二者方向相同,即夹角为0时,点乘的值最大。这个点乘代表了从
表示二者点乘,当二者方向相同,即夹角为0时,点乘的值最大。这个点乘代表了从![]() 到
到![]() 函数值的上升量。
函数值的上升量。![]() 为
为![]() 在
在![]() 处的梯度,这也说明了当
处的梯度,这也说明了当![]() 与梯度方向相同时,函数值上升最快;反之,如果
与梯度方向相同时,函数值上升最快;反之,如果![]() 与负梯度方向相同(与梯度方向相反时),函数梯度下降的最快。所以
与负梯度方向相同(与梯度方向相反时),函数梯度下降的最快。所以![]() 可以取
可以取![]() ,此时,
,此时,![]() 与负梯度方向相同,函数值下降最快,这正式所需要的,因为目标是最小化损失函数,损失函数值下降的越快越好。于是,参数的迭代公式如下:
与负梯度方向相同,函数值下降最快,这正式所需要的,因为目标是最小化损失函数,损失函数值下降的越快越好。于是,参数的迭代公式如下:
![]()
三、梯度提升树(GBDT)
在提升树算法中,对于损失函数采用平方误差或者指数损失时,每一步的优化是比较简单的,但是对于一般损失函数,则很难进行。针对这一问题,Friedman提出了梯度提升树算法,利用最速下降的近似方法,将当前模型的损失函数的负梯度作为提升树算法中残差的近似值,即每一步的基学习器(CART回归树)拟合损失函数的负梯度。
1. Boosting算法中的梯度下降
梯度提升算法有梯度下降和Boosting两部分组成。常规的梯度下降是在参数空间进行地,目的是得到最优的模型参数。这里的梯度下降是在函数空间进行,目的是得到最优的模型。
提升树第m步的模型可以表示为:
![]()
其中,![]() 是已知的,所以求出
是已知的,所以求出![]() 也就求得
也就求得![]() 。此时,要优化的损失函数如下:
。此时,要优化的损失函数如下:
将![]() 在
在![]() 处进行一阶泰勒展开:
处进行一阶泰勒展开:
可以发现公式中的梯度变量变为模型(函数),所以说是在函数空间进行的梯度下降。在常规的梯度下降中,为了使损失函数下降最快,到这一步后是直接取负梯度乘上步长来更新参数;但是在Boosting算法中,我们要更新的是模型,而不是参数,所以只能让模型来拟合负梯度,即在第m步中,![]() 的求解公式如下:
的求解公式如下:
求出![]() 就可以求出
就可以求出![]() 。
。
2. GBDT回归树
处理回归问题时,GBDT一般使用平方误差损失函数,损失函数的负梯度即为残差。平方误差损失函数如下:
对![]() 求梯度得
求梯度得
GBDT回归树的训练流程如下:
输入:训练数据集![]() ,损失函数
,损失函数![]() (一般是平方误差损失函数),学习率
(一般是平方误差损失函数),学习率![]() (梯度下降算法中的步长);
(梯度下降算法中的步长);
输出:回归树![]() 。
。
训练过程:
① 初始化
在损失函数是平方误差损失函数时,取标签的平均值。
② 对![]()
(a)对![]() ,计算
,计算
当损失函数为平方误差损失函数时,负梯度等于残差。
(b)对![]() 拟合一个CART回归树,得到第
拟合一个CART回归树,得到第![]() 棵树的叶结点区域
棵树的叶结点区域![]() 。
。
(c)对![]() ,计算
,计算
利用线性搜索估计叶结点区域的值,使得损失函数极小化。损失函数为平方误差损失函数时,![]() 等于第
等于第![]() 个叶结点区域的全部样本标签的平均值。
个叶结点区域的全部样本标签的平均值。
③ 得到回归树
在训练过程中,如果选择了合适的步长![]() ,损失函数的梯度是逐渐递减的,当损失函数的梯度为0时,达到极值点,此时,残差也必然接近0,损失函数获得最小值。因此,迭代生成CART树的过程本质是梯度减小的过程,是一个二次函数优化的过程。
,损失函数的梯度是逐渐递减的,当损失函数的梯度为0时,达到极值点,此时,残差也必然接近0,损失函数获得最小值。因此,迭代生成CART树的过程本质是梯度减小的过程,是一个二次函数优化的过程。
3. GBDT分类树
对于分类问题,GBDT的基学习器也是CART回归树。与回归问题的区别在于使用的损失函数不同。分类问题通常使用交叉熵作为损失函数,交叉熵损失函数形式如下:
其中,![]() 表示样本数量,
表示样本数量,![]() 表示类别数量,
表示类别数量,![]() 表示第
表示第![]() 个样本属于第
个样本属于第![]() 个类别,
个类别,![]() 表示将
表示将![]() 个样本预测为第
个样本预测为第![]() 个类别的概率。
个类别的概率。
CART回归树的叶子结点值是一个实数,对于回归问题,由损失函数最优化,可得叶子结点的取值为样本标签的均值。由于分类问题,样本标签是离散值,使用交叉熵损失函数,所以需要把预测的实数转换成概率。
(1)二分类问题
在二分类问题中(类别标签取值为0或者1),可以与逻辑回归一样,使用Sigmoid函数即可把实数值转变成概率形式,如下:
其倒数为:![]() 。
。
首先,求各叶结点的取值。
二分类问题中,使用的交叉熵损失函数,可写成如下形式:
假设,在生成CART树的过程中,第m轮的树为![]() ,样本被预测为正样本的概率可以用如下形式表示:
,样本被预测为正样本的概率可以用如下形式表示:
损失函数为:
由一阶泰勒展开式
![]()
其中,![]() 为各叶结点的取得的实数值。上述式子对
为各叶结点的取得的实数值。上述式子对![]() 求导:
求导:
由于,导数为0时,可以取得最优值,令上述导数为0,可求得:
以上,即为第![]() 生成的叶结点的取值。
生成的叶结点的取值。
下面,来求初始值![]() ,损失函数函数:
,损失函数函数:
其中,![]() 为常数,
为常数,![]() 对
对![]() 求导,并且令导数为0,此时,损失函数取得最优值,求得:
求导,并且令导数为0,此时,损失函数取得最优值,求得:
GBDT二分类树的训练流程如下:
输入:训练数据集![]() ,其中,
,其中,![]() ,损失函数
,损失函数![]() (一般是交叉熵损失函数),学习率
(一般是交叉熵损失函数),学习率![]() (梯度下降算法中的步长);
(梯度下降算法中的步长);
输出:二分类树![]() 。
。
训练过程:
① 初始化
② 对![]()
(a)对![]() ,计算
,计算
当损失函数时交叉熵时,负梯度等于残差。
(b)对![]() 拟合一个CART回归树,得到第
拟合一个CART回归树,得到第![]() 棵树的叶结点区域
棵树的叶结点区域![]() 。
。
(c)对![]() ,计算
,计算
利用线性搜索估计叶结点区域的值,使得损失函数极小化。损失函数为交叉熵损失函数时,
③ 得到二分类树
分类和回归中所使用的到回归树是一样的,传入属性值作为分裂待选结点,利用残差作为目标值,回归树regression_tree使用平方差函数作为信息增益函数。
(2)多分类问题
二分类可拓展至多分类,采用one vs rest的策略,假设有s个类别,则每轮需要训练s棵树,每一棵树用来判断是否属于其中的一个类别。其中,样本的类型标签,需要进行one-hot处理,生成s为列向量。第m轮,第k棵树(用来识别类别k),CART树为![]() ,利用softmax函数可以将
,利用softmax函数可以将![]() 转化为概率:
转化为概率:
![]()
使用交叉熵作为损失函数,得到如下损失函数表达式:
利用softmax函数性质,损失函数对m轮第q棵树求导,可得:
可以看出,GBDT的多分类仍然是残差的形式。
GBDT多分类树的训练流程如下:
输入:训练数据集![]() ,其中,
,其中,![]() ,损失函数
,损失函数![]() (一般是交叉熵损失函数),学习率
(一般是交叉熵损失函数),学习率![]() (梯度下降算法中的步长);
(梯度下降算法中的步长);
输出:s棵二分类树![]() 。
。
训练过程:
① 对样本的类别标签进行one-hot向量化,生成![]() 维类别向量,每行数据只含有0或1,即为二分类问题。
维类别向量,每行数据只含有0或1,即为二分类问题。
② 初始化![]() 棵树的初始值
棵树的初始值
③ 对![]()
(a)对![]() ,
,
(i)对![]() ,利用softmax函数,计算出第
,利用softmax函数,计算出第![]() 个样本属于第
个样本属于第![]() 个类别的概率:
个类别的概率:
![]()
(ii)对![]() ,计算负梯度,由上述描述可知,亦为样本的残差
,计算负梯度,由上述描述可知,亦为样本的残差
(b)对![]() ,拟合一棵CART回归树,得到第
,拟合一棵CART回归树,得到第![]() 轮,第
轮,第![]() 棵树的叶结点区域
棵树的叶结点区域![]() 。
。
(c)对![]() ,计算
,计算
利用线性搜索估计叶结点区域的值,使得损失函数极小化。损失函数为交叉熵损失函数时,
(d)更新
③ 得到s棵二分类树
![]()
四、GBDT特征重要度的计算
Friedman在GBM的论文中提出的方法: 特征![]() 的全局重要性,通过特征
的全局重要性,通过特征![]() 在单棵树中的重要度的均值来衡量,即
在单棵树中的重要度的均值来衡量,即
其中,![]() 表示特征
表示特征![]() 在第
在第![]() 轮训练的CART回归树中的重要度。
轮训练的CART回归树中的重要度。
其中,![]() 表示第
表示第![]() 棵树的内部结点,
棵树的内部结点,![]() 为树的叶结点数(由完全二叉树的性质,树的内部结点数=叶结点数-1),
为树的叶结点数(由完全二叉树的性质,树的内部结点数=叶结点数-1),![]() 表示,在结点
表示,在结点![]() 分裂后减小的平方误差损失,
分裂后减小的平方误差损失,![]() 表示当前结点分裂时使用的特征。
表示当前结点分裂时使用的特征。
五、优缺点
(1)GBDT算法优点
- 预测精度高
- 适合低维数据
- 能处理非线性数据
- 可以灵活处理各类型的数据,包括连续值和离散值
- 在相对少的调参时间情况下,预测的准确率也可以比较高(这是相对SVM来说的)
- 使用一些健壮的损失函数,对异常值的鲁棒性非常棒,比如Huber损失函数和Quantile损失函数
(2)GBDT算法缺点
- 由于弱学习器之间存在依赖关系,难以进行并行训练数据,不过可以通过自采用的SGBT来达到部分并行
- 数据维度较高时,会加大算法的计算复杂度
六、GBDT与AdaBoost的区别
- GBDT集成的对象必须是CART回归树,而AdaBoosting集成目标是弱分类器
- 两者迭代的方式也有区别,AdaBoosting利用上一轮错误率来更新下一轮分类器的权重、从而实现最终识别能力的提升;而GBDT使用梯度来实现模型的提升,算法中利用残差来拟合梯度,通过不断减小残差实现梯度的下降
附录
1. 机器学习之梯度提升决策树(GBDT)_谓之小一的博客-CSDN博客_梯度提升决策树
2. GBDT的原理、公式推导、Python实现、可视化和应用 - 知乎
3. 《统计学习方法 第二版》.李航
4. GBDT算法——理论与sklearn代码实现 - 知乎
5. Sklearn参数详解—GBDT - 百度文库
6. GBDT算法的特征重要度计算_yangxudong的博客-CSDN博客_gbdt特征重要性
7. 梯度提升决策树-GBDT
8. 通俗易懂讲解梯度下降法 - 知乎
9. 梯度下降(详解)_流年若逝的博客-CSDN博客_梯度下降
10. GBDT原理与实践-多分类篇_kingsam_的博客-CSDN博客_gbdt多分类
11. GBDT算法的优缺点_suv1234的博客-CSDN博客_gbdt优点
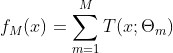
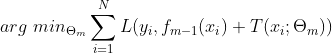
![\begin{aligned} L(y, f(x)) &= [y - f(x)]^2 \\&=[y - f_{m-1}(x) - T(x; \Theta _m)]^2 \\ & =[r - T(x;\Theta _m)]^2 \end{aligned}](http://img.e-com-net.com/image/info8/46691dcb72e7409894c04d087ad13040.gif)
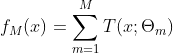
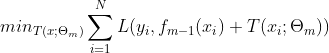
![T(x_i;\Theta _m) = argmin_{T \in \tau } \sum_{i=1}^{N} [ -\frac{\partial {L}'(y_i, f_{m-1}(x_i))}{\partial f_{m-1}(x_i)}- T(x_i; \Theta _m)]^2](http://img.e-com-net.com/image/info8/c2ab233077cf4306ac4e8fcac6fc22ab.gif)
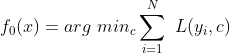
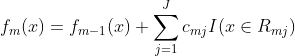
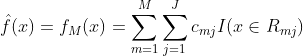
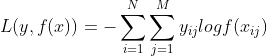
![L(y, f(x)) =- \sum_{i=1}^{N} [y_i logf(x_i) + (1-y_i)log(1-f(x_i))]](http://img.e-com-net.com/image/info8/b5d21281c56b412ca62032693a7cbc9a.gif)
![\begin{aligned}L(y, F_m(x)) &= L(y, F_{m-1}(x) + T(x;\Theta _m)) \\&=-\sum_{i=1}^{N} [y_ilogp_i + (1-y_i)log(1-p_i)] \end{aligend}](http://img.e-com-net.com/image/info8/3e945102487f48b4a4c60533b5d41f0b.gif)
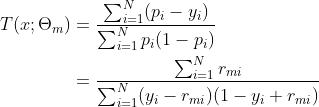
![L(y, F_0(x)) = -\sum_{i=1}^{N} [y_i log p_i + (1-y_i)log(1-p_i)]](http://img.e-com-net.com/image/info8/d8ed3599f7b4496c9305475a422b6218.gif)