超分之VSRT

这篇文章发表于2021年，是Transformer在VSR领域的首篇应用。作者提出了Video Super-Resolution Transformer(VSRT)结构，其由Spatial-temporal Convolutional Self-attention(STCSA)网络和Bidirectional Optical flow-based Feed-forward(BOFF)网络组成。这两个子网络分别解决了经典Transformer欠缺捕捉局部相关性的能力以及前馈神经网络无法完成视频的对齐问题。

参考文档：
①Transformer再下一城！ETH提出：视频超分辨率Transformer
②浅析Transformer训练时并行问题
③真香！Vision Transformer 快速实现Mnist识别
④源码

Abstract

$Q_1$：为什么要将Transformer引入VSR中？
        ~~~~~~~        因为Transformer具有捕捉图片上长距离依赖的特性，其不同于CNN提取局部相关性的能力，它基于自注意力层可以获取全局相关性。CNN在解决视觉任务上，具有较好的归纳偏置，比如善于捕捉局部特性等，但其感受野较小，无法很好的捕捉大范围的特征，因此一般通过加深网络深度来提升感受野，但网络的加深势必带来模型复杂度增加、梯度消失、训练不稳定等问题；而2017年Attention Is All You Need提出的Transformer结构可以捕捉全局相关性，从而让其天然具有较大的感受野，但是其缺陷也很明显，比如较弱的归纳偏置，因此需要大量数据训练，其次不善于捕捉局部相关性等。
        ~~~~~~~        Transformer较大的感受野有利于解决VSR中的大运动问题。大运动问题本质就是相邻帧大幅度的运动使得对齐过程出现较大的不确定性，从而导致难以获取精确的对齐而降低模型重建质量。EDVR中提出了PCD结构，利用多层次不同分辨率来做DCN，由于不同层级的feature map具有不同的特征，因此这些DCN的融合有利于探究复杂、大幅度运动。PCD中随着层级加深，感受野在增加，因此可以捕捉从小到大的运动信息。因此我们也可以使用Transformer来取代PCD加深网络来增加感受野的作用！

---

1. 经典的Transformer无法直接用到VSR中，原因有二：①全连接自注意力层无法利用图像的局部信息，而局部信息对于超分来说是至关重要的；②词前馈层缺乏VSR中最重要的对齐功能。
2. 因此为了解决上述2个问题，作者提出了VSRT结构，这是首篇将Transformer用于VSR的文章。
3. 对于第一个问题，作者提出了Spatial-temporal Convolutional Self-attention(STCSA)网络基于全局相关性的基础上，进一步增加对局部相关性的利用。
4. 对于第二个问题，作者提出了Bidirectional Optical flow-based Feed-forward(BOFF)网络来做基于双向光流的feature-wise对齐。

1 Introduction

经典Transformer的Encoder结构如下：

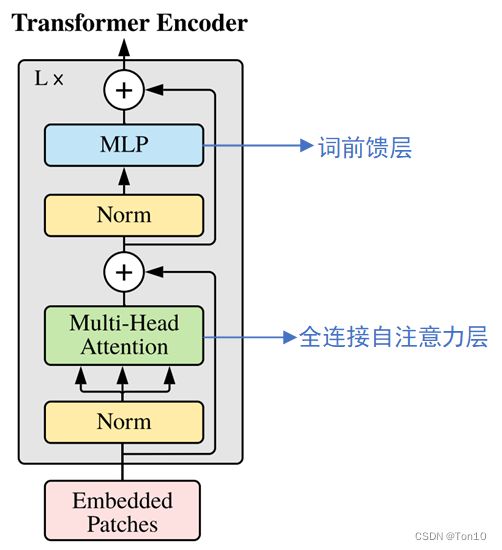
如果我们直接将这个结构硬套到VSR中显然是不行的：

1. 自注意力层虽然可以输出带有全局相关性的特征，但是其缺乏局部相关性：locality对于SISR、VSR来说是至关重要的，因为超分的源图像和目标图像很类似，超分的目的只是恢复出两者之间的细节，而很多细节区域的恢复就需要诸如CNN这种利用图像局部依赖的特性。
2. 词前馈层缺乏对齐的能力：对齐是VSR中不可缺少的一部分，相邻帧无法做到内容对齐那么后续融合超分重建过程就会出错。

---

$自注意力层分析$
①：ViT的出现延申了Transformer在计算机视觉任务上的应用，但是其直接在image-wise上的不重叠分块势必会破坏原图上的一些空间结构，而COLA-Net提出的自注意力模块在feature-wise上按步长为$s$进行重叠分块，这不仅保留了一些空间结构，而且增加了一定的局部相关性。两者的对比如下图所示：

②：此外，现有的视觉上Transformer一般都是取patch，然后flatten成1D的向量，然后使用全连接层获取$Q、K、V$，依靠这种方式来获取全局相关性，但是显然$Q、K、V$中并没有原图上的局部特征信息，因为你获取$Q、K、V$的输入是多个patch展平的结果，它已经不存在图像的局部信息了，所以哪怕你使用了卷积这种局部操作，你获取的只是可学习的注意力参数，而非属于提取原图的局部特征信息。
③：VSR中包含了非常重要的时间信息，因此自注意力层的全局相关性应该不仅只局限于整张image，而应该是整个输入帧序列。这一点在遮挡、边界情景下很有用，因为Transformer具有全局感受野，因此某一帧上的遮挡区域的信息，可以依靠这部分和其他帧之间的相关性重建出来！

$前馈层分析$
经典Transformer的词前馈层对于不同token的处理是相互独立的，不同帧的token之间没有联系，这对于VSR是不行的，因为VSR中的对齐是需要将相邻帧进行内容匹配。
因此想要将前馈层应用于VSR中，就必须在前馈层中设计特征传播和特征对齐两个功能。设计特征传播是为了利用视频序列的双向信息，即过去和未来的特征信息；而设计特征对齐是为了在feature-wise上匹配相邻帧的内容，便于后续的重建。因此必须设计一种新的前馈层来实现特征对齐和特征传播。

---

$文章贡献如下$：

1. 针对自注意力层无法利用局部相关性的问题和时间上的全局依赖问题，作者提出了新的自注意力层结构——Spatial-temporal Convolutional Self-attention(STCSA)网络，具体而言，其通过引入卷积层来使得patch-embedding具有原图上的局部相关性，因此接下来产生的$Q、K、V$就具备了原图上的locality，最后该层输出的feature map就可以带着全局相关性和局部相关性去做对齐。
2. 针对词词前馈层无法解决特征传播和特征对齐问题，作者提出了新的前馈层——Bidirectional Optical flow-based Feed-forward(BOFF)网络，具体而言，使用双向传播机制来做特征传播，使用flow-based的基于feature-wise的对齐来做特征对齐，最后将双向分支的结果进行融合从而传入后续SR重建网络。

2 Related Work

略

3 Preliminary and Problem Definition

$TransformerBlock$：
设${\sigma }_1(\cdot )、{\sigma }_2(\cdot )、\varphi (\cdot )$分别为softmax运算、ReLU激活函数、LN层。
$X\in {\mathbb{R}}^{d\times n}$表示有$d$个维度为$n$的tokens。
整个Transformer Block完成的是${\mathbb{R}}^{d\times n}\to {\mathbb{R}}^{d\times n}$的映射，接下来分别给出全连接自注意力层和词前馈层的数学表达式：
自注意力层：
$$f_1(X)=\varphi (X+\sum _{i=1}^h{W}_o^i(W_v^{i}X)\cdot {\sigma }_1((W_k^{i}X{)}^T(W_q^{i}X))).\text{\hspace{1em}(1)}$$其中$W_v^i,W_k^i,W_q^i\in {\mathbb{R}}^{m\times d}$；$W_o^i\in {\mathbb{R}}^{d\times m}$；$h,+$分别表示head的个数和残差连接。
词前馈层：
$$f_2(X)=\varphi (f_1(X)+W_2{\sigma }_2(W_1\cdot f_1(X)+b_1{1}_n^T)+b_2{1}_n^T).\text{\hspace{1em}(2)}$$其中$W_1\in {\mathbb{R}}^{r\times d},W_2\in d\times r,b_1\in {\mathbb{R}}^r,b_2\in {\mathbb{R}}^d$。

Note：

1. 在VSR中，我们只需要使用Encoder结构作为我们的Transformer块。

4 Video Super-Resolution Transformer

上图就是整个VSR-Transformer(VSRT)的框架结构。
整体由3部分组成：①特征提取；②Transformer块；③重建块。

$特征提取$
该模块由5个残差块组成，主要用于提取浅层特征。

$TransformerBlocks$
该模块是VSRT的核心，本质就是$N$个Encoder模块的级联，每个Transformer Block包含STCSA和BOFF模块，分别用于捕捉时间和空间上长距离上的全局特征相关性(冗余、依赖均可)以及特征传播和特征对齐；此外还包括了残差结构、层归一化LN、position编码。
该模块的输入是一系列输入帧，该模块最后的输出是一系列连续帧，之所以连续是因为对齐过的原因。
Note：

1. $N$为输入帧的个数，Transformer块的个数和帧的个数是一样的，实验中设置为$N=5$。
2. 在BOFF中会使用到30个残差块。
3. 这种输入$N$帧，输出对齐过的$N$帧是区别于之前很多VSR方法——它们每次只输出和参考帧对齐之后的1个支持帧。如果我们把VSR建模成Seq2Seq问题，那么BasicVSR(BasicVSR++)就相当于RNN的做法，而Transformer结构可以免除递归的低效性，而一次性并行处理多帧的对齐问题，这体现了VSRT并行处理的高效性。虽然BasicVSR系列也可以捕捉长距离的特征信息，但是循环结构受限于梯度消失/爆炸、误差累积、信息衰减问题，此外，其每次只输出1帧对齐图像也体现了其低效性。

$重建模块$
重建模块就是一系列残差块的堆积，实验中设置为30个，来进一步提取深层特征信息，最后使用PixelShuffle层来上采样到输出图像。

4.1 Spatial-Temporal Convolution Self-attention

该层的目的就是产生带有局部相关性和全局相关性的feature map(你可以把它近似当成是多层级的CNN提取特征，然后将不同层级特征进行融合的feature map)使得后续对齐的时候可以参考所有帧的特征信息。

想要将全连接自注意力层融入VSR中使用，必须解决2个问题：

1. 在本身捕捉全局相关性的基础上可以利用图像的局部相关性，这对于超分来说是至关重要的。
2. VSR中的时间信息也很重要，因此全局相关性不仅要建立在单张图像上，更要建立在所有输入帧上，即时空注意力。

$Spatial-TemporalConvolutionSelf-attention$
作者设计的时空自注意力层如下所示：

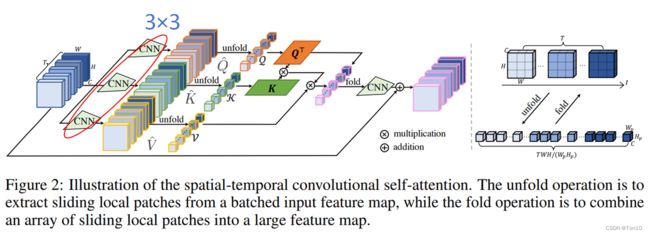
上图就是整体框架，它和COLA-Net提出的自注意力层十分相似，不同之处在于2点：

1. 由于COLA-Net的提出针对图像，所以并没有对时间维度上设置全局注意力，而STCSA设置了时间和空间上的相关性。
2. COLA-Net前端的卷积层设置的是$1\times 1$，而STCSA设置的是$3\times 3$，显然后者可以在图像是捕获更丰富的局部相关性。当然COLA-Net设置$1\times 1$并不是为了增加局部相关性，而是单纯为了产生3组feature map，然后可以分别进行unfold产生patch。

STCSA和ViT中的自注意力层不同之处在于4点：

1. 和ViT最大的不同在于，STCSA自注意力层中的patch是可学习的，并且这些patch已经通过CNN捕捉到了原图的局部相关性，也正是因为这一点使得STCSA可以被用于VSR中。ViT中直接往图中分出patch，然后展平成1D向量，先通过Embedding层处理成固定长度向量，然后使用CNN层输出$\hat{Q}、\hat{K}、\hat{V}$，可以看出虽然使用了卷积这种局部操作，但是其并没有捕获图像的局部相关性，因为卷积的对象早已经不是图像原始的结构了，它已经被flatten、Embedding的操作给破坏掉了。STCSA通过直接在输入feature map上卷积获取局部相关性，这些局部相关性会一直存在于之后的$\mathcal{Q}、\mathcal{K}、\mathcal{V}$中，它们3个会带着这些局部相关性去完成注意力矩阵的计算以及之后的加权和操作，这些保留下来的局部相关性最后会通过Non-Local操作(COLA-Net公式(1))保留在最终的输出中，如此一来最终带有注意力的输出中既有全局相关性又有局部相关性。
2. 它两的第二个差别在于patch的选取对象，ViT是image-wise，而STCSA是feature-wise，后者的做法可以减缓直接对图像分块而造成图像上空间信息的损失，比如线段、物体块等。
3. 第三个不同在于STCSA对时间和空间都设置了全局的注意力。
4. 第四个不同在于获取patch的方式，ViT是直接抽取不重叠的块，而STCSA是以$s$为步长，使用滑动窗口的形式获取patch，显然后者可以进一步增加局部相关性，但是也会带来计算量的增加。

---

接下来我们详细分析STCSA层：
①：首先假设输入为单帧$\mathcal{X}\in {\mathbb{R}}^{T\times C\times H\times W}$；接着使用3个独立的卷积层来获取Query、Key、Value，从而提取了属于$\mathcal{X}$的局部特征：
$$\begin{gathered} \hat{Q}={\mathcal{W}}_q\cdot \mathcal{X}, \\ \hat{K}={\mathcal{W}}_k\cdot \mathcal{X}, \\ \hat{V}={\mathcal{W}}_v\cdot \mathcal{X}.\text{\hspace{1em}(3)} \end{gathered}$$其中${\mathcal{W}}_q、{\mathcal{W}}_k、{\mathcal{W}}_v$为3个卷积层各自的参数，它们都是$3\times 3$，步长为1，填充为1。

②：接下来使用COLA-Net中的unfold算子来获取3D-patch——$d=C\times W_p\times H_p$，其中$W_p、H_p$为patch的宽和高。和ViT按照不重叠的方式取块，作者使用滑动窗口以$s$为步长来获取patch：

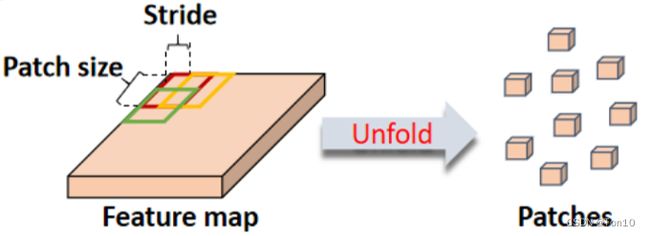
数学表达式为：
$$\mathcal{Q}={\kappa }_1(\hat{Q});\mathcal{K}={\kappa }_1(\hat{K});\mathcal{V}={\kappa }_1(\hat{V}).\text{\hspace{1em}(4)}$$其中${\kappa }_1(\cdot )$表示unfold操作。
Note：

1. 一共获得3组patch，每一组都包含$N$个3D-patch，当$s=W_p$的时候，$N=TWH/W_p{H}_p$；
2. Unfold是对时间和空间都进行操作的，因此最后的全局注意力机制是包含时间和空间的。
3. 每个patch都包含了局部相关性。

③：然后将Query组和Key组的patch进行reshape成2D矩阵的形式：
$$Q=\tau (\mathcal{Q});K=\tau (\mathcal{K}).\text{\hspace{1em}(5)}$$其中$\tau (\cdot )$表示reshape操作；$Q、K\in {\mathbb{R}}^{N\times d}$。

④：将相似度权重和3D-patch的$\mathcal{V}$相乘获取$N$个3D-patch：
$$\begin{gathered} \bar{X}={\sigma }_1(Q{K}^T)\cdot \mathcal{V}, \\ Q{K}^T\in {\mathbb{R}}^{N\times N}.\text{\hspace{1em}(6)} \end{gathered}$$此时的$\bar{X}$既具备局部相关性，又获得了全局相关性；式(5)就是Non-Local操作，用$Q{K}^T$中的每一行的$N$个数分别和$N$个patch相乘并相加成1个新的patch，那么$N$行就会产生$N$个新的patch。

⑤：之后进行fold操作将3D-patch还原成$T\times C\times H\times W$的格式，重叠部分的值通过平均求得，fold操作如下：

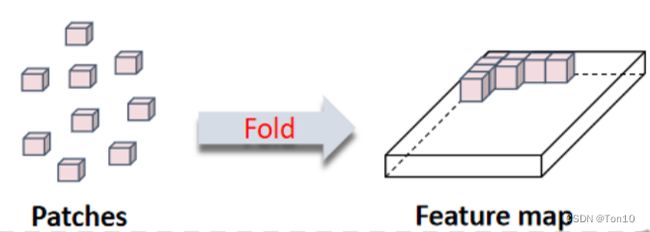
Note：

1. Fold操作是unfold操作的相反运算。

⑥：最后通过一层CNN(即${\mathcal{W}}_o^i$)并使用残差连接获取最终同时带有局部相关性和时空全局相关性的feature map。
这里最后一层CNN一般有2种作用：

1. 将fold结果进行reshape变形调整到输入的size，类似于经典Transformer结构中的多头线性层：

2. 作为可学习层来进一步增加模型非线性度。

---

将上述①~⑥串联起来，并使用LN的整个过程数学表达式如下：
$$f_1(\mathcal{X})=\varphi (\mathcal{X}+\sum _{i=1}^h{\mathcal{W}}_o^i\ast {\kappa }_2(\underset{\mathcal{V}}{{\kappa }_1({\mathcal{W}}_v^i\ast \mathcal{X})}{\sigma }_1(\underset{Q}{{\kappa }_1^{\tau }({\mathcal{W}}_q^i\ast \mathcal{X})}\underset{K^T}{{\kappa }_1^{\tau }({\mathcal{W}}_k^i\ast \mathcal{X}{)}^T}))).\text{\hspace{1em}(7)}$$其中${\kappa }_2(\cdot )$表示fold操作；$W_o^i$表示最后一个卷积层的参数；${\kappa }_1^{\tau }(\cdot )=\tau \circ {\kappa }_1(\cdot )$表示unfold和reshape操作的组合；$f_1(\mathcal{X})\in {\mathbb{R}}^{T\times C\times H\times W}$。

Note：

1. 实验中作者取$h=1$的时候，即单头注意力就可以获取不错的表现力。

---

$Spatial-Temporalpositionalencoding$
Transformer中设置了位置position-embedding来表示token的位置信息，因此本文的VSRT自然也需要位置信息。
具体而言，构建3D的位置编码，包括2个空间位置(水平和垂直)和1个时间位置，其加在STCSA的输入端；这部分位置编码可以通过网络学习也可以使用$sin、cos$函数：
$$PE(pos,i)=\{\begin{array}{l}sin(pos\cdot {\alpha }_k),fori=2k,\\ cos(pos\cdot {\alpha }_k),fori=2k+1.\end{array}\text{\hspace{1em}(8)}$$其中${\alpha }_k=1/10000^{2k/\frac{d}{3}}$；$pos,d$分别是相关维度上的位置坐标和通道序号；$k$是$[0,d/6]$范围内的整数。

4.2 Bidirectional Optical Flow-based Feed-Forward

这里首先解释下特征传播的概念：借用BasicVSR中propagation的概念迁移过来，所谓特征传播就是在当前帧对齐的时候，相邻帧借用过去或未来帧的特征信息来帮助当前的对齐过程；而双向propagation指的是正向分支对齐时，借用过去帧的特征信息来帮助对齐，反向分支对齐时，借用未来帧的特征信息来帮助对齐，最后将两个分支的结果进行融合。

---

Transformer中的词前馈层通过2个$1\times 1$的卷积层(相当于全连接层)和1个ReLU层组成，它们对于不同token的处理是并行但相互独立的，因此无法直接用于对齐不同帧的不同token。为了让前馈层拥有对齐的功能，作者重新设计了词前馈层：

1. 通过引入flow-based的基于feature-wise的双向光流法来利用过去和未来的特征信息来完成对齐。
2. 使用30个残差块来取代原词前馈层的网络结构。
3. 此外作者将$N$帧进行并行对齐，最后直接并行输出$N$帧连续的视频帧。

具体BOFF网络结构如下：

$光流估计$：
BOFF采用了和BasicVSR相同的对齐方式，即flow-based的feature-wise对齐方式，因此必须计算相邻帧的光流信息。在BOFF中，假设输入为5帧，那么2个分支中的光流来自于相邻帧之间的运动估计结果，只不过方向相反。
具体而言，输入$\mathcal{X}\in {\mathbb{R}}^{T\times C\times H\times W}$，其中$T=5$帧，$C=64$，$\mathcal{X}$就是STCSA经过LN和残差结构的输出结果；则分组$G=1$，也就是说对于输出通道$C$的每一帧只学习$G\times 1=1$组光流(包含水平和垂直两个轴)，前向光流和后向光流分别记为$\overrightarrow{O}、\overleftarrow{O}\in {\mathbb{R}}^{T\times 2\times H\times W}$，它们都是通过SPyNet输出得到的。详细的光流计算如上图右边所示，比如说正向分支的时候，光流flow$\in {\mathbb{R}}^{5\times 2\times H\times W}$，也就是说获取了5份光流信息，这5份分别是第0帧和第0帧之间的光流(几乎为0)；第0帧和第1帧之间的光流；第1帧和第2帧之间的光流；第2帧和第3帧之间的光流；第3帧和第4帧之间的光流，反向也是一样的道理：第4帧和第4帧之间的光流；第4帧和第3帧之间的光流；第3帧和第2帧之间的光流；第2帧和第1帧之间的光流；第1帧和第0帧之间的光流。
前向分支：
$$\overrightarrow{O}=\{\begin{array}{l}s(V_{t-1},V_t),ift\in (0,T-1],\\ s(V_0,V_0)ift=0.\end{array}\text{\hspace{1em}(9)}$$后向分支：
$$\overleftarrow{O}=\{\begin{array}{l}s(V_t,V_{t-1}),ift\in [1,T-1),\\ s(V_{T-1},V_{T-1})ift=T-1.\end{array}\text{\hspace{1em}(10)}$$其中$s(\cdot )$为光流估计函数，实验中使用SPyNet，它是预训练好的，然后在BOFF训练时候进行微调；$V_t$表示原始输入序列中的第$t$帧image，即LRS，诸如BasicVSR系列中的光流计算都是基于原始输入序列。

$双向特征对齐$：
运动补偿就是warp的过程，是一个重采样操作。
warp过程2个分支光流的作用对象如下图所示：

比如前向分支的对齐，同时并行完成5帧的对齐：第0帧向第0帧对齐；第0帧向第1帧对齐；第1帧向第2帧对齐；第2帧向第3帧对齐；第3帧向第4帧对齐.反向分支也是同理：同时并行完成5帧的对齐：第4帧向第4帧对齐；第4帧向第3帧对齐；第3帧向第2帧对齐；第2帧向第1帧对齐；第1帧向第0帧对齐。
数学表达式为：
$$\begin{gathered} \overrightarrow{X}=w(\mathcal{X},\overrightarrow{O}), \\ \overleftarrow{X}=w(\mathcal{X},\overleftarrow{O}).\text{\hspace{1em}(11)} \end{gathered}$$其中$\overrightarrow{X}、\overleftarrow{X}$分别为$\mathcal{X}$经过warp函数$w(\cdot )$之后的正向对齐feature map和反向对齐feature map。
源码为：

# x1:[B, 5, 64, 64, 64]
# flow1:[B*5, 64, 64, 2]
x1 = flow_warp(x1.view(-1, c, h, w), flow1)  # 反向
# x2:[B, 5, 64, 64, 64]
# flow2:[B*5, 64, 64, 2]
x2 = flow_warp(x2.view(-1, c, h, w), flow2)  # 正向

$双向特征传播$：

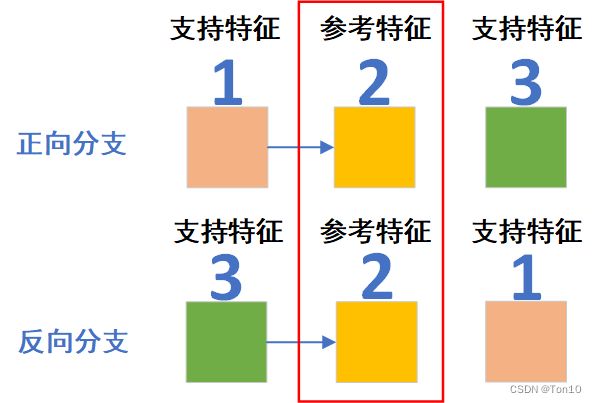
如上图所示是正反向分支2个相邻帧1和帧3向帧2对齐的示意图：
正向分支：对帧1做对齐的时候，由于其是STCSA的输出，因此特征内包含了过去和未来所有时间维度和空间维度上的特征信息，但可以理解为此时的feature map1中以帧1本身的特征信息为主(相似度较大)，全局相关的特征信息为次(相似度较小)，因此可以看成是正向特征传播过程。这一点和BasicVSR的propagation是非常类似的，只不过它是因为经过不断地传播导致特征信息衰减了，最后对齐的时候以当前帧为主，越是往前的特征信息衰减的越厉害。
反向分支：对帧3做对齐的时候，由于其是STCSA的输出，因此特征内包含了过去和未来所有时间维度和空间维度上的特征信息，但可以理解为此时的feature map3中以帧3本身的特征信息为主(相似度较大)，全局相关的特征信息为次(相似度较小)，因此可以看成是反向特征传播过程。这一点和BasicVSR的propagation是非常类似的，只不过它是因为经过不断地传播导致特征信息衰减了，最后对齐的时候以当前帧为主，越是往后的特征信息衰减的越厉害。

Note：

1. 其实VSRT提出的双向特征传播的本质和BasicVSR系列的并不同，后者引入双向分支的目的在于在利用全局信息的基础上解决不同位置帧利用信息的公平性问题；而在前者中，BOFF中每一帧代表的输入特征都具备了全局特征信息，故每一帧代表的feature map在对齐的时候，是不存在信息的利用不对等问题；所以VSRT利用的双向特征传播本质上和EDVR、TDAN这些local方法是一样的，即让前后相邻支持feature map和当前参考feature map对齐，但有区别的是，VSRT每一个feature map都包含所有帧的全局特征信息，BOFF具体示意图如下所示：

$前馈层和融合$：
①前馈层：对齐之后的输出需要经过前馈层进行refine，这其实是一个特征校正的过程，在TDAN(使用CNN)、BasicVSR系列(使用残差块)中都有。这种对齐之后的卷积层一般有4个作用：

1. 将feature-wise转变的image-wise，和输入端的CNN相反。
2. 对对齐特征进行校正调整，减少特征上artifacts的出现。
3. 在BasicVSR中出现，将其他特征信息和对齐特征进行融合，并通过特征校正模块进行信息填充或缺失信息弥补。
4. 作为Transformer中的前馈层。

Note：

1. 在文中进入前馈层的输入不仅仅是对齐feature map，而是对齐feature map和输入序列$\mathcal{V}$的concat——$[\mathcal{V},\overrightarrow{X}/\overleftarrow{X}]$，这个过程的张量size为$[B\ast T,(64+3),H,W]$。

②融合：借鉴BasicVSR的做法，最后通过融合将两个分支的对齐结果进行合并，融合过程是将正向和反向的feature map进行concat，然后使用一层卷积层来压缩一半的通道。

---

综上所述，我们将整个BOFF模块使用数学表达式：
$$f_2(\mathcal{X})=\varphi (\mathcal{X}+\rho (\overleftarrow{W_1}\ast {\sigma }_2(\overleftarrow{W_2}\ast [\mathcal{V},\overleftarrow{X}])+\overrightarrow{W_1}\ast {\sigma }_2(\overrightarrow{W_2}\ast [\mathcal{V},\overrightarrow{X}])\left)\right).\text{\hspace{1em}(12)}$$其中$\rho (\cdot )$表示融合过程；$(\overrightarrow{W_1}、\overrightarrow{W_2})、(\overleftarrow{W_1}、\overleftarrow{W_2})$分别表示前向分支上2个全连接层的参数和后向分支上2个全连接层的参数；$\mathcal{V}=\{V_0,\cdots ,V_{T-1}\}$表示输入序列LRS，这部分缺一不可，因为它们将作为参考帧序列，和相对应的对齐feature map做融合。
作者接下来对这个2层的前馈层进行扩展修改，用30个残差块来代替，记为$R_1(\cdot ),R_2(\cdot )$，因此式(12)可以改成：
$$f_2(\mathcal{X})=\varphi (\mathcal{X}+\rho (R_1([\mathcal{V},\overrightarrow{X}])+R_2([\mathcal{V},\overleftarrow{X}]))).\text{\hspace{1em}(13)}$$
Note：

1. 前馈层的选择是多样的，可以是残差块，也可以是其他CNN结构。

比起BasicVSR使用递归循环结构去做光流估计和运动补偿，本文提出的VSRT可以避免递归而可以并行进行对齐操作！

5 Experiments

$Datasets$：
①训练集：REDS中除了000、011、015、020四个clips之外的266个视频数据；Vimeo-90K(4278个视频89800个clips)。
②验证集：REDS中除了000、011、015、020四个clips之外的266个视频数据。
③测试集：Vid4、Vimeo-90K-T、REDS中000、011、015、020四个clips。

$Evaluationmetrics$：
PSNR、SSIM、model-sizes。

$Evaluationmetrics$：

1. 每次输入序列长度为5帧。
2. Batch=2。
3. patch为$64\times 64$。
4. Transformer块的个数为输入帧的个数。
5. 光流估计使用SPyNet。
6. 数据增强使用水平翻转和90°旋转。
7. 训练的iterations为60W次，使用Adam+CA。
8. 使用Charbonnier损失函数。
9. 浅层特征提取的残差块为5个；BOFF中为前后分支$R_1、R_2$各为30个；重建模块中的残差块为30个，输出通道均为64。
10. 关于VSRT整个网络参数如下：

5.1 Results on REDS

为了平等使用相同的信息，作者将BasicVSR和IconVSR的输入帧都设置为5帧。VSRT和其他VSR方法在REDS4上的对比结果如下：

实验结论如下：

1. 当输入为短帧的时候，BasicVSR系列的表现力下滑严重，甚至连EDVR都比不上，这证明了BasicVSR系列方法的高表现力建立在较长序列输入上。
2. VSRT基于Transformer结构可以取代RNN的递归结构来建模VSR问题为Seq2Seq问题，证明了其可适用于长序列VSR，但在短帧上，其表现力仍然要比递归结构的BasicVSR要好，当然代价也很明显，就是模型参数量的增加。

可视化结果如下：

5.2 Results on Vimeo-90K

VSRT和其他VSR方法在Vimeo-90K-T和Vid4上的对比结果如下：

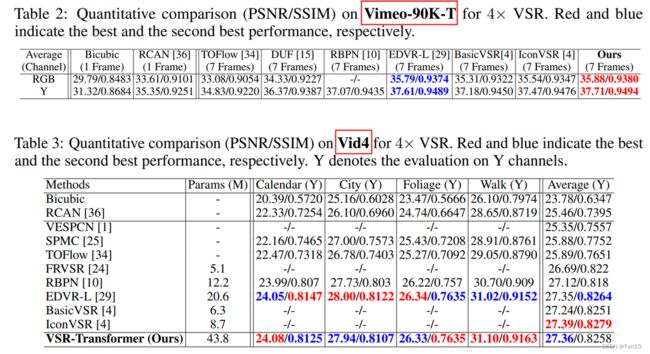
从Vid4上的结果来看，VSRT的PSNR要比BasicVSR系列要低，这是因为IconVSR是在全序列上的(平均30~40帧)，而VSRT是7帧。下图是7帧上的表现力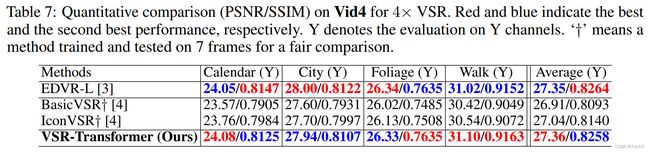：从实验的结果来看BasicVSR系列性能下降，进一步说明了BasicVSR高性能依赖于长序列的信息。

可视化结果如下：

5.3 Ablation Study

$STCSA$
为了探究STCSA的有无为VSRT带来的性能变化，作者删去了STCSA层和完整的VSRT做对比，实验结果和可视化如下：

$BOFF$
为了探究BOFF的有无为VSRT带来的性能变化，作者删去了BOFF层，改用残差块来代替，实验结果和可视化结果如下：

$NumberofFrames$
为了探究输入帧个数对VSRT性能的影响，作者进行了3帧和5帧的对比试验，实验结果如下：

6 Conclusion

1. 本文提出了1个将Transformer引入VSR中的网络结构——VSRT。这是首篇Transformer在视频超分上的使用，它主要由时空卷积自注意力网络(STCSA)和双向光流前馈网络(BOFF)组成。
2. STCSA在COLA-Net提出的自注意力网络的基础上进一步引入图像的局部相关性需求以及时间和空间上的全局相关性，从而为Transformer引入VSR中创造了必要的条件。
3. BOFF借鉴BasicVSR的特征传播和特征校正机制来设计出适合VSR的新前馈层结构，但不同于递归结构，其并行化处理所有输入帧信息，其利用SPyNet计算双向光流来对feature做对齐。