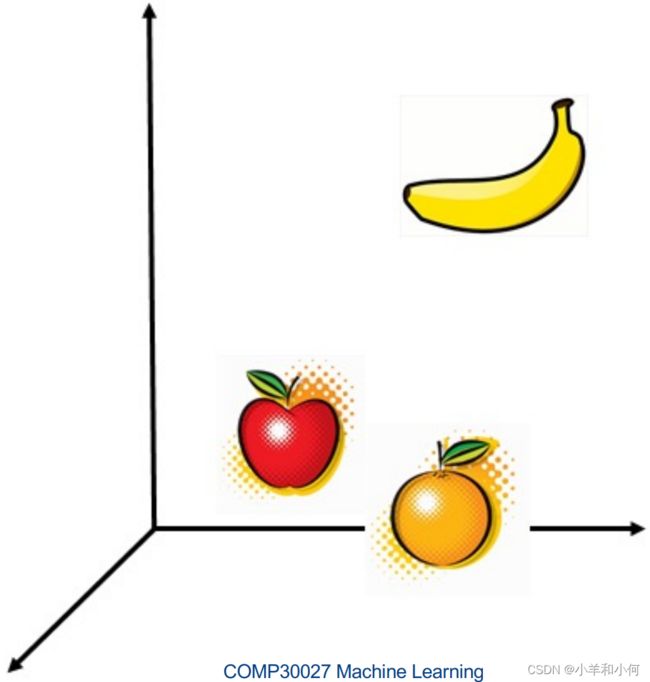
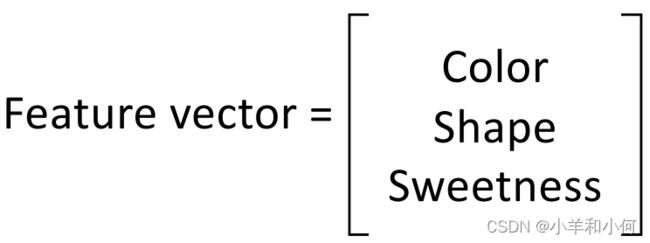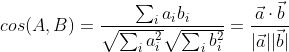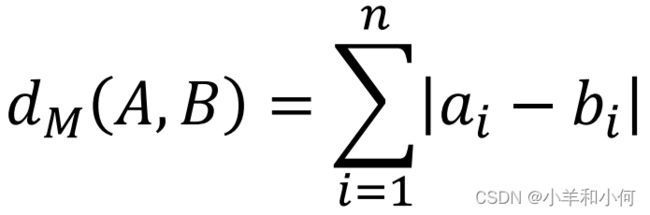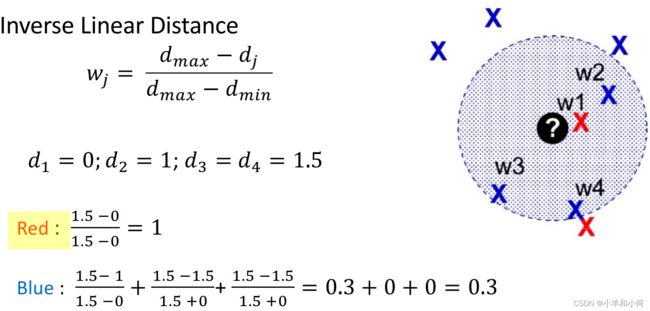机器学习基础:基于样本的学习——KNN
目录
1. 基于样本的学习
2. 比较样本
2.1 特征向量
2.2 特征向量的度量(Similarity / Distance)
2.2.1 特征向量的度量——向量
2.2.2 特征向量的度量——距离
2.2.3 特征向量的度量——非数值型距离
3. Instance-Based 分类器
3.1 最近邻分类器(Nearest Neighbor Classifier)
3.2 K最近邻(K-Nearest Neighbor)算法(KNN)
3.3 加权(Weighted KNN)
3.4 不同加权KNN示例
3.5 KNN的复杂度分析
3.6 KNN与Naive Bayes/Decision Tree的比较
1. 基于样本的学习
对于一个机器学习系统,输入有下面三个方面的内容组成:
- 样本 (instance)
- 特征(attributes / features)
- 标签 (classes / labels)
什么是样本:
对监督学习来说,每个样本可以看做是一个包含
个特征的元组同时拥有一个表明类别的标签。
机器学习的目的:
根据数据提供的
标签,试图构建一个模型,这个模型可以代表整个数据集的输入和输出关系。
基于样本的学习(instance-based learning):
需要将进行标注的
保存在内存中,直接从
中学习(而不建立任何的模型),也称为
。
2. 比较样本
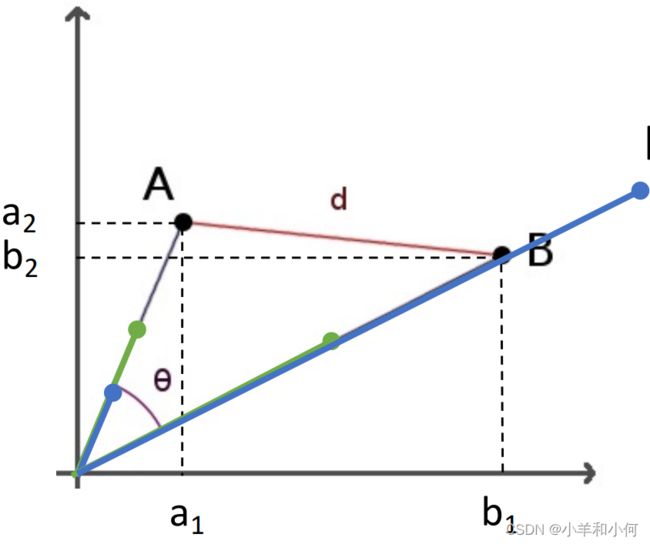
如何比较样本(Comparing Instances)呢?
对于每个![]() ,因为它的特征是一个
,因为它的特征是一个![]() 元组,那么我们总是可以把这个
元组,那么我们总是可以把这个![]() 元组看成是一个向量
元组看成是一个向量![]() 。
。
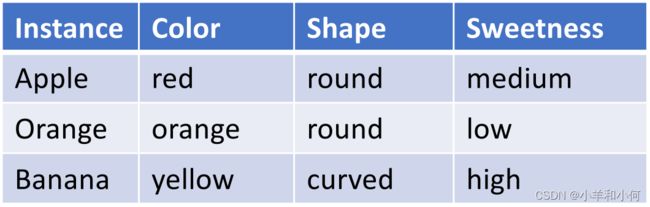
2.1 特征向量
特征的类型:
: 例如颜色,性别。
: 这类特征是有严格顺序的,例如描述温度程度的特征
。
: 这种是连续的数值特征:例如身高、体重、年龄。
特征向量根据之前的描述,我们可以看做一个![]() 元组,那么我们可以将描述这个向量的
元组,那么我们可以将描述这个向量的![]() 维空间看做是向量的特征空间。通过这种方式,我们可以衡量任意两个具有相同维度的特征向量的相似度、长度等很多指标来实现对向量定量计算和判断的目的。
维空间看做是向量的特征空间。通过这种方式,我们可以衡量任意两个具有相同维度的特征向量的相似度、长度等很多指标来实现对向量定量计算和判断的目的。
2.2 特征向量的度量(Similarity / Distance)
2.2.1 特征向量的度量——向量
相似度 (Similarity)
两个向量的相似度:衡量两个向量之间有多像。
相似度的值越大代表相似度越高。通常相似度的取值范围在
之间
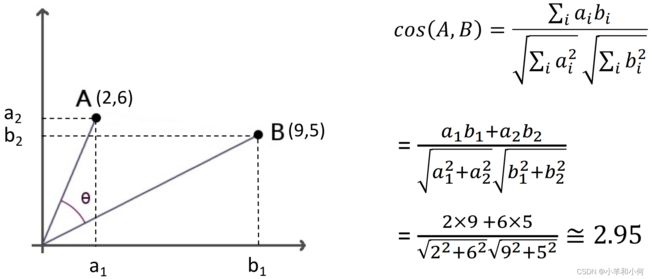
余弦相似度(Cosine Similarity)
2.2.2 特征向量的度量——距离
距离(Distance)
两个向量之间的距离
:
衡量两个向量之间有多不像,
越小表明两个向量越像 ,两个向量的最小距离是
。
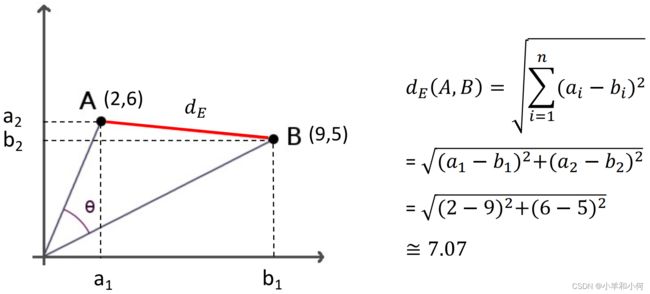
欧几里得距离 (Euclidean Distance)
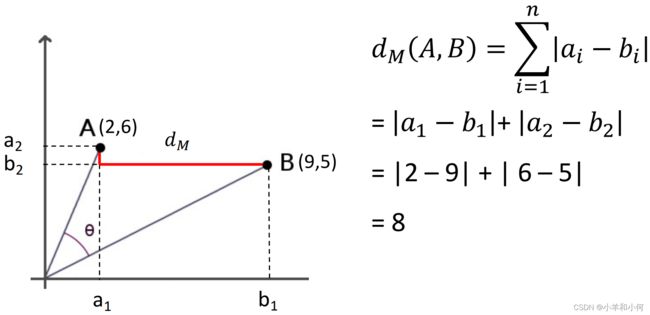
曼哈顿距离(Manhattan Distance)
2.2.3 特征向量的度量——非数值型距离
Hamming距离
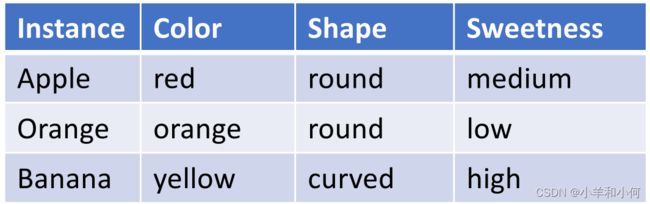
上面说的两个特征向量距离的度量方式必须要求每一个维度的特征都要是数值类型的,那么如果对于下面这种包含![]() 类型的
类型的![]() 之间,如何衡量
之间,如何衡量![]() 。首先应该将所有的
。首先应该将所有的![]() 特征都使用
特征都使用![]() 编码的方式进行转换。
编码的方式进行转换。
:
就是一种将非数值特征转换成数值特征的方式。而且能够保证特征在转换之后,不同的取值在距离上都是完全一样的。
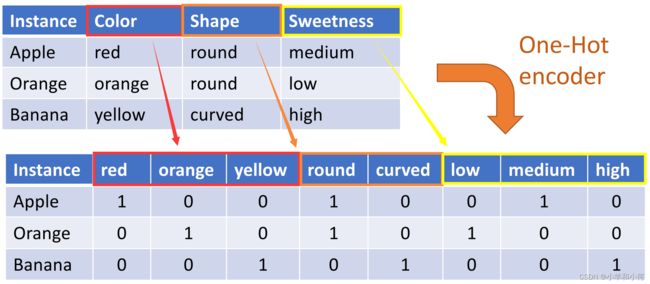
例如![]() 这列特征,在进行
这列特征,在进行![]() 编码之后,所有的特征取值都变成了用
编码之后,所有的特征取值都变成了用![]() 个位表示的向量;无论是
个位表示的向量;无论是![]() 和
和![]() 还是
还是![]() 和
和![]() 或是
或是![]() 和
和![]() 之间,都只有一个
之间,都只有一个![]() 位的不同,因此他们相互之间都是公平的。
位的不同,因此他们相互之间都是公平的。
如果不用![]() 可能会造成一种不公平的现象。假设还是对
可能会造成一种不公平的现象。假设还是对![]() ,我们让
,我们让![]() ,
,![]() ,
, ![]() ;看起来他们之间还是彼此距离一样,但其实有一个问题,就是对机器来说,很可能认为
;看起来他们之间还是彼此距离一样,但其实有一个问题,就是对机器来说,很可能认为![]() 的优先级高于
的优先级高于![]() 和
和![]() ,因为
,因为![]() 的数值较大。而使用
的数值较大。而使用![]() 就可以完美解决这个问题
就可以完美解决这个问题
存在的问题:
但是
问题就是会造成特别系数的矩阵。对于
来说
个颜色还好,如果有一个特征有
种不同的取值,那么通过
编码出的新特征就会是一个长度为
的值,里面除了某一个
位上的值
之外,其他
个位置都是
。这个矩阵就过于稀疏了。
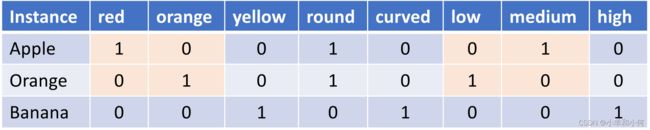
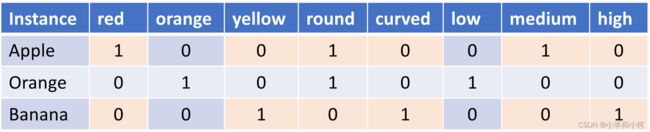
经过![]() 编码之后我们就可以衡量两个样本之间的距离了:
编码之后我们就可以衡量两个样本之间的距离了:
从图中可以看出![]() 样本和
样本和![]() 之间有
之间有![]() 个
个![]() 位是不同的,因此他们的距离就是
位是不同的,因此他们的距离就是![]() ,而
,而 ![]() 和
和![]() 的距离是
的距离是![]() 。
。
![]()
![]()
3. Instance-Based 分类器
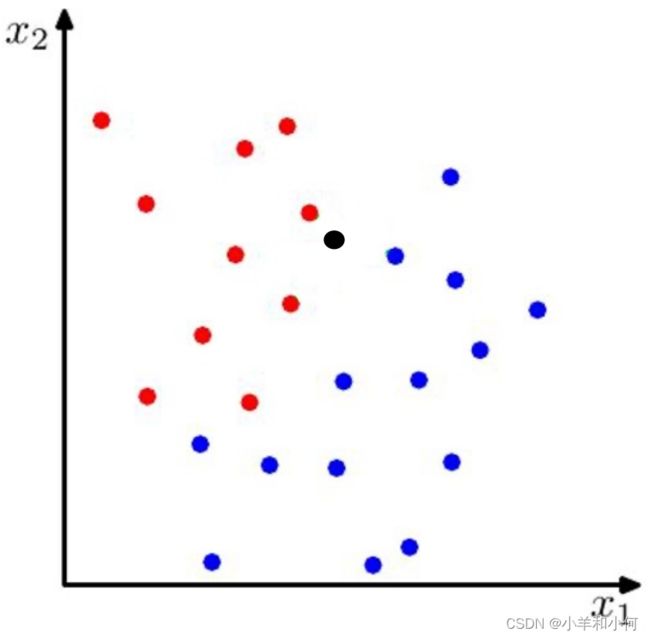
3.1 最近邻分类器(Nearest Neighbor Classifier)
基于的假设:空间中两个样本的距离越相近,那么他们越可能拥有相同的标签。
算法细节:
对于一个样本![]() (测试样本,没有
(测试样本,没有![]() ),离他最近的一个训练样本(有
),离他最近的一个训练样本(有![]() 的样本)是
的样本)是![]() ,它所有的邻居样本是
,它所有的邻居样本是![]() ;在所有邻居样本中通过距离/相似度测算得到距离最小或者相似度最大的邻居样本:
;在所有邻居样本中通过距离/相似度测算得到距离最小或者相似度最大的邻居样本:
![]()
用这个最近邻居样本的![]() 作为当
作为当![]() 的
的![]() 。
。
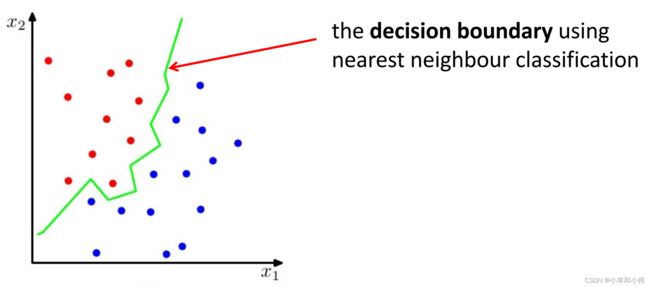
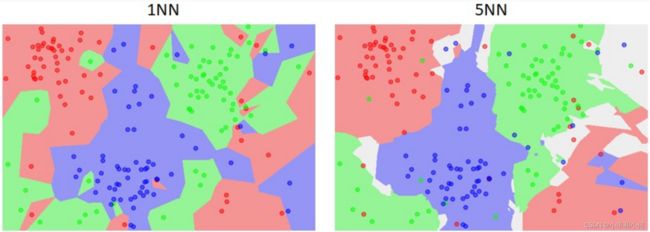
通过最近邻算法得到的决策边界是非线性的:
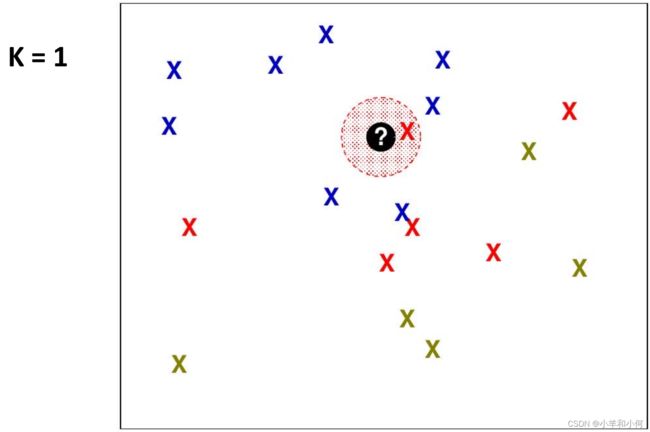
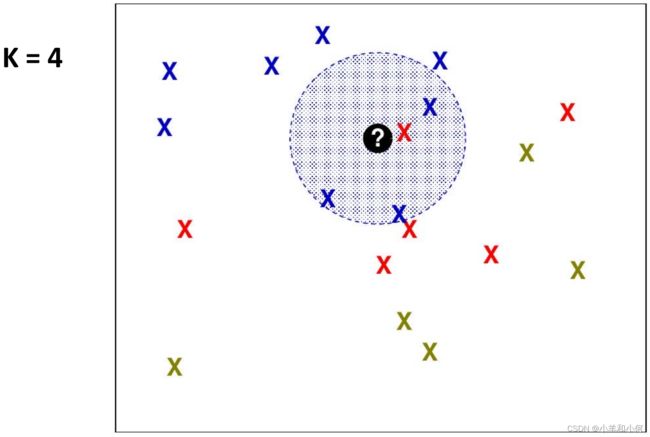
3.2 K最近邻(K-Nearest Neighbor)算法(KNN)
最近邻是通过找最近的一个带标签的训练样本![]() ,把
,把![]() 的标签当做自己的预测标签,将一个邻居扩展到
的标签当做自己的预测标签,将一个邻居扩展到![]() 个邻居,也就是通过
个邻居,也就是通过![]() 个训练样本的标签来决定当前这个预测样本的标签,这样的算法叫
个训练样本的标签来决定当前这个预测样本的标签,这样的算法叫![]() 最近邻。
最近邻。
如何选择![]() :不同的
:不同的![]() 会导致算法的表现差异很大。
会导致算法的表现差异很大。
 值越小,由于对噪声过拟合,分类器性能越低,泛化能力越差。
值越小,由于对噪声过拟合,分类器性能越低,泛化能力越差。- 当
 很大的时候
很大的时候 值越大,分类器性能越趋向于
值越大,分类器性能越趋向于 的性能;因为
的性能;因为 其实可以看成将所有的样本数
其实可以看成将所有的样本数 一起考虑的
一起考虑的 -最近邻。
-最近邻。 - 一般来说,对训练数据进行试错是得到合适
 的唯一方法。
的唯一方法。 - 我们需要考虑数据点的密度。
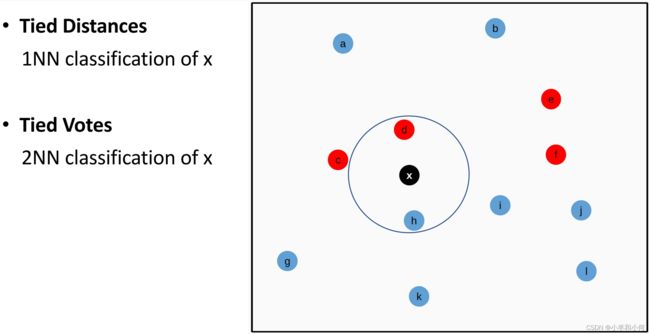
打破平局
一定会出现一种情况,假设是![]() -最近邻,但在当前需要预测样本
-最近邻,但在当前需要预测样本![]() 的周围恰好有两个标签不同的样本
的周围恰好有两个标签不同的样本![]() ,
,![]() 距离
距离![]() 完全相同。
完全相同。
打破平局的方式有
种:
- 随机选一个
- 选哪个具有更高先验概率的样本:例如
的类别标签是
,
的类别标签是
,而在整体的训练集的样本分布中,标签为
的样本占了
,
的样本占了
,这时候以
为标签的样本的先验概率就是
所以这时候
的标签为
。
- 将当前的
增加到
。
3.3 加权 (Weighted KNN)
(Weighted KNN)
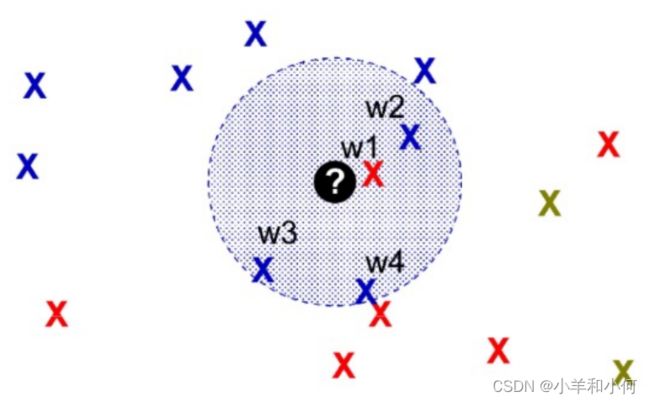
假设在这种情境中,对于一个样本![]() 周围有多个样本点,如果按照传统的
周围有多个样本点,如果按照传统的![]() 就会判定
就会判定![]() 的标签和蓝色的样本一样。但明明有一个红色的样本点离这个
的标签和蓝色的样本一样。但明明有一个红色的样本点离这个![]() 比其他的所有蓝色样本点都更近,这样的情景我们应该怎么处理呢?
比其他的所有蓝色样本点都更近,这样的情景我们应该怎么处理呢?
给数量和距离都分配一定的权重,最后得到的加权值比较大的样本类作为![]() 的标签。
的标签。
加权![]() 使用的加权策略有以下常用的三种:
使用的加权策略有以下常用的三种:
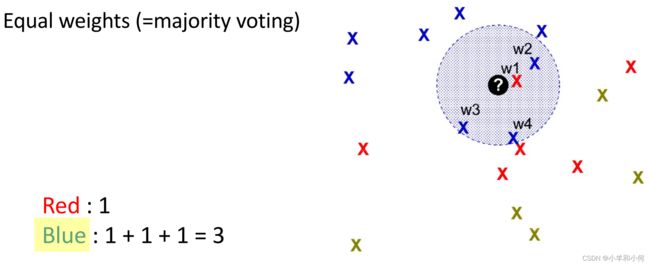
平等权重(Equal weight)
这种方式就是传统的![]() ,即
,即![]() 周围的每个样本点权重都一样,哪个类标签的样本数多就把
周围的每个样本点权重都一样,哪个类标签的样本数多就把![]() 分为哪一类。
分为哪一类。
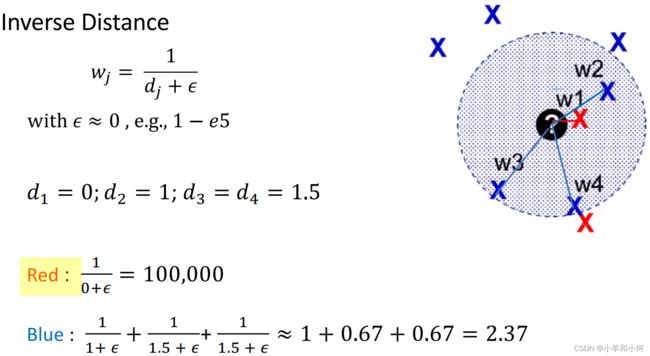
距离倒数(Inverse distance)
每个![]() 周围的样本
周围的样本![]() ,他们与
,他们与![]() 之间的距离表示为
之间的距离表示为![]() ,那么他们的权重分别是:
,那么他们的权重分别是:
其中![]() 是一个非零但是极小的值,为了避免
是一个非零但是极小的值,为了避免![]() 。
。
计算过程中出现了除![]() 问题。
问题。
存在的问题:
离
近到一定程度的样本的倒数会非常大,大到哪怕其他类在附近的样本很多也可以忽略不计。
缩放的距离倒数(Inverse linear distance)
通过这种放缩方式可以保证没有非常大的值出现。
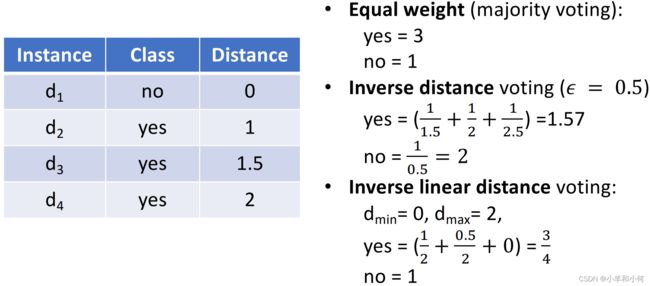
3.4 不同加权KNN示例
3.5 KNN的复杂度分析
因为这是一种![]() (
(![]() )的计算方式,因此需要非常暴力地对所有的样本同时加载到内存中进行计算。
)的计算方式,因此需要非常暴力地对所有的样本同时加载到内存中进行计算。
对于一个包含![]() 个样本,每个样本
个样本,每个样本![]() 个特征的数据集,这种算法的复杂度为
个特征的数据集,这种算法的复杂度为![]() 。
。
对于规模较小的数据集,这种方法效果很好。
但对于大数据集,几乎不考虑这种方法。
3.6 KNN与Naive Bayes/Decision Tree的比较
![]() 是一种非常
是一种非常![]() 的算法,因为它不存在训练,所有的操作都在测试阶段完成,所以
的算法,因为它不存在训练,所有的操作都在测试阶段完成,所以![]() 不存在需要训练的参数.
不存在需要训练的参数.
给定一个![]() 个类别,
个类别,![]() 个不同特征的数据集,对于一个
个不同特征的数据集,对于一个![]() 样本,
样本,![]() 需要的计算时间为
需要的计算时间为![]() ,而
,而![]() 只需要
只需要![]() 。
。
![]() 的优点:
的优点:
- 简单,基于样本,不需要建立模型。
- 可以产生很灵活的决策边界。
- 可以随时增加新的训练或者测试样本而不用重新生成模型。
![]() 的缺点:
的缺点:
- 需要规划一个很好的距离函数才能最大发挥算法的性能
- K 值需要自己设定
- 所有的计算都发生在预测阶段,不可能预先训练模型并保存使用
- 容易受到噪音干扰,在高维数据上很难应用