相机标定—— 张正友标定法（1）

一、相机标定的目的

我们首先要明白两个问题：1、相机是如何成像的？2、相机标定的目的是什么？

1. 相机的成像过程与坐标系的转换

相机的成像过程涉及了 4 种坐标系与 3 种变换关系，这 3种变换关系分别是刚体变换、投影变换和离散化。

$$图1：四种坐标系的关系$$

构建世界坐标系只是为了更好的描述相机的位置在哪里，在双目视觉中一般将世界坐标系原点定在左相机或者右相机或者二者X轴方向的中点。

接下来讲一讲关于这几个坐标系的转换。也就是说，一个现实中的物体是如何在图像中成像的。

1.1.1 世界坐标系与相机坐标系之间的转换

从世界坐标系到相机坐标系，涉及到旋转和平移（其实所有的运动也可以用旋转矩阵和平移向量来描述）。绕着不同的坐标轴旋转不同的角度，得到相应的旋转矩阵，如下图所示：
相机发生安装误差时，会导致相机坐标系发生旋转和平移若相机的绕Z轴旋转的角度为$\theta$,旋转后P点的坐标为$\mathrm{p}\left(x^{\prime },y^{\prime },z^{\prime }\right)$—（世界坐标系），用没旋转前的坐标系—（相机坐标系）表示为：

那么从世界坐标系到相机坐标系的转换关系如下所示：

具体而言：
$$\left[\begin{array}{c}{X}_c\\ Y_c\\ Z_c\end{array}\right]=\mathbf{R}\left[\begin{array}{c}{X}_w\\ Y_w\\ Z_w\end{array}\right]+\mathbf{T}=\left[\begin{array}{lll}{r}_{11}& r_{12}& r_{13}\\ r_{21}& r_{22}& r_{23}\\ r_{31}& r_{32}& r_{33}\end{array}\right]\left[\begin{array}{l}{X}_w\\ Y_w\\ Z_w\end{array}\right]+\left[\begin{array}{c}{t}_x\\ t_y\\ t_z\end{array}\right]（1.1）$$
公式(1.1)中的 R 为3X3的单位正交矩阵，T 为 3 个方向上的平移向量，其中 R 满足以下约束关系：
$$\{\begin{array}{l}{r}_{11}^2+r_{21}^2+r_{31}^2=1\\ r_{12}^2+r_{22}^2+r_{32}^2=1\\ r_{13}^2+r_{23}^2+r_{33}^2=1\end{array}$$
为计算方便将式(1.1)改写成齐次坐标形式：
$$\left[\begin{array}{l}{X}_c\\ Y_c\\ Z_c\\ 1\end{array}\right]=\left[\begin{array}{ll}\mathbf{R}& \mathbf{T}\\ 0^T& 1\end{array}\right]\left[\begin{array}{l}{X}_w\\ Y_w\\ Z_w\\ 1\end{array}\right]=\mathbf{M}\left[\begin{array}{c}{X}_w\\ Y_w\\ Z_w\\ 1\end{array}\right](1.2)$$
公式(1.2)中， M 为 4X4 矩阵，描述了从世界坐标系到摄像机坐标系的变换过程。

1.1.2相机坐标系与图像坐标系

从相机坐标系到图像坐标系，属于透视投影关系，从3D转换到2D。

此时投影点p的单位还是连续的mm，并不是pixel，需要进一步离散化到像素坐标系。

1.1.3图像坐标系与像素坐标系

像素坐标系和图像坐标系都在成像平面上，只是各自的原点和度量单位不一样。图像坐标系的原点为相机光轴与成像平面的交点，通常情况下是成像平面的中点或者叫principal point。图像坐标系的单位是mm，属于物理单位，而像素坐标系的单位是pixel，我们平常描述一个像素点都是几行几列。所以这二者之间的转换如下：其中dx和dy表示每一列和每一行分别代表多少mm（dx 和dy 分别表示单个像素元在 x 轴和 y 轴的物理尺寸），即1pixel=dx mm

那么通过上面四个坐标系的转换就可以得到一个点从世界坐标系如何转换到像素坐标系的。

通过最终的转换关系来看，一个三维中的坐标点，的确可以在图像中找到一个对应的像素点，但是反过来，通过图像中的一个点找到它在三维中对应的点就很成了一个问题，因为我们并不知道等式左边的Zc的值。

2. 相机标定的目的和双目测距（深度）的原理

当我们拿到一张图片，进行识别之后，得到的两部分之间的距离为多少像素，但是这多少像素究竟对应实际世界中的多少米呢？这就需要利用相机标定的结果来将像素坐标转换到物理坐标来计算距离（当然这里值得说明，仅仅利用单目相机标定的结果，是无法直接从像素坐标转化到物理坐标的，因为透视投影丢失了一个维度的坐标，所以测距其实需要双目相机）。
为什么单目摄像机不能测深度？
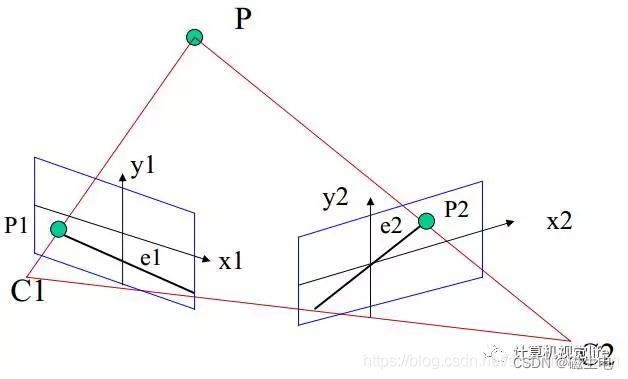
下图从物理原理上展示了为什么单目相机不能测量深度值而双目可以。我们看到红色线条上三个不同远近的黑色的点在下方相机上投影在同一个位置，因此单目相机无法分辨成的像到底是远的那个还是近的那个。

视差的概念：是指从两个不同位置观察同一个物体时，此物体在视野中的位置变化与差异。从两个观察点看目标，两条视线之间的夹角叫做这两个点的视差角，两点之间的距离称作视差基线。在立体匹配前左右视图已经进行了立体校正，这时候左右视图对应像素点只存在 X 轴方向上的差异，因此立体匹配只需要在X 轴上进行搜索,这时我们称三维世界中的一个特征点在左右视图 X轴方向的位置差异称为视差，视差用 d 表示。

双目立体视觉深度相机测距流程：
(1）需要对双目相机进行标定，得到两个相机的内外参数、单应矩阵。
(2) 根据标定结果对原始图像进行校正，校正后的两张图像位于同一平面且互相平行。
(3）对校正后的两张图像进行像素点匹配。
(4）根据匹配结果计算每个像素的深度，从而获得深度图

理想双目相机成像模型：
首先我们从理想的情况开始分析：假设左右两个相机位于同一平面（光轴平行），且相机参数（焦距f)一致。那么深度值的推到原理和公式如下：
测距系统主要由 5 个子模块组成：图像采集、立体标定、立体校正、立体匹配和深度信息获取。
立体标定的主要目的是求解出双目相机的所有内外参数，同时内外参数的求解是后续进行立体校正的基础。

根据三角形相似性得到：
$$\frac{Z}{f}=\frac{X}{Xl}$$

$$\frac{z}{f}=\frac{x-b}{xr}$$

$$\frac{z}{f}=\frac{y}{yl}=\frac{y}{yr}$$
Depth
$\mathrm{z}={\mathrm{f}}^{\ast }\mathrm{b}/(\mathrm{x}\mathrm{l}-\mathrm{x}\mathrm{r})={\mathrm{f}}^{\ast }\mathrm{b}/\mathrm{d}$
$x=x{l}^{\ast }z/f$ or $b+x{r}^{\ast }z/f$
$y=y{l}^{\ast }z/f$ or $y{r}^{\ast }z/f$

$Y$-axis is perpendicular to the page.

上式的 $\mathrm{x}\mathrm{l}-\mathrm{x}\mathrm{r}$就是视差，用d表示，所以知道视差了就可以求得深度Z。

根据上述推导，空间点p离相机的距离（深度）为：z=f*b/d，可以发现如果要计算深度z，必须要知道：
(1）相机焦距f，左右相机基线b。这些参数可以通过先验信息或者相机标定得到。
(2）视差b。需要知道左相机的每个像素点（Xl, Yl）和右相机中对应点（Xr，Yr）的对应关系。这是双目视觉的核心问题：像素点匹配。

极限约束
那么问题来了，对于左图中的一个像素点，如何确定该点在右图中的位置？可以通过极限约束。
什么是极线呢？如下图所示，C1，C2是两个相机，p是空间中一点，P和两个相机中心点C1、C2形成了三维空间中的一个平面PC1C2，称为极平面。极平面和两幅图像相交于两条直线，这两条直线为极线。p在相机C1中的成像点是P1，在相机C2中的成像点是P2，但p的位置事先是未知的。
我们的目标是：对于左图中的P1点，寻找它在右图中的对应点P2，这样就能确定P点的空间位置，也就是我们想要的空间物体和相机的距离。

所谓极线约束，就是指当同一个空间点在两幅图像上分别成像时，已知左图投影点P1，那么对应右图投影点P2一定在相对于P1的极线上，这样可以极大的缩小匹配范围。


细心的朋友会发现上述过程考虑的情况（两相机共面且光轴平行，参数相同）非常理想，相机C1、C2如果不在同一直线上怎么办？

非理想双目相机成像模型
事实上，这种情况非常常见，因为有些场景下两个相机需要独立固定，很难保证光心C1、C2完全水平，即使是固定在同一基板上也会因为装配的原因导致光心不水平。

有办法哟！

我们先来看看这种情况下拍摄的两张左右图片，左图中三个十字标志的点，在右图中对应的极线是右图中的三条白线，也就是对应的搜索区域。我们看到这三条线并不是水平的，如果进行逐点搜索效率非常低，因为搜索的是一个二维的搜索，把斜线转换为水平线就可以进行一维搜索。
怎么办呢？
把不理想的转化为理想情况就好了。这就是图像矫正技术。

图像校正技术是通过分别对两张图片用单应矩阵变换 得到的，目的就是把两个不同方向的图下个平面重新投影到同一平面且光周相互平行，下图中的黄色平面，这样就可以用前面理想情况下的模型了，两个相机的极线也变成水平的了。

经过校正后，从上图中我们可以看到越远的物体视差越小，越近的物体视差越大，和我们的常识一致。
上面讲到的对于左图的一个点，沿着它在右图水平极线方向寻找和它最匹配的像素点，说起来简单，但实际操作起来并不容易。
(1）实际上要保证两个相机完全共面且参数一致是非常困难的，而且在计算中会产生误差积累，因此对于左图中的一个点，其右图的对应点不一定恰好在极线上。应该是在极线附近，所以搜索范围需要适当放宽。
(2）单个像素点进行比较鲁棒性很差，很容易受到光照变化和视角不同的影响。
(3）基于滑动窗口的图像匹配
上述问题的解决办法是：使用滑动窗口。对于左图中一个像素点（左图中的红色方框中心），在右图中从左到右用一个尺寸滑动窗口内的像素和它计算相似程度，相似度的度量有很多方法，比如误差平方法，ssd。ssd越小的位置对应的像素点就是最佳匹配结果。

具体操作中还有很多实际问题，比如滑动窗口的尺寸。
基于能量优化的图像匹配
目前比较主流的方法都是基于能量优化的方法来实现匹配。能量优化通常会定义一个能量函数。比如对于两张图中像素点的匹配问题来说，我们定义的能量函数如下图公式1.
（1）在左图中所有的像素点和右图中对应的像素点越近似越好，反映在图像里就是灰度值越接近越好，也就是下图公式2的描述。
（2）在 同一张图片里，两个相邻的像素点视差（深度值）也应该相近。也就是下图公式3的描述。

$$\text{1 Energy = matchCost + smoothnessCost }$$
$$\text{2 matchCost }=\sum _{xy}\Vert I(x,y)-J\left(x+d_{xy},y\right)\Vert$$
$$\text{ 3 smoothnessCost }=\sum _{\text{neighbor pixels }p,q}\left|d_p-d_q\right|$$
上述公式1代表的能量函数就是著名的马尔科夫随机场(Markov Random Field)模型。通过对能量函数最小化，我们最后得到了一个最佳的匹配结果。有了左右图的每个像素的匹配结果，根据前面的深度计算公式就可以得到每个像素点的深度值，最终得到一幅深度图。
参考博客

3. 畸变与畸变矫正

相机拍摄的图片还存在一定的畸变，畸变包括桶形畸变和枕形畸变。
畸变模型包括径向畸变和切向畸变。
径向畸变公式（3阶）如下：
$$\begin{array}{rl}& \hat{x}=x\left(1+k_1{r}^2+k_2{r}^4+k_3{r}^6\right)\\ & \hat{y}=y\left(1+k_1{r}^2+k_2{r}^4+k_3{r}^6\right)\end{array}$$
切向畸变公式如下：
$$\begin{array}{rl}& \hat{x}=x+\left(2p_{1}y+p_2\left(r^2+2x^2\right)\right)\\ & \hat{y}=y+\left(p_1\left(r^2+2y^2\right)+2p_{2}x\right)\end{array}$$
其中， $(x,y),(\hat{x},\hat{y})$ 分别为理想的无畸变的归一化的图像坐标、畸变后的归一化图像坐标， $r$ 为图像像素点到图像中心点 的距离，即 $r^2=x^2+y^2$ 。
相机标定的第二个目的就是获得相机的畸变参数，如上式中的 $k_1,k_2,k_3,p_1,p_2$ 等，进而对拍摄的图片进行去畸变处理。

二、张正友标定法简介

张正友标定法利用如下图所示的棋盘格标定板，在得到一张标定板的图像之后，可以利用相应的图像检测算法得到每一个角点的像素坐标$(u,v)$。

张正友标定法将世界坐标系固定于棋盘格上，则棋盘格上任一点的物理坐标W = 0 ，由于标定板的世界坐标系是人为事先定义好的，标定板上每一个格子的大小是已知的，我们可以计算得到每一个角点在世界坐标系下的物理坐标( U , V , W = 0 ) 。

我们将利用这些信息：每一个角点的像素坐标$(u,v)$ 、每一个角点在世界坐标系下的物理坐标( U , V , W = 0 ) ，来进行相机的标定，获得相机的内外参矩阵、畸变参数。

三、标定相机内外参

张正友标定法标定相机的内外参数的思路如下：

1）、求解单应性矩阵Z,（矩阵Z是内参矩阵与外参矩阵的积）；

2）、求解内参矩阵；

3）、求解外参矩阵。
张氏标定算法具体流程为：首先忽略相机畸变对成像的影响并求解出单应性矩阵，并根据多个单应性矩阵得到相机的内外参数；然后考虑相机存在的畸变，即引入畸变参数，将线性模型下求解出的标定参数作为初值，通过极大似然估计算法得到优化后的标定参数，最后基于每个单目相机标定出的参数再对双目相机进行联合标定

1. 求解内参和外参的积

将世界坐标系固定于棋盘格上，则棋盘格上任一点的物理坐标W = 0 W = 0W=0。因此，原单点无畸变的成像模型可以化为下式：
$$Z\left(\begin{array}{l}u\\ v\\ 1\end{array}\right)=\left(\begin{array}{ccc}\frac{f}{dX}& -\frac{f\cot \theta }{dX}& u_0\\ 0& \frac{f}{dY\sin \theta }& v_0\\ 0& 0& 1\end{array}\right)\left(\begin{array}{lll}R1& R2& T\end{array}\right)\left(\begin{array}{c}U\\ V\\ 1\end{array}\right)=A\left(\begin{array}{ccc}R1& R2& T\end{array}\right)\left(\begin{array}{l}U\\ V\\ 1\end{array}\right)（3.1）$$
在公式(3.1)中，$Z$为一个非零的尺度因子。$A$ 为相机的内参矩阵，$R$ 为描述两个坐标系之间的旋转矩阵，同理$T$为平移向量。
通过公式(3.1)可知，标定板上任意一个角点与其对应的像素坐标都可以通过矩阵 H 建立起一种单应性关系。其中， $R1,R2$ 为旋转矩阵 $R$ 的前两列。为了简便，将内参矩阵记为 $A$ 。
对于不同的图片，内参矩阵 $A$ 为定值；对于同一张图片，内参矩阵 $A$ ，外参矩阵 $(R1R2T)$ 为定值; 对于同一张图 片上的单点，内参矩阵 $A$ ，外参矩阵 $(R1R2T)$ ，尺度因子 $Z$ 为定值。
我们将 $A\left(\begin{array}{lll}R1& R2& T\end{array}\right)$ 记为矩阵 $H，H$ 即为内参矩阵和外参矩阵的积，也叫单应性矩阵，记矩阵 $H$ 的三列为 $(H1H2H3)$ ，则 有:
$$\left(\begin{array}{l}u\\ v\\ 1\end{array}\right)=\frac{1}{Z}H\left(\begin{array}{l}U\\ V\\ 1\end{array}\right)=\frac{1}{Z}\left(\begin{array}{lll}{H}_{11}& H_{12}& H_{13}\\ H_{12}& H_{22}& H_{32}\\ H_{31}& H_{32}& H_{33}\end{array}\right)\left(\begin{array}{l}U\\ V\\ 1\end{array}\right)$$
其中：
$$\mathbf{H}=\left[\begin{array}{lll}{H}_{11}& H_{12}& H_{13}\\ H_{21}& H_{22}& H_{23}\\ H_{31}& H_{32}& 1\end{array}\right]$$

利用上式，消去尺度因子 $Z$ ，可得:
$$\begin{array}{rl}& u=\frac{H_{11}U+H_{12}V+H_{13}}{H_{31}U+H_{32}V+H_{33}}\\ & v=\frac{H_{21}U+H_{22}V+H_{23}}{H_{31}U+H_{32}V+H_{33}}\end{array}$$
由这里的 $H$ 是齐次矩阵，有8个独立末知元素。每一个标定板角点可以提供两个约束方程 $(u,U,V$ 的对应关系， $v,U,V$ 的对应关系提供了两个约束方程) 。因此，当一张图片上的标定板角点数量等于4时，即可求得该图片对应的矩阵 ${\mathrm{H}}_{\text{。 }}$ 当 一张图片上的标定板角点数量大于 4 时，利用最小二乘法回归最佳的矩阵 $H$ 。

联立为方程组的：
$$\{\begin{array}{l}uU{H}_{31}+uV{H}_{32}+u=H_{11}U+H_{12}V+H_{13}\\ vU{H}_{31}+vV{H}_{32}+v=H_{21}U+H_{22}{Y}_w+H_{23}\end{array}$$
令 $\mathbf{h}=\left[\begin{array}{llllllll}{H}_{11}& H_{12}& H_{13}& H_{21}& H_{22}& H_{23}& H_{31}& H_{32}\end{array}\right]$, 则公式(3.5) 可以改写成矩阵形式:

此时，尺度因子 $Z$ 已经被消去，因此上式对于同一张图片上所有的角点均成立。 $(u,v)$ 是像素坐标系下的标定板角点的坐 标， $(U,V)$ 是世界坐标系下的标定板角点的坐标。通过图像识别算法，我们可以得到标定板角点的像素坐标 $(u,v)$ ，又由 于标定板的世界坐标系是人为定义好的，标定板上每一个格子的大小是已知的，我们可以计算得到世界坐标系下的 $(U,V)$ 。此时，相当于像素坐标 $(u,v)$ 和世界坐标$(U,V)$已知，即可求得矩阵H。

2. 求解内参矩阵

我们已知了矩阵 $H=A\left(\begin{array}{lll}R1& R2& T\end{array}\right)$ ，接下来需要求解相机的内参矩阵 $A$ 。
我们利用 $R1,R2$ 作为旋转矩阵 $R$ 的两列，存在单位正交的关系，即:
$$\begin{array}{c}R{1}^{T}R2=0\\ R{1}^{T}R1=R{2}^{T}R2=1\end{array}$$

则由 $H$ 和 $R1,R2$ 的关系，可知:
$$\begin{array}{rl}& R1=A^{-1}H1\\ & R2=A^{-1}H2\end{array}$$
代入可得:
$$\begin{array}{c}H{1}^T{A}^{-T}{A}^{-1}H2=0\\ H{1}^T{A}^{-T}{A}^{-1}H1=H{2}^T{A}^{-T}{A}^{-1}H2=1\end{array}$$
另外，我们发现，上述两个约束方程中均存在矩阵 $A^{-T}{A}^{-1}$ 。因此，我们记 $A^{-T}{A}^{-1}=B$ ，则 $B$ 为对称阵。我们试图先 求解出矩阵 $B$ ，通过矩阵 $B$ 再求解相机的内参矩阵 $A_{\text{。 }}$
同时，为了简便，我们记相机内参矩阵 $A$ 为:
$$A=\left(\begin{array}{cccc}\frac{f}{dX}& -\frac{f\cot \theta }{dX}& u_0& 0\\ 0& \frac{f}{dY\sin \theta }& v_0& 0\\ 0& 0& 1& 0\end{array}\right)=\left[\begin{array}{ccc}\alpha & \gamma & u_0\\ 0& \beta & v_0\\ 0& 0& 1\end{array}\right]$$
则：
$$A^{-1}=\left[\begin{array}{ccc}\frac{1}{\alpha }& -\frac{\gamma }{\alpha \beta }& \frac{\gamma v_0-\beta u_0}{\alpha \beta }\\ 0& \frac{1}{\beta }& -\frac{v_0}{\beta }\\ 0& 0& 1\end{array}\right]$$
则用矩阵 $A$ 表示矩阵 $B$ 得:
$$B=A^{-T}{A}^{-1}=\left[\begin{array}{ccc}\frac{1}{{\alpha }^2}& -\frac{\gamma }{{\alpha }^2\beta }& \frac{\gamma v_0-\beta u_0}{{\alpha }^2\beta }\\ -\frac{\gamma }{{\alpha }^2\beta }& \frac{1}{{\beta }^2}+\frac{{\gamma }^2}{{\alpha }^2{\beta }^2}& \frac{\gamma \left(\beta u_0-\gamma v_0\right)}{{\alpha }^2{\beta }^2}-\frac{v_0}{{\beta }^2}\\ \frac{\gamma v_0-\beta u_0}{{\alpha }^2\beta }& \frac{\gamma \left(\beta u_0-\gamma v_0\right)}{{\alpha }^2{\beta }^2}-\frac{v_0}{{\beta }^2}& \frac{{\left(\beta u_0-\gamma v_0\right)}^2}{{\alpha }^2{\beta }^2}+\frac{v_0^2}{{\beta }^2}+1\end{array}\right]=\left[\begin{array}{ccc}{B}_{11}& B_{12}& B_{13}\\ B_{12}& B_{22}& B_{23}\\ B_{13}& B_{23}& B_{33}\end{array}\right]$$
注意: 由于 $B$ 为对称阵，上式出现了两次 $B_{12},B_{13},B_{23}$ 。
这里，我们可以使用 $B=A^{-T}{A}^{-1}$ 将前面通过 $R1,R2$ 单位正交得到的约束方程化为:
$$\begin{array}{c}H{1}^{T}BH2=0\\ H{1}^{T}BH1=H{2}^{T}BH2=1\end{array}$$
因此，为了求解矩阵 $B$ ，我们必须计算 $H_i^{T}B{H}_j$ 。则:
$$\begin{array}{rl}& H_i^{T}B{H}_j=\left[\begin{array}{lll}{H}_{1i}& H_{2i}& H_{3i}\end{array}\right]\left[\begin{array}{ccc}{B}_{11}& B_{12}& B_{13}\\ B_{12}& B_{22}& B_{23}\\ B_{13}& B_{23}& B_{33}\end{array}\right]\left[\begin{array}{c}{H}_{1j}\\ H_{2j}\\ H_{3j}\end{array}\right]\\ & =\left[\begin{array}{llllll}{H}_{1i}{H}_{1j}& H_{1i}{H}_{2j}+H_{2i}{H}_{1j}& H_{2i}{H}_{2j}& H_{1i}{H}_{3j}+H_{3i}{H}_{1j}& H_{2i}{H}_{3j}+H_{3i}{H}_{2j}& H_{3i}{H}_{3j}\end{array}\right]\left[\begin{array}{l}{B}_{11}\\ B_{12}\\ B_{13}\\ B_{22}\\ B_{23}\\ B_{33}\end{array}\right]\end{array}$$
上述方程看起来有点复杂，但是其实不然，我们可以记：
$$\begin{array}{c}{v}_{ij}={\left[\begin{array}{lcllll}{H}_{1i}{H}_{1j}& H_{1i}{H}_{2j}+H_{2i}{H}_{1j}& H_{2i}{H}_{2j}& H_{1i}{H}_{3j}+H_{3i}{H}_{1j}& H_{2i}{H}_{3j}+H_{3i}{H}_{2j}& H_{3i}{H}_{3j}\end{array}\right]}^T\\ b={\left[\begin{array}{llllll}{B}_{11}& B_{12}& B_{13}& B_{22}& B_{23}& B_{33}\end{array}\right]}^T\end{array}$$
则上述方程化为:
$$H_i^{T}B{H}_j=v_{ij}b$$
此时，通过 $R1,R2$ 单位正交得到的约束方程可化为:
$$\begin{array}{c}{v}_{12}^{T}b=0\\ v_{11}^{T}b=v_{22}^{T}b=1\end{array}$$
即:
$$\left[\begin{array}{c}{v}_{12}^T\\ v_{11}^T-v_{22}^T\end{array}\right]b=vb=0$$
其中，矩阵 $v=\left[\begin{array}{c}{v}_{12}^T\\ v_{11}^T-v_{22}^T\end{array}\right]$
由于矩阵 $H$ 已知，矩阵 $v$ 又全部由矩阵 $H$ 的元素构成，因此矩阵 $v$ 已知。
此时，我们只要求解出向量 $b$ ，即可得到矩阵 $B$ 。每张标定板图片可以提供一个 $vb=0$ 的约束关系，该约束关系含有两个 约束方程。但是，向量 $b$ 有6个末知元素。因此，单张图片提供的两个约束方程是不足以解出来向量 $b$ 。因此，我们只要取 3 张标定板昭片，得到 3 个 $vb=0$ 的约束关系，即 6 个方程，即可求解向量 $b$ 。当标定板图片的个数大于 3 时（事实上一般需 要15到20张标定板图片)，可采用最小二成拟合最佳的向量 $b$ ，并得到矩阵 $B$ 。
$$B=\left[\begin{array}{ccc}\frac{1}{{\alpha }^2}& -\frac{\gamma }{{\alpha }^2\beta }& \frac{\gamma v_0-\beta u_0}{{\alpha }^2\beta }\\ -\frac{\gamma }{{\alpha }^2\beta }& \frac{1}{{\beta }^2}+\frac{{\gamma }^2}{{\alpha }^2{\beta }^2}& \frac{\gamma \left(\beta u_0-\gamma v_0\right)}{{\alpha }^2{\beta }^2}-\frac{v_0}{{\beta }^2}\\ \frac{\gamma v_0-\beta u_0}{{\alpha }^2\beta }& \frac{\gamma \left(\beta u_0-\gamma v_0\right)}{{\alpha }^2{\beta }^2}-\frac{v_0}{{\beta }^2}& \frac{{\left(\beta u_0-\gamma v_0\right)}^2}{{\alpha }^2{\beta }^2}+\frac{v_0^2}{{\beta }^2}+1\end{array}\right]=\left[\begin{array}{ccc}{B}_{11}& B_{12}& B_{13}\\ B_{12}& B_{22}& B_{23}\\ B_{13}& B_{23}& B_{33}\end{array}\right]$$
根据矩阵 $B$ 的元素和相机内参 $\alpha ,\beta ,\gamma ,u_0,v_0$ 的对应关系（如上式），可得到:
$$\begin{array}{c}{v}_0=\frac{B_{12}{B}_{13}-B_{11}{B}_{23}}{B_{11}{B}_{22}-B_{12}^2}\\ \alpha =\sqrt{\frac{1}{B_{11}}}\\ \beta =\sqrt{\frac{B_{11}}{B_{11}{B}_{22}-B_{12}^2}}\\ \gamma =-B_{12}{\alpha }^2\beta \\ u_0=\frac{\gamma v_0}{\beta }-B_{13}{\alpha }^2\end{array}$$
即可求得相机的内参矩阵 $A=\left(\begin{array}{cccc}\frac{f}{dX}& -\frac{f\cot \theta }{dX}& u_0& 0\\ 0& \frac{f}{dY\sin \theta }& v_0& 0\\ 0& 0& 1& 0\end{array}\right)=\left[\begin{array}{ccc}\alpha & \gamma & u_0\\ 0& \beta & v_0\\ 0& 0& 1\end{array}\right]$

3. 求解外参矩阵

根据公式$\left[\begin{array}{lll}{\mathbf{H}}_1& {\mathbf{H}}_2& {\mathbf{H}}_3\end{array}\right]=ZA\left[\begin{array}{lll}{\mathbf{R}}_1& {\mathbf{R}}_2& T\end{array}\right]$可得外参数的解为:
$$\{\begin{array}{l}{\mathbf{R}}_1=\frac{{\mathbf{H}}_1{A}^{-1}}{z}\\ {\mathbf{R}}_2=\frac{{\mathbf{H}}_2{A}^{-1}}{z}\\ {\mathbf{R}}_3={\mathbf{R}}_1\times {\mathbf{R}}_2\\ \mathbf{T}=\frac{{\mathbf{H}}_3{A}^{-1}}{z}\end{array}$$
这里再次强调一下，对于同一个相机，相机的内参矩阵取决于相机的内部参数，无论标定板和相机的位置关系是怎么样的，相机的内参矩阵不变。这也正是在第2部分“求解内参矩阵”中，我们可以利用不同的图片（标定板和相机位置关系不同）获取的矩阵H HH，共同求解相机内参矩阵A AA的原因。

但是，外参矩阵反映的是标定板和相机的位置关系。对于不同的图片，标定板和相机的位置关系已经改变，此时每一张图片对应的外参矩阵都是不同的。
在关系: $A(R1R2T)=H$ 中，我们已经求解得到了矩阵 $H$ (对于同一张图片相同，对于不同的图片不同) 、矩 阵 $A$ (对于不同的图片都相同) 。通过公式: ( $(R1R2T)=A^{-1}H$ ，即可求得每一张图片对应的外参矩阵 $\left(\begin{array}{lll}R1& R2& T\end{array}\right)$ 。

注意，这里值得指出，完整的外参矩阵为 $\left(\begin{array}{cc}R& T\\ 0& 1\end{array}\right)$ 。但是，由于张正友标定板将世界坐标系的原点选取在棋盘格上，则 棋盘格上任一点的物理坐标 $W=0$ ，将旋转矩阵的 $R$ 的第三列 $R3$ 消掉。因此， $R3$ 在坐标转化中并没有作用。但是 $R3$ 要 使得 $R$ 满足旋转矩阵的性质，即列与列之间单位正交。因此可以通过向量 $R1,R2$ 的叉乘，即 $R3=R1\times R2$ ，计算得到 $R3$ 。
向量的叉乘，即求同时垂直两个向量的向量，即c垂直于a，同时c垂直于b（a与c的夹角为90°，b与c的夹角为90°）
此时，相机的内参矩阵和外参矩阵均已得到。

注：以上推导都是假设不存在畸变参数的情况下成立的。但是事实上，相机是存在畸变参数的，因此张正友标定法还需要通过L-M算法对于参数进行迭代优化。

更多详细内容见：相机标定—— 张正友标定法（2）