人工智能与深度学习概念(3)——目标分类-CNN
转载请注明作者和出处:https://blog.csdn.net/qq_28810395
Python版本: Python3.x
运行平台: Windows 10
IDE: Pycharm profession 2019
一、目标分类简介
在现在的计算机视觉(computer vision,CV)中,图像分类、目标检测、图像分割是计算机视觉领域额三个主要任务。从图像中解析出可供计算机理解的信息,是计算机视觉邻域重点要解决的问题,深度学习模型的出现,其强大的表示能力为机器视觉提供了巨大的助力。下图就是机器理解图像的三个层次。

- 目标分类(Classification):
将图像结构化为某一类别的信息,用事先确定好的类别(category)或实例ID来描述图片。这一任务是最简单、最基础的图像理解任务,也是深度学习模型最先取得突破和实现大规模应用的任务。其中,ImageNet是最权威的评测集,每年的ILSVRC催生了大量的优秀深度网络结构,为其他任务提供了基础。在应用领域,人脸、场景的识别等都可以归为分类任务。
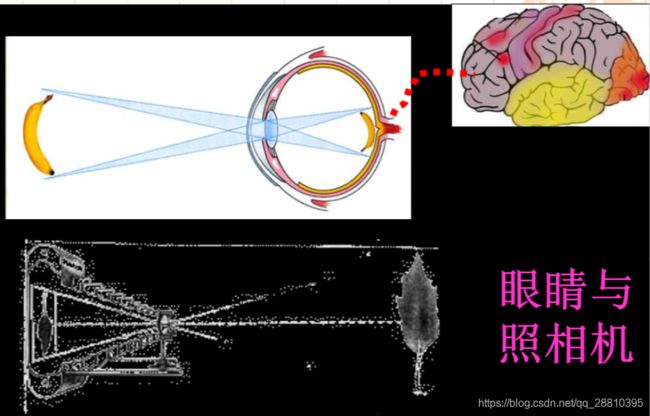
二、生物视觉原理
-
生物层面的视觉图像处理流程:
1、像素信号瞳孔摄入,视网膜感光细胞传导刺激反应
2、大脑皮层细胞处理,感知差异构成的边缘和方向
3、神经细胞处理,提炼形状颜色等特征
4、大脑进一步抽象,获得认知
5、与记忆进行匹配,得到判断 -
机器模拟生物识别,其处理流程为:
1、接受图像数据
2、获取图像特征
3、根据特征获得类别信息
4、输出目标类别
图像通道
模拟眼镜视网膜的感色原理,我们所观察的色彩都是RGB三原色组成,所以一个彩色图片便可有RGB三色的灰度图叠加而成,而每个灰度图片也是一个个的像素拼凑而成(如同马赛克),在计算机处理中,计算机存储的图像数据便是这RGB灰度图像的矩阵数据。
三、机器视觉的特征表达
对于图片进行检测分类,肯定要根据所识别的物理的特征进行区分,对于一个物体,特征描述的越清晰,识别效果肯定越准确。比如西瓜好坏的识别,从瓜藤识别、瓜蒂识别、颜色识别再到花纹识别。特征逐渐添加,识别的就越准确。
在计算机中利用向量进行标识特征,利用神经网络逐层卷积,随着卷积的逐步深入,特征会逐渐变得抽象,特征转向各类细节都会被高维特征图各通道的激活单元代表,形成多维向量。
三层卷积后图片已经变得抽象

四、卷积
数学定义
在高数课本中,对与卷积表达式离散定义如下所示:

进行矩阵表达的数学定义式:
![]()
进入卷积神经网络,函数定义式为下图,其中X为输入,W为卷积核。如果X是二维输入,那么W也是二维矩阵,如果X是多维张量,那么W也是多维张量。

CNN卷积理解
从函数(或者说映射、变换)的角度理解。 卷积过程是在图像每个位置进行线性变换映射成新值的过程,将卷积核看成权重,若拉成向量记为w,图像对应位置的像素拉成向量记为x,则该位置卷积结果为y=w′x+b,即向量内积+偏置,将x变换为y。从这个角度看,多层卷积是在进行逐层映射,整体构成一个复杂函数,训练过程是在学习每个局部映射所需的权重,训练过程可以看成是函数拟合的过程。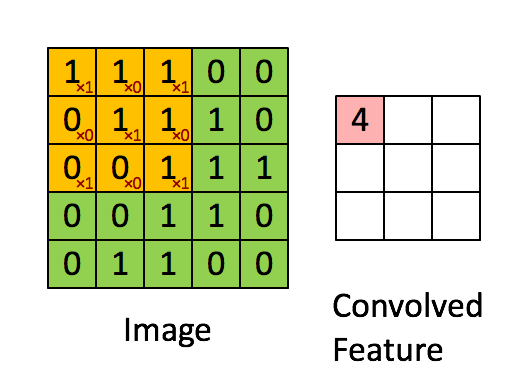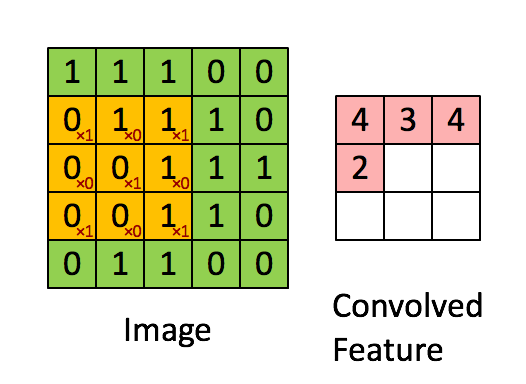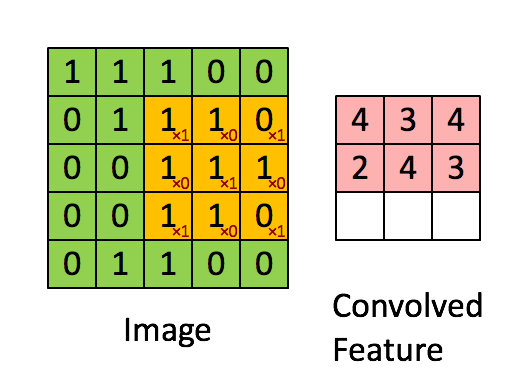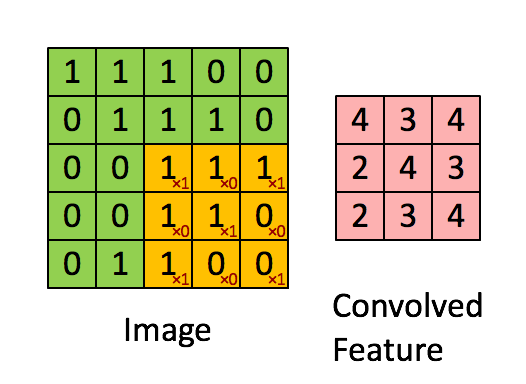
如图是对一张图进行卷积遍历的过程,上图的3×3的方格是二维的卷积核。执行矩阵点成运算,其中的数字即卷积核的参数,参数的原始图像对应像素值进行相乘求和,获得新值,进行对图片特征的提取和压缩。
感受野
应对不同特征图的设计,在进行卷积过程中,补零(padding)和步长(stride)可以控制特征图的尺寸。

如图虚线框就是我们人工进行补零操作,卷积核每次移动的距离就是步长,在这副图中,补零为2,步长为1可以将特征图进行放大,不影响特征特点。

补零为1,步长为1,特征图大小不变,特征信息无影响。

补零为1,步长为2,特征图缩小。
五、全连接层与输出层
-
全连接层
全连接层的每一个结点斗鱼上一层的所有结点相连,用来把前边提取到的特征综合起来。由于其全相连的特性,一般全连接层的参数也是最多的。其作用就是高度整合特征,方便交给最后的分类器或者回归,其坏处在于会破坏图像的空间结构,且参数太多。现在的主流趋势是尽量避免使用全连接层。 -
输出层
输出层通常连接全连接层,因此其结构和工作原理与传统前馈神经网络中的输出层相同。对于图像分类问题,输出层使用逻辑函数或归一化指数函数(softmax function)输出分类标签。
AlexNet
AlexNet共8层,由5个卷积层和3个全连接层组成,输出是1000维的向量。

AlexNet接受的图像是227×227×3,长宽为227,RGB三通道的图片。
- 第一层:卷积核大小是11×11,步长为4 ,通道数为96进行卷积(CONV),形成55×55×96的特征矩阵图。紧接着是一个线性修正单元(ReLU)激活函数(下文) ,再接着局部正则化(LRN)(下文),最后是一个卷积核大小为3×3 ,步长为2 的最大池化层(POOL)(下文),形成27×27×96的特征矩阵。
- 第二层: 卷积核大小是5×5 步长是1 通道数为256 紧接着是一个ReLU激活函数、局部正则化 最后是一个卷积核大小为3×3,步长为2 的最大池化层。
- 第三层: 卷积核大小为 3×3, 步长为 1,通道数分别是384,没有做LRN和Pool。
- 第四层: 卷积核大小为 3×3, 步长为 1,通道数分别是384,没有做LRN和Pool。
- 第五层: 卷积核大小为 3×3, 步长为 1,通道数分别是384,进行最大池化,步长为2.
- 第六、七、八层:这三层是全连接层每一层的神经元的个数为4096,最终输出softmax为1000,因为上面介绍过,ImageNet这个比赛的分类个数为1000。全连接层中使用了RELU和Dropout。

详细理解可以查看详解
Alexnet的Tensorflow实现代码
# -*- coding=UTF-8 -*-
import tensorflow as tf
# 输入数据
import input_data
mnist = input_data.read_data_sets("/tmp/data/", one_hot=True)
# 定义网络超参数
learning_rate = 0.001
training_iters = 200000
batch_size = 64
display_step = 20
# 定义网络参数
n_input = 784 # 输入的维度
n_classes = 10 # 标签的维度
dropout = 0.8 # Dropout 的概率
# 占位符输入
x = tf.placeholder(tf.types.float32, [None, n_input])
y = tf.placeholder(tf.types.float32, [None, n_classes])
keep_prob = tf.placeholder(tf.types.float32)
# 卷积操作
def conv2d(name, l_input, w, b):
return tf.nn.relu(tf.nn.bias_add( \
tf.nn.conv2d(l_input, w, strides=[1, 1, 1, 1], padding='SAME'),b) \
, name=name)
# 最大下采样操作
def max_pool(name, l_input, k):
return tf.nn.max_pool(l_input, ksize=[1, k, k, 1], \
strides=[1, k, k, 1], padding='SAME', name=name)
# 归一化操作
def norm(name, l_input, lsize=4):
return tf.nn.lrn(l_input, lsize, bias=1.0, alpha=0.001 / 9.0, beta=0.75, name=name)
# 定义整个网络
def alex_net(_X, _weights, _biases, _dropout):
_X = tf.reshape(_X, shape=[-1, 28, 28, 1]) # 向量转为矩阵
# 卷积层
conv1 = conv2d('conv1', _X, _weights['wc1'], _biases['bc1'])
# 下采样层
pool1 = max_pool('pool1', conv1, k=2)
# 归一化层
norm1 = norm('norm1', pool1, lsize=4)
# Dropout
norm1 = tf.nn.dropout(norm1, _dropout)
# 卷积
conv2 = conv2d('conv2', norm1, _weights['wc2'], _biases['bc2'])
# 下采样
pool2 = max_pool('pool2', conv2, k=2)
# 归一化
norm2 = norm('norm2', pool2, lsize=4)
# Dropout
norm2 = tf.nn.dropout(norm2, _dropout)
# 卷积
conv3 = conv2d('conv3', norm2, _weights['wc3'], _biases['bc3'])
# 下采样
pool3 = max_pool('pool3', conv3, k=2)
# 归一化
norm3 = norm('norm3', pool3, lsize=4)
# Dropout
norm3 = tf.nn.dropout(norm3, _dropout)
# 全连接层,先把特征图转为向量
dense1 = tf.reshape(norm3, [-1, _weights['wd1'].get_shape().as_list()[0]])
dense1 = tf.nn.relu(tf.matmul(dense1, _weights['wd1']) + _biases['bd1'], name='fc1')
# 全连接层
dense2 = tf.nn.relu(tf.matmul(dense1, _weights['wd2']) + _biases['bd2'], name='fc2')
# Relu activation
# 网络输出层
out = tf.matmul(dense2, _weights['out']) + _biases['out']
return out
# 存储所有的网络参数
weights = {
'wc1': tf.Variable(tf.random_normal([3, 3, 1, 64])),
'wc2': tf.Variable(tf.random_normal([3, 3, 64, 128])),
'wc3': tf.Variable(tf.random_normal([3, 3, 128, 256])),
'wd1': tf.Variable(tf.random_normal([4*4*256, 1024])),
'wd2': tf.Variable(tf.random_normal([1024, 1024])),
'out': tf.Variable(tf.random_normal([1024, 10]))
}
biases = {
'bc1': tf.Variable(tf.random_normal([64])),
'bc2': tf.Variable(tf.random_normal([128])),
'bc3': tf.Variable(tf.random_normal([256])),
'bd1': tf.Variable(tf.random_normal([1024])),
'bd2': tf.Variable(tf.random_normal([1024])),
'out': tf.Variable(tf.random_normal([n_classes]))
}
# 构建模型
pred = alex_net(x, weights, biases, keep_prob)
# 定义损失函数和学习步骤
cost = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(pred, y))
optimizer = tf.train.AdamOptimizer(learning_rate=learning_rate).minimize(cost)
# 测试网络
correct_pred = tf.equal(tf.argmax(pred,1), tf.argmax(y,1))
accuracy = tf.reduce_mean(tf.cast(correct_pred, tf.float32))
# 初始化所有的共享变量
init = tf.initialize_all_variables()
# 开启一个训练
with tf.Session() as sess:
sess.run(init)
step = 1
# Keep training until reach max iterations
while step * batch_size < training_iters:
batch_xs, batch_ys = mnist.train.next_batch(batch_size)
# 获取批数据
sess.run(optimizer, feed_dict={x: batch_xs, y: batch_ys, keep_prob: dropout})
if step % display_step == 0:
# 计算精度
acc = sess.run(accuracy, feed_dict={x: batch_xs, y: batch_ys, keep_prob: 1.})
# 计算损失值
loss = sess.run(cost, feed_dict={x: batch_xs, y: batch_ys, keep_prob: 1.})
print "Iter " + str(step*batch_size) + ", Minibatch Loss= " + "{:.6f}".format(loss) + ", Training Accuracy= " + "{:.5f}".format(acc)
step += 1
print "Optimization Finished!"
# 计算测试精度
print "Testing Accuracy:", sess.run(accuracy, feed_dict={x: mnist.test.images[:256], y: mnist.test.labels[:256], keep_prob: 1.})
#以上代码忽略了部分卷积层,全连接层使用了特定的权重。
六、池化
池化(Pooling)是卷积神经网络中另一个重要的概念。有多种不同形式的非线性池化尺寸的传统池化滑窗,这种重叠特性有效地降低了错误率。层类似,只是计算最大池层的相邻窗口彼此重叠。有效地避免了特征信息的遗失,相比于同等尺寸的传统池化滑窗,这种重叠特性有效地降低了错误率。
池化简单来说就是选举,选一个单位代替整个单位,选一个像素值代替一个区域的像素值。最大池化就是挑一个最大的值来代替。
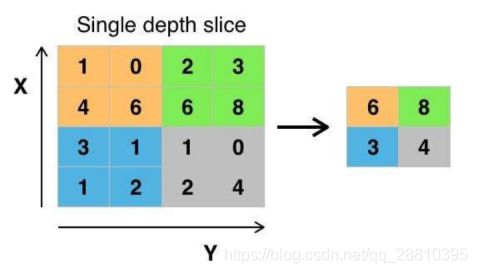
池化作用就是对特征图数据行压缩,且具有改变特征图尺寸的作用。
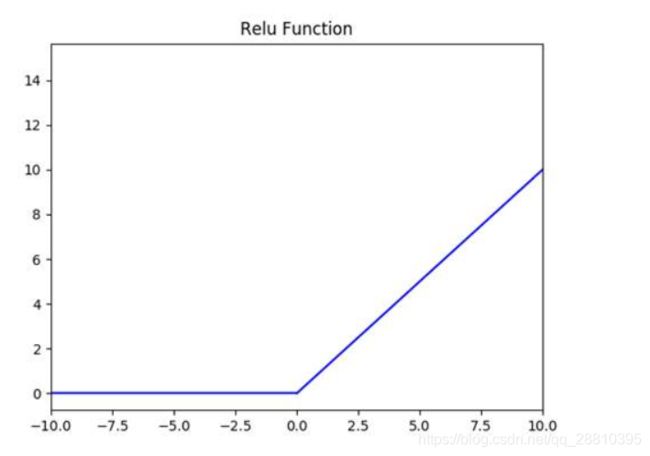
七、线性修正单元(ReLU)
线性修正单元(Rectified Linear Units,ReLU)作为激活函数存在(Activation function)。它可以增强函数和整个神经网络的非线性特性,而并不改变卷积层的结果。通过AlexNet的实践表明,使用ReLU非线性函数,训练深度CNN时比使用tanh或sigmoid等饱和激活函数要快得多。
八、局部归一化(LRN)
即Local Response Normalization,归一化有助于加快收敛速度,并对局部神经元的活动建立竞争机制,使得其中响应比较大的值变得相对更大,并抑制其他反馈较小的神经元,使得模型调用的计算资源更加集中在少量的特定特征上,增强了模型的泛化能力。经过局部响应归一化,Top1和Top5错误率分别降低1.4%和1.2%。
九、过拟合
神经网络的学习能力与其大小有关,但是如果训练设置不当的话,模型会在不理解概念的情况下过度记住训练数据的特征。神经网络能够很好地处理训练数据,但却不能很好地学习真正的概念,无法处理新的未见过的测试数据。这就是过拟合。
常见的解决过拟合办法:
- 数据增强
- 正则化
- 提前停止
- 节点随机丢弃
1.提前停止(Early stopping)
&emsp提前停止,每个epoch后dd偶计算在验证集上的分类准确率,一旦分类准确率饱和,就停止训练。
2.节点随机丢弃(DROPOUT)
节点丢弃,在训练中的每次传播时随机选择神经层中的一些节点并将其临时隐藏。在下一次循环中再隐藏另一些神经元,如此直至训练结束。在AlexNet最后2个全连接层中使用了Dropout,因为全连接层容易过拟合,而卷积层不容易过拟合。
- 相对于训练大量模型耗费大量时间,dropout在AlexNet中只需花费2倍的训练时间。
- 引入稀疏性。因为部分神经元被删除,原来有些特征可能会依赖于固定关系的隐含节点的共同作用,通过Dropout的话,就有效地阻止了某些特征在其他特征存在下才有效果的情况。
- 类似模型集成。在Dropout训练过程中,网络因为随机删除节点,导致实际上存在多种网络结构,却共用一组参数。
十、参考文献
图片来源于网络
- https://blog.csdn.net/qq_41776781/article/details/94437671
- http://edu.cstor.cn/#
- https://blog.csdn.net/luoluonuoyasuolong/article/details/81750190
- https://baike.baidu.com/item/AlexNet/22689612?fr=aladdin
- https://www.cnblogs.com/xiaoboge/p/10544336.html
- https://www.cnblogs.com/mimandehuanxue/p/8994427.html


