数据的存储

---

1. 数据类型介绍

C 语言类型分为两类：

• 内置类型 (C语言本身具有的类型)
• 自定义类型（构造类型）

前面学习的基本的 内置类型 ：

char        //字符数据类型
short       //短整型
int         //整形
long        //长整型
long long   //更长的整形 -- 在早期（比如vc6.0）编译器不支持
float       //单精度浮点数
double      //双精度浮点数
//C语言没有字符串类型。

类型的意义：

• 使用这个类型开辟内存空间的大小（大小决定了使用范围）。
• 如何看待内存空间的视角。

2. 类型的基本归类

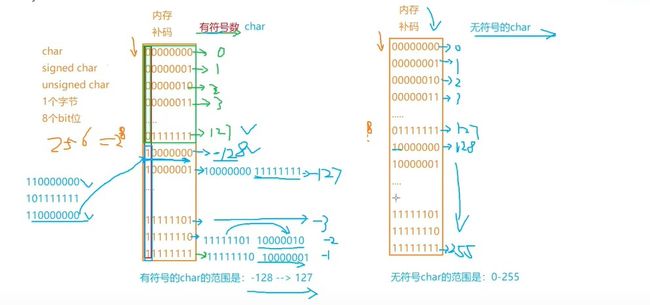
整型家族 – 默认都是有符号的。

char
    unsigned char    11111111   -- 255
    signed char                 -128 ~ 127  
short
    unsigned short [int]   -- int 可以省略
    signed short [int]
int 
    unsigned int
    signed int
long
    unsigned long [int]
    signed long [int]

#include 
int main()
{
    char a; // 有符号？还是无符号？
    // 取决于编译器，大部分编译器下char 是 signed char
    
    // short int long -- 都是有符号的
    // short == signed short
    // int == signed int
    // long == signed long
    
	unsigned char c1 = 255;
	printf("%d\n", c1); // 255
	
	char c2 = 255;
	printf("%d\n", c2); // -1

}

浮点数家族

float
double

构造类型

> 数组类型           int [10] != int [5] != char [5]
> 结构体类型 struct
> 枚举类型 enum
> 联合类型 union

指针类型

int* pi;
char* pc;
float* pf;
void* pv;     -- 无具体类型的指针

空类型

void 表示空类型（无类型）

通常应用于函数的返回类型、函数的参数、指针类型。

3. 整型在内存中的存储

之前学过一个变量的创建是要在内存中开辟空间的。空间的大小是根据不同的类型而决定的。

那接下来学习数据在所开辟内存中到底是如何存储的。

比如：

int a = 20;
int b = -10;

计算机为a 分配四个字节的空间。

那如何存储？

让我们来了解下面的概念：

3.1 原码、反码、补码

计算机中的有符号数（整型）（分为正数和负数）有三种表示方法，即原码、反码和补码。

三种表示方法均有 符号位 和 数值位 两部分，符号位都是用 0 表示 “正”，用 1 表示 “负”，而数值位 负整数的三种表示方法各不相同。

无符号数 / 正整数： 原码、反码、补码相同。

原码

直接将数字按照正负数的形式翻译成二进制就可以。

反码

将原码的符号位不变，其他位依次按位取反就可以得到了。

补码

反码+1就得到补码。

正数的原、反、补码都相同。

对于整型来说：数据存放内存中其实存放的是补码。

为什么呢？

在计算机系统中，数值（整数）一律用补码来表示和存储。原因在于，使用补码，可以将符号位和数值域统一处理；

同时，加法和减法也可以统一处理（CPU只有加法器）此外，补码与原码相互转换，其运算过程是相同的，不需要额外的硬件电路。

数据在内存中的存储：

int main()
{
	int a = 20; // 4个字节 -- 32bit
	// 00000000000000000000000000010100  -- 原码
	// 00000000000000000000000000010100  -- 反码
	// 00000000000000000000000000010100  -- 补码
    // 0x00000014
	int b = -10;
	// 10000000000000000000000000001010  -- 原码
	// 11111111111111111111111111110101  -- 反码
	// 11111111111111111111111111110110  -- 补码
    // 0xfffffff6
	return 0;
}

可以看出对于 a和b分别存储的是补码。但是我们发现顺序有点 不对劲。这是为什么呢？

3.2 大小端介绍

什么大端小端：

大端（字节序存储）模式，是指数据的低位字节内容保存在内存的高地址中，而数据的高位字节内容，保存在内存的低地址中；

小端（字节序存储）模式，是指数据的低位字节内容保存在内存的低地址中，而数据的高位字节内容，保存在内存的高地址中。

为什么有大端和小端：

为什么会有大小端模式之分呢？这是因为在计算机系统中，我们是以字节为单位的，每个地址单元都对应着一 个字节，一个字节为8bit。但是在C语言中除了8bit的char之外，还有16bit的short型，32bit的long型（要看具体的编译器），另外，对于位数大于8位的处理器，例如16位或者32位的处理器，由于寄存器宽度大于一个字节，那么必然存在着一个如何将多个字节安排的问题。因此就导致了大端存储模式和小端存储模式。

例如一个 16bit 的 short 型 x ，在内存中的地址为 0x0010 ， x 的值为 0x1122 ，那么 0x11 为高字节， 0x22 为低字节。对于大端模式，就将 0x11 放在低地址中，即 0x0010 中， 0x22 放在高地址中，即 0x0011 中。小端模式，刚好相反。我们常用的 X86 结构是小端模式，而 KEIL C51 则为大端模式。很多的ARM，DSP都为小 端模式。有些ARM处理器还可以由硬件来选择是大端模式还是小端模式。

百度2015年系统工程师笔试题：

请简述大端字节序和小端字节序的概念，设计一个小程序来判断当前机器的字节序。

// 方法1
int check_sys()
{
	int a = 1;
	// 0x 00000001
	// char* p = (char*)&a; // char* p = &a;  -- 会报警告 -- “初始化”：从“int"到“char *”的类型不兼容。
    // 返回1，小端
	// 返回0，大端
	return *(char*)&a;
}
int main()
{
	// 返回1，小端
	// 返回0，大端
	int ret = check_sys();
	if (ret == 1)
	{
		printf("小端存储\n");
	}
	else
	{
		printf("大端存储\n");
	}
	return 0;
}


// 代码2
int check_sys()
{
    union
    {
        int i;
        char c;
    }un;
    un.i = 1;
    return un.c;
}

3.3 练习

**练习1 **

//输出什么？
#include 
int main()
{
    char a= -1;
    // 10000000000000000000000000000001
    // 11111111111111111111111111111110
    // 11111111111111111111111111111111  -- 整型提升
    // 11111111  -- 赋值给 char a
    // 11111111111111111111111111111111  -- 打印时候整型提升 - 补码
    // 10000000000000000000000000000001  -- 打印原码
    signed char b=-1;
    // 11111111
    unsigned char c=-1;
    // 11111111
    // 00000000000000000000000011111111  -- 打印时，整型提升
    
    // %d - 以有符号整型的形式进行打印
    printf("a=%d,b=%d,c=%d",a,b,c);
    return 0;
}

// 运行结果
// a=-1,b=-1,c=255

练习2

#include 
int main()
{
        char a = -128;
    // 10000000000000000000000010000000
    // 11111111111111111111111101111111
    // 11111111111111111111111110000000  -- 补码
    // 10000000
    // 11111111111111111111111110000000  -- 整型提升  -- 补码  -- 无符号数 -- 也是原码
    printf("%u\n", a); // 打印十进制无符号数字
    return 0;
}

// 运行结果
// 4294967168

练习3

#include 
int main()
{
    char a = 128;
    printf("%u\n",a);
    return 0;
}

// 运行结果
// 4294967168
// 与练习2相同

练习4

int main()
{ 
	int i = -20;
	// 10000000000000000000000000010100
	// 11111111111111111111111111101011
	// 11111111111111111111111111101100 -- 补码
	unsigned int j = 10;
	// 00000000000000000000000000001010
	// 11111111111111111111111111110110  -- 和的补码
	// 11111111111111111111111111110101
	// 10000000000000000000000000001010
	printf("%d\n", i + j);// -10
	return 0;
}

练习5

#include 
int main()
{
	unsigned int i;
	for (i = 9; i >= 0; i--)
	{
		printf("%u\n", i);
		Sleep(500);
	}

	return 0;
}


// 运行结果
// 9 8 7 6 5 4 3 2 1 0 死循环

练习6

int main()
{
    char a[1000];
    int i;
    for (i = 0; i < 1000; i++)
    {
        a[i] = -1 - i;
    }
    printf("%d", strlen(a));
    return 0;
}



// 运行结果
// 255
// 分析
// a[i] =  -1 -2 -3 …… -128 127 …… 3 2 1 0 -1 …… 
// 0是字符串结束的标志，所以字符串长度为 255

练习7

#include 
unsigned char i = 0;
int main()
{
    for(i = 0;i<=255;i++)
   {
        printf("hello world\n");
   }
    return 0;
}

// 运行结果
// 死循环
// 255 + 1 = 0

4. 浮点型在内存中的存储

常见的浮点数：

3.14159 ， 1E10

浮点数家族包括：float、double、long double类型。

浮点数表示的范围：float.h中定义。

查看 INT_MAX、INT_MIN等的方法：

1. 敲除代码：

   #include 
   // limits.h 定义整型家族的限制
   // float.h 定义浮点型家族的限制
   INT_MAX
   

2. 按住ctrl+鼠标左击INT_MAX;

3. 就会跳转到他们的定义进行查看

4. 如图所示：

   

浮点数存储的例子：

int main()
{
	int n = 9;
	float* pFloat = (float*)&n;
	printf("n的值为：%d\n", n);
	printf("*pFloat的值为：%f\n", *pFloat);

	*pFloat = 9.0;
	printf("num的值为：%d\n", n); 
	printf("*pFloat的值为：%f\n", *pFloat);
	return 0;
}

运行结果：

num和 *pFloat 在内存中明明是同一个数，为什么浮点数和整数的解读结果会差别这么大？要理解这个结果，一定要搞懂懂浮点数在计算机内部的表示方法。

详细解读：

根据国际标准IEEE（电气和电子工程协会） 754，任意一个二进制浮点数 V 可以表示成下面的形式：

• (-1)^S * M * 2^E
• (-1)^s表示符号位，当s=0，V为正数；当s=1，V为负数。
• M表示有效数字，大于等于1，小于2。
• 2^E表示指数位

举例来说：十进制的9.0，写成二进制是1001.0，相当于(-1)⁰ * 1.001 * 2³。那么，按照上面 V 的格式，可以得出 S = 0，M = 1.001，E = 3。

IEEE 754 规定：

• 对于32位的浮点数，最高的 1 位是符号位 S ，接着的 8 位是指数 E，剩下的 23 位为有效数字 M。

• 对于64位的浮点数，最高的 1 位是符号位 S ，接着的11位是指数 E，剩下的52位为有效数字 M。

**IEEE 754对有效数字M和指数E，还有一些特别规定。**前面说过， 1≤M<2 ，也就是说，M可以写成 1.xxxxxx 的形式，其中xxxxxx表示小数部分。

IEEE 754规定，在计算机内部保存M时，默认这个数的第一位总是1，因此可以被舍去，只保存后面的xxxxxx部分。 比如保存1.01的时候，只保存01，等到读取的时候，再把第一位的1加上去。这样做的目的，是节省1位有效数字。 以32位浮点数为例，留给M只有23位，将第一位的1舍去以后，等于可以保存24位有效数字。

至于指数E，情况就比较复杂。

**首先，E为一个无符号整数（unsigned int）**这意味着，如果E为8位，它的取值范围为0~255；如果E为11位，它的 取值范围为0~2047。但是，我们知道，科学计数法中的E是可以出现负数的，所以IEEE 754规定，存入内存时E的真 实值必须再加上一个中间数，对于8位的E，这个中间数是127；对于11位的E，这个中间数是1023。比如，2¹⁰的E 是10，所以保存成32位浮点数时，必须保存成10+127=137，即10001001。

然后，指数E从内存中取出还可以再分成三种情况：

E不全为0或不全为1

这时，浮点数就采用下面的规则表示，即指数E的计算值减去127（或1023），得到真实值，再将有效数字M前加上第一位的1。 比如： 0.5（1/2）的二进制形式为0.1，由于规定正数部分必须为1，即将小数点右移1位， 则为1.0*2^(-1)，其阶码为-1+127=126，表示为01111110，而尾数1.0去掉整数部分为0，补齐0到23位 00000000000000000000000，则其二进制表示形式为:

0 01111110 00000000000000000000000

E全为0

这时，浮点数的指数E等于1-127（或者1-1023）即为真实值， 有效数字M不再加上第一位的1，而是还原为 0.xxxxxx的小数。这样做是为了表示±0，以及接近于0的很小的数字。

E全为1

这时，如果有效数字M全为0，表示±无穷大（正负取决于符号位s）；

解释前面的题目：

下面，让我们回到一开始的问题：为什么 0x00000009 还原成浮点数，就成了 0.000000 ？ 首先，将 0x00000009 拆 分，得到第一位符号位s=0，后面8位的指数 E=00000000 ，最后23位的有效数字M=000 0000 0000 0000 0000 1001。

9 -> 0000 0000 0000 0000 0000 0000 0000 1001

由于指数E全为0，所以符合上一节的第二种情况。

因此，浮点数V就写成：V=(-1)^0^ × 0.00000000000000000001001×2^-126^ = 1.001×2^-146^。

显然，V是一个很小的接近于0的正数，所以用十进制小 数表示就是0.000000。

再看例题的第二部分。 请问浮点数9.0，如何用二进制表示？还原成十进制又是多少？ 首先，浮点数9.0等于二进制 的1001.0，即1.001×2^3。

9.0 -> 1001.0 ->(-1)^01.0012^3 -> s=0, M=1.001,E=3+127=130

那么，第一位的符号位s=0，有效数字M等于001后面再加20个0，凑满23位，指数E等于3+127=130，即 10000010。 所以，写成二进制形式，应该是s+E+M，即

0 10000010 001 0000 0000 0000 0000 0000

这个32位的二进制数，还原成十进制，正是 1091567616 。

0000 0000 0000 0000 0000 0000 0000 1001

由于指数E全为0，所以符合上一节的第二种情况。

因此，浮点数V就写成：` V=(-1)^0^ × 0.00000000000000000001001×2^-126^ = 1.001×2^-146^`。

显然，V是一个很小的接近于0的正数，所以用十进制小 数表示就是0.000000。

再看例题的第二部分。 请问浮点数9.0，如何用二进制表示？还原成十进制又是多少？ 首先，浮点数9.0等于二进制 的1001.0，即1.001×2^3。

```c
9.0 -> 1001.0 ->(-1)^01.0012^3 -> s=0, M=1.001,E=3+127=130

那么，第一位的符号位s=0，有效数字M等于001后面再加20个0，凑满23位，指数E等于3+127=130，即 10000010。 所以，写成二进制形式，应该是s+E+M，即

0 10000010 001 0000 0000 0000 0000 0000

这个32位的二进制数，还原成十进制，正是 1091567616 。

希望可以对大家有所帮助，如果有什么不对的地方，还烦请指教，谢谢！