图文详解图的表示及DFS和BFS
图
- 图的存储结构
-
- 邻接矩阵
- 建立无向网图的邻接矩阵
- 邻接表
- 创建无向图的邻接表
- 深度优先搜索DFS
-
- 邻接矩阵的深度优先搜索
- 邻接表的深度优先搜索
- 广度优先搜索BFS
-
- 邻接矩阵的广度优先搜索
- 邻接表的广度优先搜索
- 总结
图的存储结构
邻接矩阵
邻接矩阵是表示顶点之间相邻关系的矩阵,设G(V,E)是具有n个顶点的图,则G的邻接矩阵是具有如下性质的n阶方阵:

#define MAXVEX 100
#define INFINITY 65535
//邻接矩阵
typedef struct
{
char vexs[MAXVEX];//顶点表
int arc[MAXVEX][MAXVEX];//邻接矩阵
int numVerTexes,numEdges;//图的当前点数和边数
}MGraph;
建立无向网图的邻接矩阵
void CreateMGraph(MGraph *G)
{
int x,y,w;
cout<<"输入顶点数和边数:"<<endl;
cin>>G->numVerTexes>>G->numEdges;
for (int i = 0; i < G->numVerTexes; i++)
{
cin>>G->vexs[i];
}
for (int i = 0; i < G->numVerTexes; i++)
{
for (int j = 0; j < G->numVerTexes; j++)
{
G->arc[i][j]=INFINITY;
}
}//对邻接矩阵进行初始化
for (int k = 0; k < G->numEdges; k++)
{
cout<<"输入边的下标以及权值:"<<endl;
cin>>x>>y>>w;
G->arc[x][y]=w;
G->arc[y][x]=G->arc[x][y];//无向网图的邻接矩阵是对称的
}
}
将函数稍作修改即可创建无向图、有向图和有向网图。
邻接矩阵优点:
①便于判断两个顶点之间是否有边。
②便于有向图判断各顶点出度入度,无向图判断各顶点的度。
缺点:
①不便于增加和删除顶点。
②需要扫描整个邻接矩阵才能统计完毕边的数目。
③空间复杂度大,不适合存储稀疏图。
下面我们介绍将邻接矩阵的n行改成n个单链表,适合表示稀疏图。
邻接表
typedef struct EdgeNode
{
int adjvex;
int weight;
EdgeNode *next;//指向下一条边的指针
}EdgeNode;
typedef struct VertexNode//顶点信息
{
int data;
EdgeNode *firstedge;
}VertexNode,AdjList[MAXVEX];
typedef struct //邻接表
{
AdjList adjList;
int numVertexes,numEdges;//顶点数和边数
}GraphAdjList;
邻接表由两部分组成:
1)表头节点表AdjList[MAXVEX]:可以随机访问任一顶点的边链表,结点由数据域和指针域组成。

2)边表(边结点)EdgeNode:边链表中边结点包括邻接点域、数据域和链域三部分。
1.邻接点域指示与顶点邻接的点在图中的位置;
2.数据域存储权值等;
3.链域指示与顶点邻接的下一条边的结点(类似于单链表中的next指针)。

创建无向图的邻接表
void CreateALGraph(GraphAdjList *G)
{
EdgeNode *e;
int x,y,w;
cout<<"输入顶点数和边数:"<<endl;
cin>>G->numVertexes>>G->numEdges;
for (int i = 0; i < G->numVertexes; i++)
{
cin>>G->adjList[i].data;
G->adjList[i].firstedge=NULL;
}
for (int i = 0; i < G->numEdges; i++)
{
cout<<"输入边的下标以及权值:"<<endl;
cin>>x>>y;
e=(EdgeNode*)malloc(sizeof(EdgeNode));
e->adjvex=y;
e->next=G->adjList[x].firstedge;//头插法插入结点
G->adjList[x].firstedge=e;
e=(EdgeNode*)malloc(sizeof(EdgeNode));
e->adjvex=x;
e->next=G->adjList[y].firstedge;
G->adjList[y].firstedge=e;
}
}
遍历边集,边(x,y)分别将x和y添加到对方的邻接表中。
邻接表优点:
①便于增加和删除顶点。
②便于统计边的数目。
③空间效率高。
缺点:
①不便于计算各个顶点数入度出度。
②不便于判断顶点之间是否有边。
深度优先搜索DFS
深度优先搜索类似于树的前序遍历,是树的前序遍历推广到图。
它从图中某个顶点出发,访问此顶点并访问该顶点的第一个未被访问的邻接点,并以该顶点作为新顶点重复此过程。
从DFS的过程可以看出DFS是利用递归进行访问的。
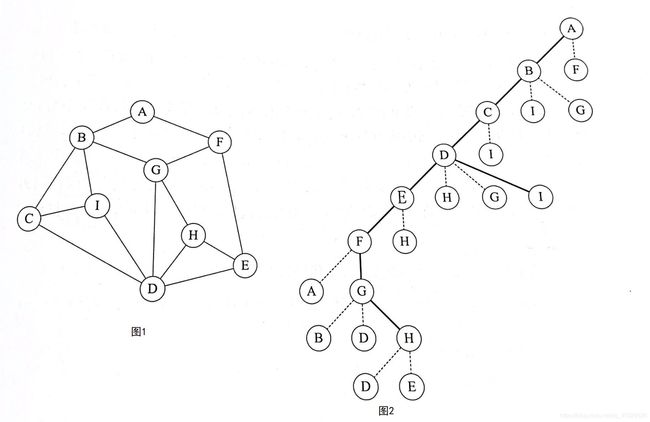
如图,图2为图1的DFS过程,实线走过的路径为图1的DFS生成树。
邻接矩阵的深度优先搜索
bool visited[MAXVEX];
void DFS(MGraph G,int i)
{
visited[i]=true;
printf("%c",G.vexs[i]);
for (int j = 0; j < G.numVerTexes; j++)
{
if(G.arc[i][j]!=0&&!visited[j])
DFS(G,j);
}
}
void DFSTraverse(MGraph G)
{
for (int i = 0; i < G.numVerTexes; i++)
{
visited[i]=false;
}
for (int i = 0; i < G.numVerTexes; i++)
{
if(!visited[i])
DFS(G,i);
}
}
我们需要设置访问标志数组visited[MAXVEX]来保存图中顶点的访问情况,初始化时所有顶点都没有被访问visited[i]=false
每次访问结点时,置该结点visited[i]=true,接着遍历如果两个顶点之间有边且该结点没有被访问过则DFS那个顶点。
与邻接矩阵相似,邻接表的DFS只是在访问时变成对链表进行访问:
邻接表的深度优先搜索
void DFS(GraphAdjList *GL,int i)
{
EdgeNode *p;
visited[i]=true;
printf("%c",GL->adjList[i].data);
p=GL->adjList[i].firstedge;//取出数据后访问边表
while (p)
{
if (!visited[p->adjvex])
{
DFS(GL,p->adjvex);
p=p->next;
}
}
}
void DFSTraverse(GraphAdjList *GL)
{
for (int i = 0; i < GL->numVertexes; i++)
{
visited[i]=false;
}
for (int i = 0; i < GL->numVertexes; i++)
{
if(!visited[i])
DFS(GL,i);
}
}
访问顶点后,对该顶点的边表进行访问,最终访问完第一个顶点边表中的所有节点即遍历了一个连通分支。
如果该图为连通图则只需要在DFSTraverse()中执行一次DFS就可以遍历整个图。
广度优先搜索BFS
广度优先搜索类似于树的层序遍历,是树的层序遍历推广到图。
它从图中某个顶点出发,访问这个顶点各个未曾访问过的邻接点,再从这些邻接点出发依次访问它们的邻接点,使先被访问的顶点的邻接点先于后被访问的顶点的邻接点被访问。
BFS算法的实现需引进队列保存已被访问过的顶点。

如图,图2实线走过的路径为图1的BFS生成树,下图顶点进入弹出队列先后顺序展示图1的BFS过程。
邻接矩阵的广度优先搜索
void BFSTraverse(MGraph G)
{
Queue Q;
for (int i = 0; i < G.numVerTexes; i++)
{
visited[i]=false;
}
InitQueue(&Q);
for (int i = 0; i < G.numVerTexes; i++)
{
if (!visited[i])
{
visited[i]=true;
cout<<G.vexs[i]<<endl;
EnQueue(&Q,i);
while (!QueueEmpty(Q))
{
DeQueue(&Q,&i);//取出队头元素并将其下标赋值给i
for (int j = 0; j < G.numVerTexes; j++)
{
if (G.arc[i][j]!=0&&!visited[j])
{
visited[j]=true;
cout<<G.vexs[j];
EnQueue(&Q,j);
}
}
}
}
}
}
和DFS类似,BFS也需要一个visited数组标记顶点的访问状态。
首先找到第一个没有被访问的顶点,置visited[i]=true标记这个顶点已经被访问过,输出顶点后将其加入队列;
接着循环只要队列不为空,则取出队头顶点;
循环遍历如果和队头顶点有边相连则标记该顶点已被访问过且将这个顶点加入队列;
直到队列为空则走完了一个连通分支。
与邻接矩阵相似,邻接表的BFS只是在访问时变成对链表进行访问:
邻接表的广度优先搜索
void BFSTraverse(GraphAdjList *GL)
{
EdgeNode *p;
Queue Q;
for (int i = 0; i < GL->numVertexes; i++)
{
visited[i]=false;
}
InitQueue(&Q);
for (int i = 0; i < GL->numVertexes; i++)
{
if (!visited[i])
{
visited[i]=true;
cout<<GL->adjList[i].data;
EnQueue(&Q,i);
while (!QueueEmpty(Q))
{
DeQueue(&Q,&i);
p=GL->adjList[i].firstedge;
while (p)
{
if (!visited[p->adjvex])
{
visited[p->adjvex]=true;
cout<<GL->adjList[p->adjvex].data;
EnQueue(&Q,p->adjvex);
}
p=p->next;
}
}
}
}
}
首先找到第一个没有被访问的顶点,置visited[i]=true标记这个顶点已经被访问过,输出顶点后将其加入队列;
接着循环只要队列不为空,则取出队头顶点;
指针p指向队头顶点的边表中的第一个结点,只要p不为空就执行循环;
只要队头顶点边表中的顶点没有被访问,就标记这个顶点已经被访问、取出数据、并将其加入队列;
直到p为空说明访问完队头顶点的整个边表,此时和队头顶点相邻的所有顶点已经被访问;
不断重复操作,当队列为空时则遍历完一个连通分支。
总结
DFS和BFS应用非常广泛,不仅仅限于在邻接矩阵和邻接表中搜索,在图论中求迷宫问题、连通分支个数、最短路径等问题都有体现。