动态规划（0-1背包问题）

1.问题给定的已知：

有编号分别为1,2,3,4,5的物件物品，他们的重量分别是2，2,6,5,4，他们的价值分别是6,3,5,4,6，先给一格承重为10的背包。

2.所求目标：

如何让背包里装入的物品具有最大的价值总和

3.数学模型：

①建立模型：即求max（v1x1 + v2x2 + … + vnxn）
②约束条件：W1X1 + W2X2 + … + WnXn < capacity

4.最优子结构分析：

假设是所给0-1背包问题的一个最优解，则是下面相应子问题的一个最优解：
约束条件：

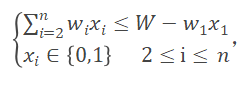
目标函数：

证明：利用反证法，设(X2,…Xn)不是上述子问题的一个最优解，而(y2,…yn)是，则后者目标函数值要大于前者。即
又因为前者满足上述约束条件，说明(x1,y2,…,yn)是原问题的一个解。
在不等式
两边同时加上v1x1则有
说明(x1,x2,…xn)非原问题最优解。这与(x1,x2,…,xn)是原问题最优解相悖。所以(x2,…,xn)是子问题最优解，最优子结构性质得证。

5.建立最优值的递归关系式：

由于0-1背包问题的解是用向量(x1,x2,…,xn)来描述的。因此，该问题可以被看作决策一个n元0-1向量(x1,x2,…,xn)。对于任意一个分量的决策是“决定xi=1或xi=0”，i=1,2,…,n。对决策后，序列(x1,x2,…,xi-1)已经被确定，在决策xi时，问题处于下列两种状态之一：

①背包容量不足以装入物品i，则xi=0，装入背包的价值不增加
②背包容量足以装入物品i，则xi=1，装入背包的价值增加vi

在这两种情况下，装入背包的价值最大者应该是对xi决策后的价值。
令C[i][j]表示子问题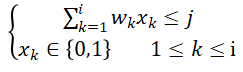
的最优值，即C[i][j]=max。那么，C[i+1][j-wixi]表示该问题的子问题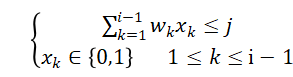
的最优值，如果j=0或i=0，令C[0][j]=C[i][0]=0，1≤i≤n，1≤j≤W；如果j＜，第i个物品肯定不能装入背包，xi=0，此时C[i][j]=C[i-1][j-wixi]=C[i-1][j]；如果j≥wi，第i个物品能够装入背包；如果第i个物品不装入背包，即=0，则C[i][j]=C[i-1][j-wixi]=C[i-1][j]；如果第i个物品装入背包，即=1，则C[i][j]=C[i-1][j-wixi]+vi=C[i-1][j-wi]+vi。可见当j≥wi时，C[i][j]应取二者的最大值，即max{C[i-1][j],C[i-1][j-wi]+vi}。
由此可得，最优值的递归关系式为

6.自底向上求解：

1）数据结构：

存储物品的重量w[]及价值v[]为线性表，最大价值表V[][]为二维数组。

2）程序代码：

#include
using namespace std;

#define C 10
int V[6][11];
int x[5];
int KnapSack(int n, int w[], int v[]);
int max(int x, int y);
int main()
{
	int w[] = { 2, 3, 4, 5, 6 };
	int v[] = { 3, 4, 5, 6, 7 };
	
	cout << "背包的最大价值为:" << KnapSack(5, w, v) << endl;
	return 0;
}

int max(int x, int y){
	if (x>y)
	{
		return x;
	}
	else
	{
		return y;
	}
}

int KnapSack(int n, int w[], int v[]){
	int i, j;

	//1.初始化第0列
	for ( i = 0; i <=n; i++)
	{
		V[i][0] = 0;
	}

	//2.初始化第0行
	for ( j = 0; j <=C; j++)
	{
		V[0][j] = 0;
	}

	//3.初始化第i行，进行i次迭代
	for (i = 1; i <=n; i++)
	{
		for ( j = 1; j <= C; j++)
		{
			if (j<w[i-1])
			{
				//第j个物品重量大加不进去
				V[i][j] = V[i - 1][j];
			}
			else
			{
				V[i][j] = max(V[i - 1][j], V[i-1][j-w[i-1]]+v[i-1]);
			}
		}
	}
	//4.返回背包的最大价值
	return V[n][C];
} 

3）测试数据：

w[] = { 2, 2, 6, 5, 4 } v[] = { 6, 3, 5, 4, 6 } C = 10

w[] = { 2, 3, 4, 5, 6 } v[] = { 3, 4, 5, 6, 7 } C = 10

4）结果分析：

结果正确性
由上图结果可得，结果正确。
时间复杂度
在构建最大价值表V[n][C]时，初始化列时间复杂度为O(n)、初始化行时间复杂度为O©、迭代剩余空行时，时间复杂度为O(nC)。
综上所述，程序时间复杂度为O(n)+ O©+O(nC) =O(nC)。

7.根据相关信息构造最优解：

1）程序代码：

#include
using namespace std;

#define C 10
int V[6][11];
int x[5];
int KnapSack(int n, int w[], int v[]);
int max(int x, int y);
void printV();
int main()
{
	int w[] = { 2, 2, 6, 5, 4 };
	int v[] = { 6, 3, 5, 4, 6 };
	
	cout << "背包的最大价值为:" << KnapSack(5, w, v) << endl;
	cout << "装入背包的物品是:";
	for (int i = 0; i < 5; i++)
	{
		if (x[i]==1)
		{
			cout << "物品" << i + 1;
		}
		
	}
	printf("\n");
	printV();
	cout << endl;
	return 0;
}

int max(int x, int y){
	if (x>y)
	{
		return x;
	}
	else
	{
		return y;
	}
}

int KnapSack(int n, int w[], int v[]){
	int i, j;

	//1.初始化第0列
	for ( i = 0; i <=n; i++)
	{
		V[i][0] = 0;
	}

	//2.初始化第0行
	for ( j = 0; j <=C; j++)
	{
		V[0][j] = 0;
	}

	//3.初始化第i行，进行i次迭代
	for (i = 1; i <=n; i++)
	{
		for ( j = 1; j <= C; j++)
		{
			if (j<w[i-1])
			{
				//第j个物品重量大加不进去
				V[i][j] = V[i - 1][j];
			}
			else
			{
				V[i][j] = max(V[i - 1][j], V[i-1][j-w[i-1]]+v[i-1]);
			}
		}
	}

	//4.求装入的物品
	for ( j = C,i=n; i>0; i--)
	{
		if (V[i][j]>V[i-1][j])
		{
			x[i-1] = 1;
			j = j - w[i-1];
		}
		else
		{
			x[i-1] = 0;
		}
	}

	//5.返回背包的最大价值
	return V[n][C];
}

void printV(){
	for (int i = 0; i < 6; i++)
	{
		for (int j = 0; j < C+1; j++)
		{
			if (j==0)
			{
				printf("%d\t", i);
			}
			else
			{
				printf("%d\t", V[i][j]);
			}
		}
		printf("\n");
	}
} 

2）测试数据及结果：

w[] = { 2, 2, 6, 5, 4 }
v[] = { 6, 3, 5, 4, 6 }
C = 10

w[] = { 2, 3, 4, 5, 6 }
v[] = { 3, 4, 5, 6, 7 }
C = 10

3）结果分析：

结果正确性
由上图结果及最大价值表可得，结果正确。
时间复杂度
在构建最大价值表V[n][C]时，初始化列时间复杂度为O(n)、初始化行时间复杂度为O©、迭代剩余空行时，时间复杂度为O(nC)。
求装入物品x[]时，时间复杂度为O(n)。
打印最大价值表V[][]时，时间复杂度为O(nC)。
综上所述，程序时间复杂度为O(n)+ O©+O(nC)+O(n)+O(nC)=O(nC)。

8.总结：

一个问题可以用动态规划法求解的先决条件：
1、最优子结构性质：当问题的最优解包含了其子问题的最优解时，成该问题具有最优子结构性质。
2、重叠子问题：每次产生的子问题并不总是新问题，有些子问题被反复计算多次。
满足了以上两个条件的问题可以考虑用动态规划法求解，他是一种自底向上的递归算法。