初识二叉树
目录
树是什么
二叉树
两种特殊的二叉树
二叉树的性质
二叉树的存储
二叉树的遍历
小结
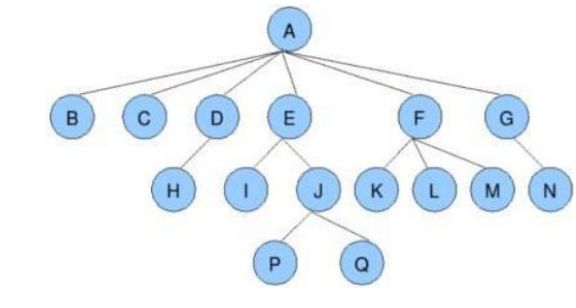
树是什么
主要概念:
双亲结点或者父节点:若一个节点含有子节点,则称该节点为子节点的父节点。(如上图A为B的父节点)
孩子节点或者子节点:一个节点含有的子树的根节点称为该节点的子节点。(如B节点为A节点的子节点)
根节点:没有父节点的节点(A)。
叶节点:没有子节点也就是度为0的节点(上图的B、C等)
节点的度:一个节点含有子节点的个数称为该节点的度。(例如A的度为6,D的度为1)
树的度:一棵树中最大节点的度称为树的度。(上图树的度为6)
根结点 :一棵树中,没有双亲结点的结点。(如上图: A)节点的层次 :从根开始定义起,根为第 1 层,根的子节点为第 2 层,以此类推。树的深度和高度:高度为最大深度。
二叉树
概念
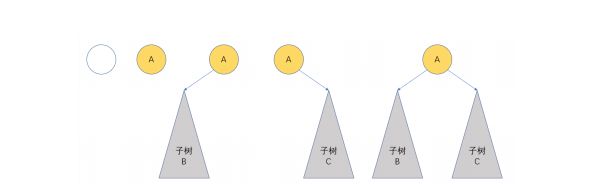
基本形态:
两种特殊的二叉树
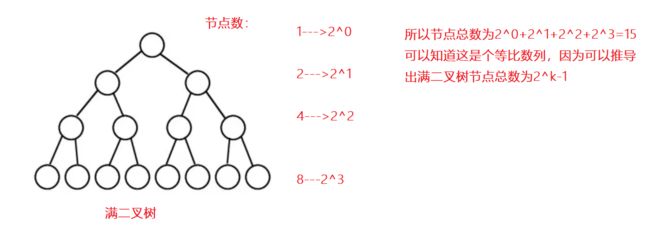
1、满二叉树:一个二叉树,如果每一个层的结点数都达到最大值,则这个二叉树就是满二叉树。
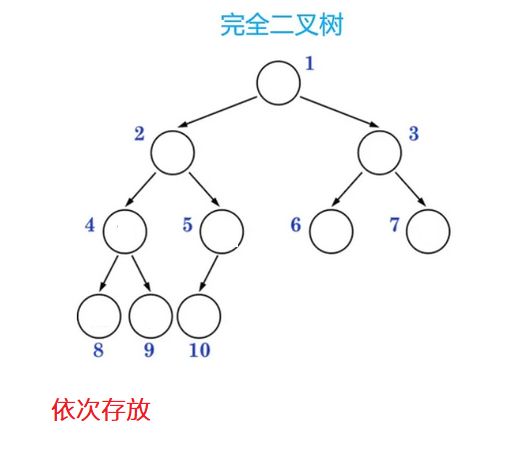
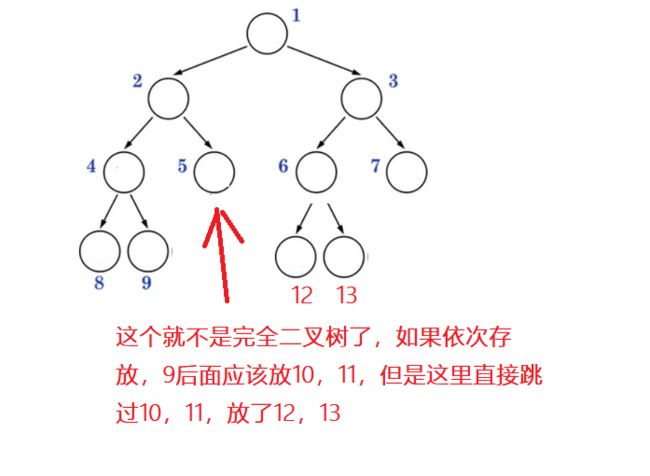
2、完全二叉树
举个反例:
二叉树的性质
若规定根节点的层数为1,则一棵非空二叉树的第i层上最多有 2^(i-1)(i>0)个结点。
例题1:
1、某二叉树共有399个结点,其中有199个度为2的结点,则该二叉树中的叶子结点数为( B)
A、不存在这样的二=叉树
B、200
C 、198
D、 199
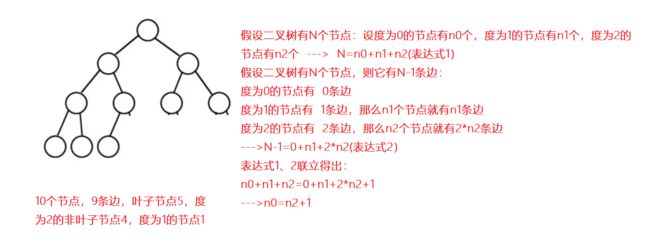
由2可知度为2(n2)的结点个数为199,则根据公式n0=n2+1;所以该二叉树中叶子结点数为200。
例题2:
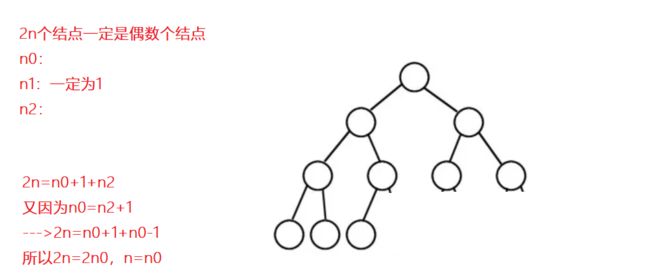
2、在具有2n个结点的完全二叉树中,叶子结点个数为(A )
A、n
B、 n+1
C 、n-1
D 、n/2
解题思路:
例题3:
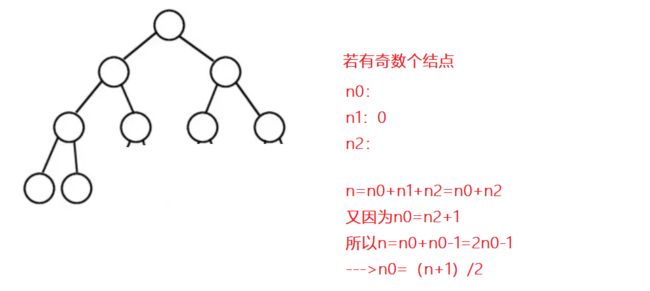
3、一个具有767个节点的完全二叉树,其叶子节点个数为(B)
A、383
B、384
C、385
D、386
解题思路:
具有n个结点的完全二叉树的深度k为 log2(n+1)向上取整 。
对于具有n个结点的完全二叉树,如果按照从上至下从左至右的顺序对所有节点从0开始编号,则对于序号为i的结点有:
若子节点的编号为i,则父节点编号为(i-1)/2;
若父节点的编号为i,则左孩子节点编号为2i+1,右节点编号为2i+2;
二叉树的存储
二叉树的链式存储是通过一个一个的节点引用起来的,常见的表示方式有二叉和三叉表示方式,具体如下:
// 孩子表示法
class TreeNode {
int val; // 数据域
TreeNode left; // 左孩子的引用,常常代表左孩子为根的整棵左子树
TreeNode right; // 右孩子的引用,常常代表右孩子为根的整棵右子树
}
// 孩子双亲表示法
class TreeNode {
int val; // 数据域
TreeNode left; // 左孩子的引用,常常代表左孩子为根的整棵左子树
TreeNode right; // 右孩子的引用,常常代表右孩子为根的整棵右子树
TreeNode parent; // 当前节点的根节点
}接下来的操作一般都是用孩子表示法。
二叉树的遍历
1、前序遍历(根节点-->左节点-->右节点)
递归实现(遍历结果放list里面)
public List preorderTraversal(TreeNode root) {//给根节点来遍历数组
List list=new ArrayList<>();
if(root==null){
return list;
}
list.add(root.val);
List left=new ArrayList<>();
left=preorderTraversal(root.left);
list.addAll(left);
List right=new ArrayList<>();
right=preorderTraversal(root.right);
list.addAll(right);
return list;
} 2、中序遍历(左节点-->根节点-->右节点)
递归实现(遍历结果放list里面)
public List inorderTraversal(TreeNode root) {
List list=new ArrayList<>();
if(root==null){
return list;
}
List left=inorderTraversal(root.left);
list.addAll(left);
list.add(root.val);
List right=inorderTraversal(root.right);
list.addAll(right);
return list;
} 3、后序遍历(左节点-->右节点-->根节点)
递归实现(遍历结果放list里面)
public List postorderTraversal(TreeNode root) {
List list=new ArrayList<>();
if(root==null){
return list;
}
List left=postorderTraversal(root.left);
list.addAll(left);
List right=postorderTraversal(root.right);
list.addAll(right);
list.add(root.val);
return list;
} 4、层序遍历
public List> levelOrder(TreeNode root) {
List> ret= new ArrayList>();
if(root==null){
return ret;
}
Queue queue=new LinkedList();
queue.offer(root);
while(!queue.isEmpty()){
List list=new ArrayList<>();
int size=queue.size();
for(int i=0;i 小结
以上就是今天的内容了,有什么问题大家都可以在评论区留言哦✌✌✌