独孤九剑第七式-物以类聚 人以群分（K-means模型）

文章适合于所有的相关人士进行学习
各位看官看完了之后不要立刻转身呀
期待三连关注小小博主加收藏
小小博主回关快 会给你意想不到的惊喜呀
各位老板动动小手给小弟点赞收藏一下，多多支持是我更新得动力！！！

---

前言

今天我们来说一个比较简单的模型，一个好汉三个帮的模型，也就是K-means算法模型，他是属于无监督的机器学习模型，那么什么是有监督，什么是无监督呢？我对于这种官方词汇一直是比较反感的，无监督就是所求的问题没有因变量y就是无监督。对于无监督的数据挖掘算法，最为典型的就是聚类算法了。

K-means模型讲解

⚡️K-means模型思想

K-means聚类算法利用距离的远近的思想作为数据聚为指定的k个簇，进而使样本呈现簇内之间差异较小，簇间差异较大的特征。

⚡️K-means聚类算法步骤

1.从数据中随机挑选k个样本点作为原始的簇中心。
2.计算剩余样本与簇中心的距离，并把各样本标记为离k个簇中心最近的类别。
3.重新计算各簇中样本点的均值，并以均值作为新的k个簇中心。
4.不断重复第二步和第三步，直到簇中心的变化趋于稳定，形成最终的k个簇。
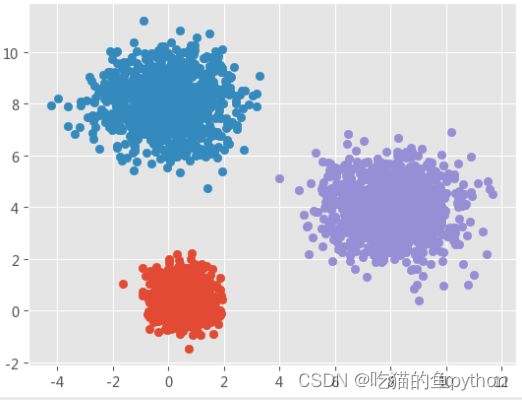
我知道各位一定不喜欢看文字的内容，那么我们上图：

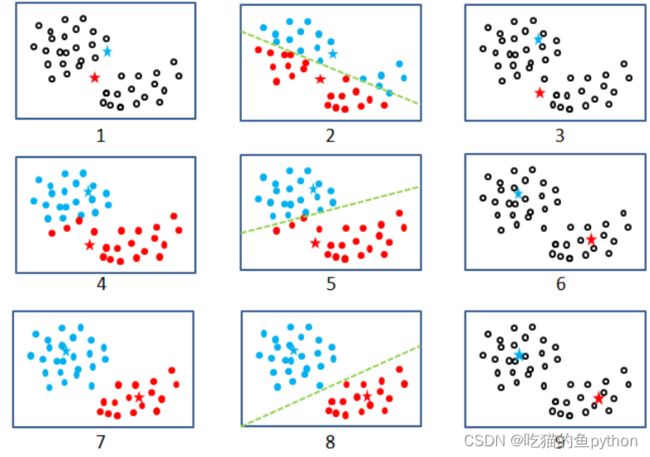
简单一点来说就是我们最开始随机找到两个点，然后分别计算其他的点和这两个点的距离，然后离得近就分为一类。然后我们分完类之后，把聚的两类找一个均值点，然后继续找所有的点和这两点距离最近，然后又分为一类，直到最后趋于稳定了。换点的这个思想就跟工作单位换领导一样！！！

⚡️K-means聚类算法数学推导

我们直到只有簇内样本越相似，说明了聚类效果越好，可以理解为簇内的样本点的距离簇内中心点的离差平方和越小就说明聚类效果越好！由此我们可以得到K-means的目标函数：

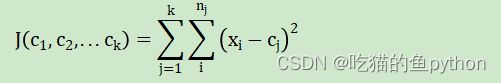
由于最近写论文用到了这个公式所以直接套用！
Cj表示簇中心，Xi表示j个簇中的样本，Nj表示j个簇内的样本总量。
我们既然想要求目标函数的最小值，那就属于老生常谈了，直接偏导：

令偏导数等于0：

我们最后得出的这个点恰恰就是样本的平均值，所以我们说的K-means不是瞎说的，为什么取均值，不去取别的数值呢，是由数学依据的！

K-means模型中K值得选取

⚡️拐点法

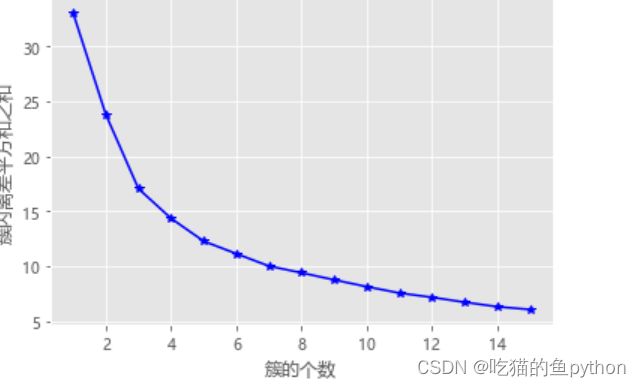
簇内离差平方和和拐点法得思想很简单，就是在不同得k值下我们计算簇内离差平方和，然后通过可视化得方法找到拐点，确定k值，当折线图得斜率突然有大变小，并且斜率在这之后就变缓了，就说明，这个点就是我们所要找的K点。

def k_SSE(X, clusters):
	 K = range(1,clusters+1)
	 TSSE = []
	 for k in K:
		 SSE = []
		 kmeans = KMeans(n_clusters=k)
		 kmeans.fit(X)
		 labels = kmeans.labels_
		 centers = kmeans.cluster_centers_
		 for label in set(labels):
		 SSE.append(np.sum((X.loc[labels == label,]-centers[label,:])**2))
		 # 计算总的簇内离差平方和
		 TSSE.append(np.sum(SSE))

比如这个案例我们得到的效果就是：

很明显就是K=3.

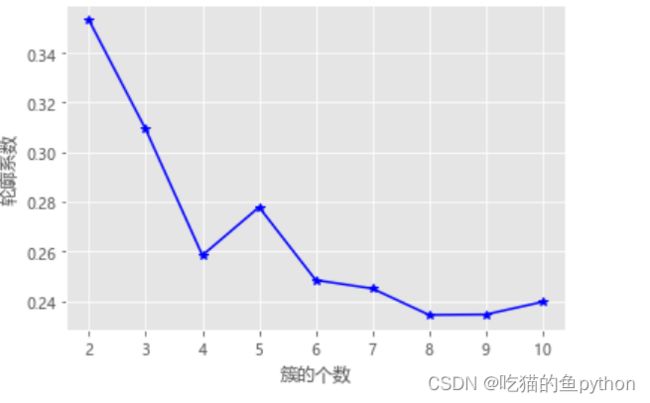
⚡️轮廓系数法

该方法综合考虑了簇得密集性和离散型两个信息，如果数据集被分割得非常理想，那么对应得簇内样本会很密集，簇间会很分散，计算公式可以表示为：

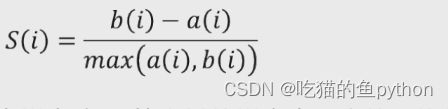
其中a(i)表示了密集型，b（i）表示了分散性。如果簇内样本越密集说明了a(i)应该趋近于0.如果簇间越分散，说明b(i）应该越趋近于1.根据这个思想我们可以得到，S（i）越趋近于1，说明效果越好，越趋近于0，说明进入了模糊地带，越不好。

def k_silhouette(X, clusters):
	 K = range(2,clusters+1)
	 # 构建空列表，用于存储不同簇数下的轮廓系数
	 S = []
	 for k in K:
		 kmeans = KMeans(n_clusters=k)
		 kmeans.fit(X)
		 labels = kmeans.labels_
		 # 调用子模块metrics中的silhouette_score函数，计算轮廓系数
		 S.append(metrics.silhouette_score(X, labels, metric='euclidean'))

python自带计算轮廓系数得函数。
结果如下：

K-means模型实战

⚡️数据

这是NBA球员得相关数据，我们对此进行聚类。

players = pd.read_csv(r'players.csv')
players.head()
#绘制散点图
sns.lmplot(x = '得分', y = '命中率', data = players, 
           fit_reg = False, scatter_kws = {'alpha':0.8, 'color': 'steelblue'})
plt.show()
#标准化处理数据及拐点法
from sklearn import preprocessing
# 数据标准化处理
X = preprocessing.minmax_scale(players[['得分','罚球命中率','命中率','三分命中率']])
# 将数组转换为数据框
X = pd.DataFrame(X, columns=['得分','罚球命中率','命中率','三分命中率'])
# 使用拐点法选择最佳的K值
k_SSE(X, 15)
#轮廓系数法
k_silhouette(X, 10)
#进行聚类
kmeans = KMeans(n_clusters = 3)
kmeans.fit(X)
# 将聚类结果标签插入到数据集players中
players['cluster'] = kmeans.labels_
# 构建空列表，用于存储三个簇的簇中心
centers = []
for i in players.cluster.unique():
    centers.append(players.loc[players.cluster == i,['得分','罚球命中率','命中率','三分命中率']].mean())
# 将列表转换为数组，便于后面的索引取数
centers = np.array(centers)

# 绘制散点图
sns.lmplot(x = '得分', y = '命中率', hue = 'cluster', data = players, markers = ['^','s','o'],
           fit_reg = False, scatter_kws = {'alpha':0.8}, legend = False)
# 添加簇中心
plt.scatter(centers[:,0], centers[:,2], c='k', marker = '*', s = 180)
plt.xlabel('得分')
plt.ylabel('命中率')
# 图形显示
plt.show()

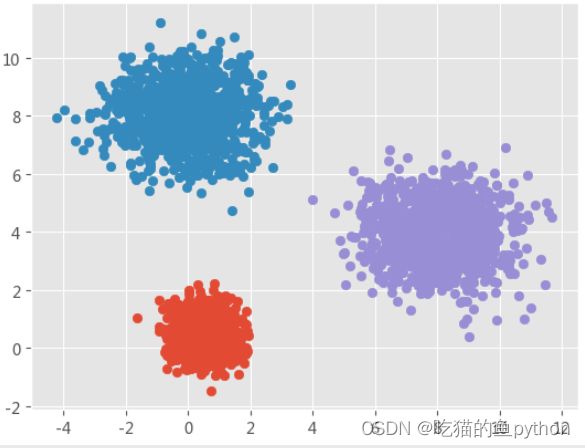
⚡️结果展示

拐点法结果

轮廓系数法结果

K-means聚类结果

文章适合于所有的相关人士进行学习
各位看官看完了之后不要立刻转身呀
期待三连关注小小博主加收藏
小小博主回关快 会给你意想不到的惊喜呀
各位老板动动小手给小弟点赞收藏一下，多多支持是我更新得动力！！！