【自动驾驶】全局路径规划算法——Dijkstra算法

参考资料

• 路径规划与轨迹跟踪系列算法学习
• 最短路径算法-迪杰斯特拉(Dijkstra)算法
• 迪杰斯特拉dijkstra算法的python实现
• Python实现迪杰斯特拉算法

1. 基本概念

1.1 算法简介

迪杰斯特拉算法(Dijkstra)是由荷兰计算机科学家狄克斯特拉于1959 年提出的，因此又叫狄克斯特拉算法。是从一个节点遍历其余各节点的最短路径算法，解决的是有权图中最短路径问题。

它的主要特点是以起始点为中心向外层层扩展(广度优先遍历思想)，直到扩展到终点为止。

1.2 算法思想

1. 设G=(V,E)是一个带权图，V为节点集合。通过Dijkstra计算图G中的最短路径时，需要指定一个起点(假设为D，即从顶点D开始计算)。
2. 此外，引进两个数组S和U。初始时S中只有一个起点，S的作用是记录已求出最短路径的节点(以及相应的最短路径长度)；而U则是记录还未确定最短路径的节点(以及该节点到起点D的距离)。
3. 初始时，数组S中只有起点D，而数组U中是除起点D之外的节点集合，并且数组U中记录各节点到起点D的距离。如果节点与起点D不相邻，距离设为无穷大。
4. 然后，从数组U中找出路径最短的节点K，并将其加入到数组S中；同时，从数组U中移除节点K。接着，更新数组U中的各节点到起点D的距离。
5. 重复第4步操作，直到遍历完所有节点。

1.3 算法图解

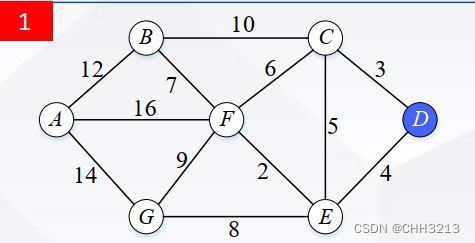
以上图为例，设节点D为起点。

1. 初始时，S只包含起点D；U包含除 D外的其他节点，且U中节点的距离为起点D到该节点的距离，如果该节点与起点D不相邻，距离为无穷大。

   

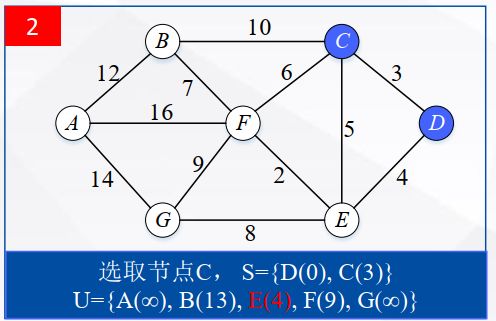
2. 从U中选出距离最短的节点C，并将节点C加入到S中；同时，从U中移除节点C。然后，更新U中各个节点到起点D的距离。

   之所以更新U中节点的距离，是由于确定了C是求出最短路径过程中的节点，从而可以利用C来更新其它节点的距离；因为因为起点D到节点v的距离(D,v)可能大于(D,C)+(C,v)的距离。

   

接下来重复步骤1，2即可。

3. 选取节点E，将E加入到S中，同时更新U中节点的距离。以节点F为例，之前F到D的距离为9；但是将E加入到S之后，F到D的距离为6=(F,E)+(E,D)。
   

4. 将节点F加入到S中，同时更新U。
   

5. 将节点G加入到S中，同时更新U。
   

6. 将节点B加入到S中，同时更新U。
   

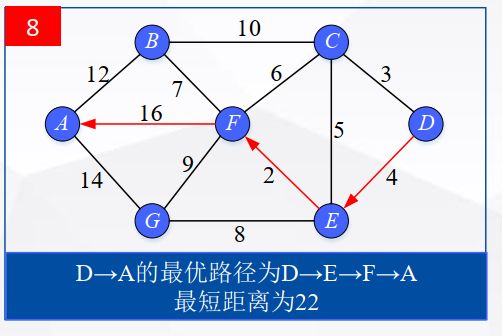
7. 将节点A加入到S中，同时更新U。
   
   此时，起点D到各个节点的最短距离就计算出来了：A(22) B(13) C(3) D(0) E(4) F(6) G(12)。

8. 最后D->A的最优路径为D->E->F->A
   

1.4 最短路径的最优子结构性质

如果$P(i,j)=\{V_i\dots V_k\dots V_m\dots V_j\}$是从顶点$i$到$j$的最短路径，$k$和$m$是这条路径上的一个中间顶点，那么$P(k,m)$必定是从$k$到$m$的最短径。

证明：

假设$P(i,j)=\{V_i\dots V_k\dots V_m\dots V_j\}$是从顶点$i$到$j$的最短路径，则有$P(i,j)=P(i,k)+P(k,m)+P(m,j)$。而$P(k,m)$不是从$k$到$m$的最短距离，那么必定存在另一条从$k$到$m$的最短路径$P^{\prime }(k,m)$，那么$P(i,j)=P(i,k)+P^{\prime }(k,m)+P(m,j)<P(i,j)$。则与$P(i,j)$是从$i$到$j$的最短路径相矛盾。因此该性质得证。

2. python代码实现

参考自资料。

def dijkstra(matrix, source):
    """迪杰斯特拉算法实现
    Args:
        matrix (_type_): 用邻接矩阵表示带权图
        source (_type_): 起点

    Returns:
        _type_: 最短路径的节点集合，最短路径的节点的最短距离，每个节点到起点的最短路径
    """
    INF = float('inf')
    n = len(matrix)
    m = len(matrix[0])
    assert n == m, "Error, please examine matrix dim"
    assert source < n, "Error, start point should be in the range!"
    S = [source]        # 已找到最短路径的节点集合
    U = [v for v in range(n) if v not in S]  # 记录还未确定最短路径的节点集合
    distance = [INF] * n          # source到已找到最短路径的节点的最短距离
    distance[source] = 0  # 起点到自己的距离
    path_optimal = [[]]*n           # source到其他节点的最短路径
    path_optimal[source] = [source]
    while len(S) < n:   # 当已找到最短路径的节点小于n时
        min_value = INF
        col = -1
        row = -1
        for s in S:     # 以已找到最短路径的节点所在行为搜索对象
            for u in U:   # 从U中搜索尚未记录的节点
                if matrix[s][u] + distance[s] < min_value:  # 找出最小值
                    # 在某行找到最小值要加上source到该行的最短路径
                    min_value = matrix[s][u] + distance[s]
                    row = s         # 记录所在行列
                    col = u
        if col == -1 or row == -1:  # 若没找出最小值且节点还未找完，说明图中存在不连通的节点
            break
        S.append(col)  # 在S中添加已找到的节点
        U.remove(col)  # 从U中移除已找到的节点
        distance[col] = min_value # source到该节点的最短距离即为min_value
        path_optimal[col] = path_optimal[row][:]    # 复制source到已找到节点的上一节点的路径
        path_optimal[col].append(col)       # 再其后添加已找到节点即为source到该节点的最短路径
    return S, distance, path_optimal


def main():
    INF = float('inf')
    # 使用邻接矩阵存储图
    # A B C D E F G
    matrix = [[0, 12, INF, INF, INF, 16, 14],
            [12, 0, 10, INF, INF, 7, INF],
            [INF, 10, 0, 3, 5, 6, INF],
            [INF, INF, 3, 0, 4, INF, INF],
            [INF, INF, 5, 4, 0, 2, 8],
            [16, 7, 6, INF, 2, 0, 9],
            [14, INF, INF, INF, 8, 9, 0]]
    S, distance, path_optimal = dijkstra(matrix, 3)
    print('S:')
    print(S)
    print('distance:')
    print(distance)
    print('path_optimal:')
    for p in path_optimal:
        print(p)

if __name__ == '__main__':
    main()

详细请见github仓库