ResNet论文翻译及解读

摘要

​ 更深层次的神经网络更难训练。 我们提出了一个残差学习框架，以简化更深网络的训练。 我们明确地重构了每层相对于本层输入的学习残差函数，而不是学习无参照的函数。 我们提供了全面的实验证据，表明这些残差网络更容易优化，并且可以从显着增加的深度中获得更高准确率。 在 ImageNet 数据集上，我们评估深度了高达 152 层的残差网络(ResNet-152)——比 VGG 网络深 8 层，但仍然具有较低的复杂度。这些残差网络的集成在 ImageNet 测试集上得到了 3.57% 的误差，该结果在 ILSVRC 2015 分类任务中获得第一名。 我们还对具有 100 层和 1000 层的 CIFAR-10 进行了分析。

​ 网络深度对于许多视觉识别任务至关重要。仅仅因为网络极深的构造，我们在 COCO 物体检测数据集上获得了 28% 的相对提高。 深度残差网络是我们提交结果给 ILSVRC 和 COCO 2015 比赛的基础，我们还在 ImageNet 检测、ImageNet 定位、COCO 检测和 COCO 分割任务中获得了第一名。

一、介绍

​ 网络深度对于准确率的提升非常必要，领先的网络模型都在用深层网络（16~30层不等）。在此基础上出现了问题1：直接简单粗暴的堆积网络就能够使得网络模型效果变好吗？是梯度消失、爆炸这个困难一直困扰着这个问题的解决，因为梯度消失、爆炸从一开始就阻碍了收敛，然后这个问题已经在很大程度上通过归一初始化（权重初始化：Xavier初始化、MSRA初始化）和中间的归一化层得到解决，这使得具有数十层的网络能够以具有反向传播的SGD方法收敛。

如何解决梯度消失问题？

答：用到权重初始化+批归一化，既可以防止梯度消失，又可以加快网络收敛速度。

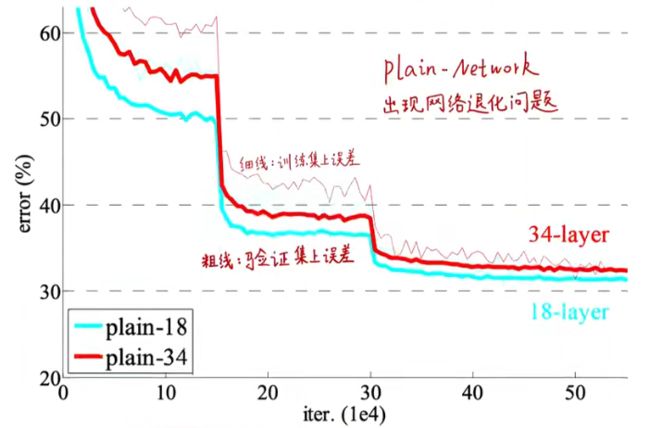
​ 问题2：随着网络收敛，会出现退化问题（退化不是由梯度消失、过拟合引起的），增加更多的层到适当深度的网络只会导致更高的错误率，这表明了不是所有的系统都能被相似的优化。实验很好地证明了这一点，如下图所示。这篇文章对于退化问题的解决方案是提出了一个深度残差学习架构。模型不需要直接拟合底层的映射，而是去拟合相对于输入的残差。

网络退化现象解释：随着网络深度的增加，准确率开始达到饱和并且在之后会迅速下降。

残差块

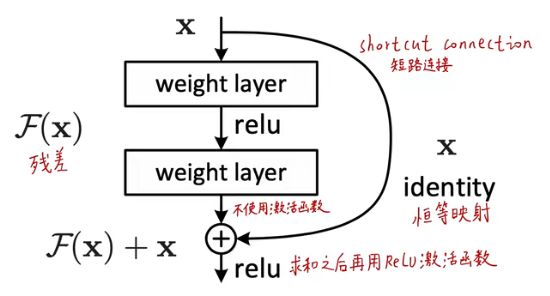
KaTeX parse error: Undefined control sequence: \mbox at position 2: \̲m̲b̲o̲x̲{原来的神经网络需要拟合一个底…

​ 假设优化残差映射要比优化底层映射容易，极端情况是如果恒等映射是最优的话，将残差模块的权重都调成0比直接拟合一个恒等映射（由非线性层堆叠而成）要容易（因为神经网络映射恒等映射的能力是非常差的，即让输出保持和输入一致是很难的），此时底层映射就是恒等映射。

​ 在论文中，shortcut连接简单表现为恒等映射，将恒等映射和残差相加得到最终的输出。恒等映射不会引入额外的参数量和计算量，整个网络可以用反向传播的随机梯度下降方法端到端地训练，可以用常见的深度学习框架(Caffe)进行处理而不需要再用其他求解器。

​ 在残差网络中得出的结论为：①极深残差网络易于优化收敛；②解决了退化问题；③可以在很深的同时提升准确率。

三、深度残差网络

1、残差网络

​ 用到万能近似定理（只要有一个隐含层的神经网络，理论上就可以拟合任何函数），即多个非线性层可以逐渐拟合复杂的函数，这就等价于要逐渐逼近一个残差函数F(x):=H(x)-x（假设输入和输出维度相同），不需要去直接学习底层函数H(x)，因此底层函数也就因此变成了F(x)+x。

​ 在介绍中提到了**传统网络中的多个非线性层难以拟合恒等映射，如果增加的层可以拟合恒等映射的话，那么它的训练错误率至少不会比浅层网络更差。通过残差学习的重构，如果恒等映射已经最优，那么残差模块只需要拟合零映射，求解器只需要使得多个和非线性层的权重为0以此去接近恒等映射，最终效果就是残差模块可以拟合恒等映射。**但实际情况下恒等映射都不会是最优的，本文设计的残差模块会对输入进行预处理，后面的网络只需要拟合前面网络的输出与期望函数的残差（H(x)-x）即可。下图表示残差模块输出的响应较小（因为扰动较小，所以响应也小）。

2、通过shortcut连接传递自身映射

​ 在每一个堆叠层都采用了残差学习，残差块用数学公式表示为：
$$y=F(x，[W_i])+x(1)$$
​ 在这里x是当前层的输入相量，y是当前层的输出向量，式子F(x, {Wi})代表要学习的残差映射，比如在这篇博客的第二张图中有两层。

​ 第二张图用残差函数公式表示为：
$$F=W_2\sigma (W_{1}x)(2)$$
​ sigma代表ReLU激活函数，这个式子的意思从图中可以看出是：输入x→权重层1→ReLU→权重层2。为了简化记号，我们忽略偏置项，操作F+x是通过shortcut连接的方式逐元素相加，然后对求和结果再用一次ReLU非线性激活。在这里需要注意的是式(1)中x和F的维度要相同，如果不是这种情况（当改变输入、输出通道数时），我们通过shortcut连接实施线性投影（Ws）以匹配维度，这里Ws为方阵，即式子变换为下式：
$$F(x，[W_i])+W_{s}x(3)$$
​ 只有要用到维度匹配的时候再用式(3),不到万不得已不要用。

​ 残差F的构造形式是灵活的，下图中有两层和三层的构造方式（更多层也是可以的），但是如果残差F只有一层，那么式(1)就相当于一个线性层，但是这样的构造不会有太大的收益。表示式为：
$$y=W_{1}x+x(4)$$

​ 上面的式子不仅针对全连接层，还可以应用到卷积层中，函数F(x,{Wi})可以表示多个卷积层，因此逐元素加法的实施是在两个特征图上逐元素、逐通道相加。

3、网络架构

3.1、无残差网络

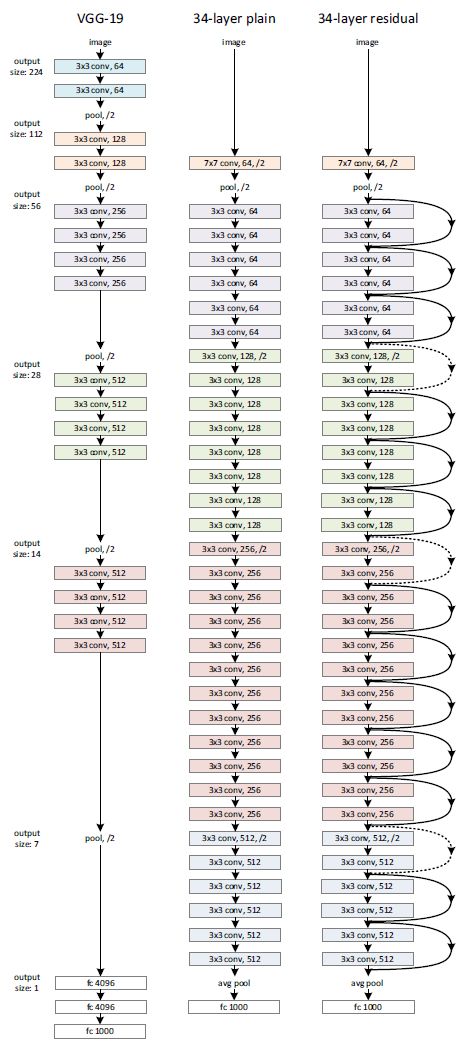
此网络设计灵感来源于VGGnet，卷积层大部分是3×3卷积核且设计规则为：

1）对于相同大小的输出特征图，该层应具有相同数量的卷积核（即每一个block内卷积核数量不变）；

2）如果特征图大小减半，卷积核的数量会增加一倍，以保持每层的时间复杂度。以上两个设计规则同VGG（VGG里就是每个block卷积核个数一样，且进入到下一个block时特征图大小减半且卷积核个数翻倍）。

​ 我们通过步长为2的卷积核直接进行了下采样，网络最后是一个GAP层和一个1000类别的带有softmax的FC层，总的带权重层数为34。

​ 值得注意的是这个模型较VGG-19卷积核数量更少、复杂度更低、FLOPs也更小。

3.2、残差网络

基于上述无残差网络，加入了short connection使得网络变为了对应的残差网络。

当输入和输出维度相同时可以直接使用恒等shortcut连接（式(1)）,如下最右图的实线shortcut连接所示。

当维度增加时即下采样时（用下图虚线的shortcut连接方式），有两个选择：

A：shortcut路仍执行恒等映射，此时要用padding补零使得维度增加，此方案没有引入额外的参数；

B：用式(3)投影shortcut来匹配维度（通过1×1卷积来完成）

对于这两个选项，当shortcut通过两个不同大小的特征图时，shortcut分支第一个卷积层步幅均设为2，即下采样卷积核步幅为2。

4、实施方案

4.1、训练阶段：与AlexNet和VGGnet类似。

数据集处理：图像的短边被随机采样到[256,480]以做尺度增强，在此基础上做224×224裁剪对上述图像做随机采样或做的水平翻转，在每个像素上做去均值操作和标准化的颜色增强（同AlexNet）。

加速网络收敛：在每个卷积层后和激活函数前都加入BN层。

权重初始化：遵循PReLU方法从头训练无残差和残差网络。

优化器：大小为256的mini-batch的随机梯度下降（SGD）。

学习率：初始为0.1，当错误率达瓶颈就乘0.1。

迭代次数：60万迭代轮次。

其他参数设置：权重衰减为0.0001，动量为0.9。

解决过拟合：不适用Dropout，因为BN和Dropout单独使用作用更佳，不能同时存在。

4.2、测试阶段：与AlexNet类似

​ 采用多尺度裁剪(10-crop)与结果融合的方法测试，即一张图片裁剪10个小图出来，并分别放到网络中得到10个结果，再将这10个结果汇总起来。在多个尺度图像上的结果取平均值（图像调整大小使得较短的边在{224，256，384，480，640}里面取值）

1、为什么要引入BN层？

我们在图像预处理过程中通常会对图像进行标准化处理，也就是image normalization，使得每张输入图片的数据分布能够统均值为u，方差为h的分布。这样能够加速网络的收敛。但是当一张图片输入到神经网络经过卷积计算之后，这个分布就不会满足刚才经过image normalization操作之后的分布了，可能适应了新的数据分布规律，这个时候将数据接入激活函数中，很可能一些新的数据会落入激活函数的饱和区，导致神经网络训练的梯度消失，如下图所示当feature map的数据为10的时候，就会落入饱和区，影响网络的训练效果。这个时候我们引入Batch Normalization的目的就是使我们卷积以后的feature map满足均值为0，方差为1的分布规律。在接入激活函数就不会发生这样的情况。

BN的作用有：①加速网络收敛速度 ②可以改善梯度消失问题

2、BN是怎样实施的？

首先会统计每个通道数目所有点的像素值，求得均值和方差，然后在每个通道上分别用该点的像素值减均值除方差得到该点的像素值，此过程就是BN。最后将其接入到激活函数中。

3、使用BN时需注意的问题？

（1）训练时要将traning参数设置为True，在验证时将trainning参数设置为False。在pytorch中可通过创建模型的model.train()和model.eval()方法控制。
（2）batch size尽可能设置大点，设置小后表现可能很糟糕，设置的越大求的均值和方差越接近整个训练集的均值和方差。
（3）一般将bn层放在卷积层（Conv）和激活层（例如Relu）之间，且卷积层不要使用偏置bias。因为使用偏置只会徒增网络的参数，导致训练起来更加的费劲。

4、为什么BN要放在卷积层和线性层后、非线性单元前？

因为非线性单元的输出分布形状会在训练过程中变化，归一化无法消除他的方差偏移，相反的，全连接和卷积层的输出一般是一个对称,非稀疏的一个分布，更加类似高斯分布，对他们进行归一化会产生更加稳定的分布。如ReLU这样的激活函数，如果你输入的数据是一个高斯分布，经过他变换出来的数据能是一个什么形状？小于0的被抑制了，也就是分布小于0的部分直接变成0了，这样不是很高斯了。

四、实验结果

1、ImageNet分类比赛

1.1、无残差网络

评估了ResNet-18和ResNet-34(均用普通残差模块构成)，下表显示了具体网络模型的构造。

​ 下表的结果显示了34层无残差网络较18层网络的验证错误率更高，原因是退化现象的存在。34层普通网络的模型容量比18层大，但训练误差始终比18层高。此时导致退化现象的不是梯度消失（因为无残差网络也要加BN层，前向、反向传播都良好）也不是过拟合问题。退化现象解释就是深度网络收敛速率会随着网络加深呈现指数级降低，这会不利于训练误差的降低，同时尝试增加迭代次数也不会使得网络退化现象变好，该问题还有待研究。

1.2、残差网络

与无残差网络结构类似，只是将短路连接加进每一组3×3卷积核上了。

​ 对所有的shortcut使用恒等映射且对于升维（下采样）时采取零填充方法，所以这相对于无残差网络不会引入额外的参数。

​ 我们在表格中有了三个重要发现：

1）退化问题在加入残差网络之后得到完美解决（层数越深、性能越好）

2）带残差效果优于不带残差的网络；

3）带残差的网络收敛速度更快。

1.3、恒等映射 VS 投影shortcut连接

在下表中对比了三种方案：

A：平常的短路连接都是恒等映射，只有升维（下采样）时采用零填充，所有的短路连接都无额外参数；

B：平常的短路连接都是恒等映射，升维时用投影短路连接，即用1×1卷积升维，但引入了额外参数；

C：所有短路连接都用1×1卷积，引入了更多的参数。

得出结论为：

①A、B、C三个方案都比不带残差的网络好；

②B比A好，因为A在升维时用padding补零相当于丢失了shortcut分支的信息，没有进行残差学习；

③C比B好，因为C的13个非下采样残差模块的shortcut都有参数，模型表示能力强；

④A、B、C都差不太多，说明恒等映射的shortcut足以解决网络退化问题，投影shortcut对于解决退化问题不是特别重要。而且C需要的参数量太大导致内存、时间复杂度较复杂，模型更大，所以综合考虑后面不用C方案。所以恒等映射可以在不增加bottleneck架构复杂度的基础上解决退化问题。

*1.4、更深的沙漏（bottleneck）结构

bottleneck结构：输入输出是高维的，中间是低维的。

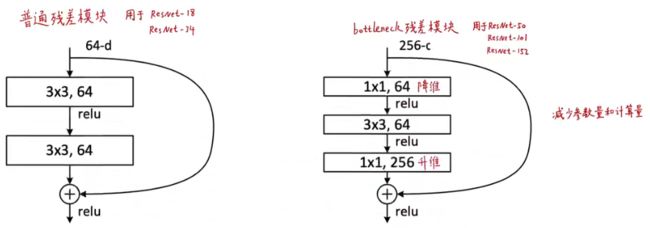
​ 考虑到训练时间成本，我们将修建块修改为bottleneck设计，对于每个残差函数F，我们都用一个三层卷积堆叠（如上面右图），三层分别为1×1（降维）、3×3（输入输出维度最小的卷积块）、1×1（升维）卷积。

​ 无参数恒等映射的shortcut对bottleneck结构非常重要，如果上右图的恒等映射shortcut变为投影映射，那么时间复杂度\计算量和模型尺寸\参数量会翻倍，因为shortcut被连接到两个高维端。所以用恒等映射的shortcut对于bottleneck结构是非常有益的。

1.5、ResNet-50、ResNet-101、ResNet-152（都用bottleneck）

ResNet-50：将ResNet-34中的双层残差快替换成了三层的bottleneck块，下采样时用方案B处理，此模型有38亿FLOPs。

ResNet-101、ResNet-152：仍然比VGG轻量化。

这三个网络的准确率都比ResNet-34要好，而且在这三个网络中也没有发现退化问题，在网络加深的同时准确率也一直在上升。

1.6、与之前先进的模型(SOTA)的对比

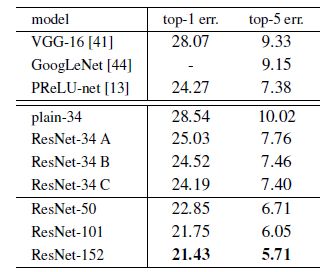
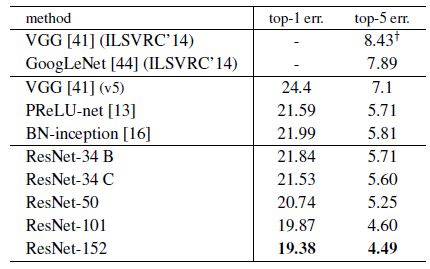
下表中我们比较了之前最好的单模型结果，ResNet-34模型已经得到了最优的准确率了，而ResNet-152的性能超过了之前所有多模型集成的结果。

我们结合了六个不同深度的模型组成了一个集成模型（在提交结果时一个集成模型只加了两个ResNet-152），但是这在ImageNet比赛上就已经拿到了当时的第一名。

2、CIFAR-10数据集

​ 在5万张训练图片和1万张测试集图片（10类别）上进行实验，在训练集上训练而在测试集上评估结果，关注重点在极深深度网络的表现上而不是刷SOTA，所以用了较简单的网络。无残差和残差网络用的是论文中图三的ResNet-34。

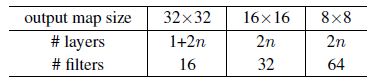
​ 网络输入为32×32图片，做去均值操作。第一层是3×3卷积，然后用3×3卷积的6n个层的堆叠分别在{32，16，8}大小的特征图上分别做卷积（即3个block在三个特征图上分别做卷积）,每个block有2n个层，卷积核数量分别为{16，32，64}。用步长为2的卷积层做下采样，网络最后再接上GAP层、10神经元的FC层和softmax。所以一共有6n+2个堆叠权重层。

​ shortcut是在每一对3×3卷积层进行连接（共有3n个短路连接），在所有case下都使用恒等映射短路连接（采用A方案），所以残差网络跟无残差网络相比有同样的深度、宽度以及参数量。

​ 训练时：设置weight decay=0.0001，momentum=0.9，He正态分布初始化，用BN层而不加Dropout，mini-batch=128，GPU number=2，learning rate=0.1(在第32000次和48000次迭代时乘以0.1)，在第64000次迭代终止，将训练集划分为45000的训练集和5000的验证集。图像增强方法为文献【24】，在每个图像上做padding=4的填充，然后在填充之后的图像上做32×32的随机裁剪或者它的水平翻转。测试时：直接用原始32×32图像进行测试。

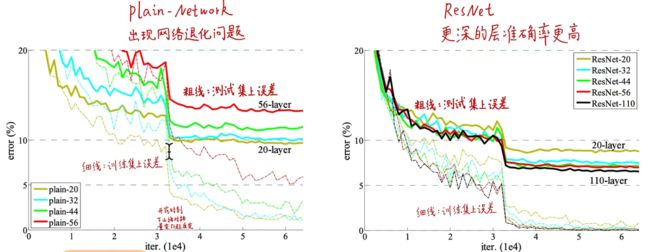
​ 分别对比了n={3,5,7,9}→层数分别对应为{20，32，44，56}的网络，下左图表现了普通网络存在着退化现象，下右图表现了加了残差模块之后网络退化现象解决。我们还尝试了n=18的110层ResNet，使用两阶段学习法：开始用小学习率预热（降低训练误差），然后再用大学习率学习，110层网络收敛效果非常好且较FitNet（用浅且宽的老师网络去训练深且窄的学生网络，即知识蒸馏）和Highway有更少的参数量。

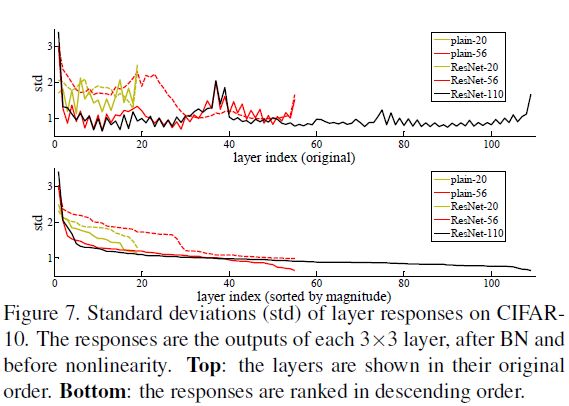
2.1、每层响应分布（每层残差层输出）分析

​ 下图1表现了每层响应的标准差，这个响应是每一层3×3卷积（在BN层之后且在ReLU等激活函数之前）的输出值。对于ResNet来说，该分析揭示了残差函数的响应强度，下图2表示残差网络输出响应较普通网络要小，且网络越深输出响应（残差）越小。

2.2、超深网络

​ 这一节开始研究超过1000层的网络，设置n=200，构造ResNet-1202，此模型没有优化困难，能收敛且没有过拟合，训练错误率低于0.1且测试错误率也较好（7.93%）。但是测试集上的性能不如ResNet-110，因为这已经过拟合了（对于这么小的一个数据集采用这么大的网络实在是没必要），所以像maxout或dropout这样的方式是要被采用的。在本文中我们没有使用maxout\dropout而只是设计了深而窄的网络结构来进行简单的正则化。但是结合更强的正则化可能会改善结果，在未来研究这些。

总结

1、退化现象

定义：随着网络深度的增加，准确率开始达到饱和并且在之后会迅速下降。

判断方法：随着网络的加深，错误率不降反升，收敛速率也呈指数级下降。

原因：网络过于复杂，训练不加约束。

解决方案：使用残差网络结构。

2、在残差网络中得出的结论为：①极深残差网络易于优化收敛；②解决了退化问题；③可以在很深的同时提升准确率。

3、网络构造选用步长为2的卷积核进行下采样，最后是一个GAP层和一个1000个神经元的带有softmax的FC层。其余大部分遵照VGGNet的设计原则。

4、本文提出两种残差结构，一种是两层卷积残差块，应用于ResNet-18和ResNet-34；另一种是bottleneck三层卷积残差块(分别为1×1降维、3×3、1×1升维)，应用于ResNet-50、ResNet-101和ResNet-152。ResNet-50、ResNet-101、ResNet-152性能都比ResNet-34好。

5、升维（下采样）时有三种方案供选择，但是优先选择B方案（通过1×1卷积匹配维度）

6、无参数恒等映射的shortcut对bottleneck结构非常重要。

ResNet代码实现（pytorch）

import torch
import torch.nn as nn
import torch.nn.functional as F

# 用于ResNet-18和ResNet-34的残差块，用的是2个3x3的卷积
class BasicBlock(nn.Module):
    expansion = 1

    def __init__(self, in_planes, planes, stride=1):
        super(BasicBlock, self).__init__()
        self.conv1 = nn.Conv2d(in_planes, planes, kernel_size=3, stride=stride, padding=1, bias=False)
        self.bn1 = nn.BatchNorm2d(planes)
        self.conv2 = nn.Conv2d(planes, planes, kernel_size=3, stride=1, padding=1, bias=False)
        self.bn2 = nn.BatchNorm2d(planes)
        self.shortcut = nn.Sequential()
        # 经过处理后的x要与x的维度相同(尺寸和深度)
        # 如果不相同，需要添加1×1卷积+BN来变换为同一维度
        if stride != 1 or in_planes != self.expansion * planes:
            self.shortcut = nn.Sequential(nn.Conv2d(in_planes, self.expansion * planes, kernel_size=1, stride=stride, bias=False),
                                          nn.BatchNorm2d(self.expansion * planes))

    def forward(self, x):
        out = F.relu(self.bn1(self.conv1(x)))
        out = self.bn2(self.conv2(out))
        out += self.shortcut(x)
        out = F.relu(out)
        return out


# 用于ResNet-50,ResNet-101和ResNet-152的残差块，用的是1x1+3x3+1x1的卷积
class Bottleneck(nn.Module):
    # 前面1x1和3x3卷积的filter个数相等，最后1x1卷积是其expansion倍
    expansion = 4

    def __init__(self, in_planes, planes, stride=1):
        super(Bottleneck, self).__init__()
        self.conv1 = nn.Conv2d(in_planes, planes, kernel_size=1, bias=False)
        self.bn1 = nn.BatchNorm2d(planes)
        self.conv2 = nn.Conv2d(planes, planes, kernel_size=3, stride=stride, padding=1, bias=False)
        self.bn2 = nn.BatchNorm2d(planes)
        self.conv3 = nn.Conv2d(planes, self.expansion * planes, kernel_size=1, bias=False)
        self.bn3 = nn.BatchNorm2d(self.expansion * planes)
        self.shortcut = nn.Sequential()
        if stride != 1 or in_planes != self.expansion * planes:
            self.shortcut = nn.Sequential(nn.Conv2d(in_planes, self.expansion * planes, kernel_size=1, stride=stride, bias=False),
                                          nn.BatchNorm2d(self.expansion * planes))

    def forward(self, x):
        out = F.relu(self.bn1(self.conv1(x)))
        out = F.relu(self.bn2(self.conv2(out)))
        out = self.bn3(self.conv3(out))
        out += self.shortcut(x)
        out = F.relu(out)
        return out


class ResNet(nn.Module):
    def __init__(self, block, num_blocks, num_classes=10):
        super(ResNet, self).__init__()
        self.in_planes = 64

        self.conv1 = nn.Conv2d(3, 64, kernel_size=3, stride=1, padding=1, bias=False)
        self.bn1 = nn.BatchNorm2d(64)

        self.layer1 = self._make_layer(block, 64, num_blocks[0], stride=1)
        self.layer2 = self._make_layer(block, 128, num_blocks[1], stride=2)
        self.layer3 = self._make_layer(block, 256, num_blocks[2], stride=2)
        self.layer4 = self._make_layer(block, 512, num_blocks[3], stride=2)
        self.linear = nn.Linear(512 * block.expansion, num_classes)

    def _make_layer(self, block, planes, num_blocks, stride):
        strides = [stride] + [1] * (num_blocks - 1)
        layers = []
        for stride in strides:
            layers.append(block(self.in_planes, planes, stride))
            self.in_planes = planes * block.expansion
        return nn.Sequential(*layers)

    def forward(self, x):
        out = F.relu(self.bn1(self.conv1(x)))
        out = self.layer1(out)
        out = self.layer2(out)
        out = self.layer3(out)
        out = self.layer4(out)
        out = F.avg_pool2d(out, 4)
        out = out.view(out.size(0), -1)
        out = self.linear(out)
        return out


def ResNet18():
    return ResNet(BasicBlock, [2, 2, 2, 2])


def ResNet34():
    return ResNet(BasicBlock, [3, 4, 6, 3])


def ResNet50():
    return ResNet(Bottleneck, [3, 4, 6, 3])


def ResNet101():
    return ResNet(Bottleneck, [3, 4, 23, 3])


def ResNet152():
    return ResNet(Bottleneck, [3, 8, 36, 3])

引用

[1] 【精读AI论文】ResNet深度残差网络_哔哩哔哩_bilibili

[2] 一文搞懂BN的原理及其实现过程（Batch Normalization）_jhsignal的博客-CSDN博客_bn模型

[3] BN层原理解析_朗云星空-CSDN博客_bn层

[4] pytorch实现ResNet_winycg的博客-CSDN博客_pytorch resnet