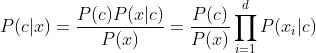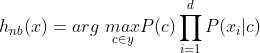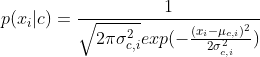机器学习算法——贝叶斯分类器3（朴素贝叶斯分类器）

基于贝叶斯公式来估计后验概率P(c|x)的主要困难在于：类条件概率P(x|c)是所有属性上的联合概率，难以从有限的训练样本直接估计而得。

为避开这个障碍，朴素贝叶斯分类器（Naive Bayes classfier）采用了“属性条件独立性假设”：对已知类别，假设所有属性相互独立。换句话说，每个属性独立地对分类结果产生影响。

基于属性条件独立性假设，可重写P(c|x)

其中，d为属性数目，为x在第i个属性上的取值。由于对所有类别来说P(x)相同，则贝叶斯判定准则为(即朴素贝叶斯分类器的表达式)：

显而易见，朴素贝叶斯分类器的训练过程就是基于训练集D来估计类先验概率P(c)，并为每个属性估计条件概率P(Xi|c)。

令表示训练集D中第c类样本组成的集合，若有充足的独立同分布样本，则可容易地估计出类先验概率：

对离散属性而言，令表示中在第i个属性上取值为的样本组成的集合，则条件概率可估计为

对连续属性可考虑概率密度函数，假定,其中和分别是第c类样本在第i个属性上取值的均值和方差，则有

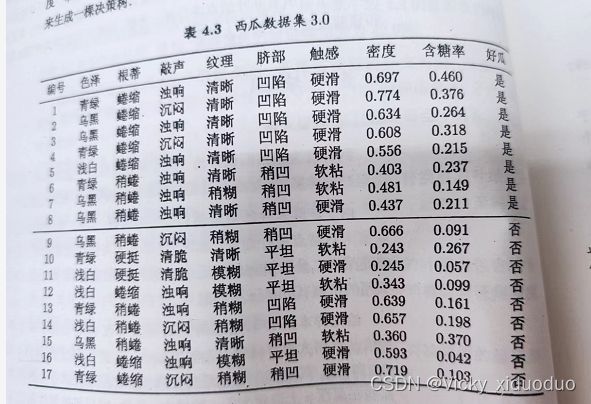
用西瓜数据集来实例讲解朴素贝叶斯分类器。

给定测试样本1

对上述进行分类，看是好瓜还是坏瓜？

首选估计类先验概率P(c),显然有

P(好瓜=是)=≈0.471

P(好瓜=否)=≈0.529

然后为每个属性估计条件概率 

 P(色泽=青绿|好瓜=是) = 3/8 =0.375

 P(色泽=青绿|好瓜=否) = 3/9 ≈ 0.333

P(根蒂=蜷缩|好瓜=是) = 5/8 = 0.375

P(根蒂=蜷缩|好瓜=否) = 3/9 ≈ 0.333

P(敲声=浊响|好瓜=是)= 6/8 = 0.75

P(敲声=浊响|好瓜=否) = 4/9 ≈ 0.444

P(纹理=清晰|好瓜=是)= 7/8 = 0.875

P(纹理=清晰|好瓜=否) = 2/9 ≈ 0.222

P(脐部=凹陷|好瓜=是)= 5/8 = 0.625

P(脐部=凹陷|好瓜=否) = 2/9 ≈ 0.222

P(触感=硬滑|好瓜=是)= 6/8 = 0.75

P(触感=硬滑|好瓜=否) = 6/9 ≈ 0.667

P(密度=0.697|好瓜=是)【带入正态分布概率公式】≈ 1.959

P(密度=0.697|好瓜=否)【带入正态分布概率公式】≈ 1.203

 P(含糖率=0.46|好瓜=是)【带入正态分布概率公式】≈ 0.788

P(含糖率=0.46|好瓜=否)【带入正态分布概率公式】≈ 0.066

P(好瓜=是)× P(色泽=青绿|好瓜=是)×P(根蒂=蜷缩|好瓜=是)×P(敲声=浊响|好瓜=是)×P(纹理=清晰|好瓜=是)×P(脐部=凹陷|好瓜=是)×P(触感=硬滑|好瓜=是)×P(密度=0.697|好瓜=是)×P(含糖率=0.46|好瓜=是)≈0.031

P(好瓜=否)× P(色泽=青绿|好瓜=否)×P(根蒂=蜷缩|好瓜=否)×P(敲声=浊响|好瓜=否)×P(纹理=清晰|好瓜=否)×P(脐部=凹陷|好瓜=否)×P(触感=硬滑|好瓜=否)×P(密度=0.697|好瓜=否)×P(含糖率=0.46|好瓜=否) ≈6.8 ×

由于，因此将朴素贝叶斯分类器将测试样本1判别为好瓜。

需要注意一点：若某个属性值在训练集中没有与某个类同时出现过，则直接进行概率估计进行判别分类会出现问题，例如，对一个“敲声=清脆”的测试例，有P(敲声=清脆|好瓜=是)=0/8=0.因此，无论该样本的其他属性是什么，哪怕在其它属性上明显是好瓜，分类的结果都将是“好瓜=否”,这显然不合理。

为了避免其它属性携带的信息被训练集中未出现的属性值“抹去”，在估计概率值时通常要进行平滑。常用拉普拉斯修正。

令N表示训练集D中可能的类别数，表示第i个属性可能的取值数。则P(c)和P(xi|c)可修正为：

例如，本节的例子中，类先验概率可估计为：

(好瓜=是)=9/（17+2）≈ 0.474

（好瓜=否）=10/（17+2） ≈ 0.526

(色泽=青绿|好瓜=是) = （3+1） / （8+3）≈ 0.364等等

上文提到的P(敲声=清脆|好瓜=是)= （0+1）/（8+3）≈ 0.091。

 朴素贝叶斯分类器有多种使用方式；

1. 若任务对预测速度要求高，则对给定训练集，可将贝叶斯分类器涉及的所有概率估值计算出来并存入表中，这样进行预测时，直接查表就能进行判别；

2. 若任务数据更换频繁，则可采用懒惰学习，先不进行任何训练，待收到预测请求时再根据当前数据集进行概率估值。

3. 若数据不断增加，则可在现有估值的基础上，仅对新增加的样本属性值所涉及的概率估值进行计数修正即可，实现增量学习。

除了朴素贝叶斯分类器外，还有半朴素贝叶斯分类器，将在下节中进行讲解。