Model-Agnostic Meta-Learning for Fast Adaptation of Deep Networks阅读笔记

Abstract

       本文是针对meta-learning提供了一种模型无关的，适用于任何使用梯度下降 的方式来训练模型的算法，可以应用于各种学习问题：分类、回归、强化学习。
       元学习(meta-learning)的目标： 通过对不同的任务进行训练，以至于在新的学习任务上只需要使用很少的训练样本，就能达到较好的性能。这篇文章提出的MAML对于训练出来的模型，通过微调就能在新任务上达到较好的性能。
       关键思想： 训练模型的初始化参数，使得模型在新的任务上使用很少的样本，进行一次或几次梯度下降就可以取得最大化的表现。
模型的特点（优点）：

1. MAML 不会大量增加学习的参数（其实理论上只增加一个参数 – 元学习率）
2. MAML 不会对模型进行任何限制，只限制训练的方法是梯度下降，其实很大部分情况都满足这个条件
3. MAML 可以用于大量的损失函数，比如可微的监督损失，不可微的强化学习目标。

文章的贡献：

1. 一个简单的模型无关的任务无关的算法用于元学习训练模型的参数，使得少量的梯度更新可以使模型在新任务上快速学习。
2. 在不同的任务：少样本图片分类，少样本回归和策略梯度强化学习上对算法进行了验证。
3. 实验证明算法可以和专门用于少样本图片分类的方法一样取得 state of the art 的结果，并且使用了更少的参数，还易于用于回归问题强化学习等问题。

MAML算法

       在few-shot learning中有个术语叫做N-way K-shot问题，意思就是训练集中有N个类别，每个类别K个样本，即要求模型通过N*K个样本学会分辨这N个类别。
       在 Meta-learning 中之前学习的 task 我们称为 meta-training task，我们遇到的新的 task（包含新的类）称为 meta-testing task。因为每一个 task 都有自己的训练集和测试集，因此为了不引起混淆，我们把 task 内部的训练集和测试集一般称为 Support set 和 Query set。

问题设置

我们考虑一个模型表示为$f$，他将观测值x映射到输出a。在元学习过程中，模型被训练成能够适应大量或无限数量的任务。任务可以形式化的定义为T={L(x1，a1，…，xH，aH)，q(x1)，q(xt+1|xt，at)，H}，由损失函数L(x1就是样本，a1就是样本的预测结果，通过x1和a1计算损失)、初始观测值的分布q(x1)(也就是样本x的分布)、迁移分布q(xt+1|xt，at)和任务长度H组成。该模型可以通过在每个时间t处选择输出来生成长度为H的样本。 损失L(x1，a1，…，xH，aH)→$\mathbb{R}$提供特定于任务的反馈，一般是误分类的损失或者代价函数。

       大致训练过程： 在我们的元学习场景中，我们考虑我们希望我们的模型能够适应的任务p(T)的分布。在K-shot学习设置中，模型被训练为仅从qi提取的K个样本和由Ti生成的反馈LTi中学习从p(T)提取的新任务Ti。在元训练过程中，从p(T)中采样一个任务Ti，用K个样本和来自Ti的相应损失LTi的反馈来训练模型，然后在Ti的新样本上进行测试。然后通过考虑qi新数据的测试误差相对于参数的变化来改进模型f。实际上，采样任务T1上的测试误差充当元学习过程的训练误差。元训练结束时，从p(T)中抽取新的任务，通过模型从K个样本中学习后的表现来衡量元表现。通常，用于元测试的任务在元训练期间进行。

MAML算法

       不同于其他方法，例如有的方法训练一个循环神经网络(RNN)来吸收整个数据集(概述博客中的基于 RNN 记忆的方法)或者结合无参数的特征 embedding 的方法(度量学习),MAML 使用元学习的学习机制学习一个好的初始化参数，对于新的任务能进行快速适应。
       我们对这个问题采取了一种明确的方法：在新任务上使用基于梯度下降的fine-tune的方式去训练模型，因此我们将以这样的方式学习一个模型：这种基于梯度的学习规则可以在从p（T）提取的新任务上快速进行，而不会过度拟合.
       我们的目标：找到模型的参数，使模型的参数对于任务的改变是敏感的，这样参数上的小的改变可以给新任务的损失带来巨大的改进。
       形式化来说，我们使用$f_{\theta }$来表示模型，参数为$\theta$。对于某一个任务(meta-training task)${\tau }_i$，模型的参数使用梯度下降变为${\theta }^{\prime }$，其中梯度下降的次数为一次或者多次。文章中为了简洁，使用一次梯度进行表示：

${\theta }_i^{\prime }=\theta -\alpha {▽}_{\theta }{L}_{{\tau }_i}(f_{\theta })$ （1）

其中$\alpha$是学习步长，也叫任务学习率(task learning rate)，可以是一个超参数，也可以是一个学习来的参数。$L_{{\tau }_i}(f_{\theta })$是使用参数$\theta$在任务${\tau }_i$上的损失函数，${▽}_{\theta }{L}_{{\tau }_i}(f_{\theta })$是损失函数相对于参数$\theta$的梯度。
       上面的计算过程只是在一个任务上更新了参数${\theta }^{\prime }$，但是我们的想法是：训练模型的初始化参数，使得模型在新的任务上使用很少的样本，进行一次或几次梯度下降就可以取得最大化的表现。学习的初始化参数（内在特征表示）应该适用于大量的各种的任务，而不是单单某一个任务。

所以模型参数$\theta$的更新为：

$\theta \leftarrow \theta -\beta {▽}_{\theta }{\sum }_{{\tau }_i\sim p({\tau }_i)}{L}_{{\tau }_i}(f_{{\theta }_i^{\prime }})$ (2)

其中$\beta$叫元学习步长，也叫元学习率(meta-learning rate)。$p(\tau )$是meta-learning tasks的任务分布，其实就是在 meta-training tasks 采样出 task 来 meta-training，因为一次可以采样多个，所以有一个求和。下面是一个简单的参数示意图帮助大家理解其训练的过程：

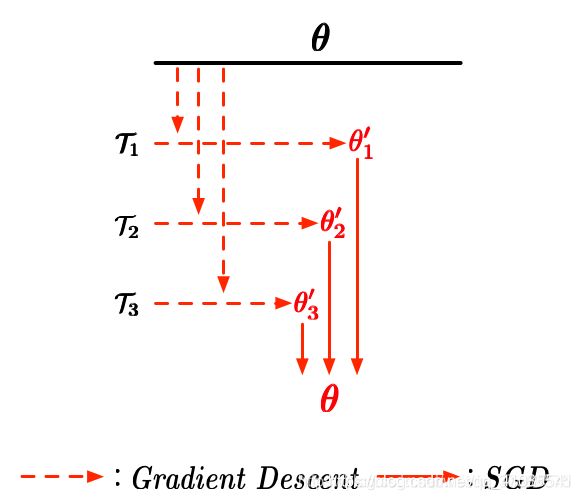
比如我们一次学习 3 个任务，然后用最开始的参数参数 $\theta$ 分别在这三个任务上 ${\tau }_1,{\tau }_2,{\tau }_3$ 上进行梯度下

${\theta }_i^{\prime }=\theta -\alpha {▽}_{\theta }{L}_{{\tau }_i}(f_{\theta })$

得到分别对应3个任务的参数${\theta }_1^{\prime },{\theta }_2^{\prime },{\theta }_3^{\prime }$，然后使用

$\theta \leftarrow \theta -\beta {▽}_{\theta }{\sum }_{{\tau }_i\sim p({\tau }_i)}{L}_{{\tau }_i}(f_{{\theta }_i^{\prime }})$

进行梯度的更新，得到新一轮的初始化参数 $\theta$，反复进行很多次，最终 meta-training 的结果就是初始化参数$\theta$。在面对新的任务的时候，我们还需要对 $\theta$ 进行一次或几次的梯度更新：

${\theta }_i^{\prime }=\theta -\alpha {▽}_{\theta }{L}_{{\tau }_i}(f_{\theta })$

Require：$p(\tau )$：任务的分布
Requore: $\alpha ,\beta$：超参数

1. 随机初始化参数$\theta$
2. 循环（相当于所有的batch集合，也就是在整个训练集上）
3. 从任务分布$p(\tau )$上采样1个batch作为${\tau }_i$
4. for循环，对这个batch上的所有task执行以下过程
5. 计算每个task上K个样本的损失函数的梯度${▽}_{\theta }{L}_{{\tau }_i}(f_{\theta })$
6. 使用梯度更新来更新每个任务的参数${\theta }^{\prime }$, 也就是${\theta }_i^{\prime }=\theta -\alpha {▽}_{\theta }{L}_{{\tau }_i}(f_{\theta })$
7. for循环结束
8. 通过这一个batch中tasks的损失之和来更新参数$\theta$(也就是通过每个task的参数${\theta }_1^{\prime },{\theta }_2^{\prime },{\theta }_3^{\prime }$更新参数) $\theta \leftarrow \theta -\beta {▽}_{\theta }{\sum }_{{\tau }_i\sim p({\tau }_i)}{L}_{{\tau }_i}(f_{{\theta }_i^{\prime }})$
9. 结束循环

       实际上，模型的参数更新过程可以概括为：首先使用初始化的参数$\theta$在某个任务上计算损失函数，通过梯度下降更新为${\theta }^{\prime }$，然后在使用更新后的新参数${\theta }^{\prime }$计算一下损失，看看是不是几步梯度下降了是不是改善了效果：这就是${▽}_{\theta }{\sum }_{{\tau }_i\sim p({\tau }_i)}{L}_{{\tau }_i}(f_{{\theta }_i^{\prime }})$ 这一部分的直觉表述，然后我们知道了这个初始化参数 $\theta$ 需要如何调整，使得可以在遇到新的任务上几步梯度下降就可以很大地改善了效果。这就是公式 2 的直觉表达。这样多次执行，我们的初始化参数 $\theta$ 被反复激励，最后真的可以在新的任务上几步梯度下降就可以很大地改善了效果。
       我们一定要记住：我们无论是学习过程中，还是最后 meta-training 完了之后 $\theta$ 都是相对于任务的初始化参数，它是适合于大量的任务，但是对于某一个确定的任务，还需要进行微调。我们 meta-testing 的时候，要用新任务上的少量的样本使用公式 1 进行梯度下降，得到${\theta }^{\prime }$ ，这才是我们用来测试学习新任务学习情况的参数。所以 MAML 被我在概述中分类为学习微调(learning to fine-tuning)中去。

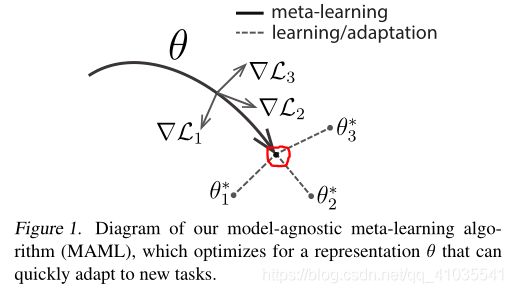
       这张图描述了MAML想要寻找的参数$\theta$的位置，首先在训练的task上计算每个task的loss，然后把一个batch中所有的task(多个task)求和作为Loss再进行优化，这个过程结束后，参数$\theta$到达图中的红色点。在这个点上可以快速适应新的任务。

MAML vs Pre-training

       MAML和Pre-training两个概念其实非常相似，Meta Learning对应Pretraining, 而Adaption对应Fine-Tune。但是，Meta Learning其范式的，在目标上和Pretraining有着实质的区别。这种区别从其Loss上看得很明白。
       Pre-training(预训练)： 你需要搭建一个网络模型来完成一个特定的图像分类的任务。首先，你需要随机初始化参数，然后开始训练网络，不断调整直到网络的损失越来越小。在训练的过程中，一开始初始化的参数会不断变化。当你觉得结果很满意的时候，你就可以将训练模型的参数保存下来，以便训练好的模型可以在下次执行类似任务时获得较好的结果。这个过程就是 pre-training。
       fine tune(微调)： 之后，你又接收到一个类似的图像分类的任务。这时候，你可以直接使用之前保存下来的模型的参数来作为这一任务的初始化参数，然后在训练的过程中，依据结果不断进行一些修改。这时候，你使用的就是一个 pre-trained 模型，而过程就是 fine tuning。
       MAML(模型无关的元学习)： 训练模型的初始化参数，使得模型在新的任务上使用很少的样本，进行一次或几次梯度下降就可以取得最大化的表现。也就是说对于模型的参数，在新任务上需要进行几次的梯度更新，然后用于测试任务。
MAML的损失函数：

$L(\varphi )={\sum }_{i=1}^N{l}^n({\hat{\theta }}^n)$

Model Pre-training的损失函数：

$L(\varphi )={\sum }_{i=1}^N{l}^n(\varphi )$

其中$\varphi$是初始化参数(可以理解为预训练得到的参数)，${\hat{\theta }}^n$就是模型从task_n学习后的参数，$l^n({\hat{\theta }}^n)$代表task_n上的损失。从这里我们可以看出，MAML中Loss中每个任务的$l^n({\hat{\theta }}^n)$是用$\varphi$训练完后的参数$\hat{\theta }$计算的；而Pre-training是通过对每个任务对当前的$\varphi$计算出来的。

       MAML： 使用MAML时，我们并不在意$\varphi$在这些训练任务上表现如何，我们在意的是经过训练以后的表现。比如下图中的$\varphi$在当前的task_1和task_2上表现不是很好，但是把这个位置的$\varphi$当做初始的参数，但是经过训练后的${\hat{\theta }}^1,{\hat{\theta }}^2$可以达到极值点，也就是最好的参数。

       Model Pre-training: Model Pre-training在意的是现在的$\varphi$的表现如何，比如下图中的$\varphi$同时在当前的task_1和task_2上都表现的很好，但是并不保证用$\varphi$去训练以后能得到很好的${\hat{\theta }}^n$。

       所以来说，MAML找的$\varphi$是经过训练之后变现很好(看的是潜力)，而Model Pro-training找的$\varphi$是现在表现的很好。 打个比方，你毕业以后到底做什么好，是继续读博(读完博之后道路就更加宽广, MAML)，还是直接工作(马上可以赚钱，Model Pro-training)
MAML在实际操作的时候，在训练时假设就只update一次，在测试时可以update多次。

下面通过两个图示来进一步说明MAML和Model Pro_training的区别：

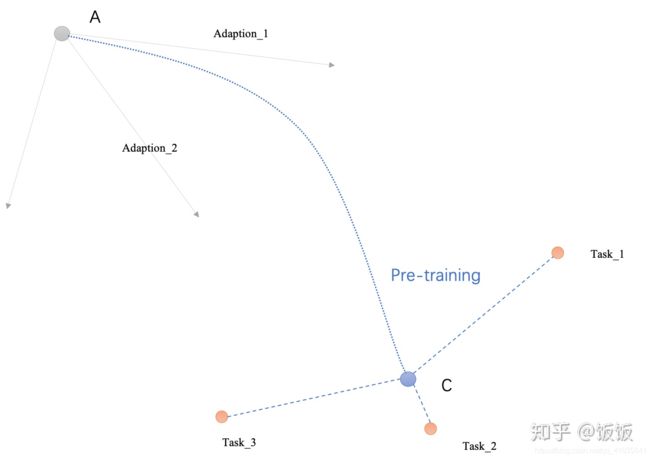
对于普通的Pre-training，Adaption是完全不考虑的，他只会找到离task1,task2,task3都距离最近的那个点。但这个点不能保证在做完Adaption1,Adaption2,Adaption3之后，他们各自能离最佳点最近。

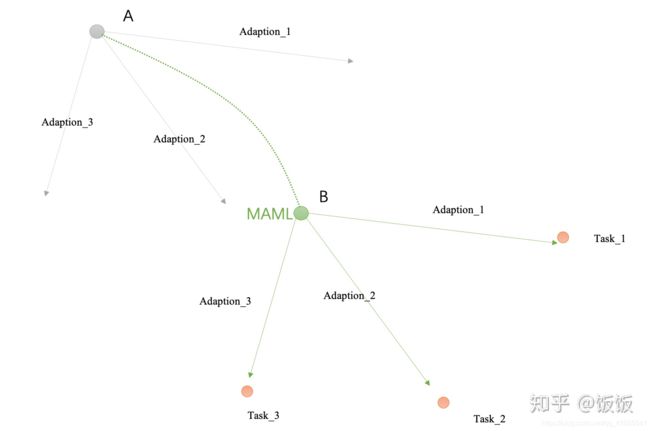
在Meta Learning(MAML)的过程中，优化器带着原点以及Adaption1，Adaption2,Adaption3三条线一起移动，他的目标是找到一个位置，使得Adaption1，Adaption2,Adaption3三条线的末端刚好离task1,task2,task3最近

       然而这些是理论。实际使用MAML很多人应该发现， MAML效果在大多数情况下并没有过于神奇。而且实际看来，MAML的最佳点往往离Pretraining的最佳点并没有那么大不同。也就是二者实际效果还是相当一致的。当然，我们可以找出一些case， 实际MAML的最佳点和Pretraining的最佳点相隔很远。但是这些都比较trick。

梯度求解

       对于每个任务task，参数更新使用这个式子:

$\hat{\theta }=\varphi -\epsilon {▽}_{\varphi }l(\varphi )$ (3)

对于一个batch(多个任务的集合)，参数更新的式子为:

$\varphi \leftarrow \varphi -\eta {▽}_{\varphi }L(\varphi )$ (4)

其中，$L(\varphi )={\sum }_{i=1}^N{l}^n({\hat{\theta }}^n)$ (5)。通过(3)、（4）、（5）可以得到：

${▽}_{\varphi }L(\varphi )={▽}_{\varphi }{\sum }_{n=1}^N{l}^n(\widehat{{\theta }^n})={\sum }_{n=1}^N{▽}_{\varphi }{l}^n(\widehat{{\theta }^n})$

Real Implementation：

两者的区别：
1. MAML
       其中${\varphi }^0$是初始值$\varphi$的初始值，假设一个batch只选择一个task。首先在task_m上训练得到参数${\hat{\varphi }}^m$，然后在进行一次更新(batch的更新)，更新后的参数就变为${\varphi }^1$；同样，第二个batch上只有一个task_n，所以现在tak_n上更新参数得到${\hat{\varphi }}^n$，然后在进行batch的更新，得到参数${\varphi }^2$ 。
2. Model Pre-training
       首先在task_m上进行更新，得到参数${\hat{\theta }}^m$，然后沿着这个方向，将$\varphi$更新为${\varphi }^1$；然后在task_n上进行参数更新，得到参数${\hat{\varphi }}^n$，然后沿着这个方向将$\varphi$更新为${\varphi }^2$。
Model Pro-training就是看当前每个task计算的梯度是那个方向，$\varphi$就往那个方向更新； MAML是走两步梯度，然后使用第二步的梯度进行初始化参数$\varphi$的更新。

其他部分

论文中的实验、结论等相关部分请参考原论文。

参考链接：
论文原文链接
论文翻译Model-Agnostic Meta-Learning for Fast Adaptation of Deep Networks
MAML: Model-Agnostic Meta-Learning for Fast Adaptation of Deep Networks笔记
论文阅读：Model-Agnostic Meta-Learning for Fast Adaptation of Deep Networks
预训练与微调
MAML和pretraining的有本质区别吗？
李宏毅老师对MAML的讲解