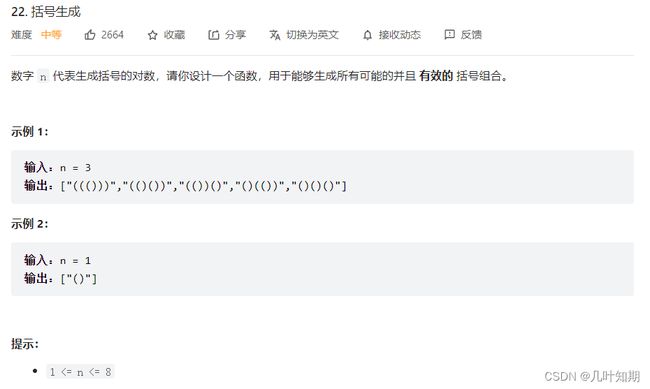
【程序员日记2022-5-27】LeetCode.22 回溯总结

今天因为看了恋爱综艺，有点上头，所以学习的时间没多少（苦恼ing），综艺是b站的《90婚介所》，恋爱，果然还是看别人谈比较有意思哈哈哈。作为一名合格的研究生，我也是十点钟就早早的来到实验室开始了一天的打工生活，上午写了一道算法题，LeetCode22.括号生成。这一写就是一上午啊…不过收获挺大，因为把之前比较模糊的知识点，认真的总结了一下。

话不多说，直接上题解。

本题呢，也是用到了深度优先遍历（DFS），早就浅学习过优先遍历和广度优先遍历（BFS）了，但是印象总是比较模糊，今天就仔细总结一下，彻底的理解透这两个概念。（参考文章）

1.深度优先遍历和广度优先遍历

所谓的深度优先遍历，主要思路是从图中一个未访问的顶点 V 开始，沿着一条路一直走到底，然后从这条路尽头的节点回退到上一个节点，再从另一条路开始走到底…，不断递归重复此过程，直到所有的顶点都遍历完成，它的特点是不撞南墙不回头，先走完一条路，再换一条路继续走。如果类比到学过的二叉树，实际上就是前序遍历，如果是多叉树，那就是依次走完从根节点到叶子节点的所有路径，可以通过递归来实现。

所谓的广度优先遍历，指的是从图的一个未遍历的节点出发，先遍历这个节点的相邻节点，再依次遍历每个相邻节点的相邻节点。类比二叉树，实际上就是层序遍历，一般要借助栈来实现。

2.判断有效括号的条件

本题是求组合，一般求集合、组合类的题目，可以枚举出所有的情况，再选出符合条件的记录下来即可。但是要想解决本题，要想到符合有效括号的条件，这个我自己也想不到，只能通过做题来积累这些思维吧。

条件一：在括号字符中，所有的前缀字符都要满足左括号的数量要大于右括号的数量。

例如：（（（）这种情况后面再添加右括号是有可能是有效的；但是（）））（（这种一旦有前缀子串右括号数量大于左括号数量，后面怎么添加都是无效的，举个极端情况 ）（（ 一旦第一个是右括号，就不可能满足条件一了。

条件二：左括号数量等于右括号数量。这个很好理解，就不作解释了。

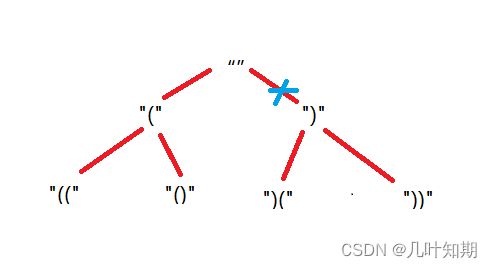
如图所示，问题就成了一个遍历的过程，一开始字符串是空的，每次可以添加左括号和右括号，知道满足要添加的括号的数量为止。涉及到遍历，那就可以用深度优先遍历和广度优先遍历了，我还是比较喜欢用深度优先遍历，毕竟可以递归实现。

3.暴力全遍历

接下来给出两种解法，第一种是纯暴力的思路，列举出所有的情况，然后选择符合题目条件的组合即可。虽然这样不好，但我还是实现了一遍，因为它能帮助我更好的理解递归和回溯的过程，还有判断符号是否有效的过程。

说明：以下代码中，path是用来保存括号字符串，就是经过每个节点的情况，res用来保存所以满足条件的括号字符串。

bool isValid(const string& str)
{
    /* 判断这个括号字符串是否合法有两个条件
    1.左括号数等于右括号数
    2.前缀里左括号数要小于等于右括号数
    */
    int balance = 0;
    for(int i=0;i& res,int n)
{
    /* 
    就暴力遍历所有的情况呗，看到有符合条件的就插入
    */
   
   if(path.size()>=2*n){
       if(isValid(path) && path.size()==2*n) res.push_back(path);
       return;
   }

   path.push_back('('); // 处理
   backtrcacing(path,res,n);//递归
   path.pop_back(); //回溯撤销处理

   path.push_back(')');
   backtrcacing(path,res,n);
   path.pop_back();

}

这里用到了递归和回溯处理，在这里做个小结，也是自己的理解。首先，递归的终止条件是根据题目的要求而定的，比如本题的终止条件就是，括号的数量达到了要求的数量，而保存结果，需要满足符号有效才行。

递归呢，如果以二叉树为例，那就是前序遍历（DFS），递归深度一直到达，最深的左子树节点，然后返回。这里的返回就是一个回溯的过程，就是搜索的路径不满足条件了，需要回到上一层节点，在继续尝试其他路径（右子树）。如果递归之前做了处理，比如加了左括号，原来是（ 变成（（ ，那么回溯到本层的时候，就要把这个处理撤销掉，由（（变成（ ，然后尝试其他路径又是一种新的情况，比如从（ 往右走变成（）。在多叉树里也是同理，而且用多叉树的深度优先遍历来枚举不同的组合，往往更常见。

4.剪枝优化遍历

方法二，其实就是做了剪枝优化，不必要的情况，不用去搜索遍历了。比如不满足条件一和条件二的情况就不用搜索了，这样可以大大降低时间复杂度。

/* 
全搜索会做很多无用功，可以适当剪枝
可以记录左右括号的数量，保证前缀里，左括号数量大于右括号的数量，并且左括号数量要小于n
 */

void cut_serach(string& path,vector& res,int n,int left,int right)
{
    if(path.size()==2*n){
        res.push_back(path);
        return;
    }

    //满足条件二，左括号数量一定是一半
    if(left

5.总结

因为之前刷过代码随想录，所以把回溯的框架再复习一下

//多叉树回溯框架
void backtracing(参数){
    if(终止条件){
        保存路径结果;
        return;
    }
    for(遍历多叉树该层的所有节点){
        处理;
        backtracing(参数);//回溯
        撤销处理;
    }
}

在回溯函数的传参中，传值和传引用会有很大的区别！！以string类型为例，如果是传值传参，那么递归到下一层时，会进行深拷贝！就是新开辟一个空间，复制一份原来string的内容过来，传参是把拷贝内容传递下去。这样传参优点就是，下一层的操作不影响上一层，在回溯函数里，不用做撤销处理。但是缺点也非常的明显，那就是每次递归，都会进行string的深拷贝，如果string占用内存很大，递归层次很多的话，这样对内存的消耗是不可想象的，所以作为一名优秀的程序员，绝对不能图代码上的简洁而使用值拷贝！！

操作不影响上一层，在回溯函数里，不用做撤销处理。但是缺点也非常的明显，那就是每次递归，都会进行string的深拷贝，如果string占用内存很大，递归层次很多的话，这样对内存的消耗是不可想象的，所以作为一名优秀的程序员，绝对不能图代码上的简洁而使用值拷贝！！

如果是传引用，那么久不会存在这样的问题了，每次的传参和使用，都在同一个string上进行操作，因此在回溯的时候，想要返回到每一层时，都保持原有状态的话，就要进行撤销处理，这也是回溯的一个精髓所在吧。