Spectrally Normalized Generative Adversarial Networks (SN-GAN)谱归一化在GAN中的运用。
《Spectral Normalization for Generative Adversarial Networks》是Takeru Miyato在2018年发表的一篇将谱理论应用于GAN的论文。
SN-GAN将鉴别器中的权重矩阵归一化为对应的谱范数,有助于控制鉴别器的Lipschitz常数。说明了参数矩阵的谱范数对多层神经网络泛化的影响。
利普希茨连续(Lipschitz连续),要求函数图像的曲线上任意两点连线的斜率一致有界,就是任意的斜率都小于同一个常数,这个常数就是Lipschitz常数。Lipschitz条件限制了函数变化的剧烈程度,即函数的梯度。因此函数更加平滑,在神经网络的优化过程中,参数变化也会更稳定,不容易出现梯度爆炸。
在 GAN 中,假设我们有一个判别器 D: I→R,其中 I 是图像空间。如果判别器是 K-Lipschitz continuous 的,那么对图像空间中的任意 x 和 y。
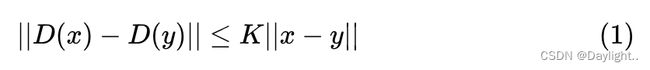 其中 || · || 为 L2 norm,如果 K 取到最小值,那么 K 被称为 Lipschitz constant。
其中 || · || 为 L2 norm,如果 K 取到最小值,那么 K 被称为 Lipschitz constant。
《Wasserstein GAN》中,对GAN提出了一种新的Loss定义Wasserstein Distance距离取代之前的 KL 散度或者 JS 散度,作为 GAN 判别器的损失函数:
 其中 Pr 和 Pg 分别为真实数据和生成数据的分布函数,Wasserstein 距离衡量了这两个分布函数的差异性。根据两个分布函数分别生成一堆数据 x1, x2, … , xn 和 y1, y2, … , yn,然后计算数据之间的距离。距离的算法是找到一种一一对应的配对方案 γ~∏(Pr, Pg),把 xi 移动到 yj,求总移动距离的最小值。Pr 和 Pg 都没有显式的表达式,只能是从里面不停地采样,所以不可能找到这样的 γ。
其中 Pr 和 Pg 分别为真实数据和生成数据的分布函数,Wasserstein 距离衡量了这两个分布函数的差异性。根据两个分布函数分别生成一堆数据 x1, x2, … , xn 和 y1, y2, … , yn,然后计算数据之间的距离。距离的算法是找到一种一一对应的配对方案 γ~∏(Pr, Pg),把 xi 移动到 yj,求总移动距离的最小值。Pr 和 Pg 都没有显式的表达式,只能是从里面不停地采样,所以不可能找到这样的 γ。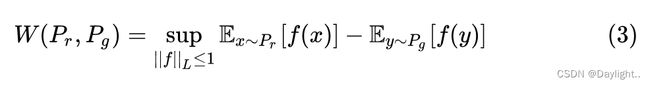 其中 f 即为判别器函数。只有当判别器函数满足 1-Lipschitz 约束时,(2) 才能转化为 (3)。除此之外,Lipschitz continuous 的函数的梯度上界被限制,因此函数更平滑,在神经网络的优化过程中,参数变化也会更稳定,不容易出现梯度爆炸,因此 Lipschitz continuity 有一个很好的性质。
其中 f 即为判别器函数。只有当判别器函数满足 1-Lipschitz 约束时,(2) 才能转化为 (3)。除此之外,Lipschitz continuous 的函数的梯度上界被限制,因此函数更平滑,在神经网络的优化过程中,参数变化也会更稳定,不容易出现梯度爆炸,因此 Lipschitz continuity 有一个很好的性质。
为了让判别器函数满足 1-Lipschitz continuity,W-GAN 和之后的 W-GAN GP 分别采用了 weight-clipping 和 gradient penalty 来约束判别器参数。这里的谱归一化,则是另一种让函数满足 1-Lipschitz continuity 的方式。
Spectral Normalization谱归一化
Spectral norm(谱范数)是参数矩阵W 的最大的奇异值。
在WGAN中,Lipschitz连续性对于确保最优鉴别器的有界性很重要。在WGAN的情况下,这使得潜在的鉴别器w损失函数是有效的。谱归一化有助于提高稳定性,避免模式崩溃等梯度消失问题。
Spectral Norm
在符号上,矩阵的谱范数通常表示为()。对于神经网络而言,矩阵表示网络某一层的权值矩阵。矩阵的谱范数是矩阵的最大奇异值,可以通过奇异值分解(SVD)得到。SVD是特征分解的推广,用于将一个矩阵分解为=Σ⊤,其中,是正交矩阵,Σ是其对角线上的奇异值矩阵。Σ不一定是方形的。
奇异值分解在谱归一化中的应用
要对权重矩阵进行谱归一化,需要将矩阵中的每个值除以其谱范数。
由于计算的SVD非常昂贵,所以SN-GAN论文的作者通过幂迭代分别逼近左右奇异向量̃和̃,使()≈̃⊤̃。
从随机初始化开始,̃和̃更新的根据:
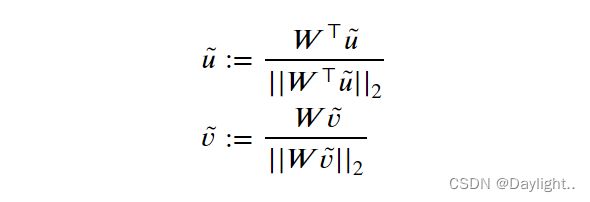 可以由torch.nn.utils.spectral_norm完成,只需要大致了解如何使用以及何时使用它就可以了。论文中,作者的描述:一轮迭代就足以“实现令人满意的性能”。
可以由torch.nn.utils.spectral_norm完成,只需要大致了解如何使用以及何时使用它就可以了。论文中,作者的描述:一轮迭代就足以“实现令人满意的性能”。
关于谱归一化的历史
这并不是谱范数第一次在深度学习模型中被提出。《Spectral Norm Regularization for Improving the Generalizability of Deep Learning》 (Yoshida et al . 2017年)提出了谱标准正规化,它们显示添加额外的损失,提高模型的普遍性方面到损失函数(L2正则化和梯度一样!)。这些额外损失惩罚权重的谱范数,可以认为这是与数据无关的正则化,因为关于的梯度不是小批处理的函数。
另一方面,谱归一化将权重矩阵的光谱范数设置为1——这是一个比添加损失项更难的约束,这是一种“软”正则化形式。正如作者在论文中所展示的,你可以把谱归一化看作是依赖于数据的正则化,因为关于的梯度依赖于小批量统计(论文的2.1节)。谱归一化基本上可以防止每一层在一个方向上变得敏感,并减轻爆炸梯度。
论文地址为:(https://arxiv.org/abs/1705.10941)
使用谱归一化的DCGAN
在DCGAN实现基础上,如何将谱归一化应用于DCGAN?
import torch
from torch import nn
from tqdm.auto import tqdm
from torchvision import transforms
from torchvision.datasets import MNIST
from torchvision.utils import make_grid
from torch.utils.data import DataLoader
import matplotlib.pyplot as plt
torch.manual_seed(0) # Set for our testing purposes, please do not change!
'''
Function for visualizing images: Given a tensor of images, number of images, and
size per image, plots and prints the images in an uniform grid.
'''
def show_tensor_images(image_tensor, num_images=25, size=(1, 28, 28)):
image_tensor = (image_tensor + 1) / 2
image_unflat = image_tensor.detach().cpu()
image_grid = make_grid(image_unflat[:num_images], nrow=5)
plt.imshow(image_grid.permute(1, 2, 0).squeeze())
plt.show()
DCGAN生成器
由于谱归一化只应用于鉴别器中的矩阵,因此生成器的实现与论文中相同。
class Generator(nn.Module):
'''
Generator Class
Values:
z_dim: the dimension of the noise vector, a scalar
im_chan: the number of channels of the output image, a scalar
MNIST is black-and-white, so that's our default
hidden_dim: the inner dimension, a scalar
'''
def __init__(self, z_dim=10, im_chan=1, hidden_dim=64):
super(Generator, self).__init__()
self.z_dim = z_dim
# Build the neural network
self.gen = nn.Sequential(
self.make_gen_block(z_dim, hidden_dim * 4),
self.make_gen_block(hidden_dim * 4, hidden_dim * 2, kernel_size=4, stride=1),
self.make_gen_block(hidden_dim * 2, hidden_dim),
self.make_gen_block(hidden_dim, im_chan, kernel_size=4, final_layer=True),
)
def make_gen_block(self, input_channels, output_channels, kernel_size=3, stride=2, final_layer=False):
'''
Function to return a sequence of operations corresponding to a generator block of the DCGAN,
corresponding to a transposed convolution, a batchnorm (except for in the last layer), and an activation
Parameters:
input_channels: how many channels the input feature representation has
output_channels: how many channels the output feature representation should have
kernel_size: the size of each convolutional filter, equivalent to (kernel_size, kernel_size)
stride: the stride of the convolution
final_layer: whether we're on the final layer (affects activation and batchnorm)
'''
# Build the neural block
if not final_layer:
return nn.Sequential(
nn.ConvTranspose2d(input_channels, output_channels, kernel_size, stride),
nn.BatchNorm2d(output_channels),
nn.ReLU(inplace=True),
)
else: # Final Layer
return nn.Sequential(
nn.ConvTranspose2d(input_channels, output_channels, kernel_size, stride),
nn.Tanh(),
)
def unsqueeze_noise(self, noise):
'''
Function for completing a forward pass of the Generator: Given a noise vector,
returns a copy of that noise with width and height = 1 and channels = z_dim.
Parameters:
noise: a noise tensor with dimensions (batch_size, z_dim)
'''
return noise.view(len(noise), self.z_dim, 1, 1)
def forward(self, noise):
'''
Function for completing a forward pass of the Generator: Given a noise vector,
returns a generated image.
Parameters:
noise: a noise tensor with dimensions (batch_size, z_dim)
'''
x = self.unsqueeze_noise(noise)
return self.gen(x)
def get_noise(n_samples, z_dim, device='cpu'):
'''
Function for creating a noise vector: Given the dimensions (n_samples, z_dim)
creates a tensor of that shape filled with random numbers from the normal distribution.
Parameters:
n_samples: the number of samples in the batch, a scalar
z_dim: the dimension of the noise vector, a scalar
device: the device type
'''
return torch.randn(n_samples, z_dim, device=device)
DCGAN判别器
对于判别器,可以对每个nn进行封装在Conv2d nn.utils.spectral_norm。在后端,除了之外,还引入了̃和̃的参数,以便W可以在运行时被计算为̃⊤̃。
Pytorch还提供了一个nn.utils.remove_spectral_norm函数,它将这3个单独的参数压缩成一个̃⊤̃。将此应用于卷积层,以提高运行时速度。
值得注意的是,谱范数并不能消除对模型对批范数的需要。谱范数影响每一层的权重,批范数影响每一层的激活。可以在discriminator架构中看到这两者。
class Discriminator(nn.Module):
'''
Discriminator Class
Values:
im_chan: the number of channels of the output image, a scalar
MNIST is black-and-white (1 channel), so that's our default.
hidden_dim: the inner dimension, a scalar
'''
def __init__(self, im_chan=1, hidden_dim=16):
super(Discriminator, self).__init__()
self.disc = nn.Sequential(
self.make_disc_block(im_chan, hidden_dim),
self.make_disc_block(hidden_dim, hidden_dim * 2),
self.make_disc_block(hidden_dim * 2, 1, final_layer=True),
)
def make_disc_block(self, input_channels, output_channels, kernel_size=4, stride=2, final_layer=False):
'''
Function to return a sequence of operations corresponding to a discriminator block of the DCGAN,
corresponding to a convolution, a batchnorm (except for in the last layer), and an activation
Parameters:
input_channels: how many channels the input feature representation has
output_channels: how many channels the output feature representation should have
kernel_size: the size of each convolutional filter, equivalent to (kernel_size, kernel_size)
stride: the stride of the convolution
final_layer: whether we're on the final layer (affects activation and batchnorm)
'''
# Build the neural block
if not final_layer:
return nn.Sequential(
nn.utils.spectral_norm(nn.Conv2d(input_channels, output_channels, kernel_size, stride)),
nn.BatchNorm2d(output_channels),
nn.LeakyReLU(0.2, inplace=True),
)
else: # Final Layer
return nn.Sequential(
nn.utils.spectral_norm(nn.Conv2d(input_channels, output_channels, kernel_size, stride)),
)
def forward(self, image):
'''
Function for completing a forward pass of the Discriminator: Given an image tensor,
returns a 1-dimension tensor representing fake/real.
Parameters:
image: a flattened image tensor with dimension (im_dim)
'''
disc_pred = self.disc(image)
return disc_pred.view(len(disc_pred), -1)
Training SN-DCGAN
将以上所有模块结合起来,训练一个谱归一化的DCGAN。用于初始化和优化的所有参数如下:
criterion = nn.BCEWithLogitsLoss()
n_epochs = 50
z_dim = 64
display_step = 500
batch_size = 128
# A learning rate of 0.0002 works well on DCGAN
lr = 0.0002
# These parameters control the optimizer's momentum, which you can read more about here:
# https://distill.pub/2017/momentum/ but you don’t need to worry about it for this course
beta_1 = 0.5
beta_2 = 0.999
device = 'cuda'
# We tranform our image values to be between -1 and 1 (the range of the tanh activation)
transform = transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((0.5,), (0.5,)),
])
dataloader = DataLoader(
MNIST(".", download=True, transform=transform),
batch_size=batch_size,
shuffle=True)
初始化生成器、判别器和优化器。
gen = Generator(z_dim).to(device)
gen_opt = torch.optim.Adam(gen.parameters(), lr=lr, betas=(beta_1, beta_2))
disc = Discriminator().to(device)
disc_opt = torch.optim.Adam(disc.parameters(), lr=lr, betas=(beta_1, beta_2))
# We initialize the weights to the normal distribution
# with mean 0 and standard deviation 0.02
def weights_init(m):
if isinstance(m, nn.Conv2d) or isinstance(m, nn.ConvTranspose2d):
torch.nn.init.normal_(m.weight, 0.0, 0.02)
if isinstance(m, nn.BatchNorm2d):
torch.nn.init.normal_(m.weight, 0.0, 0.02)
torch.nn.init.constant_(m.bias, 0)
gen = gen.apply(weights_init)
disc = disc.apply(weights_init)
Train
cur_step = 0
mean_generator_loss = 0
mean_discriminator_loss = 0
for epoch in range(n_epochs):
# Dataloader returns the batches
for real, _ in tqdm(dataloader):
cur_batch_size = len(real)
real = real.to(device)
## Update Discriminator ##
disc_opt.zero_grad()
fake_noise = get_noise(cur_batch_size, z_dim, device=device)
fake = gen(fake_noise)
disc_fake_pred = disc(fake.detach())
disc_fake_loss = criterion(disc_fake_pred, torch.zeros_like(disc_fake_pred))
disc_real_pred = disc(real)
disc_real_loss = criterion(disc_real_pred, torch.ones_like(disc_real_pred))
disc_loss = (disc_fake_loss + disc_real_loss) / 2
# Keep track of the average discriminator loss
mean_discriminator_loss += disc_loss.item() / display_step
# Update gradients
disc_loss.backward(retain_graph=True)
# Update optimizer
disc_opt.step()
## Update Generator ##
gen_opt.zero_grad()
fake_noise_2 = get_noise(cur_batch_size, z_dim, device=device)
fake_2 = gen(fake_noise_2)
disc_fake_pred = disc(fake_2)
gen_loss = criterion(disc_fake_pred, torch.ones_like(disc_fake_pred))
gen_loss.backward()
gen_opt.step()
# Keep track of the average generator loss
mean_generator_loss += gen_loss.item() / display_step
## Visualization code ##
if cur_step % display_step == 0 and cur_step > 0:
print(f"Step {cur_step}: Generator loss: {mean_generator_loss}, discriminator loss: {mean_discriminator_loss}")
show_tensor_images(fake)
show_tensor_images(real)
mean_generator_loss = 0
mean_discriminator_loss = 0
cur_step += 1
Step 500: Generator loss: 0.6946564222574235, discriminator loss: 0.6962353057861327


Step 50000: Generator loss: 0.6947942016124723, discriminator loss: 0.6942581459283822

