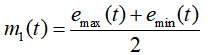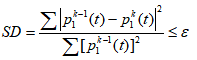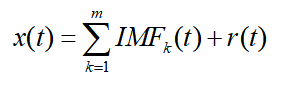二、信号分解 —＞经验模态分解（EMD）学习笔记
一、简述：
经验模态分解法(EMD)，基于瞬时频率、本征模态函数(Intrinsic Mode Function,IMF)的概念，能够将信号分解为若干个IMF分量，每个IMF表征信号的局部特征。依据的是数据自身的时间尺度特征来进行信号分解，无需预先设定任何基函数，因此具有自适应性。
二、基础概念：
1、解析信号
为什么要进行信号的解析？
采集的信号一般为时间尺度数据，要分析其特性一般把时间尺度变为频率尺度即信号的频率分析。如果把信号直接进行傅里叶变换后会使频域变为正频域和负频域（负频域现实世界是不存在的，只存在数学推导中），这就使得变换后的频域（正频域）缺失不完整，从而导致信号特性的缺失。
公式推导：
其中sgn(f)为符号函数
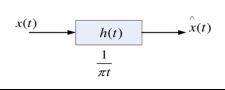
Hilbert变换可以看成是将原始信号通过一个滤波器，或者一个系统，这个系统的冲击响应为h(t)。
2、瞬时频率
为什么使用瞬时频率？
在传统频谱分析中，频率指是以傅里叶变换为基础的与时间无关的量：频率f或角频率w ，其实质是表示信号在一段时间内的总体特征，对于一般的平稳信号，传统的频域分析方法是有效的。但是对于实际中存在的非平稳信号，其频率是随时间变化的，此时傅里叶频率不再适合，为了表征信号的局部特性就需要引进瞬时频率的概念。
推导公式：
备注：不是任何解析信号都可以通过该定义得到有意义的瞬时频率，要得到有意义的瞬时频率，原始信号就必须满足严格的条件。
瞬时频率是时间t的单值函数，即每个时间t只有一个频率与之唯一对应，因此它只能表示单分量的信号，对于由多分量组合而成的信号，瞬时频率是没有实际的物理意义的，但在很多情况下是很难判断一个信号是单分量还是多分量，所以通常把“窄带信号” 作为信号选择的标准，使之符合瞬时频率的定义。
3、本特征模态
本征模式函数(Intrinsic Mode Function，IMF)的新概念，基于这类函数的局部特性，使函数的任何一点瞬时频率都有意义。
一个固有模式函数必须满足以下两个条件：
（1）整个数据长度中极值点和过零点的数目必须相等或至多相差一个；
（2）在研究对象的时域中，由三次样条拟合最大值和最小值点确定的上、下包络线的平均值是0。
通常情况下，实际信号都是复杂信号并不满足上述条件。因此，Huang进行了以下的假设：
（1）任何信号都是由若干本征模态函数组成的；
（2）各个本征模态函数即可是线性的，也可是非线性的，各本征模态函数的局部零点数和极值点数相同，同时上下包络关于时间轴局部对称；
（3）在任何时候，一个信号都可以包含若干本征模态函数，若各模态函数之间相互混叠，就组成了复合信号。
三、EMD的基本理论
1、找到原信号x(t)的所有极大值点，通过三次样条函数拟合出极大值包络线
；同理，找到原信号x(t)的所有极小值点，通过三次样条函数拟合出信号的极小值包络线
。注意：所有的极值点必须保证被上部和下部包络线包含。
2、计算上、下包络的平均值m1(t)：
3、将原信号序列减去m1(t)就得到一个去掉低频的新信号
：
一般不是一个平稳信号，不满足IMF定义的两个条件，重复上述过程，假定经过k次之后（k一般小于10）
满足IMF的定义，则原信号x(t)的一阶IMF分量为：
用原信号x(t)减去
，得到一个去掉高频成分的新信号
：
对重复得到的过程，得到第二个IMF分量
，如此反复进行，一直到第n阶IMF分量
或其余量
小于预设值；或当残余分量是单调函数或常量时，EMD分解过程停止。
最后， 原始信号经EMD分解，可以表示为：
在实际情况中，上下包络的均值无法为零，通常当满足下面的式子时，就认为包络的均值满足IMF的均值为零的条件：
当标准差SD的值在0.2和0.3之间，这时停止筛选是最合理的。
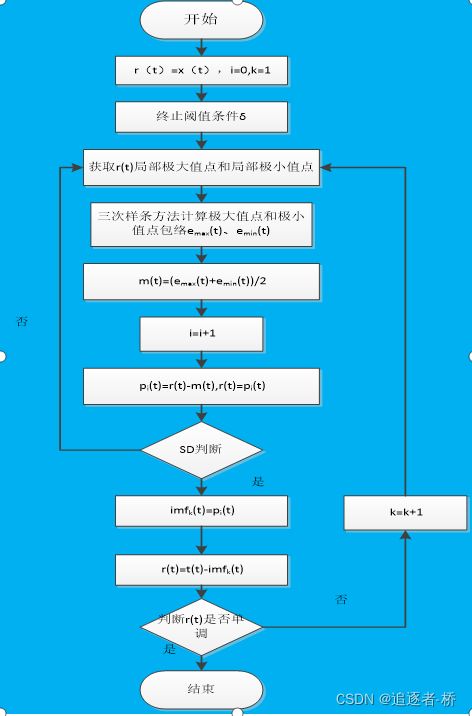
四、实现步骤
（1）初始化：r(t)=x(t)，i=0，k=1，终止阈值条件为SD<δ，一般情况下选择δ在0.2〜0.3之间；
（2）通过r(t)计算获取的局部极大值点和极小值点；使用三次样条曲线分别拟合极大值点和极小值点，得到信号的上、下包络线和，由上、下包络线计算其局部平均值，得到平均包络m(t);
（3）令i=i+1，从原始信号中减去均值包络，得到待鉴定分量
（4）计算终止迭代条件SD。由于在实际情况的限制，一般无法完全实现上包络线和下包络线的均值为零，通常情况下如果SD<δ ，则 
，进入下一步，否则令
,循环执行(2)-(4)；
（5）计算 
，判断r(t)是否单调，若其不单调，回到步骤（2），且执行k=k+1，直至r(t)为单调函数。最终信号分解为如下形式：
流程图：
注：EMD分解时，分解出来的模态信号是从高频信号到低频信号与VMD分解的模态信号是相反的。
五、分解结果
混叠模式介绍及程序图像输出判断
模态混叠就是指不能依据时间特征尺度（是通过频谱来反映出来的）有效地分离出不同的模态分量，使得原本不同的模态出现在一个模态中的现象。
即两个模态的中心频率非常接近，也就是说两个模态混叠了。
六、matlab代码
clc
clear all
close all
% 定义输入信号
Ts = (1/512);
Fs = 1/Ts;
t=0:Ts:1;
v1 = 0.5*cos(2*20*pi*t);
v2 = cos(2*30*pi*t);
input = v1+v2;
% x = awgn(input,1);
x=input;
%绘制出入信号时域图
figure
plot(t,x);
grid on
xlabel('t');ylabel('x');title('初始信号');
legend('0.5cos(40x*pi)+cos(60x*pi)');
%求取本证模态函数imf并绘制其时图像及频谱
imf = emd(x);
plot_hht(x,imf,1/Fs);
[M,N]=size(imf); %模态数及模态长度
%计算相关系数并绘制
for i = 1:1:N
cc(i)=min(min(corrcoef(imf{i},x)));
end
figure
plot(cc,'-g<','LineWidth',1.5,'MarkerEdgeColor','b','MarkerFaceColor','b','MarkerSize',5);
set(gca,'XGrid', 'on', 'YGrid', 'on');
legend('CC');
xlabel('IMF');
ylabel('相关系数');
%重构信号
cg_ev=imf{1}+imf{2};
figure;
plot(t,x);
hold on
plot(t,cg_ev,'r');
xlabel('t/s');ylabel('幅值');legend('原信号','重构信号');
%重构信号
cg_ev=imf{1}+imf{2}+imf{3}+imf{4}+imf{5}+imf{6};
figure;
plot(t,x)
hold on
plot(t,cg_ev,'r');
xlabel('t/s');ylabel('幅值');legend('原信号','重构信号');EMD代码：
https://download.csdn.net/download/ARM_qiao/85038211
https://download.csdn.net/download/ARM_qiao/85038211