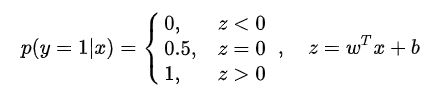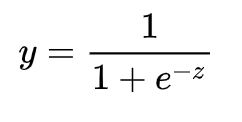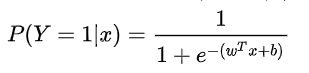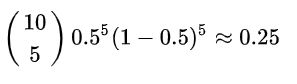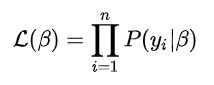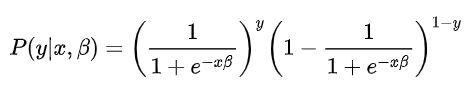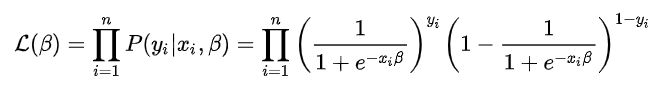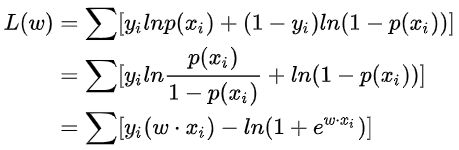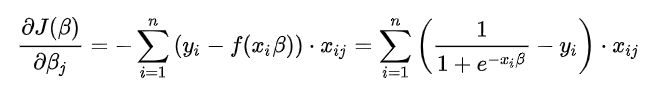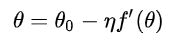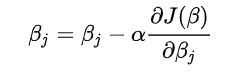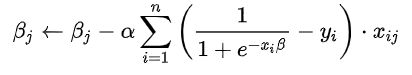推荐算法之逻辑回归
前言
从本文开始算是正式进入推荐算法的这一行列了。逻辑回归在推荐算法中有着举足轻重的地位,现在很多的算法几乎都多多少少有着逻辑回归的影子。相比较协同过滤,逻辑回归能够综合用户、物品和上下文等多种不同的特征,生成一个全面的结果。并且逻辑回归中的“感知机”也是作为神经网络中最基础的单一神经元,是深度学习的基础型结构。在传统的推荐系统中,逻辑回归衍生出来经典的模型和算法。例如常见的因子分解机FM,Facebook提出的GBDT+LR组合的模型,以及阿里巴巴曾经主流的推荐模型LS-PLM。今天就一起系统的来学习一下逻辑回归!!(激动)
一、逻辑回归
在介绍推荐算法中逻辑回归之前,我觉得很有必要先系统的学习一下什么是逻辑回归。逻辑回归细节很多,在这里写的不对的地方希望大家能够及时评论补充,感谢!Logistic Regression 虽然被称为回归,但其实际上是分类模型,并常用于二分类。逻辑回归因其简单、可并行化、可解释强深受工业界喜爱。我们以二分类为例,对于所给的数据集假设存在这样一个函数可以将这些数据完成划分。
决策边界可以看成y=f(wx+b)这样的一个函数,当y>0的时候就可以判定它的类别为1,这个过程就是感知机。因为给定的分界函数是连续的,而给定的数据往往是离散的,所以逻辑回归还要进行分类概率的判定,通过比较分类概率和输入向量X的关系来进行判定类别。最理想的讲就是单位阶跃函数。
当然不一定是p=0.5的时候进行分类,可以根据自己的设计来进行训练。这里一般都默认为0.5的时候为阶级跳跃。为了使概率函数可微,这里使用了大名鼎鼎的Sigmoid函数:
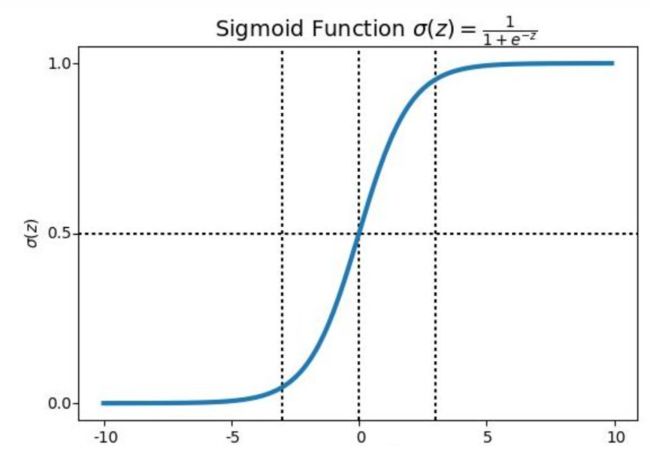
Sigmoid函数图像如下所示:
由上图可以看出,Sigmoid函数的值域 y 在(0,1)之间,这完美的解决了分类的问题,也就是0,1问题。逻辑回归的本质就是用线性回归带入simoid函数,得到的值位于0-1之间,代表着“可能性”,也就是用回归的思想解决了分类的问题。
一元线性回归方程可以用 y=wx+b 表示,而推广到多元函数,则可以写成矩阵的形式,也是向量形式,w表示各个特征相应的权重。因此,令P(Y=1)预测为正样本的概率 , 逻辑回归的数学形式为:
输入 x 的线性函数表示的模型,这就是逻辑回归模型。当 wx+b 的值越接近正无穷,P(Y=1) 概率值也就越接近 1。因此逻辑回归的思路是,先拟合决策边界(不局限于线性,还可以是多项式),再建立这个边界与分类的概率联系,从而得到了二分类情况下的概率。我们接下来需要做的就是求解参数矩阵W,在统计学中常常使用极大似然估计法来求解。
二、极大似然估计
我们首先帮助大家回忆一下极大似然估计,在概率论中极大似然估计是很重要的一个章节,不知道大家在大一学习的时候是怎么理解的,我在学习这里的时候,只是知道但凡看到这类的题目就直接两边使用对数函数(ln)然后求导,即可。仅仅是知道极大似然估计概率不太好求极大值,需要两边同时取对数,这样才方便求导。知道到了研究生才知道这背后的原理,接下来我就将自己的一些感悟体会写给大家,有所不足希望及时提出,谢谢啦。
极大似然估计:给定样本变量 x,参数未知,那么我们需要去推断其参数w,使得这件事发生概率 P得到最大化。
需要注意的是极大似然估计是不知道参数,要使得我们目前发生的事情概率最大,从而去求得适合的参数w,这一点要和求解概率分开。
举个简单的例子:
概率:我们已知硬币正反两面是公平的,因此参数 w 为0.5。 那么我们抛1次硬币,得到“数字”朝上的概率 P 就为50%,我们抛10次,出现5次“数字”朝上的概率 P就为:
在这件事情中,因为概率分布是满足伯努利的,by the way (放个洋p)在逻辑回归所有的情况下,我们都是假设这些数据液体同样满足伯努利分布。 我们需要假设不知道硬币正反变的概率p,即参数w,为了使得五次数字朝上的概率P最大,参数w是多少。
我们进行多次观察,当观测值为y1,y2,y3,....yn时他们同时发生的概率为:
这就变成了纯数学理论推导题了,即两边同时取对数,然后求导取得最优值β即可。
三、逻辑回归模型推导
好的,插播完最大似然估计的基础知识,接下来我们就进入到逻辑回归模型的推导阶段。请准备好公式的连番轰炸(还是很简单的,强烈建议大家手动推导一遍)。
在二分类伯努利分布上边,我们上边抛硬币的例子,只有P(Y=1)和P(Y=0)两种答案,所以我们可以将y的概率写成:
这个公式也是很容易理解的,即当y=0的时候P(y)=p(y=0)。y=1时,反之。那么我们将参数β引入,则公式改写为:
我们在第一节提到过为了能够更好的计算概率问题,我们引入了Sigmoid函数来进行计算,将Sigmoid函数函数代入到概率中得到:
根据极大似然估计原理,我们进行过多次数据观察后得到:
这样子看着有点复杂,为了简化公式,我们将Sigmoid函数函数重新换成概率P(y),然后利用最大似然估计基本原理进行求导,目的是获取一个β的值,使得L(β)最大。
四、逻辑回归的求解
前面讲了那么多,最后就是求解这一步了,求解逻辑回归的方法有很多(大佬们太厉害了),在这里最常用的就是牛顿法和梯度下降法。
牛顿法的基本思路是,在现有极小点估计值的附近对 f(x) 做二阶泰勒展开,进而找到极小点的下一个估计值。(取自一位大佬的文章,我就不多做解释了)
然后就是我们做机器学习必须需要掌握的一个算法了,即梯度下降。关于梯度下降的方式有很多,等着我会专门出一个系列介绍这些梯度下降的方式,包括优化器、正则化、损失函数之类的,还会带着大家手撕梯度下降(期待⭐),在这里就简单介绍一下。
根据梯度下降,为了得到梯度的方向,我们需要对参数求偏导,这里,就是对 L(β) 中的参数 β_i求偏导。这里注意,β是向量,同时也是各个特征的权重,因此,在这里我们需要对每个β_i求偏导, 也就是梯度:
然后根据梯度更新公式进行梯度更新:
得到:
带入到最终的模型参数更新公式:
其中α是学习率,至此为止我们就将逻辑回归的全部知识点讲解完毕了。在这里我肯定有很多的细节没有注意到,希望看到这篇文章的朋友们,可以给我及时指正,感谢!
五、逻辑回归在推荐系统中的应用
前面个讲了这么多,打了几千字,手都打酸了,终于到了本文的主题了,即推荐系统之逻辑回归。其实大家看到这里就已经知道的差不多了,接下来我就以文字的形式去表述一下逻辑回归算法在推荐系统中的应用。
基于逻辑回归的推荐过程如下所示:
(1)将用户年龄、性别、物品属性、物品描述、地点、时间等特征转换为数值型特征向量。
(2)确定逻辑回归模型的优化目标(以优化“点击率(CTR)”为例),利用已有样本对逻辑回归模型进行训练,确定逻辑回归模型内部参数。
(3)在模型服务阶段,将特征向量输入到逻辑回归模型,经过逻辑回归模型的推断,得到用户点击物品的概率。
(4)利用用户点击物品的概率对所有候选物品进行排序,进而得到推荐列表。
其中具体一点的步骤就是将获取到的特征向量x=(x1,x2,x3,...,x_n)作为模型的输入,然后获取为各个特征赋予的权重(w1,w2,w3,....w_n),将xw进行加权求和。
逻辑回归的优势在于:
- 可解释性强。 sigmoid函数很好的解释了二分类的问题。同时,在训练过程中的不同特征的权重,也代表了特征的重要性。
- 形式简单,训练速度快。 用SGD来优化逻辑回归,其训练开销小,模型简单,易于实现。
缺点:
- 表达能力有限。 不能进行特征交叉,特征筛选等工作,有信息损失。
- 只在处理二分类问题上优势明显。
逻辑回归在机器学习的发展中,占据了非常重要的地位。以逻辑回归为基础发展出来的模型非常的多,接下来我也会对一些经典的模型进行一一详解。到这里本篇文章就结束了,感谢大家的阅读!
参考:《深度学习推荐系统》
https://zhuanlan.zhihu.com/p/149788542
https://zhuanlan.zhihu.com/p/74874291