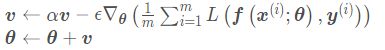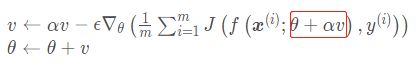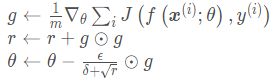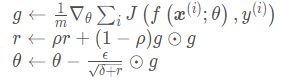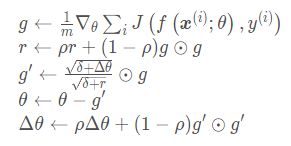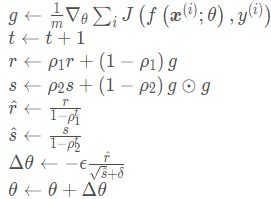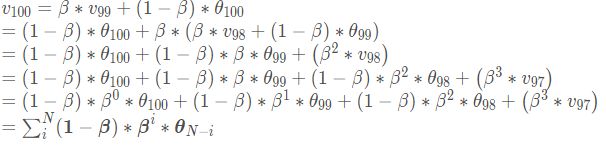深度学习之优化器（优化算法）

前言

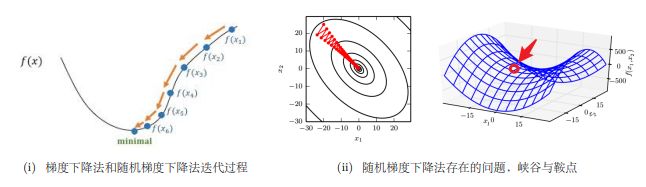
前面已经讲过几中梯度下降算法了，并且给了一个收尾引出这一章节，想看的小伙伴可以去看看这一篇文章：机器学习之梯度下降算法。前面讲过对SGD来说，最要命的是SGD可能会遇到“峡谷”和“鞍点”两种困境峡谷类似⼀个带有坡度的狭长小道，左右两侧是 “峭壁”；在峡谷中，准确的梯度方向应该沿着坡的方向向下，但粗糙的梯度估计使其稍有偏离就撞向两侧的峭壁，然后在两个峭壁间来回震荡。鞍点的形状类似⼀个马鞍，⼀个方向两头翘，⼀个方向两头垂，而中间区域近似平地；⼀旦优化的过程中不慎落入鞍点，优化很可能就会停滞下来(坡度不明显，很可能走错方向，如果梯度为0的区域，SGD无法准确察觉出梯度的微小变化，结果就停下来)。为了形象，还找了个图：

 

所以接下来的一些算法，就是针对于SGD的这两个要命问题进行的一系列改进了，首先先把握住改进的两个大方向： 惯性保持和环境感知

惯性保持： 加入动量， 代表：Momentum, Nesterov Accerlerated Gradient
环境感知： 根据不同参数的一些经验性判断， 自适应的确定每个参数的学习速率，这是一种自适应学习率的优化算法。代表：AdaGrad, AdaDelta, RMSProp
还有把上面两个方向结合的： Adam, AdaMax, Nadam

一、Momentum

动量顾名思义就是给这个梯度下降加了一个动力，这样子是为了更好的解决随机梯度下降中的“峡谷”和“鞍点”问题，并且能够使得在相同方向时下降速度更快。用《百面机器学习》上的一个比喻：如果把原始的 SGD 想象成⼀个纸团在重力作用向下滚动，由于质量小受到山壁弹力的干扰大，导致来回震荡。或者在鞍点处因为质量小速度很快减为 0，导致无法离开这块平地。动量方法相当于把纸团换成了铁球。不容易受到外力的干扰，轨迹更加稳定，同时因为在鞍点处因为惯性的作用，更有可能离开平地。

接下来看一下为什么会解决上述问题：动量算法积累了之前梯度指数级衰减的移动平均，并且继续沿该方向移动。用大白话结合下面公式来讲就是将之前梯度下降的动量给保留下来了，并在第t次梯度下降的时候，将其和所求的的下降动量进行相加，使得之前的下降动量影响了现在的下降动量。

从形式上看，动量算法引入了变量v 充当速度角色，以及相关的超参数α ，决定了之前的梯度贡献衰减的有多快。在这里我们一般设超参数α=0.9.原始的SGD每次更新的步长只是梯度乘以学习率。现在，步长还取决于历史梯度序列的大小和排列。 当许多连续的梯度指向相同的方向时，步长就会不断的增大，这就解决了在鞍点处速度减少为0的情况。

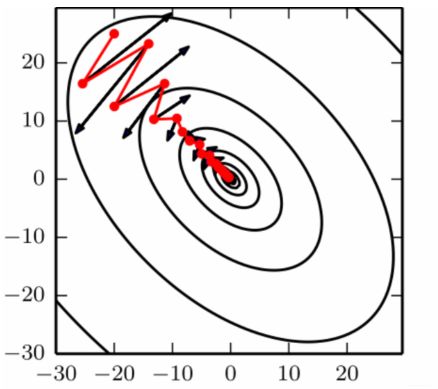
所以当前迭代点的下降方向不仅仅取决于当前的梯度，还受到前面所有迭代点的影响。动量方法以一种廉价的方式模拟了二阶梯度(牛顿法)。撤了这么半天理论，拿个图来看看效果：

 

optimizer = tf.train.MomentumOptimizer(learning_rate=learning_rate,
                                            momentum=0.9)

使用动量的SGD算法流程：

 二、NAG算法

Nesterov Accelerated Gradient 提出了⼀个针对动量算法的改进措施。动量算法是把历史的梯度和当前的梯度进进行合并，来计算下降的⽅向。而Nesterov 提出，让迭代点先按照历史梯度走⼀步，然后再合并。这种情况相当于小球从山上滚下来时是在盲目地沿着坡滚，如果它能具备一些先知，例如快要上坡时，就知道需要减速了的话，适应性会更好。更新规则如下，改变主要在于梯度的计算上：

 可以看到，在进行求梯度的时候，就将历史梯度和参数θ一起求导，这样就具有了先知的能力。Nesterov动量和标准动量之间的区别在于梯度计算上。 NAG把梯度计算放在了对参数施加当前速度之后， 往前走了一步J(f(x(i);θ+αv) 。这个提前量的设计让算法有了对前方环境的预判能力，可以理解为Nesterov动量往标准动量方法中添加了一个校正因子。

optimizer = tf.train.MomentumOptimizer(learning_rate=learning_rate,
                                           momentum=0.9, use_nesterov=True)

 完整的Nesterov动量算法流程：

 三、AdaGrad算法（加入环境感知）

目前为止可以实现在更新梯度时顺应 loss function 的梯度来调整速度，并且对 SGD 进行加速。但是接下来加入环境感知希望还可以实现根据参数的重要性而对不同的参数进行不同程度的更新。SGD对环境的感知是指在参数空间中，根据不同参数的一些经验性判断，自适应的确定参数的学习速率，不同参数的更新步幅是不同的。Adaptive Gradient算法的思想是独立地适应模型的每个参数(自动改变学习速率)，可以对低频的参数做较大的更新，对高频的做较小的更新，也因此，对于稀疏的数据它的表现很好，很好地提高了 SGD 的鲁棒性，对于进场更新的参数，能够更好的避免单个噪声的影响，而对于边缘参数，又可以更好地捕捉到它们的变化。具体来说，每个参数的学习率会缩放各参数反比于其历史梯度平方值总和的平方根，更新公式：

 r为累积平方梯度，其中 是个对角矩阵， (i,i) 元素就是 t 时刻参数 θ_i 的梯度平方和。但是同样存在很严重的问题，历史梯度在分母上的累积会越来越大， 所以学习率会越来越小， 使得中后期网络的学习能力越来越弱。

具体的算法流程：

 四、RMSProp和AdaDelta

RMSProp 是 Geoff Hinton 提出的一种自适应学习率方法。RMSprop 和 Adadelta都是为了解决Adagrad 学习率过度衰减问题的。AdaGrad 根据平方梯度的整个历史来收缩学习率，可能使得学习率在达到局部最小值之前就变得太小而难以继续训练。RMSProp 算法修改 AdaGrad 以在非凸设定下效果更好，改变梯度积累为指数加权平均。通俗的解释一下指数加权平均就是将指数的平方和使用一个衰减系数来控制历史信息量，进而改变训练提前停止的情况。

RMSProp 使用指数衰减平均以丢弃遥远过去的历史，使其能够在找到凸碗状结构后快速收敛，它就像一个初始化于该碗状结构的 AdaGrad 算法实例。RMSProp类似于Momentum中的做法，与Momentum的效果一样，某一维度的导数比较大，则指数加权平均就大，某一维度的导数比较小，则其指数加权平均就小，这样就保证了各维度导数都在一个量级，进而减少了摆动。允许使用一个更大的学习率。

optimizer = tf.train.RMSPropOptimizer(learning_rate=learning_rate,
                                      momentum=0.9, decay=0.9, epsilon=1e-10)

 RMSProp的算法流程如下：

 AdaDelta算法没有学习率这一超参数。 AdaDelta算法维护一个额外的变量Δ θ \Delta \thetaΔθ， 来计算自变量变化量按元素平方的指数加权移动平均：

 五、Adam算法(Adaptive Moment Estimation)

如果说前面所有的优化算法都是在一步一步的进行改进，那么Adam就是集大成者。它集合了全面所有优化算法的思想，将惯性保持和环境感知集于一身。Adam记录梯度的一阶矩，即过往梯度与当前梯度的平均，体现了保持惯性—历史梯度的指数衰减平均。Adam记录梯度的二阶矩， 即过往梯度平方与当前梯度平方的平均，RMSProp的方式，体现了环境感知的能力，为不用参数产生自适应的学习速率 — 历史梯度平方的指数衰减平均。

一阶矩和二阶矩类似于滑动窗口内求平均的思想进行融合，即当前梯度和近一段时间内的梯度平均值，时间久远的梯度为当前平均值贡献呈指数衰减。参数更新方式如下：

optimizer = tf.train.AdamOptimizer(learning_rate=learning_rate)

Adam算法流程如下

除了集动量保持和环境感知于一体之外，还添加了偏差修订，首先 s 和r 初始化为0， 且和推荐的初始值都很接近1(0.9和0.999)，可以从算法中看到求出s 和 r之后并没有直接进行梯度下降，而是重新进行了计算。如果此刻不进行偏差修订，则当刚刚进行梯度下降的时候，，所欲我们需要进行偏差修订,使得过去各时间步小批量随机梯度权值之和为1。Adam通常被认为对超参数的选择相当鲁棒。

六、指数滑动平均

上面很多优化算法都用到了一个思想就是指数滑动平均，在这里单独讲一下加深印象。指数加权平均在时间序列中经常用于求取平均值的一个方法，它的思想是这样，我们要求取当前时刻的平均值，距离当前时刻越近的那些参数值，它的参考性越大，所占的权重就越大，这个权重是随时间间隔的增大呈指数下降，所以叫做指数滑动平均，公式如下：

 当然了，看到这里还是很不理解这个公式是怎么就使得距离时间越远的参数值就权重越小，却呈现指数型下降的。首先先看有一个例子。

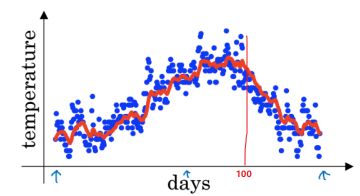
 看上面这个温度图像，横轴是第几天，然后纵轴是温度， 假设我想求第100天温度的一个平均值，那么根据上面的公式：

 因为β是小于1 的，所以距离当前时刻越远的那些θ 值，它的权重是越来越小的，而且是呈指数下降，因为这里是。我们可以发现，beta越小，就会发现它关注前面一段时刻的距离就越短，比如这个0.8， 会发现往前关注20天基本上后面的权重都是0了，意思就是说这时候是平均的过去20天的温度， 而0.98这个，会发现，关注过去的天数会非常长，也就是说这时候平均的过去50天的温度。所以β在这里控制着记忆周期的长短，或者平均过去多少天的数据。

 

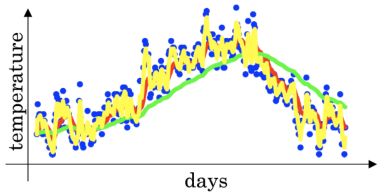
看上图，是不同beta下得到的一个温度变化曲线

• 绿色的那条，是beta=0.98， 也就是过去50天温度的平均值
• 红色的那条，是beta=0.9， 也就是过去10天温度的平均值
• 黄色的那条，beta=0.5， 也就是过去2天的温度的平均

可以发现，如果这个β 很高， 比如0.98， 最终得到的温度变化曲线就会平缓一些，因为多平均了几天的温度， 缺点就是曲线进一步右移， 因为现在平均的温度值更多， 要平均更多的值， 指数加权平均公式，在温度变化时，适应的更缓慢一些，所以会出现一些延迟，因为如果β=0.98，这就相当于给前一天加了太多的权重，只有0.02当日温度的权重,所以温度变化时，温度上下起伏，当β 变大时，指数加权平均值适应的更缓慢一些, 换了0.5之后，由于只平均两天的温度值，平均的数据太少，曲线会有很大的噪声，更有可能出现异常值，但这个曲线能够快速适应温度的变化。 所以这个β 过大过小，都会带来问题。 一般取0.9.

 Momentum梯度下降，基本的想法就是计算梯度的指数加权平均数，并利用该梯度更新权重，这就是动量的含义了，考虑了之前的梯度保持着一种惯性。而像RMSProp里面的历史梯度平方的指数加权衰减，AdaDelta里面的，Adam里面的指数加权等，其实都是这个意思，考虑前面的梯度或者梯度的平方，求一个平均值来更新当前参数。

最后说一句如何取选择优化算法呢，在这其实并没有一个固定的答案，毕竟深度学习的确有点玄学（狗头保命。

对于稀疏数据，尽量使用学习率可自适应的优化方法，不用手动调节，而且最好采用默认值。
SGD通常训练时间更长，但是在好的初始化和学习率调度方案的情况下（很多论文都用SGD），结果更可靠。并且适用于在线的实时更新，推荐里面可是常用
如果在意更快的收敛，并且需要训练较深较复杂的网络时，推荐使用学习率自适应的优化方法。
Adadelta，RMSprop，Adam是比较相近的算法，在相似的情况下表现差不多 。Adam 就是在 RMSprop 的基础上加了 bias-correction 和 momentum，随着梯度变得稀疏，Adam 比 RMSprop 效果会好。整体来讲，Adam 是最好的选择。

参考：重温深度学习优化算法