机器学习——kMeans聚类
相关概念
无监督学习
无监督学习是从无标注的数据中学习数据的统计规律或者说内在结构的机器学习,主要包括聚类、降维、概率估计。无监督学习可以用于数据分析或者监督学习的前处理。
聚类
聚类(clustering)是针对给定的样本,一句他们特征的相似或距离,将其归并到若干个簇的数据分析问题。直观上,相似的样本聚集在相同的簇,不相似的样本分散在不同的簇。因此,样本之间的相似度或距离起着重要作用。
相似度和距离的衡量:
样本矩阵 X X X的表示:
X = [ x i j ] m × n = [ x 11 x 12 ⋯ x 1 n x 21 x 22 ⋯ x 2 n ⋮ ⋮ ⋮ x m 1 x m 2 ⋯ x m n ] X=\left[x_{ij}\right]_{m\times n}=\begin{bmatrix}x_{11}&x_{12}&\cdots&x_{1n}\\x_{21}&x_{22}&\cdots&x_{2n}\\\vdots&\vdots& &\vdots\\x_{m1}&x_{m2}&\cdots&x_{mn}\end{bmatrix} X=[xij]m×n=⎣⎢⎢⎢⎡x11x21⋮xm1x12x22⋮xm2⋯⋯⋯x1nx2n⋮xmn⎦⎥⎥⎥⎤
1:闵可夫斯基斯基距离: d i j = ( ∑ k = 1 m ∣ x k i − x k j ∣ p ) 1 p d_{ij}=\left(\sum\limits_{k=1}^m\left|x_{ki}-x_{kj}\right|^p\right)^{\frac{1}{p}} dij=(k=1∑m∣xki−xkj∣p)p1。在聚类中,可以将样本集合看作是向量空间重点的集合,以该空间的距离表示样本之间的相似度。闵可夫斯基距离越大,表示相似度越小,否则相似度越高。
2:马哈拉诺比斯距离: d i j = [ ( x i − x j ) T S − 1 ( x i − x j ) ] 1 2 d_{ij}=\left[(x_i-x_j)^TS^{-1}(x_i-x_j)\right]^\frac{1}{2} dij=[(xi−xj)TS−1(xi−xj)]21,其中 S S S表示协方差矩阵协方差, x i = ( x 1 i , x 2 i , ⋯ , x m i ) T , x j = ( x 1 j , x 2 j , ⋯ , x m j ) T x_i=\left(x_{1i},x_{2i},\cdots,x_{mi}\right)^T,x_j=\left(x_{1j},x_{2j},\cdots,x_{mj}\right)^T xi=(x1i,x2i,⋯,xmi)T,xj=(x1j,x2j,⋯,xmj)T,简称马氏距离,也是常用的相似度,考虑各个特征之间的相关特性并与各个分量的尺度无关。马氏距离越大,则相似度越小,否则越大。
3:相关系数:样本之间的相似度可以用相关系数(correlation coefficient)来表示,相关系数的绝对值越接近于1,表示样本越相似;越接近于0,表示样本越不相似。样本 x i x_i xi与样本 x j x_j xj的相关系数定义为:
r i j = ∑ k = 1 m ( x k i − x ˉ i ) ( x k j − x ˉ j ) [ ∑ k = 1 m ( x k i − x ˉ i ) 2 ( x k j − x ˉ j ) 2 ] 1 2 r_{ij}=\frac{\sum\limits_{k=1}^m(x_{ki}-\bar x_i)(x_{kj}-\bar x_j)}{\left[\sum\limits_{k=1}^m(x_{ki}-\bar x_i)^2(x_{kj}-\bar x_j)^2\right]^\frac{1}{2}} rij=[k=1∑m(xki−xˉi)2(xkj−xˉj)2]21k=1∑m(xki−xˉi)(xkj−xˉj)
其中: x ˉ i = 1 m ∑ k = 1 m x k i , x ˉ j = 1 m ∑ k = 1 m x k j \bar x_i=\frac{1}{m}\sum\limits_{k=1}^m x_{ki},\ \bar x_j=\frac{1}{m}\sum\limits_{k=1}^m x_{kj} xˉi=m1k=1∑mxki, xˉj=m1k=1∑mxkj
4:夹角余弦:
样本之间的相似度也可以用夹角余弦(cosine)来表示。夹角余弦越接近于1,表示样本越相似;越接近于0,表示样本越不相似。样本 x i x_i xi与样本 x j x_j xj的夹角余弦定义为:
s i j = ∑ k = 1 m x k i x k j [ ∑ k = 1 m x k i 2 ∑ k = 1 m x k j 2 ] 1 2 s_{ij}=\frac{\sum\limits_{k=1}^m x_{ki}x_{kj}}{\left[\sum\limits_{k=1}^mx_{ki}^2\sum\limits_{k=1}^mx_{kj}^2\right]^\frac{1}{2}} sij=[k=1∑mxki2k=1∑mxkj2]21k=1∑mxkixkj
k均值聚类
k均值聚类是基于样本集合划分的聚类算法,将样本集合 D D D划分为k个子集,构成k个簇 { C l ∣ l = 1 , 2 , ⋯ , k } \left\{C_l|l=1,2,\cdots,k\right\} {Cl∣l=1,2,⋯,k},将n个样本分到k个簇中,每个样本到其所属簇的中心的距离最小,且每个样本只属于一个簇。
用 d x , y d_{x,y} dx,y表示两个向量之间的距离,则k均值算法的损失函数为:
W ( C ) = ∑ l = 1 k ∑ x ∈ C l d x , x ˉ l W(C)=\sum\limits_{l=1}^k\sum\limits_{x \in C_l}d_{x,\bar x_l} W(C)=l=1∑kx∈Cl∑dx,xˉl
其中, x ˉ l = 1 ∣ C l ∣ ∑ x ∈ C l \bar x_l=\frac{1}{|C_l|}\sum x\in C_l xˉl=∣Cl∣1∑x∈Cl。
得到k均值算法的目标优化函数:
C ∗ = a r g min C W ( C ) C^*=arg\ \min_CW(C) C∗=arg CminW(C)
相似的样本被聚到同一个簇时,损失值最小,但是,把n个样本分到k类是一个组合优化问题,分的方式是指数级别的,所以采用了贪心策略,通过迭代的方式来近似求解。
代码
相关数据:
/**
* Manhattan distance.
*/
public static final int MANHATTAN = 0;
/**
* Euclidean distance.
*/
public static final int EUCLIDEAN = 1;
/**
* The distance measure.
*/
public int distanceMeasure = EUCLIDEAN;
/**
* A random instance.
*/
public static final Random random = new Random();
/**
* The number of clusters.
*/
int numClusters = 2;
/**
* The whole data set.
*/
Instances dataset;
/**
* The clusters.
*/
int[][] clusters;
在构造函数中,读取数据获取样本:
(采用的是鸢尾花的数据,但没有用最后一列的标签)
public KMeans(String paraFilename) {
dataset = null;
try {
FileReader fileReader = new FileReader(paraFilename);
dataset = new Instances(fileReader);
fileReader.close();
} catch (Exception ee) {
System.out.println("Cannot read the file: " + paraFilename + "\r\n" + ee);
System.exit(0);
} // Of try
}// Of the first constructor.
一个setter函数,用来设置簇的个数:
/**
********************
* A setter
*********************
*/
public void setNumClusters(int paraNumClusters) {
numClusters = paraNumClusters;
}// Of the setter
获取随机索引,打乱数据顺序,和之前的KNN的一样,但这里只有在初始化簇的质心时用到那么一次,所以我认为在那里随机选numClusters个样本也是一样的:
/**
********************
* Get a random indices for data randomization.
*
* @param paraLength The length of the sequence.
* @return An array of indices.
*********************
*/
public static int[] getRandomIndices(int paraLength) {
int[] resultIndices = new int[paraLength];
// Step 1. Initialize.
for (int i = 0; i < paraLength; i++) {
resultIndices[i] = i;
} // Of for i
// Step 2. Randomly swap.
int tempFirst, tempSecond, tempValue;
for (int i = 0; i < paraLength; i++) {
// Generate two random indices.
tempFirst = random.nextInt(paraLength);
tempSecond = random.nextInt(paraLength);
// Swap
tempValue = resultIndices[tempFirst];
resultIndices[tempFirst] = resultIndices[tempSecond];
resultIndices[tempSecond] = tempValue;
} // Of for i
return resultIndices;
}// Of getRandomIndices
计算样本到质心的距离,由于质心有可能不是实际存在的样本点,所以第二个参数是一个数组:
/**
********************
* The distance between two instances.
*
* @param paraI The index of the first instance.
* @param paraArray The array representing a point in the space.
* @return The distance.
*********************
*/
public double distance(int paraI, double[] paraArray) {
int resultDistance = 0;
double tempDifference;
switch (distanceMeasure) {
case MANHATTAN:
for (int i = 0; i < dataset.numAttributes() - 1; i++) {
tempDifference = dataset.instance(paraI).value(i) - paraArray[i];
if (tempDifference < 0) {
resultDistance -= tempDifference;
} else {
resultDistance += tempDifference;
} // Of if
} // Of for i
break;
case EUCLIDEAN:
for (int i = 0; i < dataset.numAttributes() - 1; i++) {
tempDifference = dataset.instance(paraI).value(i) - paraArray[i];
resultDistance += tempDifference * tempDifference;
} // Of for i
break;
default:
System.out.println("Unsupported distance measure: " + distanceMeasure);
}// Of switch
return resultDistance;
}// Of distance
代码的核心:
/**
********************
* Clustering.
*********************
*/
public void clustering() {
int[] tempOldClusterArray = new int[dataset.numInstances()];
tempOldClusterArray[0] = -1;
int[] tempClusterArray = new int[dataset.numInstances()];
Arrays.fill(tempClusterArray, 0);
double[][] tempCenters = new double[numClusters][dataset.numAttributes() - 1];
// Step 1. Initialize centers.
int[] tempRandomOrders = getRandomIndices(dataset.numInstances());
for (int i = 0; i < numClusters; i++) {
for (int j = 0; j < tempCenters[0].length; j++) {
tempCenters[i][j] = dataset.instance(tempRandomOrders[i]).value(j);
} // Of for j
} // Of for i
int[] tempClusterLengths = null;
while (!Arrays.equals(tempOldClusterArray, tempClusterArray)) {
System.out.println("New loop...");
tempOldClusterArray = tempClusterArray;
tempClusterArray = new int[dataset.numInstances()];
// Step 2.1 Minimization.Assign cluster to each instance.
int tempNearestCenter;
double tempNearestDistance;
double tempDistance;
for (int i = 0; i < dataset.numInstances(); i++) {
tempNearestCenter = -1;
tempNearestDistance = Double.MAX_VALUE;
for (int j = 0; j < numClusters; j++) {
tempDistance = distance(i, tempCenters[j]);
if (tempDistance < tempNearestDistance) {
tempNearestDistance = tempDistance;
tempNearestCenter = j;
} // Of if
} // Of for j
tempClusterArray[i] = tempNearestCenter;
} // Of for i
// Step 2.2 Mean. Find new centers.
tempClusterLengths = new int[numClusters];
Arrays.fill(tempClusterLengths, 0);
double[][] tempNewCenters = new double[numClusters][dataset.numAttributes() - 1];
for (int i = 0; i < dataset.numInstances(); i++) {
for (int j = 0; j < tempNewCenters[0].length; j++) {
tempNewCenters[tempClusterArray[i]][j] += dataset.instance(i).value(j);
} // Of for j
tempClusterLengths[tempClusterArray[i]]++;
} // Of for i
// Step 2.3 Now average.
for (int i = 0; i < tempNewCenters.length; i++) {
for (int j = 0; j < tempNewCenters[0].length; j++) {
tempNewCenters[i][j] /= tempClusterLengths[i];
} // Of for j
} // Of for i
System.out.println("Now the new centers are: " + Arrays.deepToString(tempNewCenters));
tempCenters = tempNewCenters;
} // Of while
// Step 3. Form clusters.
clusters = new int[numClusters][];
int[] tempCounters = new int[numClusters];
for (int i = 0; i < numClusters; i++) {
clusters[i] = new int[tempClusterLengths[i]];
} // Of for i
for (int i = 0; i < tempClusterArray.length; i++) {
clusters[tempClusterArray[i]][tempCounters[tempClusterArray[i]]] = i;
tempCounters[tempClusterArray[i]]++;
} // Of for i
System.out.println("The clusters are: " + Arrays.deepToString(clusters));
}// Of clustering
最开始时,需要随机选择numClusters个样本,作为质心,这里的随机就通过getRandomIndices实现:
int[] tempRandomOrders = getRandomIndices(dataset.numInstances());
for (int i = 0; i < numClusters; i++) {
for (int j = 0; j < tempCenters[0].length; j++) {
tempCenters[i][j] = dataset.instance(tempRandomOrders[i]).value(j);
} // Of for j
} // Of for i
为了能更好感受迭代过程,我想通过图形对比来实现,由于样本的特征一共有四维,但主要是针对花瓣的长和宽、花萼的长和宽,所以我用了两个图来体现:
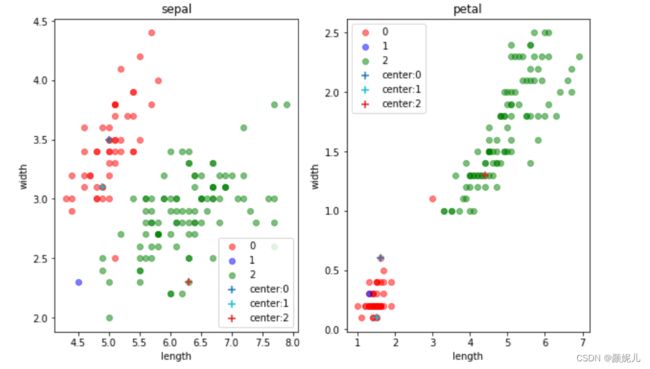
(是不是编号为1的簇看起来太惨了,我觉得有两个原因:一是毕竟是随机的,可能取的点偏了点;二是:因为我用了两个二维来表示四维,可能在真正的四维下看起来就不是这样了,先不要慌,我们是体验它的过程,再看看~)
while循环就是不断迭代,去找近似最优解,当发现质心不再改变(各个簇的样本不再改变),就说明分完了。
这个for循环是将每个样本分给离它最近的簇(样本到质心距离最短)
for (int i = 0; i < dataset.numInstances(); i++) {
tempNearestCenter = -1;
tempNearestDistance = Double.MAX_VALUE;
for (int j = 0; j < numClusters; j++) {
tempDistance = distance(i, tempCenters[j]);
if (tempDistance < tempNearestDistance) {
tempNearestDistance = tempDistance;
tempNearestCenter = j;
} // Of if
} // Of for j
tempClusterArray[i] = tempNearestCenter;
} // Of for i
上面分完样本之后,簇的子集就有可能会发生变化,所以要更新质心:
tempClusterLengths = new int[numClusters];
Arrays.fill(tempClusterLengths, 0);
double[][] tempNewCenters = new double[numClusters][dataset.numAttributes() - 1];
for (int i = 0; i < dataset.numInstances(); i++) {
for (int j = 0; j < tempNewCenters[0].length; j++) {
tempNewCenters[tempClusterArray[i]][j] += dataset.instance(i).value(j);
} // Of for j
tempClusterLengths[tempClusterArray[i]]++;
} // Of for i
// Step 2.3 Now average.
for (int i = 0; i < tempNewCenters.length; i++) {
for (int j = 0; j < tempNewCenters[0].length; j++) {
tempNewCenters[i][j] /= tempClusterLengths[i];
} // Of for j
} // Of for i
更新了质心,就又要去更新一下子集,直到各个簇的子集都不变了,就跳出while。
现在,就来感受一下更新的过程:
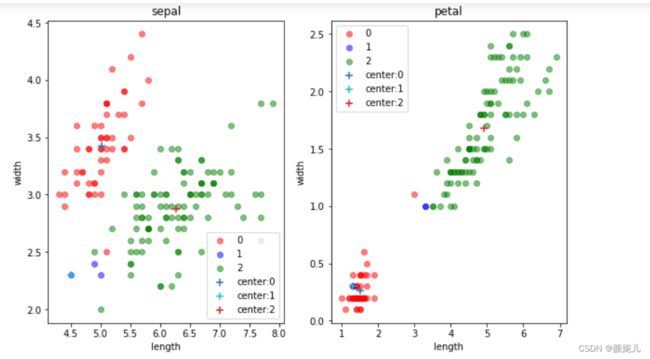
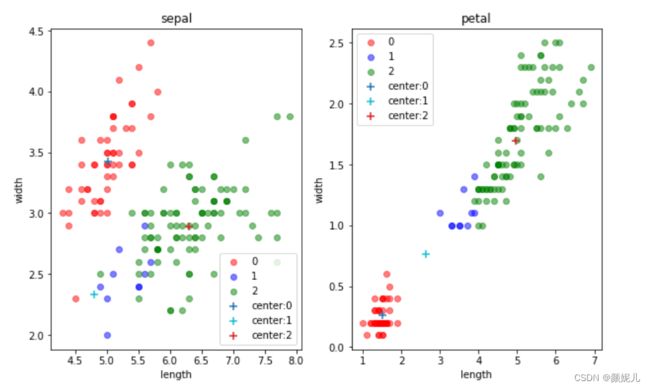
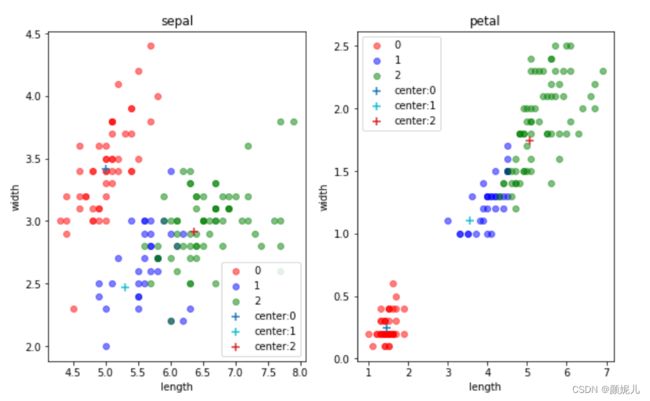
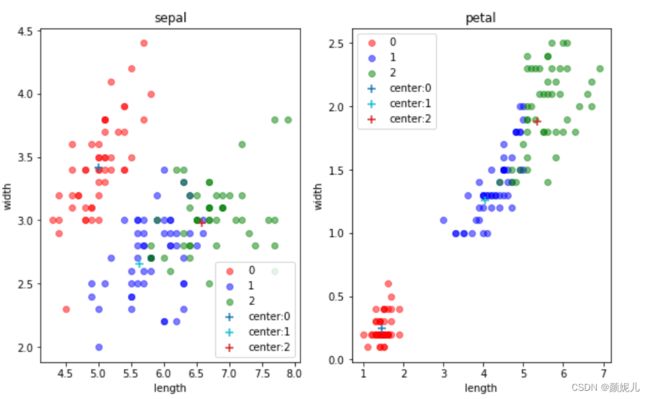
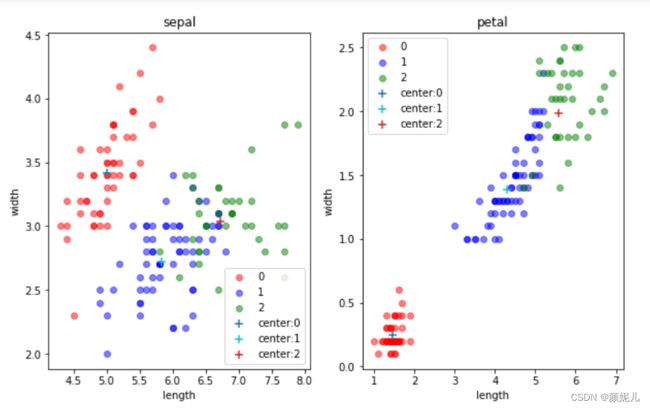

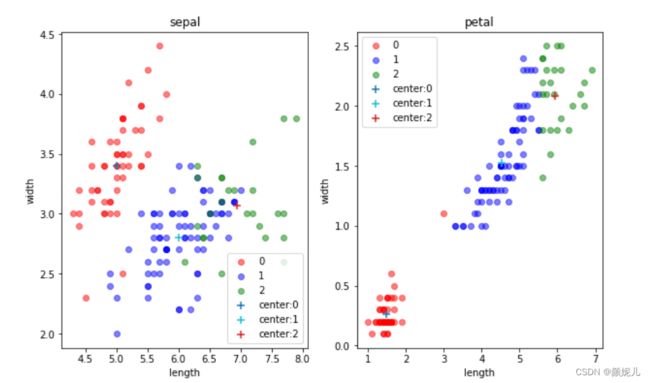
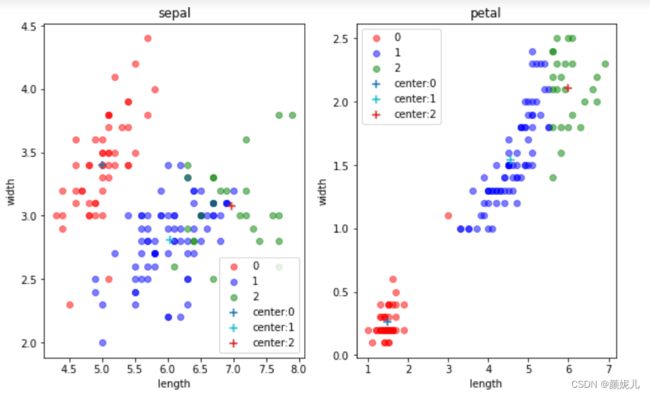
上面就是最后分簇的结果了,现在来看看用数据本身的标签画出来的图是怎么样的:
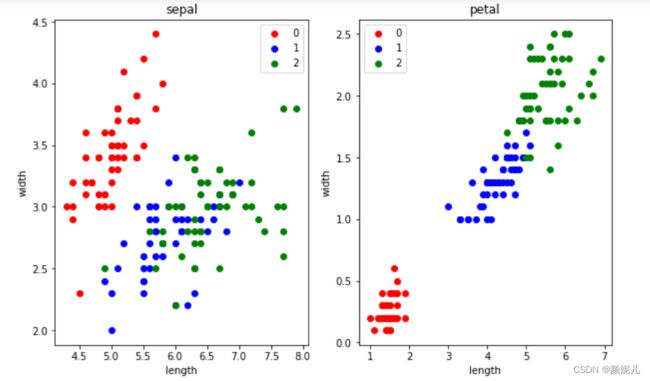
这里我没有去拿分的结果和本身的标签去看分的准确率,因为在实际的环境下,我们本身就拿不到标签~
但不难发现,kMeans算法是真的厉害!
测试代码:
/**
********************
* Test clustering.
*********************
*/
public static void testClustering() {
KMeans tempKMeans = new KMeans("F:/sampledataMain/iris.arff");
tempKMeans.setNumClusters(3);
tempKMeans.clustering();
}// Of testClustering
需求:获得虚拟中心后, 换成与其最近的点作为实际中心, 再聚类.
我定义了一个成员变量:
/**
* The nearest instances.
*/
int[] nearestInstances;
在clustering中进行初始化和更新值:
/**
********************
* Clustering.
*********************
*/
public void clustering() {
int[] tempOldClusterArray = new int[dataset.numInstances()];
tempOldClusterArray[0] = -1;
int[] tempClusterArray = new int[dataset.numInstances()];
Arrays.fill(tempClusterArray, 0);
double[][] tempCenters = new double[numClusters][dataset.numAttributes() - 1];
nearestInstances = new int[numClusters];
// Step 1. Initialize centers.
int[] tempRandomOrders = getRandomIndices(dataset.numInstances());
for (int i = 0; i < numClusters; i++) {
for (int j = 0; j < tempCenters[0].length; j++) {
tempCenters[i][j] = dataset.instance(tempRandomOrders[i]).value(j);
} // Of for j
nearestInstances[i] = tempRandomOrders[i];
} // Of for i
int[] tempClusterLengths = null;
while (!Arrays.equals(tempOldClusterArray, tempClusterArray)) {
System.out.println("New loop...");
tempOldClusterArray = tempClusterArray;
tempClusterArray = new int[dataset.numInstances()];
// Step 2.1 Minimization.Assign cluster to each instance.
int tempNearestCenter;
double tempNearestDistance;
double tempDistance = 0;
double[] tempMinDiffDistance = new double[numClusters];
for (int i = 0; i < numClusters; i++) {
tempMinDiffDistance[i] = Double.MAX_EXPONENT;
} // Of for i
for (int i = 0; i < dataset.numInstances(); i++) {
tempNearestCenter = -1;
tempNearestDistance = Double.MAX_VALUE;
for (int j = 0; j < numClusters; j++) {
tempDistance = distance(i, tempCenters[j]);
if (tempDistance < tempNearestDistance) {
tempNearestDistance = tempDistance;
tempNearestCenter = j;
} // Of if
} // Of for j
tempClusterArray[i] = tempNearestCenter;
// Update the nearest instance index.
if (tempDistance < tempMinDiffDistance[tempNearestCenter]) {
nearestInstances[tempNearestCenter] = i;
} // Of if
} // Of for i
// Step 2.2 Mean. Find new centers.
tempClusterLengths = new int[numClusters];
Arrays.fill(tempClusterLengths, 0);
double[][] tempNewCenters = new double[numClusters][dataset.numAttributes() - 1];
for (int i = 0; i < dataset.numInstances(); i++) {
for (int j = 0; j < tempNewCenters[0].length; j++) {
tempNewCenters[tempClusterArray[i]][j] += dataset.instance(i).value(j);
} // Of for j
tempClusterLengths[tempClusterArray[i]]++;
} // Of for i
// Step 2.3 Now average.
for (int i = 0; i < tempNewCenters.length; i++) {
for (int j = 0; j < tempNewCenters[0].length; j++) {
tempNewCenters[i][j] /= tempClusterLengths[i];
} // Of for j
} // Of for i
System.out.println("Now the new centers are: " + Arrays.deepToString(tempNewCenters));
tempCenters = tempNewCenters;
} // Of while
// Step 3. Form clusters.
clusters = new int[numClusters][];
int[] tempCounters = new int[numClusters];
for (int i = 0; i < numClusters; i++) {
clusters[i] = new int[tempClusterLengths[i]];
} // Of for i
for (int i = 0; i < tempClusterArray.length; i++) {
clusters[tempClusterArray[i]][tempCounters[tempClusterArray[i]]] = i;
tempCounters[tempClusterArray[i]]++;
} // Of for i
System.out.println("The clusters are: " + Arrays.deepToString(clusters));
}// Of clustering
再定义了一个根据实体样本划分簇的方法:
/**
********************
* Clustering with instance.
*********************
*/
public void clusteringWithInstance() {
int tempNearestCenter;
double tempNearestDistance;
double tempDistance = 0;
int[] tempClusterArray = new int[dataset.numInstances()];
int[] tempClusterLengths = new int[numClusters];
for (int i = 0; i < dataset.numInstances(); i++) {
tempNearestCenter = -1;
tempNearestDistance = Double.MAX_VALUE;
for (int j = 0; j < numClusters; j++) {
tempDistance = distance(i, nearestInstances[j]);
if (tempDistance < tempNearestDistance) {
tempNearestDistance = tempDistance;
tempNearestCenter = j;
} // Of if
} // Of for j
tempClusterArray[i] = tempNearestCenter;
tempClusterLengths[tempNearestCenter]++;
} // Of for i
clusters = new int[numClusters][];
int[] tempCounters = new int[numClusters];
for (int i = 0; i < numClusters; i++) {
clusters[i] = new int[tempClusterLengths[i]];
} // Of for i
for (int i = 0; i < tempClusterArray.length; i++) {
clusters[tempClusterArray[i]][tempCounters[tempClusterArray[i]]] = i;
tempCounters[tempClusterArray[i]]++;
} // Of for i
System.out.println("The clusters are: " + Arrays.deepToString(clusters));
}//Of clusteringWithInstance
更新测试代码:
/**
********************
* Test clustering.
*********************
*/
public static void testClustering() {
KMeans tempKMeans = new KMeans("F:/sampledataMain/iris.arff");
tempKMeans.setNumClusters(3);
tempKMeans.clustering();
tempKMeans.clusteringWithInstance();
}// Of testClustering
