一、Python的矩阵传播机制(Broadcasting)
我们知道在深度学习中经常要操作各种矩阵(matrix) 。回想一下,我们在操作数组(list)的时候,经常习惯于用**for循环(for-loop)**来对数组的每一个元素进行操作。例如:
my_list = [1,2,3,4] new_list = [] for each in my_list: new_list.append(each*2) print(new_list) # 输出 [2,3,4,5]
如果是矩阵呢:
my_matrix = [[1,2,3,4], [5,6,7,8]] new_matrix = [[],[]] for i in range(2): for j in range(4): new_matrix[i].append(my_matrix[i][j]*2) print(new_matrix)# 输出 [[2, 4, 6, 8], [10, 12, 14, 16]]
实际上,上面的做法是十分的低效的!数据量小的话还不明显,如果数据量大了,尤其是深度学习中我们处理的矩阵往往巨大,那用for循环去跑一个矩阵,可能要你几个小时甚至几天。
Python考虑到了这一点,这也是本文主要想介绍的**“Python的broadcasting”即传播机制**。
先说一句,python中定义矩阵、处理矩阵,我们一般都用numpy这个库。
二、下面展示什么是python的传播机制
import numpy as np# 先定义一个3×3矩阵 A:
A = np.array(
[[1,2,3],
[4,5,6],
[7,8,9]])
print("A:\n",A)
print("\nA*2:\n",A*2) # 直接用A乘以2
print("\nA+10:\n",A+10) # 直接用A加上10
运行结果:
A:
[[1 2 3]
[4 5 6]
[7 8 9]]A*2:
[[ 2 4 6]
[ 8 10 12]
[14 16 18]]A+10:
[[11 12 13]
[14 15 16]
[17 18 19]]
接着,再看看矩阵×(+)矩阵:
#定义一个3×1矩阵(此时也可叫向量了)
B = np.array([[10],
[100],
[1000]])
print("\nB:\n",B)
print("\nA+B:\n",A+B)
print("\nA*B:\n",A*B)
运行结果:
B:
[[ 10]
[ 100]
[1000]]A+B:
[[ 11 12 13]
[ 104 105 106]
[1007 1008 1009]]A*B:
[[ 10 20 30]
[ 400 500 600]
[7000 8000 9000]]
可见,虽然A和B的形状不一样,一个是3×3,一个是3×1,但是我们在python中可以直接相加、相乘,相减相除也可以。也许看到这,大家都对broadcasting有感觉了。
用一个图来示意一下:
所谓“传播”,就是把一个数或者一个向量进行“复制”,从而作用到矩阵的每一个元素上。
有了这种机制,那进行向量和矩阵的运算,就太方便了!理解了传播机制,就可以随心所欲地对矩阵进行各种便捷的操作了。
三、利用numpy的内置函数对矩阵进行操作
numpy内置了很多的数学函数,例如np.log(),np.abs(),np.maximum()等等上百种。直接把矩阵丢进去,就可以算出新矩阵! 示例:
print(np.log(A))
输出把A矩阵每一个元素求log后得到的新矩阵:
array([[0. , 0.69314718, 1.09861229], [1.38629436, 1.60943791, 1.79175947], [1.94591015, 2.07944154, 2.19722458]])
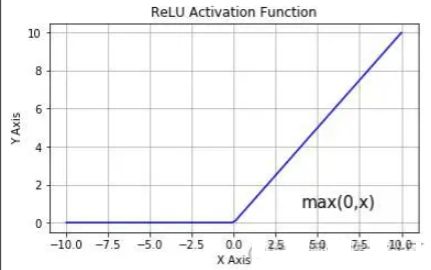
再比如深度学习中常用的ReLU激活函数,就是y=max(0,x),
也可以对矩阵直接运算:
X = np.array([[1,-2,3,-4], [-9,4,5,6]])Y = np.maximum(0,X)print(Y)
得到:
[[1 0 3 0] [0 4 5 6]]
更多的numpy数学函数,可以参见文档
四、定义自己的函数来处理矩阵
其实这才是我写下本文的目的。。。前面扯了这么多,只是做个铺垫( /ω\)
我昨天遇到个问题,就是我要对ReLU函数求导,易知,y=max(0,x)的导函数是:y’ = 0 if x<0 y’ = 1 if x>0 但是这个y’(x)numpy里面没有定义,需要自己构建。即,我需要将矩阵X中的小于0的元素变为0,大于0的元素变为1。搞了好久没弄出来,后来在StackOverflow上看到了解决办法:
def relu_derivative(x): x[x<0] = 0 x[x>0] = 1 return x X = np.array([[1,-2,3,-4], [-9,4,5,6]]) print(relu_derivative(X))
输出:
[[1 0 1 0]
[0 1 1 1]]
**居然这么简洁就出来了!!!**ミ゚Д゚彡 (゚Д゚#)
这个函数relu_derivative中最难以理解的地方,就是**x[x>0]**了。于是我试了一下:
X = np.array([[1,-2,3,-4], [-9,4,5,6]]) print(X[X>0]) print(X[X<0])
输出:
[1 3 4 5 6]
[-2 -4 -9]
它直接把矩阵X中满足条件的元素取了出来!原来python对矩阵还有这种操作!
所以可以这么理解,X[X>0]相当于一个“选择器”,把满足条件的元素选出来,然后直接全部赋值。
用这种方法,我们便可以定义各种各样我们需要的函数,然后对矩阵整体进行更新操作了!
五、总结
可以看出,python以及numpy对矩阵的操作简直神乎其神,方便快捷又实惠。其实上面忘了写一点,那就是计算机进行矩阵运算的效率要远远高于用for-loop来运算,
不信可以用跑一跑:
# vetorization vs for loop
# define two arrays a, b:
a = np.random.rand(1000000)
b = np.random.rand(1000000)
# for loop version:
t1 = time.time()
c = 0
for i in range(1000000):
c += a[i]*b[i]
t2 = time.time()
print(c)
print("for loop version:"+str(1000*(t2-t1))+"ms")
time1 = 1000*(t2-t1)
# vectorization version:
t1 = time.time()
c = np.dot(a,b)
t2 = time.time()
print(c)
print("vectorization version:"+str(1000*(t2-t1))+"ms")
time2 = 1000*(t2-t1)
print("vectorization is faster than for loop by "+str(time1/time2)+" times!")
运行结果:
249765.8415288075
for loop version:627.4442672729492ms
249765.84152880745
vectorization version:1.5032291412353516ms
vectorization is faster than for loop by 417.39762093576525 times!
可见,用for方法和向量化方法,计算结果是一样,但是后者比前者快了400多倍!
因此,在计算量很大的时候,我们要尽可能想办法对数据进行Vectorizing,即“向量化” ,以便让计算机进行矩阵运算。
到此这篇关于Python 的矩阵传播机制Broadcasting和矩阵运算的文章就介绍到这了,更多相关Python矩阵传播内容请搜索脚本之家以前的文章或继续浏览下面的相关文章希望大家以后多多支持脚本之家!