数学之美系列

数学之美 系列一 -- 统计语言模型

从本周开始，我们将定期刊登 Google 科学家吴军写的《数学之美》系列文章，介绍数学在信息检索和自然语言处理中的主导作用和奇妙应用。
发表者: 吴军, Google 研究员
前言
也许大家不相信，数学是解决信息检索和自然语言处理的最好工具。它能非常清晰地描述这些领域的实际问题并且给出漂亮的解决办法。每当人们应用数学工具解决一个语言问题时，总会感叹数学之美。我们希望利用 Google 中文黑板报这块园地，介绍一些数学工具，以及我们是如何利用这些工具来开发 Google 产品的。
系列一： 统计语言模型 (Statistical Language Models)
Google 的使命是整合全球的信息，所以我们一直致力于研究如何让机器对信息、语言做最好的理解和处理。长期以来，人类一直梦想着能让机器代替人来翻译语言、识别语音、认识文字（不论是印刷体或手写体）和进行海量文献的自动检索，这就需要让机器理解语言。但是人类的语言可以说是信息里最复杂最动态的一部分。为了解决这个问题，人们容易想到的办法就是让机器模拟人类进行学习 - 学习人类的语法、分析语句等等。尤其是在乔姆斯基（Noam Chomsky 有史以来最伟大的语言学家）提出 “形式语言” 以后，人们更坚定了利用语法规则的办法进行文字处理的信念。遗憾的是，几十年过去了，在计算机处理语言领域，基于这个语法规则的方法几乎毫无突破。
其实早在几十年前，数学家兼信息论的祖师爷 香农 (Claude Shannon)就提出了用数学的办法处理自然语言的想法。遗憾的是当时的计算机条件根本无法满足大量信息处理的需要，所以他这个想法当时并没有被人们重视。七十年代初，有了大规模集成电路的快速计算机后，香农的梦想才得以实现。
首先成功利用数学方法解决自然语言处理问题的是语音和语言处理大师贾里尼克 (Fred Jelinek)。当时贾里尼克在 IBM 公司做学术休假 (Sabbatical Leave)，领导了一批杰出的科学家利用大型计算机来处理人类语言问题。统计语言模型就是在那个时候提出的。
给大家举个例子：在很多涉及到自然语言处理的领域，如机器翻译、语音识别、印刷体或手写体识别、拼写纠错、汉字输入和文献查询中，我们都需要知道一个文字序列是否能构成一个大家能理解的句子，显示给使用者。对这个问题，我们可以用一个简单的统计模型来解决这个问题。
如果 S 表示一连串特定顺序排列的词 w1， w2，…， wn ，换句话说，S 可以表示某一个由一连串特定顺序排练的词而组成的一个有意义的句子。现在，机器对语言的识别从某种角度来说，就是想知道S在文本中出现的可能性，也就是数学上所说的S 的概率用 P(S) 来表示。利用条件概率的公式，S 这个序列出现的概率等于每一个词出现的概率相乘，于是P(S) 可展开为：
P(S) = P(w1)P(w2|w1)P(w3| w1 w2)…P(wn|w1 w2…wn-1)
其中 P (w1) 表示第一个词w1 出现的概率；P (w2|w1) 是在已知第一个词的前提下，第二个词出现的概率；以次类推。不难看出，到了词wn，它的出现概率取决于它前面所有词。从计算上来看，各种可能性太多，无法实现。因此我们假定任意一个词wi的出现概率只同它前面的词 wi-1 有关(即马尔可夫假设），于是问题就变得很简单了。现在，S 出现的概率就变为：
P(S) = P(w1)P(w2|w1)P(w3|w2)…P(wi|wi-1)…
(当然，也可以假设一个词又前面N-1个词决定，模型稍微复杂些。）
接下来的问题就是如何估计 P (wi|wi-1)。现在有了大量机读文本后，这个问题变得很简单，只要数一数这对词（wi-1,wi) 在统计的文本中出现了多少次，以及 wi-1 本身在同样的文本中前后相邻出现了多少次，然后用两个数一除就可以了,P(wi|wi-1) = P(wi-1,wi)/ P (wi-1)。
也许很多人不相信用这么简单的数学模型能解决复杂的语音识别、机器翻译等问题。其实不光是常人，就连很多语言学家都曾质疑过这种方法的有效性，但事实证明，统计语言模型比任何已知的借助某种规则的解决方法都有效。比如在 Google 的中英文自动翻译中，用的最重要的就是这个统计语言模型。去年美国标准局(NIST) 对所有的机器翻译系统进行了评测，Google 的系统是不仅是全世界最好的，而且高出所有基于规则的系统很多。
现在，读者也许已经能感受到数学的美妙之处了，它把一些复杂的问题变得如此的简单。当然，真正实现一个好的统计语言模型还有许多细节问题需要解决。贾里尼克和他的同事的贡献在于提出了统计语言模型，而且很漂亮地解决了所有的细节问题。十几年后，李开复用统计语言模型把 997 词语音识别的问题简化成了一个 20 词的识别问题，实现了有史以来第一次大词汇量非特定人连续语音的识别。
我是一名科学研究人员 ，我在工作中经常惊叹于数学语言应用于解决实际问题上时的神奇。我也希望把这种神奇讲解给大家听。当然，归根结底，不管什莫样的科学方法、无论多莫奇妙的解决手段都是为人服务的。我希望 Google 多努力一分，用户就多一分搜索的喜悦。

数学之美 系列二 -- 谈谈中文分词

----- 统计语言模型在中文处理中的一个应用
上回我们谈到利用统计语言模型进行语言处理，由于模型是建立在词的基础上的，对于中日韩等语言，首先需要进行分词。例如把句子 “中国航天官员应邀到美国与太空总署官员开会。”
分成一串词：
中国 / 航天 / 官员 / 应邀 / 到 / 美国 / 与 / 太空 / 总署 / 官员 / 开会。
最容易想到的，也是最简单的分词办法就是查字典。这种方法最早是由北京航天航空大学的梁南元教授提出的。
用 “查字典” 法，其实就是我们把一个句子从左向右扫描一遍，遇到字典里有的词就标识出来，遇到复合词（比如 “上海大学”）就找最长的词匹配，遇到不认识的字串就分割成单字词，于是简单的分词就完成了。这种简单的分词方法完全能处理上面例子中的句子。八十年代，哈工大的王晓龙博士把它理论化，发展成最少词数的分词理论，即一句话应该分成数量最少的词串。这种方法一个明显的不足是当遇到有二义性 （有双重理解意思）的分割时就无能为力了。比如，对短语 “发展中国家” 正确的分割是“发展-中-国家”，而从左向右查字典的办法会将它分割成“发展-中国-家”，显然是错了。另外，并非所有的最长匹配都一定是正确的。比如“上海大学城书店”的正确分词应该是 “上海-大学城-书店，” 而不是 “上海大学-城-书店”。
九十年代以前，海内外不少学者试图用一些文法规则来解决分词的二义性问题，都不是很成功。90年前后，清华大学的郭进博士用统计语言模型成功解决分词二义性问题，将汉语分词的错误率降低了一个数量级。
利用统计语言模型分词的方法，可以用几个数学公式简单概括如下：
我们假定一个句子S可以有几种分词方法，为了简单起见我们假定有以下三种：
A1, A2, A3, ..., Ak,
B1, B2, B3, ..., Bm
C1, C2, C3, ..., Cn
其中，A1, A2, B1, B2, C1, C2 等等都是汉语的词。那么最好的一种分词方法应该保证分完词后这个句子出现的概率最大。也就是说如果 A1,A2,..., Ak 是最好的分法，那么 （P 表示概率）：
P (A1, A2, A3, ..., Ak） 〉 P (B1, B2, B3, ..., Bm), 并且
P (A1, A2, A3, ..., Ak） 〉 P(C1, C2, C3, ..., Cn)
因此，只要我们利用上回提到的统计语言模型计算出每种分词后句子出现的概率，并找出其中概率最大的，我们就能够找到最好的分词方法。
当然，这里面有一个实现的技巧。如果我们穷举所有可能的分词方法并计算出每种可能性下句子的概率，那么计算量是相当大的。因此，我们可以把它看成是一个动态规划（Dynamic Programming) 的问题，并利用 “维特比”（Viterbi） 算法快速地找到最佳分词。
在清华大学的郭进博士以后，海内外不少学者利用统计的方法，进一步完善中文分词。其中值得一提的是清华大学孙茂松教授和香港科技大学吴德凯教授的工作。
需要指出的是，语言学家对词语的定义不完全相同。比如说 “北京大学”，有人认为是一个词，而有人认为该分成两个词。一个折中的解决办法是在分词的同时，找到复合词的嵌套结构。在上面的例子中，如果一句话包含“北京大学”四个字，那么先把它当成一个四字词，然后再进一步找出细分词 “北京” 和 “大学”。这种方法是最早是郭进在 “Computational Linguistics” （《计算机语言学》）杂志上发表的，以后不少系统采用这种方法。
一般来讲，根据不同应用，汉语分词的颗粒度大小应该不同。比如，在机器翻译中，颗粒度应该大一些，“北京大学”就不能被分成两个词。而在语音识别中，“北京大学”一般是被分成两个词。因此，不同的应用，应该有不同的分词系统。Google 的葛显平博士和朱安博士，专门为搜索设计和实现了自己的分词系统。
也许你想不到，中文分词的方法也被应用到英语处理，主要是手写体识别中。因为在识别手写体时，单词之间的空格就不很清楚了。中文分词方法可以帮助判别英语单词的边界。其实，语言处理的许多数学方法通用的和具体的语言无关。在 Google 内，我们在设计语言处理的算法时，都会考虑它是否能很容易地适用于各种自然语言。这样，我们才能有效地支持上百种语言的搜索。

数学之美 系列三 -- 隐含马尔可夫模型在语言处理中的应用

前言：隐含马尔可夫模型是一个数学模型，到目前为之，它一直被认为是实现快速精确的语音识别系统的最成功的方法。复杂的语音识别问题通过隐含马尔可夫模型能非常简单地被表述、解决，让我不由由衷地感叹数学模型之妙。
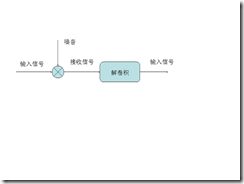
自然语言是人类交流信息的工具。很多自然语言处理问题都可以等同于通信系统中的解码问题 -- 一个人根据接收到的信息，去猜测发话人要表达的意思。这其实就象通信中，我们根据接收端收到的信号去分析、理解、还原发送端传送过来的信息。以下该图就表示了一个典型的通信系统：

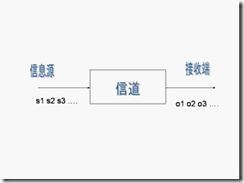
其中 s1，s2，s3...表示信息源发出的信号。o1, o2, o3 ... 是接受器接收到的信号。通信中的解码就是根据接收到的信号 o1, o2, o3 ...还原出发送的信号 s1，s2，s3...。
其实我们平时在说话时，脑子就是一个信息源。我们的喉咙（声带），空气，就是如电线和光缆般的信道。听众耳朵的就是接收端，而听到的声音就是传送过来的信号。根据声学信号来推测说话者的意思，就是语音识别。这样说来，如果接收端是一台计算机而不是人的话，那么计算机要做的就是语音的自动识别。同样，在计算机中，如果我们要根据接收到的英语信息，推测说话者的汉语意思，就是机器翻译； 如果我们要根据带有拼写错误的语句推测说话者想表达的正确意思，那就是自动纠错。
那么怎么根据接收到的信息来推测说话者想表达的意思呢？我们可以利用叫做“隐含马尔可夫模型”（Hidden Markov Model）来解决这些问题。以语音识别为例，当我们观测到语音信号 o1,o2,o3 时，我们要根据这组信号推测出发送的句子 s1,s2,s3。显然，我们应该在所有可能的句子中找最有可能性的一个。用数学语言来描述，就是在已知 o1,o2,o3,...的情况下，求使得条件概率
P (s1,s2,s3,...|o1,o2,o3....) 达到最大值的那个句子 s1,s2,s3,...
当然，上面的概率不容易直接求出，于是我们可以间接地计算它。利用贝叶斯公式并且省掉一个常数项，可以把上述公式等价变换成
P(o1,o2,o3,...|s1,s2,s3....) * P(s1,s2,s3,...)
其中
P(o1,o2,o3,...|s1,s2,s3....) 表示某句话 s1,s2,s3...被读成 o1,o2,o3,...的可能性, 而
P(s1,s2,s3,...) 表示字串 s1,s2,s3,...本身能够成为一个合乎情理的句子的可能性，所以这个公式的意义是用发送信号为 s1,s2,s3...这个数列的可能性乘以 s1,s2,s3...本身可以一个句子的可能性，得出概率。
（读者读到这里也许会问，你现在是不是把问题变得更复杂了，因为公式越写越长了。别着急，我们现在就来简化这个问题。）我们在这里做两个假设：
第一，s1,s2,s3,... 是一个马尔可夫链，也就是说，si 只由 si-1 决定 (详见系列一)；
第二， 第 i 时刻的接收信号 oi 只由发送信号 si 决定（又称为独立输出假设, 即 P(o1,o2,o3,...|s1,s2,s3....) = P(o1|s1) * P(o2|s2)*P(o3|s3)...。
那么我们就可以很容易利用算法 Viterbi 找出上面式子的最大值，进而找出要识别的句子 s1,s2,s3,...。
满足上述两个假设的模型就叫隐含马尔可夫模型。我们之所以用“隐含”这个词，是因为状态 s1,s2,s3,...是无法直接观测到的。
隐含马尔可夫模型的应用远不只在语音识别中。在上面的公式中，如果我们把 s1,s2,s3,...当成中文，把 o1,o2,o3,...当成对应的英文，那么我们就能利用这个模型解决机器翻译问题； 如果我们把 o1,o2,o3,...当成扫描文字得到的图像特征，就能利用这个模型解决印刷体和手写体的识别。
P (o1,o2,o3,...|s1,s2,s3....) 根据应用的不同而又不同的名称，在语音识别中它被称为“声学模型” (Acoustic Model)， 在机器翻译中是“翻译模型” (Translation Model) 而在拼写校正中是“纠错模型” (Correction Model)。 而P (s1,s2,s3,...) 就是我们在系列一中提到的语言模型。
在利用隐含马尔可夫模型解决语言处理问题前，先要进行模型的训练。 常用的训练方法由伯姆（Baum）在60年代提出的，并以他的名字命名。隐含马尔可夫模型在处理语言问题早期的成功应用是语音识别。七十年代，当时 IBM 的Fred Jelinek (贾里尼克) 和卡内基·梅隆大学的 Jim and Janet Baker(贝克夫妇，李开复的师兄师姐) 分别独立地提出用隐含马尔可夫模型来识别语音，语音识别的错误率相比人工智能和模式匹配等方法降低了三倍 (从 30% 到 10%)。 八十年代李开复博士坚持采用隐含马尔可夫模型的框架， 成功地开发了世界上第一个大词汇量连续语音识别系统 Sphinx。
我最早接触到隐含马尔可夫模型是几乎二十年前的事。那时在《随机过程》（清华“著名”的一门课）里学到这个模型，但当时实在想不出它有什么实际用途。几年后，我在清华跟随王作英教授学习、研究语音识别时，他给了我几十篇文献。 我印象最深的就是贾里尼克和李开复的文章，它们的核心思想就是隐含马尔可夫模型。复杂的语音识别问题居然能如此简单地被表述、解决，我由衷地感叹数学模型之妙。

数学之美系列 4 -- 怎样度量信息?

前言: Google 一直以 “整合全球信息，让人人能获取，使人人能受益” 为使命。那么究竟每一条信息应该怎样度量呢？
信息是个很抽象的概念。我们常常说信息很多，或者信息较少，但却很难说清楚信息到底有多少。比如一本五十万字的中文书到底有多少信息量。直到 1948 年，香农提出了“信息熵”(shāng) 的概念，才解决了对信息的量化度量问题。
一条信息的信息量大小和它的不确定性有直接的关系。比如说，我们要搞清楚一件非常非常不确定的事，或是我们一无所知的事情，就需要了解大量的信息。相反，如果我们对某件事已经有了较多的了解，我们不需要太多的信息就能把它搞清楚。所以，从这个角度，我们可以认为，信息量的度量就等于不确定性的多少。
那么我们如何量化的度量信息量呢？我们来看一个例子，马上要举行世界杯赛了。大家都很关心谁会是冠军。假如我错过了看世界杯，赛后我问一个知道比赛结果的观众“哪支球队是冠军”？ 他不愿意直接告诉我， 而要让我猜，并且我每猜一次，他要收一元钱才肯告诉我是否猜对了，那么我需要付给他多少钱才能知道谁是冠军呢? 我可以把球队编上号，从 1 到 32， 然后提问： “冠军的球队在 1-16 号中吗?” 假如他告诉我猜对了， 我会接着问： “冠军在 1-8 号中吗?” 假如他告诉我猜错了， 我自然知道冠军队在 9-16 中。 这样只需要五次， 我就能知道哪支球队是冠军。所以，谁是世界杯冠军这条消息的信息量只值五块钱。
当然，香农不是用钱，而是用 “比特”（bit）这个概念来度量信息量。 一个比特是一位二进制数，计算机中的一个字节是八个比特。在上面的例子中，这条消息的信息量是五比特。（如果有朝一日有六十四个队进入决赛阶段的比赛，那么“谁世界杯冠军”的信息量就是六比特，因为我们要多猜一次。） 读者可能已经发现, 信息量的比特数和所有可能情况的对数函数 log 有关。 (log32=5, log64=6。）
有些读者此时可能会发现我们实际上可能不需要猜五次就能猜出谁是冠军，因为象巴西、德国、意大利这样的球队得冠军的可能性比日本、美国、韩国等队大的多。因此，我们第一次猜测时不需要把 32 个球队等分成两个组，而可以把少数几个最可能的球队分成一组，把其它队分成另一组。然后我们猜冠军球队是否在那几只热门队中。我们重复这样的过程，根据夺冠概率对剩下的候选球队分组，直到找到冠军队。这样，我们也许三次或四次就猜出结果。因此，当每个球队夺冠的可能性（概率）不等时，“谁世界杯冠军”的信息量的信息量比五比特少。香农指出，它的准确信息量应该是
= -（p1*log p1 + p2 * log p2 +　．．．　＋p32 *log p32)，
其中，p1，p2 ，　．．．，p32 分别是这 32 个球队夺冠的概率。香农把它称为“信息熵” (Entropy)，一般用符号 H 表示，单位是比特。有兴趣的读者可以推算一下当 32 个球队夺冠概率相同时，对应的信息熵等于五比特。有数学基础的读者还可以证明上面公式的值不可能大于五。对于任意一个随机变量 X（比如得冠军的球队），它的熵定义如下：

变量的不确定性越大，熵也就越大，把它搞清楚所需要的信息量也就越大。
有了“熵”这个概念，我们就可以回答本文开始提出的问题，即一本五十万字的中文书平均有多少信息量。我们知道常用的汉字（一级二级国标）大约有 7000 字。假如每个字等概率，那么我们大约需要 13 个比特（即 13 位二进制数）表示一个汉字。但汉字的使用是不平衡的。实际上，前 10% 的汉字占文本的 95% 以上。因此，即使不考虑上下文的相关性，而只考虑每个汉字的独立的概率，那么，每个汉字的信息熵大约也只有 8-9 个比特。如果我们再考虑上下文相关性，每个汉字的信息熵只有5比特左右。所以，一本五十万字的中文书，信息量大约是 250 万比特。如果用一个好的算法压缩一下，整本书可以存成一个 320KB 的文件。如果我们直接用两字节的国标编码存储这本书，大约需要 1MB 大小，是压缩文件的三倍。这两个数量的差距，在信息论中称作“冗余度”（redundancy)。 需要指出的是我们这里讲的 250 万比特是个平均数，同样长度的书，所含的信息量可以差很多。如果一本书重复的内容很多，它的信息量就小，冗余度就大。
不同语言的冗余度差别很大，而汉语在所有语言中冗余度是相对小的。这和人们普遍的认识“汉语是最简洁的语言”是一致的。
在下一集中， 我们将介绍信息熵在信息处理中的应用以及两个相关的概念互信息和相对熵。
对中文信息熵有兴趣的读者可以读我和王作英教授在电子学报上合写的一篇文章
《语信息熵和语言模型的复杂度》

数学之美系列五 -- 简单之美：布尔代数和搜索引擎的索引

[建立一个搜索引擎大致需要做这样几件事：自动下载尽可能多的网页；建立快速有效的索引；根据相关性对网页进行公平准确的排序。我们在介绍 Google Page Rank (网页排名) 时已经谈到了一些排序的问题，这里我们谈谈索引问题，以后我们还会谈如何度量网页的相关性，和进行网页自动下载。］
世界上不可能有比二进制更简单的计数方法了，也不可能有比布尔运算更简单的运算了。尽管今天每个搜索引擎都宣称自己如何聪明、多么智能化，其实从根本上讲都没有逃出布尔运算的框框。
布尔（George Boole) 是十九世纪英国一位小学数学老师。他生前没有人认为他是数学家。布尔在工作之余，喜欢阅读数学论著、思考数学问题。1854 年“思维规律”（An Investigation of the Laws of Thought, on which are founded the Mathematical Theories of Logic and Probabilities）一书，第一次向人们展示了如何用数学的方法解决逻辑问题。
布尔代数简单得不能再简单了。运算的元素只有两个1 （TRUE， 真) 和 0
（FALSE，假)。基本的运算只有“与”（AND)、“或” (OR) 和“非”（NOT) 三种（后来发现，这三种运算都可以转换成“与”“非” ＡＮＤ－ＮＯＴ一种运算）。全部运算只用下列几张真值表就能完全地描述清楚。
AND | 1 0
-----------------------
1 | 1 0
0 | 0 0
这张表说明如果 AND 运算的两个元素有一个是 0，则运算结果总是 0。如果两个元素都是 1，运算结果是 1。例如，“太阳从西边升起”这个判断是假的(0),“水可以流动”这个判断是真的（1），那么，“太阳从西边升起并且水可以流动”就是假的（0）。
OR | 1 0
-----------------------
1 | 1 1
0 | 1 0
这张表说明如果OR运算的两个元素有一个是 1，则运算结果总是 1。如果两个元素都是 0，运算结果是 0。比如说，“张三是比赛第一名”这个结论是假的（0），“李四是比赛第一名”是真的（1），那么“张三或者李四是第一名”就是真的（1）。
NOT |
--------------
1 | 0
0 | 1
这张表说明 NOT 运算把 1 变成 0，把 0 变成 1。比如，如果“象牙是白的”是真的（1），那么“象牙不是白的”必定是假的（0）。
读者也许会问这么简单的理论能解决什么实际问题。布尔同时代的数学家们也有同样的问题。事实上在布尔代数提出后80 多年里，它确实没有什么像样的应用，直到 1938 年香农在他的硕士论文中指出用布尔代数来实现开关电路，才使得布尔代数成为数字电路的基础。所有的数学和逻辑运算，加、减、乘、除、乘方、开方等等，全部能转换成二值的布尔运算。
现在我们看看文献检索和布尔运算的关系。对于一个用户输入的关键词，搜索引擎要判断每篇文献是否含有这个关键词，如果一篇文献含有它，我们相应地给这篇文献一个逻辑值 -- 真（TRUE,或 1），否则，给一个逻辑值 -- 假（FALSE, 或0）。比如我们要找有关原子能应用的文献，但并不想知道如何造原子弹。我们可以这样写一个查询语句“原子能 AND 应用 AND (NOT 原子弹)”，表示符合要求的文献必须同时满足三个条件：
- 包含原子能
- 包含应用
- 不包含原子弹
一篇文献对于上面每一个条件，都有一个 True 或者 False 的答案，根据上述真值表就能算出每篇文献是否是要找的。
早期的文献检索查询系统大多基于数据库，严格要求查询语句符合布尔运算。今天的搜索引擎相比之下要聪明的多，它自动把用户的查询语句转换成布尔运算的算式。当然在查询时，不能将每篇文献扫描一遍，来看看它是否满足上面三个条件，因此需要建立一个索引。
最简单索引的结构是用一个很长的二进制数表示一个关键字是否出现在每篇文献中。有多少篇文献，就有多少位数，每一位对应一篇文献，1 代表相应的文献有这个关键字，0 代表没有。比如关键字“原子能”对应的二进制数是0100100001100001...，表示第二、第五、第九、第十、第十六篇文献包含着个关键字。注意，这个二进制数非常之长。同样，我们假定“应用”对应的二进制数是 0010100110000001...。那么要找到同时包含“原子能”和“应用”的文献时，只要将这两个二进制数进行布尔运算 AND。根据上面的真值表，我们知道运算结果是0000100000000001...。表示第五篇，第十六篇文献满足要求。
注意，计算机作布尔运算是非常非常快的。现在最便宜的微机都可以一次进行三十二位布尔运算，一秒钟进行十亿次以上。当然，由于这些二进制数中绝大部分位数都是零，我们只需要记录那些等于1的位数即可。于是，搜索引擎的索引就变成了一张大表：表的每一行对应一个关键词，而每一个关键词后面跟着一组数字，是包含该关键词的文献序号。
对于互联网的搜索引擎来讲，每一个网页就是一个文献。互联网的网页数量是巨大的，网络中所用的词也非常非常多。因此这个索引是巨大的，在万亿字节这个量级。早期的搜索引擎（比如 Alta Vista 以前的所有搜索引擎），由于受计算机速度和容量的限制，只能对重要的关键的主题词建立索引。至今很多学术杂志还要求作者提供 3-5 个关键词。这样所有不常见的词和太常见的虚词就找不到了。现在，为了保证对任何搜索都能提供相关的网页，所有的搜索引擎都是对所有的词进行索引。为了网页排名方便，索引中还需存有大量附加信息，诸如每个词出现的位置、次数等等。因此，整个索引就变得非常之大，以至于不可能用一台计算机存下。大家普遍的做法就是根据网页的序号将索引分成很多份（Shards)，分别存储在不同的服务器中。每当接受一个查询时，这个查询就被分送到许许多多服务器中，这些服务器同时并行处理用户请求，并把结果送到主服务器进行合并处理，最后将结果返回给用户。
不管索引如何复杂，查找的基本操作仍然是布尔运算。布尔运算把逻辑和数学联系起来了。它的最大好处是容易实现，速度快，这对于海量的信息查找是至关重要的。它的不足是只能给出是与否的判断，而不能给出量化的度量。因此，所有搜索引擎在内部检索完毕后，都要对符合要求的网页根据相关性排序，然后才返回给用户。

数学之美系列六 -- 图论和网络爬虫 (Web Crawlers)

[离散数学是当代数学的一个重要分支，也是计算机科学的数学基础。它包括数理逻辑、集合论、图论和近世代数四个分支。数理逻辑基于布尔运算，我们已经介绍过了。这里我们介绍图论和互联网自动下载工具网络爬虫 (Web Crawlers) 之间的关系。顺便提一句，我们用Google Trends 来搜索一下“离散数学”这个词，可以发现不少有趣的现象。比如，武汉、哈尔滨、合肥和长沙市对这一数学题目最有兴趣的城市。]
我们上回谈到了如何建立搜索引擎的索引，那么如何自动下载互联网所有的网页呢，它要用到图论中的遍历（Traverse) 算法。
图论的起源可追溯到大数学家欧拉（Leonhard Euler）。1736 年欧拉来到德国的哥尼斯堡（Konigsberg，大哲学家康德的故乡，现在是俄罗斯的加里宁格勒），发现当地市民们有一项消遣活动，就是试图将下图中的每座桥恰好走过一遍并回到原出发点，从来没有人成功过。欧拉证明了这件事是不可能的，并写了一篇论文，一般认为这是图论的开始。

图论中所讨论的的图由一些节点和连接这些节点的弧组成。如果我们把中国的城市当成节点，连接城市的国道当成弧，那么全国的公路干线网就是图论中所说的图。关于图的算法有很多，但最重要的是图的遍历算法，也就是如何通过弧访问图的各个节点。以中国公路网为例，我们从北京出发，看一看北京和哪些城市直接相连，比如说和天津、济南、石家庄、南京、沈阳、大同直接相连。我们可以依次访问这些城市，然后我们看看都有哪些城市和这些已经访问过的城市相连，比如说北戴河、秦皇岛与天津相连，青岛、烟台和济南相连，太原、郑州和石家庄相连等等，我们再一次访问北戴河这些城市，直到中国所有的城市都访问过一遍为止。这种图的遍历算法称为“广度优先算法”（BFS)，因为它先要尽可能广地访问每个节点所直接连接的其他节点。另外还有一种策略是从北京出发，随便找到下一个要访问的城市，比如是济南，然后从济南出发到下一个城市，比如说南京，再访问从南京出发的城市，一直走到头。然后再往回找，看看中间是否有尚未访问的城市。这种方法叫“深度优先算法”（DFS)，因为它是一条路走到黑。这两种方法都可以保证访问到全部的城市。当然，不论采用哪种方法，我们都应该用一个小本本，记录已经访问过的城市，以防同一个城市访问多次或者漏掉哪个城市。
现在我们看看图论的遍历算法和搜索引擎的关系。互联网其实就是一张大图，我们可以把每一个网页当作一个节点，把那些超链接（Hyperlinks)当作连接网页的弧。很多读者可能已经注意到，网页中那些蓝色的、带有下划线的文字背后其实藏着对应的网址，当你点下去的的时候，浏览器是通过这些隐含的网址转到相应的网页中的。这些隐含在文字背后的网址称为“超链接”。有了超链接，我们可以从任何一个网页出发，用图的遍历算法，自动地访问到每一个网页并把它们存起来。完成这个功能的程序叫做网络爬虫，或者在一些文献中称为"机器人"（Robot)。世界上第一个网络爬虫是由麻省理工学院 (MIT)的学生马休.格雷（Matthew Gray)在 1993 年写成的。他给他的程序起了个名字叫“互联网漫游者”("www wanderer")。以后的网络爬虫越写越复杂，但原理是一样的。
我们来看看网络爬虫如何下载整个互联网。假定我们从一家门户网站的首页出发，先下载这个网页，然后通过分析这个网页，可以找到藏在它里面的所有超链接，也就等于知道了这家门户网站首页所直接连接的全部网页，诸如雅虎邮件、雅虎财经、雅虎新闻等等。我们接下来访问、下载并分析这家门户网站的邮件等网页，又能找到其他相连的网页。我们让计算机不停地做下去，就能下载整个的互联网。当然，我们也要记载哪个网页下载过了，以免重复。在网络爬虫中，我们使用一个称为“哈希表”(Hash Table)的列表而不是一个记事本纪录网页是否下载过的信息。
现在的互联网非常巨大，不可能通过一台或几台计算机服务器就能完成下载任务。比如雅虎公司（Google 没有公开公布我们的数目，所以我这里举了雅虎的索引大小为例）宣称他们索引了 200 亿个网页，假如下载一个网页需要一秒钟，下载这 200 亿个网页则需要 634 年。因此，一个商业的网络爬虫需要有成千上万个服务器，并且由快速网络连接起来。如何建立这样复杂的网络系统，如何协调这些服务器的任务，就是网络设计和程序设计的艺术了。

数学之美 系列七 -- 信息论在信息处理中的应用

我们已经介绍了信息熵，它是信息论的基础，我们这次谈谈信息论在自然语言处理中的应用。
先看看信息熵和语言模型的关系。我们在系列一中谈到语言模型时，没有讲如何定量地衡量一个语言模型的好坏，当然，读者会很自然地想到，既然语言模型能减少语音识别和机器翻译的错误，那么就拿一个语音识别系统或者机器翻译软件来试试，好的语言模型必然导致错误率较低。这种想法是对的，而且今天的语音识别和机器翻译也是这么做的。但这种测试方法对于研发语言模型的人来讲，既不直接、又不方便，而且很难从错误率反过来定量度量语言模型。事实上，在贾里尼克(Fred Jelinek)的人研究语言模型时，世界上既没有像样的语音识别系统，更没有机器翻译。我们知道，语言模型是为了用上下文预测当前的文字，模型越好，预测得越准，那么当前文字的不确定性就越小。
信息熵正是对不确定性的衡量，因此信息熵可以直接用于衡量统计语言模型的好坏。贾里尼克从信息熵出发，定义了一个称为语言模型复杂度(Perplexity)的概念，直接衡量语言模型的好坏。一个模型的复杂度越小，模型越好。李开复博士在介绍他发明的 Sphinx 语音识别系统时谈到，如果不用任何语言模型（即零元语言模型）时，复杂度为997，也就是说句子中每个位置有 997 个可能的单词可以填入。如果（二元）语言模型只考虑前后词的搭配不考虑搭配的概率时，复杂度为 60。虽然它比不用语言模型好很多，但是和考虑了搭配概率的二元语言模型相比要差很多，因为后者的复杂度只有 20。
信息论中仅次于熵的另外两个重要的概念是“互信息”（Mutual Information) 和“相对熵”（Kullback-Leibler Divergence)。
“互信息”是信息熵的引申概念，它是对两个随机事件相关性的度量。比如说今天随机事件北京下雨和随机变量空气湿度的相关性就很大，但是和姚明所在的休斯敦火箭队是否能赢公牛队几乎无关。互信息就是用来量化度量这种相关性的。在自然语言处理中，经常要度量一些语言现象的相关性。比如在机器翻译中，最难的问题是词义的二义性（歧义性）问题。比如 Bush 一词可以是美国总统的名字，也可以是灌木丛。（有一个笑话，美国上届总统候选人凯里 Kerry 的名字被一些机器翻译系统翻译成了"爱尔兰的小母牛"，Kerry 在英语中另外一个意思。）那么如何正确地翻译这个词呢？人们很容易想到要用语法、要分析语句等等。其实，至今为止，没有一种语法能很好解决这个问题，真正实用的方法是使用互信息。具体的解决办法大致如下：首先从大量文本中找出和总统布什一起出现的互信息最大的一些词，比如总统、美国、国会、华盛顿等等，当然，再用同样的方法找出和灌木丛一起出现的互信息最大的词，比如土壤、植物、野生等等。有了这两组词，在翻译 Bush 时，看看上下文中哪类相关的词多就可以了。这种方法最初是由吉尔(Gale)，丘奇(Church)和雅让斯基(Yarowsky)提出的。
当时雅让斯基在宾西法尼亚大学是自然语言处理大师马库斯 (Mitch Marcus) 教授的博士生，他很多时间泡在贝尔实验室丘奇等人的研究室里。也许是急于毕业，他在吉尔等人的帮助下想出了一个最快也是最好地解决翻译中的二义性，就是上述的方法，这个看上去简单的方法效果好得让同行们大吃一惊。雅让斯基因而只花了三年就从马库斯那里拿到了博士，而他的师兄弟们平均要花六年时间。
信息论中另外一个重要的概念是“相对熵”，在有些文献中它被称为成“交叉熵”。在英语中是 Kullback-Leibler Divergence，是以它的两个提出者库尔贝克和莱伯勒的名字命名的。相对熵用来衡量两个正函数是否相似，对于两个完全相同的函数，它们的相对熵等于零。在自然语言处理中可以用相对熵来衡量两个常用词（在语法上和语义上）是否同义，或者两篇文章的内容是否相近等等。利用相对熵，我们可以到处信息检索中最重要的一个概念：词频率-逆向文档频率（TF/IDF)。我们下回会介绍如何根据相关性对搜索出的网页进行排序，就要用的餐TF/IDF 的概念。另外，在新闻的分类中也要用到相对熵和 TF/IDF。
对信息论有兴趣又有一定数学基础的读者，可以阅读斯坦福大学托马斯.科弗 (Thomas Cover) 教授的专著 "信息论基础"(Elements of Information Theory)：

数学之美 系列八-- 贾里尼克的故事和现代语言处理

读者也许注意到了，我们在前面的系列中多次提到了贾里尼克这个名字。事实上，现代语音识别和自然语言处理确实是和它的名字是紧密联系在一起的。我想在这回的系列里，介绍贾里尼克本人。在这里我不想列举他的贡献，而想讲一讲他作为一个普普通通的人的故事。这些事要么是我亲身经历的，要么是他亲口对我讲的。
弗莱德里克.贾里尼克(Fred Jelinek)出生于捷克一个富有的犹太家庭。他的父母原本打算送他去英国的公学（私立学校）读书。为了教他德语，还专门请的一位德国的家庭女教师，但是第二次世界大战完全打碎了他们的梦想。他们先是被从家中赶了出去，流浪到布拉格。他的父亲死在了集中营，弗莱德自己成天在街上玩耍，完全荒废了学业。二战后，当他再度回到学校时，他的成绩一塌糊涂， 全部是 D，但是很快他就赶上了班上的同学。不过，他在小学时从来没有得过 A。1949年，他的母亲带领全家移民美国。在美国，贾里尼克一家生活非常贫困，全家基本是靠母亲做点心卖钱为生，弗莱德自己十四五岁就进工厂打工补助全家。
贾里尼克最初想成为一个律师，为他父亲那样的冤屈者辩护，但他很快意识到他那浓厚的外国口音将使他在法庭上的辩护很吃力。贾里尼克的第二个理想是成为医生，他想进哈佛大学医学院，但经济上他无法承担医学院 8 年高昂的学费。与此同时麻省理工学院给于了他一份（为东欧移民设的）全额奖学金。贾里尼克决定到麻省理工学电机工程。在那里，他遇到了信息论的鼻祖香农博士，和语言学大师贾格布森Roman Jakobson (他提出了著名的通信六功能）[注释一]，后来贾里尼克又陪着太太听最伟大的语言学家乔姆斯基(Noam Chomsky)的课。这三位大师对贾里尼克今后的研究方向--利用信息论解决语言问题产生的重要影响。
贾里尼克从麻省理工获得博士学位后，在哈佛大学教了一年书，然后到康乃尔大学任教。他之所以选择康乃尔大学，是因为找工作时和那里的一位语言学家谈得颇为投机。当时那位教授表示愿意和贾里尼克在利用信息论解决语言问题上合作。但是，等贾里尼克到康乃尔以后，那位教授表示对语言学在没有兴趣而转向写歌剧了。贾里尼克对语言学家的坏印象从此开始。加上后来他在 IBM 时发现语言学家们嘴上头头是道，干起活来高不成低不就，对语言学家从此深恶痛绝。他甚至说："我每开除一名语言学家，我的语音识别系统错误率就降低一个百分点。" 这句话后来在业界广为流传，为每一个搞语音识别和语言处理的人所熟知。
贾里尼克在康乃尔十年磨一剑，潜心研究信息论，终于悟出了自然语言处理的真谛。１９７２年，贾里尼克到ＩＢＭ 华生实验室（ＩＢＭ　Ｔ．Ｇ．Ｗａｔｓｏｎ　Ｌａｂｓ）做学术休假，无意中领导了语音识别实验室，两年后他在康乃尔和ＩＢＭ 之间选择了留在ＩＢＭ。在那里，贾里尼克组建了阵容空前绝后强大的研究队伍，其中包括他的著名搭档波尔（Bahl），著名的语音识别 Dragon 公司的创始人贝克夫妇，解决最大熵迭代算法的达拉皮垂(Della Pietra)孪生兄弟，BCJR 算法的另外两个共同提出者库克(Cocke)和拉维夫(Raviv)，以及第一个提出机器翻译统计模型的布朗。
七十年代的 IBM 有点像九十年代的微软和今天的 Google, 给于杰出科学家作任何有兴趣研究的自由。在那种宽松的环境里，贾里尼克等人提出了统计语音识别的框架结构。 在贾里尼克以前，科学家们把语音识别问题当作人工智能问题和模式匹配问题。而贾里尼克把它当成通信问题，并用两个隐含马尔可夫模型（声学模型和语言模型）把语音识别概括得清清楚楚。这个框架结构对至今的语音和语言处理有着深远的影响，它从根本上使得语音识别有实用的可能。 贾里尼克本人后来也因此当选美国工程院院士。
贾里尼克和波尔，库克以及拉维夫对人类的另一大贡献是 BCJR 算法，这是今天数字通信中应用的最广的两个算法之一（另一个是维特比算法）。有趣的是，这个算法发明了二十年后，才得以广泛应用。IBM 于是把它列为了 IBM 有史以来对人类最大贡献之一，并贴在加州 Amaden 实现室墙上。遗憾的是 BCJR 四个人已经全部离开 IBM，有一次IBM 的通信部门需要用这个算法，还得从斯坦福大学请一位专家去讲解，这位专家看到 IBM 橱窗里的成就榜，感慨万分。
贾里尼克和 IBM 一批最杰出的科学家在九十年代初离开了 IBM，他们大多数在华尔街取得了巨大的成功。贾里尼克的书生气很浓，于是去约翰霍普金斯大学建立了世界著名的 CLSP 实验室。每年夏天，贾里尼克邀请世界上 20-30 名顶级的科学家和学生到 CLSP 一起工作，使得 CLSP 成为世界上语音和语言处理的中心之一。
贾里尼克治学极为严谨，对学生要求也极严。他淘汰学生的比例极高，即使留下来的，毕业时间也极长。但是，另一方面，贾里尼克也千方百计利用自己的影响力为学生的学习和事业创造方便。贾里尼克为组里的每一位学生提供从进组第一天到离开组最后一天全部的学费和生活费。他还为每一位学生联系实习机会，并保证每位学生在博士生阶段至少在大公司实习一次。从他那里拿到博士学位的学生，全部任职于著名实验室，比如IBM, 微软，AT&T 和 Google 的实验室。为了提高外国人的英语水平，贾里尼克用自己的经费为他们请私人英语教师。
贾里尼克生活俭朴，一辆老式丰田车开了二十多年，比组里学生的车都破。他每年都邀请组里的学生和教授到家里做客，很多毕业了的学生也专程赶来聚会。在那里，他不再谈论学术问题，而会谈些巩俐的电影（他太太是哥伦比亚大学电影专业的教授），或是某著名教授被拉斯韦加斯的赌馆定为不受欢迎的人等等。但是他聚会的食物实在难吃，无非是些生胡萝卜和芹菜。后来贾里尼克掏钱让系里另一个教授承办聚会，那个教授每次请专业大厨在家作出极丰盛的晚宴，并准备许多美酒，从此这种聚会就转移到那个教授家了。
除了巩俐的电影，贾里尼克对中国的了解就是清华大学和青岛啤酒了。他有时会把两个名字搞混，有两次被香港科技大学的 Pascale 冯教授抓住。
贾里尼克说话心直口快，不留余地。在他面前谈论学术一定要十分严谨，否则很容易被他抓住辫子。除了刚才提到的对语言学家略有偏见的评论，他对许多世界级的大师都有过很多“刻薄”但又实事求是的评论，这些评论在业界广为流传。贾里尼克在四十多年的学术生涯中居然没有得罪太多的人 ，可以说是一个奇迹。

数学之美 系列九 -- 如何确定网页和查询的相关性

[我们已经谈过了如何自动下载网页、如何建立索引、如何衡量网页的质量(Page Rank)。我们今天谈谈如何确定一个网页和某个查询的相关性。了解了这四个方面，一个有一定编程基础的读者应该可以写一个简单的搜索引擎了，比如为您所在的学校或院系建立一个小的搜索引擎。]
我们还是看上回的例子，查找关于“原子能的应用”的网页。我们第一步是在索引中找到包含这三个词的网页（详见关于布尔运算的系列）。现在任何一个搜索引擎都包含几十万甚至是上百万个多少有点关系的网页。那么哪个应该排在前面呢？显然我们应该根据网页和查询“原子能的应用”的相关性对这些网页进行排序。因此，这里的关键问题是如何度量网页和查询的相关性。
我们知道，短语“原子能的应用”可以分成三个关键词：原子能、的、应用。根据我们的直觉，我们知道，包含这三个词多的网页应该比包含它们少的网页相关。当然，这个办法有一个明显的漏洞，就是长的网页比短的网页占便宜，因为长的网页总的来讲包含的关键词要多些。因此我们需要根据网页的长度，对关键词的次数进行归一化，也就是用关键词的次数除以网页的总字数。我们把这个商称为“关键词的频率”，或者“单文本词汇频率”（Term Frequency)，比如，在某个一共有一千词的网页中“原子能”、“的”和“应用”分别出现了 2 次、35 次 和 5 次，那么它们的词频就分别是 0.002、0.035 和 0.005。 我们将这三个数相加，其和 0.042 就是相应网页和查询“原子能的应用”
相关性的一个简单的度量。概括地讲，如果一个查询包含关键词 w1,w2,...,wN, 它们在一篇特定网页中的词频分别是: TF1, TF2, ..., TFN。 （TF: term frequency)。 那么，这个查询和该网页的相关性就是:
TF1 + TF2 + ... + TFN。
读者可能已经发现了又一个漏洞。在上面的例子中，词“的”站了总词频的 80% 以上，而它对确定网页的主题几乎没有用。我们称这种词叫“应删除词”（Stopwords)，也就是说在度量相关性是不应考虑它们的频率。在汉语中，应删除词还有“是”、“和”、“中”、“地”、“得”等等几十个。忽略这些应删除词后，上述网页的相似度就变成了0.007，其中“原子能”贡献了0.002，“应用”贡献了 0.005。
细心的读者可能还会发现另一个小的漏洞。在汉语中，“应用”是个很通用的词，而“原子能”是个很专业的词，后者在相关性排名中比前者重要。因此我们需要给汉语中的每一个词给一个权重，这个权重的设定必须满足下面两个条件：
1. 一个词预测主题能力越强，权重就越大，反之，权重就越小。我们在网页中看到“原子能”这个词，或多或少地能了解网页的主题。我们看到“应用”一次，对主题基本上还是一无所知。因此，“原子能“的权重就应该比应用大。
2. 应删除词的权重应该是零。
我们很容易发现，如果一个关键词只在很少的网页中出现，我们通过它就容易锁定搜索目标，它的权重也就应该大。反之如果一个词在大量网页中出现，我们看到它仍然不很清楚要找什么内容，因此它应该小。概括地讲，假定一个关键词 ｗ 在 Ｄｗ 个网页中出现过，那么 Ｄｗ 越大，ｗ 的权重越小，反之亦然。在信息检索中，使用最多的权重是“逆文本频率指数” （Inverse document frequency 缩写为ＩＤＦ），它的公式为ｌｏｇ（Ｄ／Ｄｗ）其中Ｄ是全部网页数。比如，我们假定中文网页数是Ｄ＝１０亿，应删除词“的”在所有的网页中都出现，即Ｄｗ＝１０亿，那么它的ＩＤＦ＝log(10亿/10亿）= log (1) = ０。假如专用词“原子能”在两百万个网页中出现，即Ｄｗ＝２００万，则它的权重ＩＤＦ＝log(500) =6.2。又假定通用词“应用”，出现在五亿个网页中，它的权重ＩＤＦ = log(2)
则只有 0.7。也就只说，在网页中找到一个“原子能”的比配相当于找到九个“应用”的匹配。利用 IDF，上述相关性计算个公式就由词频的简单求和变成了加权求和，即 TF1*IDF1 + TF2*IDF2 ＋... + TFN*IDFN。在上面的例子中，该网页和“原子能的应用”的相关性为 0.0161，其中“原子能”贡献了 0.0126，而“应用”只贡献了0.0035。这个比例和我们的直觉比较一致了。
ＴＦ／ＩＤＦ（term frequency/inverse document frequency) 的概念被公认为信息检索中最重要的发明。在搜索、文献分类和其他相关领域有广泛的应用。讲起 TF/IDF 的历史蛮有意思。IDF 的概念最早是剑桥大学的斯巴克－琼斯[注：她有两个姓］ (Karen Sparck Jones)提出来的。斯巴克－琼斯 １９７２ 年在一篇题为关键词特殊性的统计解释和她在文献检索中的应用的论文中提出ＩＤＦ。遗憾的是，她既没有从理论上解释为什么权重ＩＤＦ 应该是对数函数 ｌｏｇ（Ｄ／Ｄｗ）（而不是其它的函数，比如平方根），也没有在这个题目上作进一步深入研究，以至于在以后的很多文献中人们提到 ＴＦ／ＩＤＦ 时没有引用她的论文，绝大多数人甚至不知道斯巴克－琼斯的贡献。同年罗宾逊写了个两页纸的解释，解释得很不好。倒是后来康乃尔大学的萨尔顿（Salton)多次写文章、写书讨论 TF/IDF 在信息检索中的用途，加上萨尔顿本人的大名（信息检索的世界大奖就是以萨尔顿的名字命名的）。很多人都引用萨尔顿的书，甚至以为这个信息检索中最重要的概念是他提出的。当然，世界并没有忘记斯巴克－琼斯的贡献，2004年，在纪念文献学学报创刊 60 周年之际，该学报重印了斯巴克-琼斯的大作。罗宾逊在同期期刊上写了篇文章，用香农的信息论解释 IDF，这回的解释是对的，但文章写的并不好、非常冗长（足足十八页），把一个简单问题搞复杂了。其实，信息论的学者们已经发现并指出，其实 IDF 的概念就是一个特定条件下、关键词的概率分布的交叉熵（Kullback-Leibler Divergence)（详见上一系列）。这样，信息检索相关性的度量，又回到了信息论。
现在的搜索引擎对 TF/IDF 进行了不少细微的优化，使得相关性的度量更加准确了。当然，对有兴趣写一个搜索引擎的爱好者来讲，使用 TF/IDF 就足够了。 如果我们结合上网页排名(Page Rank)，那么给定一个查询，有关网页综合排名大致由相关性和网页排名乘积决定。

数学之美 系列十 有限状态机和地址识别

地址的识别和分析是本地搜索必不可少的技术，尽管有许多识别和分析地址的方法，最有效的是有限状态机。
一个有限状态机是一个特殊的有向图（参见有关图论的系列），它包括一些状态（节点）和连接这些状态的有向弧。下图是一个识别中国地址的有限状态机的简单的例子。

每一个有限状态机都有一个启始状态和一个终止状态和若干中间状态。每一条弧上带有从一个状态进入下一个状态的条件。比如，在上图中，当前的状态是“省”，如果遇到一个词组和（区）县名有关，我们就进入状态“区县”；如果遇到的下一个词组和城市有关，那么我们就进入“市”的状态，如此等等。如果一条地址能从状态机的起始状态经过状态机的若干中间状态，走到终止状态，那么这条地址则有效，否则无效。比如说，“北京市双清路83号”对于上面的有限状态来讲有效，而“上海市辽宁省马家庄”则无效（因为无法从市走回到省）。
使用有限状态机识别地址，关键要解决两个问题，即通过一些有效的地址建立状态机，以及给定一个有限状态机后，地址字串的匹配算法。好在这两个问题都有现成的算法。有了关于地址的有限状态机后，我们就可又用它分析网页，找出网页中的地址部分，建立本地搜索的数据库。同样，我们也可以对用户输入的查询进行分析，挑出其中描述地址的部分，当然，剩下的关键词就是用户要找的内容。比如，对于用户输入的“北京市双清路附近的酒家”，Google 本地会自动识别出地址“北京市双清路”和要找的对象“酒家”。
上述基于有限状态机的地址识别方法在实用中会有一些问题：当用户输入的地址不太标准或者有错别字时，有限状态机会束手无策，因为它只能进行严格匹配。（其实，有限状态机在计算机科学中早期的成功应用是在程序语言编译器的设计中。一个能运行的程序在语法上必须是没有错的，所以不需要模糊匹配。而自然语言则很随意，无法用简单的语法描述。）
为了解决这个问题，我们希望有一个能进行模糊匹配、并给出一个字串为正确地址的可能性。为了实现这一目的，科学家们提出了基于概率的有限状态机。这种基于概率的有限状态机和离散的马尔可夫链（详见前面关于马尔可夫模型的系列）基本上等效。
在八十年代以前，尽管有不少人使用基于概率的有限状态机，但都是为自己的应用设计专用的有限状态机的程序。九十年代以后，随着有限状态机在自然语言处理的广泛应用，不少科学家致力于编写通用的有限状态机程序库。其中，最成功的是前 AT&T 实验室的三位科学家，莫瑞（Mohri）, 皮瑞尔（Pereira） 和瑞利（Riley）。他们三人花了很多年时间，编写成一个通用的基于概率的有限状态机 C 语言工具库。由于 AT&T 有对学术界免费提供各种编程工具的好传统，他们三人也把自己多年的心血拿出来和同行们共享。可惜好景不长，AT&T 实验室风光不再，这三个人都离开了 AT&T，莫瑞成了纽约大学的教授，皮瑞尔当了宾西法尼亚大学计算机系系主任，而瑞利成了 Google 的研究员，AT&T 实验室的新东家不再免费提供有限状态机 C 语言工具库。虽然此前莫瑞等人公布了他们的详细算法，但是省略了实现的细节。因此在学术界，不少科学家能够重写同样功能的工具库，但是很难达到 AT&T 工具库的效率（即运算速度），这的确是一件令人遗憾的事。

数学之美 系列十一 - Google 阿卡 47 的制造者阿米特.辛格博士

枪迷或者看过尼古拉斯.凯奇（Nicolas Cage)主演的电影“战争之王”（Lord of
War)的人也许还记得影片开头的一段话：（在所有轻武器中，）最有名的是阿卡 47( AK47)冲锋枪(也就是中国的五六式冲锋枪的原型），因为它从不卡壳、从不损坏、可在任何环境下使用、可靠性好、杀伤力大并且操作简单。
我认为，在计算机中一个好的算法，应该向阿卡 47 冲锋枪那样简单、有效、可靠性好而且容易读懂(或者说易操作），而不应该是故弄玄虚。Google 的杰出工程师阿米特.辛格博士 (Amit Singhal) 就是为 Google 设计阿卡 47 冲锋枪的人，在公司内部，Google 的排序算法便是以他的名字命名的。
从加入 Google 的第一天，我就开始了和辛格长期而愉快的合作，而他一直是我的一个良师益友。辛格、Matt Cutts（中国一些用户误认为他是联邦调查局特工，当然他不是）、马丁和我四个人当时一同研究和解决网络搜索中的作弊问题（Spam)。我们需要建一个分类器，我以前一直在学术界工作和学习，比较倾向找一个很漂亮的解决方案。我设计了一个很完美的分类器，大约要花三个月到半年时间来实现和训练，而辛格认为找个简单有效的办法就行了。我们于是尽可能简化问题，一、两个月就把作弊的数量减少了一半。当时我们和公司工程副总裁罗森打了个赌，如果我们能减少 40% 的作弊，他就送我们四个家庭去夏威夷度假，后来罗森真的履约了。这个分类器设计得非常小巧（只用很小的内存），而且非常快速（几台服务器就能处理全球搜索的分类），至今运行得很好。
后来我和辛格一起又完成了许多项目，包括对中、日、韩文排名算法的改进。每一次，辛格总是坚持找简单有效的解决方案。这种做法在 Google 这个人才济济的公司常常招人反对，因为很多资深的工程师怀疑这些简单方法的有效性。不少人试图用精确而复杂的办法对辛格的设计的各种“阿卡47” 进行改进，后来发现几乎所有时候，辛格的简单方法都接近最优化的解决方案，而且还快得多。另一条选择简单方案的原因是这样设计的系统很容易查错（debug)。
当然，辛格之所以总是能找到那些简单有效的方法，不是靠直觉，更不是撞大运，而是靠他丰富的研究经验。辛格早年从师于搜索大师萨尔顿(Salton)教授，毕业后就职于 AT&T 实验室。在那里，他和两个同事半年就搭起了一个中等规模的搜索引擎，这个引擎索引的网页数量虽然无法和商用的引擎相比，但是准确性却非常好。在 AT&T，他对搜索问题的各个细节进行了仔细的研究，他的那些简单而有效的解决方案，常常是深思熟虑去伪存真的结果。
辛格非常鼓励年轻人不怕失败，大胆尝试。一次一位刚毕业不久的工程师因为把带有错误的程序推出到 Google 的服务器上而惶惶不可终日。辛格安慰她讲，你知道，我在 Google 犯的最大一次错误是曾经将所有网页的相关性得分全部变成了零，于是所有搜索的结果全部是随机的了。这位工程师后来为 Google 开发了很多好的产品。
辛格在 AT&T 时确立了他在学术界的地位，但是，他不是一个满足于做实验写论文的人，于是他离开了实验室来到了当时只有百、十人的 Google。在这里，他得以施展才智，重写了 Google 的排名算法，并且一直在负责改进它。辛格因为舍不得放下两个孩子，很少参加各种会议，但是他仍然被学术界公认为是当今最权威的网络搜索专家。2005年，辛格作为杰出校友被请回母校康乃尔大学计算机系在 40 年系庆上作报告，获得这一殊荣的还有大名鼎鼎的美国工程院院士，计算机独立磁盘冗余阵列（RAID)的发明人凯茨(Randy Katz) 教授。

数学之美 系列 12 - 余弦定理和新闻的分类

余弦定理和新闻的分类似乎是两件八杆子打不着的事，但是它们确有紧密的联系。具体说，新闻的分类很大程度上依靠余弦定理。
Google 的新闻是自动分类和整理的。所谓新闻的分类无非是要把相似的新闻放到一类中。计算机其实读不懂新闻，它只能快速计算。这就要求我们设计一个算法来算出任意两篇新闻的相似性。为了做到这一点，我们需要想办法用一组数字来描述一篇新闻。
我们来看看怎样找一组数字，或者说一个向量来描述一篇新闻。回忆一下我们在“如何度量网页相关性”一文中介绍的TF/IDF 的概念。对于一篇新闻中的所有实词，我们可以计算出它们的单文本词汇频率/逆文本频率值（TF/IDF)。不难想象，和新闻主题有关的那些实词频率高，TF/IDF 值很大。我们按照这些实词在词汇表的位置对它们的 TF/IDF 值排序。比如，词汇表有六万四千个词，分别为
单词编号 汉字词
------------------
1 阿
2 啊
3 阿斗
4 阿姨
...
789 服装
....
64000 做作
在一篇新闻中，这 64,000 个词的 TF/IDF 值分别为
单词编号 TF/IDF 值
==============
1 0
2 0.0034
3 0
4 0.00052
5 0
...
789 0.034
...
64000 0.075
如果单词表中的某个次在新闻中没有出现，对应的值为零，那么这 64,000 个数，组成一个64,000维的向量。我们就用这个向量来代表这篇新闻，并成为新闻的特征向量。如果两篇新闻的特征向量相近，则对应的新闻内容相似，它们应当归在一类，反之亦然。
学过向量代数的人都知道，向量实际上是多维空间中有方向的线段。如果两个向量的方向一致，即夹角接近零，那么这两个向量就相近。而要确定两个向量方向是否一致，这就要用到余弦定理计算向量的夹角了。
余弦定理对我们每个人都不陌生，它描述了三角形中任何一个夹角和三个边的关系，换句话说，给定三角形的三条边，我们可以用余弦定理求出三角形各个角的角度。假定三角形的三条边为 a, b 和 c，对应的三个角为 A, B 和 C，那么角 A 的余弦 --

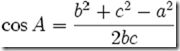
如果我们将三角形的两边 b 和 c 看成是两个向量，那么上述公式等价于

其中分母表示两个向量 b 和 c 的长度，分子表示两个向量的内积。举一个具体的例子，假如新闻 X 和新闻 Y 对应向量分别是
x1,x2,...,x64000 和
y1,y2,...,y64000,
那么它们夹角的余弦等于，

当两条新闻向量夹角的余弦等于一时，这两条新闻完全重复（用这个办法可以删除重复的网页）；当夹角的余弦接近于一时，两条新闻相似，从而可以归成一类；夹角的余弦越小，两条新闻越不相关。

我们在中学学习余弦定理时，恐怕很难想象它可以用来对新闻进行分类。在这里，我们再一次看到数学工具的用途。

数学之美 系列十三 信息指纹及其应用

任何一段信息文字，都可以对应一个不太长的随机数，作为区别它和其它信息的指纹（Fingerprint)。只要算法设计的好，任何两段信息的指纹都很难重复，就如同人类的指纹一样。信息指纹在加密、信息压缩和处理中有着广泛的应用。
我们在图论和网络爬虫一文中提到，为了防止重复下载同一个网页，我们需要在哈希表中纪录已经访问过的网址（URL)。但是在哈希表中以字符串的形式直接存储网址，既费内存空间，又浪费查找时间。现在的网址一般都较长，比如，如果在 Google 或者百度在查找数学之美，对应的网址长度在一百个字符以上。下面是百度的链接

http://www.baidu.com/s?ie=gb2312&bs=%CA%FD%D1%A7%D6%AE%C3%C0&sr=&z=&cl=3&f=8
&wd=%CE%E2%BE%FC+%CA%FD%D1%A7%D6%AE%C3%C0&ct=0
假定网址的平均长度为一百个字符，那么存贮 200 亿个网址本身至少需要 2 TB，即两千 GB 的容量，考虑到哈希表的存储效率一般只有 50%，实际需要的内存在 4 TB以上。即使把这些网址放到了计算机的内存中，由于网址长度不固定，以字符串的形式查找的效率会很低。因此，我们如果能够找到一个函数，将这 200 亿个网址随机地映射到128 二进位即 16 个字节的整数空间，比如将上面那个很长的字符串对应成一个如下的随机数:
893249432984398432980545454543
这样每个网址只需要占用 16 个字节而不是原来的一百个。这就能把存储网址的内存需求量降低到原来的 1/6。这个16 个字节的随机数，就称做该网址的信息指纹（Fingerprint)。可以证明，只要产生随机数的算法足够好，可以保证几乎不可能有两个字符串的指纹相同，就如同不可能有两个人的指纹相同一样。由于指纹是固定的 128 位整数，因此查找的计算量比字符串比较小得多。网络爬虫在下载网页时，它将访问过的网页的网址都变成一个个信息指纹，存到哈希表中，每当遇到一个新网址时，计算机就计算出它的指纹，然后比较该指纹是否已经在哈希表中，来决定是否下载这个网页。这种整数的查找比原来字符串查找,可以快几倍到几十倍。
产生信息指纹的关键算法是伪随机数产生器算法（prng)。最早的 prng 算法是由计算机之父冯诺伊曼提出来的。他的办法非常简单，就是将一个数的平方掐头去尾，取中间的几位数。比如一个四位的二进制数 1001（相当于十进制的9），其平方为 01010001 (十进制的 81）掐头去尾剩下中间的四位 0100。当然这种方法产生的数字并不很随机，也就是说两个不同信息很有可能有同一指纹。现在常用的 MersenneTwister 算法要好得多。
信息指纹的用途远不止网址的消重，信息指纹的的孪生兄弟是密码。信息指纹的一个特征是其不可逆性, 也就是说,
无法根据信息指纹推出原有信息，这种性质， 正是网络加密传输所需要的。比如说，一个网站可以根据用户的Cookie 识别不同用户，这个 cookie 就是信息指纹。但是网站无法根据信息指纹了解用户的身份，这样就可以保护用户的隐私。在互联网上，加密的可靠性，取决于是否很难人为地找到拥有同一指纹的信息， 比如一个黑客是否能随意产生用户的 cookie。从加密的角度讲 MersenneTwister，算法并不好，因为它产生的随机数有相关性。
互联网上加密要用基于加密伪随机数产生器（csprng)。常用的算法有 MD5 或者 SHA1 等标准，它们可以将不定长的信息变成定长的 128 二进位或者 160 二进位随机数。值得一提的事，SHA1 以前被认为是没有漏洞的，现在已经被中国的王小云教授证明存在漏洞。但是大家不必恐慌， 因为这和黑客能真正攻破你的注册信息是还两回事。
信息指纹的虽然历史很悠久，但真正的广泛应用是在有了互联网以后，这几年才渐渐热门起来。

数学之美 十四 谈谈数学模型的重要性

[注：一直关注数学之美系列的读者可能已经发现，我们对任何问题总是在找相应的准确的数学模型。为了说明模型的重要性，今年七月份我在 Google 中国内部讲课时用了整整一堂课来讲这个问题，下面的内容是我讲座的摘要。］
在包括哥白尼、伽利略和牛顿在内的所有天文学家中，我最佩服的是地心说的提出者托勒密。虽然天文学起源于古埃及，并且在古巴比伦时，人们就观测到了五大行星（金、木、水、火、土）运行的轨迹，以及行星在近日点运动比远日点快。（下图是在地球上看到的金星的轨迹，看过达芬奇密码的读者知道金星大约每四年在天上画一个五角星。）

但是真正创立了天文学，并且计算出诸多天体运行轨迹的是两千年前古罗马时代的托勒密。虽然今天我们可能会嘲笑托勒密犯的简单的错误，但是真正了解托勒密贡献的人都会对他肃然起敬。托勒密发明了球坐标，定义了包括赤道和零度经线在内的经纬线，他提出了黄道，还发明了弧度制。
当然，他最大也是最有争议的发明是地心说。虽然我们知道地球是围绕太阳运动的，但是在当时，从人们的观测出发，很容易得到地球是宇宙中心的结论。从地球上看，行星的运动轨迹是不规则的，托勒密的伟大之处是用四十个小圆套大圆的方法，精确地计算出了所有行星运动的轨迹。（托勒密继承了毕达格拉斯的一些思想，他也认为圆是最完美的几何图形。）托勒密模型的精度之高，让以后所有的科学家惊叹不已。即使今天，我们在计算机的帮助下，也很难解出四十个套在一起的圆的方程。每每想到这里，我都由衷地佩服托勒密。一千五百年来，人们根据他的计算决定农时。但是，经过了一千五百年，托勒密对太阳运动的累积误差，还是差出了一星期。

地心说的示意图，我国天文学家张衡的浑天地动说其实就是地心说。
纠正地心说错误不是靠在托勒密四十个圆的模型上再多套上几个圆，而是进一步探索真理。哥白尼发现，如果以太阳为中心来描述星体的运行，只需要 8-10 个圆，就能计算出一个行星的运动轨迹，他提出了日心说。很遗憾的事，哥白尼正确的假设并没有得到比托勒密更好的结果，哥白尼的模型的误差比托勒密地要大不少。这是教会和当时人们认为哥白尼的学说是邪说的一个原因，所以日心说要想让人心服口服地接受，就得更准确地描述行星运动。
完成这一使命的是开普勒。开普勒在所有一流的天文学家中，资质较差，一生中犯了无数低级的错误。但是他有两条别人没有的东西，从他的老师第谷手中继承的大量的、在当时最精确的观测数据，以及运气。开普勒很幸运地发现了行星围绕太阳运转的轨道实际是椭圆形的，这样不需要用多个小圆套大圆，而只要用一个椭圆就能将星体运动规律描述清楚了。只是开普勒的知识和水平不足以解释为什么行星的轨道是椭圆形的。最后是伟大的科学家牛顿用万有引力解释了这个问题。
故事到这里似乎可以结束了。但是，许多年后，又有了个小的波澜。天文学家们发现，天王星的实际轨迹和用椭圆模型算出来的不太符合。当然，偷懒的办法是接着用小圆套大圆的方法修正，但是一些严肃的科学家在努力寻找真正的原因。英国的亚当斯和法国的维内尔（Verrier）独立地发现了吸引天王星偏离轨道的海王星。
讲座结束前，我和 Google 中国的工程师们一同总结了这么几个结论：
１.　一个正确的数学模型应当在形式上是简单的。（托勒密的模型显然太复杂。）
２.　一个正确的模型在它开始的时候可能还不如一个精雕细琢过的错误的模型来的准确，但是，如果我们认定大方向是对的，就应该坚持下去。（日心说开始并没有地心说准确。）
３.　大量准确的数据对研发很重要。
４.　正确的模型也可能受噪音干扰，而显得不准确；这时我们不应该用一种凑合的修正方法来弥补它，而是要找到噪音的根源，这也许能通往重大发现。
在网络搜索的研发中，我们在前面提到的单文本词频/逆文本频率指数（TF/IDF) 和网页排名（page rank)都相当于是网络搜索中的“椭圆模型”，它们都很简单易懂。

数学之美 系列十五 繁与简 自然语言处理的几位精英

我在数学之美系列中一直强调的一个好方法就是简单。但是，事实上，自然语言处理中也有一些特例，比如有些学者将一个问题研究到极致，执著追求完善甚至可以说完美的程度。他们的工作对同行有很大的参考价值，因此我们在科研中很需要这样的学者。在自然语言处理方面新一代的顶级人物麦克尔 · 柯林斯 (Michael Collins) 就是这样的人。
柯林斯：追求完美
柯林斯从师于自然语言处理大师马库斯 (Mitch Marcus)（我们以后还会多次提到马库斯），从宾夕法利亚大学获得博士学位，现任麻省理工学院 (MIT) 副教授（别看他是副教授，他的水平在当今自然语言处理领域是数一数二的），在作博士期间，柯林斯写了一个后来以他名字命名的自然语言文法分析器 (sentence parser)，可以将书面语的每一句话准确地进行文法分析。文法分析是很多自然语言应用的基础。虽然柯林斯的师兄布莱尔 (Eric Brill) 和 Ratnaparkhi 以及师弟 Eisnar 都完成了相当不错的语言文法分析器，但是柯林斯却将它做到了极致，使它在相当长一段时间内成为世界上最好的文法分析器。柯林斯成功的关键在于将文法分析的每一个细节都研究得很仔细。柯林斯用的数学模型也很漂亮，整个工作可以用完美来形容。我曾因为研究的需要，找柯林斯要过他文法分析器的源程序，他很爽快地给了我。我试图将他的程序修改一下来满足我特定应用的要求，但后来发现，他的程序细节太多以至于很难进一步优化。柯林斯的博士论文堪称是自然语言处理领域的范文。它像一本优秀的小说，把所有事情的来龙去脉介绍的清清楚楚，对于任何有一点计算机和自然语言处理知识的人，都可以轻而易举地读懂他复杂的方法。
柯林斯毕业后，在 AT&T 实验室度过了三年快乐的时光。在那里柯林斯完成了许多世界一流的研究工作诸如隐含马尔科夫模型的区别性训练方法，卷积核在自然语言处理中的应用等等。三年后，AT&T 停止了自然语言处理方面的研究，柯林斯幸运地在 MIT 找到了教职。在 MIT 的短短几年间，柯林斯多次在国际会议上获得最佳论文奖。相比其他同行，这种成就是独一无二的。柯林斯的特点就是把事情做到极致。如果说有人喜欢“繁琐哲学”，柯林斯就是一个。
布莱尔：简单才美
在研究方法上，站在柯林斯对立面的典型是他的师兄艾里克 · 布莱尔 (Eric Brill) 和雅让斯基，后者我们已经介绍过了，这里就不再重复。与柯林斯从工业界到学术界相反，布莱尔职业路径是从学术界走到工业界。与柯里斯的研究方法相反，布莱尔总是试图寻找简单得不能再简单的方法。布莱尔的成名作是基于变换规则的机器学习方法 (transformation rule based machine learning)。这个方法名称虽然很复杂，其实非常简单。我们以拼音转换字为例来说明它：
第一步，我们把每个拼音对应的汉字中最常见的找出来作为第一遍变换的结果，当然结果有不少错误。比如，“常识”可能被转换成“长识”；
第二步，可以说是“去伪存真”，我们用计算机根据上下文，列举所有的同音字替换的规则，比如，如果 chang 被标识成“长”，但是后面的汉字是“识”，则将“长”改成“常”；
第三步，应该就是“去粗取精”，将所有的规则用到事先标识好的语料中，挑出有用的，删掉无用的。然后重复二三步，直到找不到有用的为止。
布莱尔就靠这么简单的方法，在很多自然语言研究领域，得到了几乎最好的结果。由于他的方法再简单不过了，许许多多的人都跟着学。布莱尔可以算是我在美国的第一个业师，我们俩就用这么简单的方法作词性标注 (part of speech tagging)，也就是把句子中的词标成名词动词，很多年内无人能超越。（最后超越我们的是后来加入 Google 的一名荷兰工程师，用的是同样的方法，但是做得细致很多）布莱尔离开学术界后去了微软研究院。在那里的第一年，他一人一年完成的工作比组里其他所有人许多年做的工作的总和还多。后来，布莱尔又加入了一个新的组，依然是高产科学家。据说，他的工作真正被微软重视要感谢 Google，因为有了 Google，微软才对他从人力物力上给于了巨大的支持，使得布莱尔成为微软搜索研究的领军人物之一。在研究方面，布莱尔有时不一定能马上找到应该怎么做，但是能马上否定掉一种不可能的方案。这和他追求简单的研究方法有关，他能在短时间内大致摸清每种方法的好坏。
由于布莱尔总是找简单有效的方法，而又从不隐瞒自己的方法，所以他总是很容易被包括作者我自己在内的很多人赶上和超过。好在布莱尔很喜欢别人追赶他，因为，当人们在一个研究方向超过他时，他已经调转船头驶向它方了。一次，艾里克对我说，有一件事我永远追不上他，那就是他比我先有了第二个孩子 ：）
在接下来了系列里，我们还会介绍一个繁与简结合的例子。

数学之美 系列十六 （下）－ 不要把所有的鸡蛋放在一个篮子里　最大熵模型

我们上次谈到用最大熵模型可以将各种信息综合在一起。我们留下一个问题没有回答，就是如何构造最大熵模型。我们已经所有的最大熵模型都是指数函数的形式，现在只需要确定指数函数的参数就可以了，这个过程称为模型的训练。
最原始的最大熵模型的训练方法是一种称为通用迭代算法 GIS(generalized iterative scaling) 的迭代 算法。GIS 的原理并不复杂，大致可以概括为以下几个步骤：
1. 假定第零次迭代的初始模型为等概率的均匀分布。
2. 用第 N 次迭代的模型来估算每种信息特征在训练数据中的分布，如果超过了实际的，就把相应的模型参数变小；否则，将它们便大。
3. 重复步骤 2 直到收敛。
GIS 最早是由 Darroch 和 Ratcliff 在七十年代提出的。但是，这两人没有能对这种算法的物理含义进行很好地解释。后来是由数学家希萨（Csiszar)解释清楚的，因此，人们在谈到这个算法时，总是同时引用 Darroch 和Ratcliff 以及希萨的两篇论文。GIS 算法每次迭代的时间都很长，需要迭代很多次才能收敛，而且不太稳定，即使在 64 位计算机上都会出现溢出。因此，在实际应用中很少有人真正使用 GIS。大家只是通过它来了解最大熵模型的算法。
八十年代，很有天才的孪生兄弟的达拉皮垂(Della Pietra)在 IBM 对 GIS 算法进行了两方面的改进，提出了改进迭代算法 IIS（improved iterative scaling）。这使得最大熵模型的训练时间缩短了一到两个数量级。这样最大熵模型才有可能变得实用。即使如此，在当时也只有 IBM 有条件是用最大熵模型。
由于最大熵模型在数学上十分完美，对科学家们有很大的诱惑力，因此不少研究者试图把自己的问题用一个类似最大熵的近似模型去套。谁知这一近似，最大熵模型就变得不完美了，结果可想而知，比打补丁的凑合的方法也好不了多少。于是，不少热心人又放弃了这种方法。第一个在实际信息处理应用中验证了最大熵模型的优势的，是宾夕法尼亚大学马库斯的另一个高徒原 IBM 现微软的研究员拉纳帕提(Adwait Ratnaparkhi)。拉纳帕提的聪明之处在于他没有对最大熵模型进行近似，而是找到了几个最适合用最大熵模型、而计算量相对不太大的自然语言处理问题，比如词性标注和句法分析。拉纳帕提成功地将上下文信息、词性（名词、动词和形容词等）、句子成分（主谓宾）通过最大熵模型结合起来，做出了当时世界上最好的词性标识系统和句法分析器。拉纳帕提的论文发表后让人们耳目一新。拉纳帕提的词性标注系统，至今仍然是使用单一方法最好的系统。科学家们从拉纳帕提的成就中，又看到了用最大熵模型解决复杂的文字信息处理的希望。
但是，最大熵模型的计算量仍然是个拦路虎。我在学校时花了很长时间考虑如何简化最大熵模型的计算量。终于有一天，我对我的导师说，我发现一种数学变换，可以将大部分最大熵模型的训练时间在 IIS 的基础上减少两个数量级。我在黑板上推导了一个多小时，他没有找出我的推导中的任何破绽，接着他又回去想了两天，然后告诉我我的算法是对的。从此，我们就建造了一些很大的最大熵模型。这些模型比修修补补的凑合的方法好不少。即使在我找到了快速训练算法以后，为了训练一个包含上下文信息，主题信息和语法信息的文法模型(language model)，我并行使用了 20 台当时最快的 SUN 工作站，仍然计算了三个月。由此可见最大熵模型的复杂的一面。最大熵模型快速算法的实现很复杂，到今天为止，世界上能有效实现这些算法的人也不到一百人。有兴趣实现一个最大熵模型的读者可以阅读我的论文。
最大熵模型，可以说是集简与繁于一体，形式简单，实现复杂。值得一提的是，在Google的很多产品中，比如机器翻译，都直接或间接地用到了最大熵模型。
讲到这里，读者也许会问，当年最早改进最大熵模型算法的达拉皮垂兄弟这些年难道没有做任何事吗？他们在九十年代初贾里尼克离开 IBM 后，也退出了学术界，而到在金融界大显身手。他们两人和很多 IBM 语音识别的同事一同到了一家当时还不大，但现在是世界上最成功对冲基金(hedge fund)公司----文艺复兴技术公司 (Renaissance Technologies)。我们知道，决定股票涨落的因素可能有几十甚至上百种，而最大熵方法恰恰能找到一个同时满足成千上万种不同条件的模型。达拉皮垂兄弟等科学家在那里，用于最大熵模型和其他一些先进的数学工具对股票预测，获得了巨大的成功。从该基金 1988 年创立至今，它的净回报率高达平均每年 34%。也就是说，如果 1988 年你在该基金投入一块钱，今天你能得到 200 块钱。这个业绩，远远超过股神巴菲特的旗舰公司伯克夏哈撒韦（Berkshire Hathaway)。同期，伯克夏哈撒韦的总回报是 16 倍。
值得一提的是，信息处理的很多数学手段，包括隐含马尔可夫模型、子波变换、贝叶斯网络等等，在华尔街多有直接的应用。由此可见，数学模型的作用。

数学之美 系列十七 闪光的不一定是金子 谈谈搜索引擎作弊问题(Search Engine Anti-SPAM)

自从有了搜索引擎，就有了针对搜索引擎网页排名的作弊(SPAM)。以至于用户发现在搜索引擎中排名靠前的网页不一定就是高质量的，用句俗话说，闪光的不一定是金子。

搜索引擎的作弊，虽然方法很多，目的只有一个，就是采用不正当手段提高自己网页的排名。早期最常见的作弊方法是重复关键词。比如一个卖数码相机的网站，重复地罗列各种数码相机的品牌，如尼康、佳能和柯达等等。为了不让读者看到众多讨厌的关键词，聪明一点的作弊者常用很小的字体和与背景相同的颜色来掩盖这些关键词。其实，这种做法很容易被搜索引擎发现并纠正。
在有了网页排名(page rank)以后，作弊者发现一个网页被引用的连接越多，排名就可能越靠前，于是就有了专门卖链接和买链接的生意。比如，有人自己创建成百上千个网站，这些网站上没有实质的内容，只有到他们的客户网站的连接。这种做法比重复关键词要高明得多，但是还是不太难被发现。因为那些所谓帮别人提高排名的网站，为了维持生意需要大量地卖链接，所以很容易露马脚。（这就如同造假钞票，当某一种假钞票的流通量相当大以后，就容易找到根源了。）再以后，又有了形形色色的作弊方式，我们就不在这里一一赘述了。
几年前，我加入Google做的第一件事就是消除网络作弊。在Google最早发现搜索引擎作弊的是Matt Cutts，他在我加入Google前几个月开始研究这个问题，后来，辛格，马丁和我先后加入进来。我们经过几个月的努力，清除了一半的作弊者。(当然，以后抓作弊的效率就不会有这么高了。）其中一部分网站从此"痛改前非"，但是还是有很多网站换一种作弊方法继续作弊，因此，抓作弊成了一种长期的猫捉老鼠的游戏。虽然至今还没有一个一劳永逸地解决作弊问题的方法，但是，Google基本做到了对于任何已知的作弊方法，在一定时间内发现并清除它，从而总是将作弊的网站的数量控制在一个很小的比例范围。
抓作弊的方法很像信号处理中的去噪音的办法。学过信息论和有信号处理经验的读者可能知道这么一个事实，我们如果在发动机很吵的汽车里用手机打电话，对方可能听不清；但是如果我们知道了汽车发动机的频率，我们可以加上一个和发动机噪音相反的信号，很容易地消除发动机的噪音，这样，收话人可以完全听不到汽车的噪音。事实上，现在一些高端的手机已经有了这种检测和消除噪音的功能。消除噪音的流程可以概括如下：

在图中，原始的信号混入了噪音，在数学上相当于两个信号做卷积。噪音消除的过程是一个解卷积的过程。这在信号处理中并不是什么难题。因为第一，汽车发动机的频率是固定的，第二，这个频率的噪音重复出现，只要采集几秒钟的信号进行处理就能做到。从广义上讲，只要噪音不是完全随机的、并且前后有相关性，就可以检测到并且消除。（事实上，完全随机不相关的高斯白噪音是很难消除的。）
搜索引擎的作弊者所作的事，就如同在手机信号中加入了噪音，使得搜索结果的排名完全乱了。但是，这种人为加入的噪音并不难消除，因为作弊者的方法不可能是随机的（否则就无法提高排名了）。而且，作弊者也不可能是一天换一种方法，即作弊方法是时间相关的。因此，搞搜索引擎排名算法的人，可以在搜集一段时间的作弊信息后，将作弊者抓出来，还原原有的排名。当然这个过程需要时间，就如同采集汽车发动机噪音需要时间一样，在这段时间内，作弊者可能会尝到些甜头。因此，有些人看到自己的网站经过所谓的优化（其实是作弊），排名在短期内靠前了，以为这种所谓的优化是有效的。但是，不久就会发现排名掉下去了很多。这倒不是搜索引擎以前宽容，现在严厉了，而是说明抓作弊需要一定的时间，以前只是还没有检测到这些作弊的网站而已。
还要强调一点，Google抓作弊和恢复网站原有排名的过程完全是自动的(并没有个人的好恶），就如同手机消除噪音是自动的一样。一个网站要想长期排名靠前，就需要把内容做好，同时要和那些作弊网站划清界限。

数学之美 系列十八 － 矩阵运算和文本处理中的分类问题

我在大学学习线性代数时，实在想不出它除了告诉我们如何解线性方程外，还能有什么别的用途。关于矩阵的许多概念，比如特征值等等，更是脱离日常生活。后来在数值分析中又学了很多矩阵的近似算法，还是看不到可以应用的地方。当时选这些课，完全是为了混学分的学位。我想，很多同学都多多少少有过类似的经历。直到后来长期做自然语言处理的研究，我才发现数学家们提出那些矩阵的概念和算法，是有实际应用的意义的。
在自然语言处理中，最常见的两类的分类问题分别是，将文本按主题归类（比如将所有介绍亚运会的新闻归到体育类）和将词汇表中的字词按意思归类（比如将各种体育运动的名称个归成一类）。这两种分类问题都可用通过矩阵运算来圆满地、同时解决。为了说明如何用矩阵这个工具类解决这两个问题的，让我们先来来回顾一下我们在余弦定理和新闻分类中介绍的方法。
分类的关键是计算相关性。我们首先对两个文本计算出它们的内容词，或者说实词的向量，然后求这两个向量的夹角。当这两个向量夹角为零时，新闻就相关；当它们垂直或者说正交时，新闻则无关。当然，夹角的余弦等同于向量的内积。从理论上讲，这种算法非常好。但是计算时间特别长。通常，我们要处理的文章的数量都很大，至少在百万篇以上，二次回标有非常长，比如说有五十万个词（包括人名地名产品名称等等）。如果想通过对一百万篇文章两篇两篇地成对比较，来找出所有共同主题的文章，就要比较五千亿对文章。现在的计算机一秒钟最多可以比较一千对文章，完成这一百万篇文章相关性比较就需要十五年时间。注意，要真正完成文章的分类还要反复重复上述计算。
在文本分类中，另一种办法是利用矩阵运算中的奇异值分解（Singular Value Decomposition，简称 SVD)。现在让我们来看看奇异值分解是怎么回事。首先，我们可以用一个大矩阵A来描述这一百万篇文章和五十万词的关联性。这个矩阵中，每一行对应一篇文章，每一列对应一个词。

在上面的图中，M=1,000,000，N=500,000。第 i 行，第 j 列的元素，是字典中第 j 个词在第 i 篇文章中出现的加权词频（比如，TF/IDF)。读者可能已经注意到了，这个矩阵非常大，有一百万乘以五十万，即五千亿个元素。
奇异值分解就是把上面这样一个大矩阵，分解成三个小矩阵相乘，如下图所示。比如把上面的例子中的矩阵分解成一个一百万乘以一百的矩阵X，一个一百乘以一百的矩阵B，和一个一百乘以五十万的矩阵Y。这三个矩阵的元素总数加起来也不过1.5亿，仅仅是原来的三千分之一。相应的存储量和计算量都会小三个数量级以上。

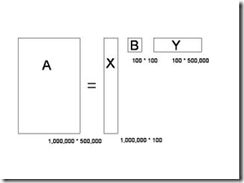
三个矩阵有非常清楚的物理含义。第一个矩阵X中的每一行表示意思相关的一类词，其中的每个非零元素表示这类词中每个词的重要性（或者说相关性），数值越大越相关。最后一个矩阵Y中的每一列表示同一主题一类文章，其中每个元素表示这类文章中每篇文章的相关性。中间的矩阵则表示类词和文章雷之间的相关性。因此，我们只要对关联矩阵A进行一次奇异值分解，w 我们就可以同时完成了近义词分类和文章的分类。（同时得到每类文章和每类词的相关性）。
现在剩下的唯一问题，就是如何用计算机进行奇异值分解。这时，线性代数中的许多概念，比如矩阵的特征值等等，以及数值分析的各种算法就统统用上了。在很长时间内，奇异值分解都无法并行处理。（虽然 Google 早就有了MapReduce 等并行计算的工具，但是由于奇异值分解很难拆成不相关子运算，即使在 Google 内部以前也无法利用并行计算的优势来分解矩阵。）最近，Google 中国的张智威博士和几个中国的工程师及实习生已经实现了奇异值分解的并行算法，我认为这是 Google 中国对世界的一个贡献。

数学之美 系列十九 － 马尔可夫链的扩展 贝叶斯网络 (Bayesian Networks)

我们在前面的系列中多次提到马尔可夫链 (Markov
Chain)，它描述了一种状态序列，其每个状态值取决于前面有限个状态。这种模型，对很多实际问题来讲是一种很粗略的简化。在现实生活中，很多事物相互的关系并不能用一条链来串起来。它们之间的关系可能是交叉的、错综复杂的。比如在下图中可以看到，心血管疾病和它的成因之间的关系是错综复杂的。显然无法用一个链来表示。

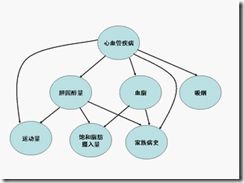
我们可以把上述的有向图看成一个网络，它就是贝叶斯网络。其中每个圆圈表示一个状态。状态之间的连线表示它们的因果关系。比如从心血管疾病出发到吸烟的弧线表示心血管疾病可能和吸烟有关。当然，这些关系可以有一个量化的可信度 (belief)，用一个概率描述。我们可以通过这样一张网络估计出一个人的心血管疾病的可能性。在网络中每个节点概率的计算，可以用贝叶斯公式来进行，贝叶斯网络因此而得名。由于网络的每个弧有一个可信度，贝叶斯网络也被称作信念网络 (belief networks)。
和马尔可夫链类似，贝叶斯网络中的每个状态值取决于前面有限个状态。不同的是，贝叶斯网络比马尔可夫链灵活，它不受马尔可夫链的链状结构的约束，因此可以更准确地描述事件之间的相关性。可以讲，马尔可夫链是贝叶斯网络的特例，而贝叶斯网络是马尔可夫链的推广。
使用贝叶斯网络必须知道各个状态之间相关的概率。得到这些参数的过程叫做训练。和训练马尔可夫模型一样，训练贝叶斯网络要用一些已知的数据。比如在训练上面的网络，需要知道一些心血管疾病和吸烟、家族病史等有关的情况。相比马尔可夫链，贝叶斯网络的训练比较复杂，从理论上讲，它是一个 NP-complete 问题，也就是说，对于现在的计算机是不可计算的。但是，对于某些应用，这个训练过程可以简化，并在计算上实现。
值得一提的是 IBM Watson 研究所的茨威格博士 (Geoffrey Zweig) 和西雅图华盛顿大学的比尔默 (Jeff Bilmes) 教授完成了一个通用的贝叶斯网络的工具包，提供给对贝叶斯网络有兴趣的研究者。
贝叶斯网络在图像处理、文字处理、支持决策等方面有很多应用。在文字处理方面，语义相近的词之间的关系可以用一个贝叶斯网络来描述。我们利用贝叶斯网络，可以找出近义词和相关的词，在 Google 搜索和 Google 广告中都有直接的应用。

数学之美 系列二十 －自然语言处理的教父 马库斯

我们在前面的系列中介绍和提到了一些年轻有为的科学家，迈克尔·柯林斯，艾里克·布莱尔，大卫·雅让斯基，拉纳帕提等等，他们都出自宾夕法尼亚计算机系米奇·马库斯(Mitch Marcus)名下。就像许多武侠小说中描写的，弟子都成了各派的掌门，师傅一定了不得。的确，马库斯虽然作为第一作者发表的论文并不多，但是从很多角度上讲，他可以说是自然语言处理领域的教父。
马库斯教授长期当任宾夕法尼亚大学计算机系主任，直到他在几年前从 AT&T 找到皮耶尔替代他为止。作为一个管理者，马库斯显示出在自然处理和计算机科学方面的卓识的远见。在指导博士生时，马库斯发现语料库在自然语言处理中的重要性。马库斯呕心沥血，花了十几年工夫建立了一系列标准的语料库，提供给全世界的学者使用。这套被称为 LDC 的语料库，是当今全世界自然语言处理的所有学者都使用的工具。我们在以前的系列中讲到，当今的自然语言处理几乎都是使用给予统计的方法。要做统计，就需要大量有代表性的数据。利用这些数据开发一个自然语言处理系统的过程，可以统称为训练。比如，我们要训练一个汉语分词系统，我们需要一些已经分好词的中文句子。当然这些句子需要有代表性。如果想知道一个分词系统的准确性，我们也需要一些人工分好词的句子进行测试。这些人工处理好的文字数据库，成为语料库(corpus)。如果每个研究室都人工建立几个语料库，不仅浪费时间精力，而且发表文章时，数据没有可比性。因此，马库斯想到了建立一系列标准的语料库为全世界的学者用。他利用自己的影响力让美国自然科学基金会和 DARPA 出钱立项，联络的多所大学和研究机构，建立的数百个标准的语料库。其中最著名的是 PennTree
Bank 的语料库。PennTree Bank 覆盖多种语言（包括中文）。每一种语言，它有几十万到几百万字的有代表性的句子，每个句子都有的词性标注，语法分析树等等。LDC 语料库如今已成为全世界自然语言处理科学家共用的数据库。如今，在自然语言处理方面发表论文，几乎都要提供基于 LDC 语料库的测试结果。
马库斯给予他的博士生研究自己感兴趣的课题的自由，这是他之所以桃李满天下的原因。马库斯对几乎所有的自然语言处理领域有独到的见解。和许多教授让博士生去做他拿到基金的项目，马库斯让博士生提出自己有兴趣的课题，或者用他已有的经费支持学生，或者为他们的项目区申请经费。马库斯高屋建瓴，能够很快的判断一个研究方向是否正确，省去了博士生很多 try-and-error 的时间。因此他的学生有些很快地拿到的博士学位。
作为系主任，马库斯在专业设置方面显示出卓识的远见。我有幸和他在同一个校务顾问委员会任职，一起讨论计算机系的研究方向。马库斯在几年前互联网很热门、很多大学开始互联网研究时，看到 bioinformatics (生物信息学）的重要性，在宾夕法利亚大学设置这个专业，并且在其他大学还没有意识到时，开始招聘这方面的教授。马库斯还建议一些相关领域的教授，包括后来的系主任皮耶尔把一部分精力转到生物信息学方面。马库斯同时向他担任顾问的其他一些大学提出同样的建议。等到网络泡沫破裂以后，很多大学的计算机系开始向生物信息学转向，但是发现已经很难找到这些方面好的教授了。我觉得，当今中国的大学，最需要的就是马库斯这样卓有远见的管理者。
过几天我又要和马库斯一起开顾问委员会的会议了，不知道这次他对计算机科学的发展有什么见解。

数学之美系列二十一 － 布隆过滤器（Bloom Filter）

在日常生活中，包括在设计计算机软件时，我们经常要判断一个元素是否在一个集合中。比如在字处理软件中，需要检查一个英语单词是否拼写正确（也就是要判断它是否在已知的字典中）；在 FBI，一个嫌疑人的名字是否已经在嫌疑名单上；在网络爬虫里，一个网址是否被访问过等等。最直接的方法就是将集合中全部的元素存在计算机中，遇到一个新元素时，将它和集合中的元素直接比较即可。一般来讲，计算机中的集合是用哈希表（hash table）来存储的。它的好处是快速准确，缺点是费存储空间。当集合比较小时，这个问题不显著，但是当集合巨大时，哈希表存储效率低的问题就显现出来了。比如说，一个象 Yahoo,Hotmail 和 Gmai 那样的公众电子邮件（email）提供商，总是需要过滤来自发送垃圾邮件的人（spamer）的垃圾邮件。一个办法就是记录下那些发垃圾邮件的 email 地址。由于那些发送者不停地在注册新的地址，全世界少说也有几十亿个发垃圾邮件的地址，将他们都存起来则需要大量的网络服务器。如果用哈希表，每存储一亿个 email 地址， 就需要 1.6GB 的内存（用哈希表实现的具体办法是将每一个 email 地址对应成一个八字节的信息指纹googlechinablog.com/2006/08/blog-post.html，然后将这些信息指纹存入哈希表，由于哈希表的存储效率一般只有 50%，因此一个 email 地址需要占用十六个字节。一亿个地址大约要 1.6GB， 即十六亿字节的内存）。因此存贮几十亿个邮件地址可能需要上百 GB 的内存。除非是超级计算机，一般服务器是无法存储的。
今天，我们介绍一种称作布隆过滤器的数学工具，它只需要哈希表 1/8 到 1/4 的大小就能解决同样的问题。
布隆过滤器是由巴顿.布隆于一九七零年提出的。它实际上是一个很长的二进制向量和一系列随机映射函数。我们通过上面的例子来说明起工作原理。
假定我们存储一亿个电子邮件地址，我们先建立一个十六亿二进制（比特），即两亿字节的向量，然后将这十六亿个二进制全部设置为零。对于每一个电子邮件地址 X，我们用八个不同的随机数产生器（F1,F2, ...,F8） 产生八个信息指纹（f1, f2, ..., f8）。再用一个随机数产生器 G 把这八个信息指纹映射到 1 到十六亿中的八个自然数 g1, g2, ...,g8。现在我们把这八个位置的二进制全部设置为一。当我们对这一亿个 email 地址都进行这样的处理后。一个针对这些 email 地址的布隆过滤器就建成了。（见下图）

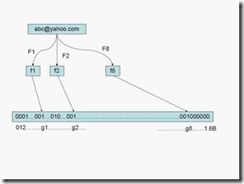
现在，让我们看看如何用布隆过滤器来检测一个可疑的电子邮件地址 Y 是否在黑名单中。我们用相同的八个随机数产生器（F1, F2, ..., F8）对这个地址产生八个信息指纹 s1,s2,...,s8，然后将这八个指纹对应到布隆过滤器的八个二进制位，分别是 t1,t2,...,t8。如果 Y 在黑名单中，显然，t1,t2,..,t8 对应的八个二进制一定是一。这样在遇到任何在黑名单中的电子邮件地址，我们都能准确地发现。
布隆过滤器决不会漏掉任何一个在黑名单中的可疑地址。但是，它有一条不足之处。也就是它有极小的可能将一个不在黑名单中的电子邮件地址判定为在黑名单中，因为有可能某个好的邮件地址正巧对应个八个都被设置成一的二进制位。好在这种可能性很小。我们把它称为误识概率。在上面的例子中，误识概率在万分之一以下。
布隆过滤器的好处在于快速，省空间。但是有一定的误识别率。常见的补救办法是在建立一个小的白名单，存储那些可能别误判的邮件地址。

数学之美系列二十二：由电视剧《暗算》所想到的 — 谈谈密码学的数学原理

前一阵子看了电视剧《暗算》，蛮喜欢它的构思和里面的表演。其中有一个故事提到了密码学，故事本身不错，但是有点故弄玄虚。不过有一点是对的，就是当今的密码学是以数学为基础的。（没有看过暗算的读者可以看一下介绍，http://ent.sina.com.cn/v/2005-10-17/ba866985.shtml
因为我们后面要多次提到这部电视剧。）

密码学的历史大致可以推早到两千年前，相传名将凯撒为了防止敌方截获情报，用密码传送情报。凯撒的做法很简单，就是对二十几个罗马字母建立一张对应表，比如说
    


这样，如果不知道密码本，即使截获一段信息也看不懂，比如收到一个的消息是 EBKTBP，那么在敌人看来是毫无意义的字，通过密码本解破出来就是 CAESAR 一词，即凯撒的名字。这种编码方法史称凯撒大帝。当然，学过信息论的人都知道，只要多截获一些情报，统计一下字母的频率，就可以解破出这种密码。柯蓝道尔在他的“福尔摩斯探案集”中“跳舞的小人”的故事里已经介绍了这种小技巧。在很长时间里，人们试图找到一些好的编码方法使得解密者无法从密码中统计出明码的统计信息，但是，基本上靠经验。有经验的编码者会把常用的词对应成多个密码， 使得破译者很难统计出任何规律。比如，如果将汉语中的“是”一词对应于唯一一个编码 0543，那么破译者就会发现 0543 出现的特别多。但如果将它对应成十个密码 0543，3737，2947 等等，每次随机的挑一个使用，每个密码出现的次数就不会太多，而且破译者也无从知道这些密码其实对应一个字。这里面虽然包含着朴素的概率论的原理，但是并不科学化。另外，好的密码必须做到不能根据已知的明文和密文的对应推断出新的密文的内容。历史上有很多在这方面设计得不周到的密码的例子。在第二次世界大战中，日本军方的密码设计就很成问题。美军破获了日本很多密码。在中途岛海战前，美军截获的日军密电经常出现 AF 这样一个地名，应该是太平洋的某个岛屿，但是美军无从知道是哪个。于是，美军就逐个发表自己控制的每个岛屿上的假新闻。当美军发出“中途岛供水系统坏了”这条假新闻后，从截获的日军情报中又看到 AF 供水出来问题的电文，美军就断定中途岛就是 AF。事实证明判断正确，美军在那里成功地伏击了日本主力舰队。

事实上，在第二次世界大战中，很多顶尖的科学家包括提出信息论的香农都在为美军情报部门工作，而信息论实际上就是情报学的直接产物。香农提出信息论后，为密码学的发展带来了新气象。根据信息论，密码的最高境界是使得敌人在截获密码后，对我方的所知没有任何增加，用信息论的专业术语讲，就是信息量没有增加。一般来讲，当密码之间分布均匀并且统计独立时，提供的信息最少。均匀分布使得敌人无从统计，而统计独立能保证敌人即使看到一段密码和明码后，不能破译另一段密码。这也是《暗算》里传统的破译员老陈破译的一份密报后，但无法推广的原因，而数学家黄依依预见到了这个结果，因为她知道敌人新的密码系统编出的密文是统计独立的。有了信息论后，密码的设计就有了理论基础，现在通用的公开密钥的方法，包括《暗算》里的“光复一号”密码，就是基于这个理论。

公开密钥的原理其实很简单，我们以给上面的单词 Caesar 加解密来说明它的原理。我们先把它变成一组数，比如它的 Ascii 代码 X=099097101115097114（每三位代表一个字母）做明码。现在我们来设计一个密码系统，对这个明码加密。

1，找两个很大的素数（质数）P 和 Q，越大越好，比如 100 位长的, 然后计算它们的乘积 N=P×Q，M=（P-1）×（Q-1）。

2，找一个和 M 互素的整数 E，也就是说 M 和 E 除了 1 以外没有公约数。

3，找一个整数 D，使得 E×D 除以 M 余 1，即 E×D mod M = 1。

现在，世界上先进的、最常用的密码系统就设计好了，其中 E 是公钥谁都可以用来加密，D 是私钥用于解密，一定要自己保存好。乘积 N 是公开的，即使敌人知道了也没关系。

现在，我们用下面的公式对 X 加密，得到密码 Y。
    


好了，现在没有密钥 D，神仙也无法从 Y 中恢复 X。如果知道 D，根据费尔马小定理，则只要按下面的公式就可以轻而易举地从 Y 中得到 X。
    


这个过程大致可以概况如下：
    


公开密钥的好处有：

1.简单。

2.可靠。公开密钥方法保证产生的密文是统计独立而分布均匀的。也就是说，不论给出多少份明文和对应的密文，也无法根据已知的明文和密文的对应来破译下一份密文。更重要的是 N,E 可以公开给任何人加密用，但是只有掌握密钥 D 的人才可以解密, 即使加密者自己也是无法解密的。这样，即使加密者被抓住叛变了，整套密码系统仍然是安全的。（而凯撒大帝的加密方法有一个知道密码本的人泄密，整个密码系统就公开了。）

3.灵活，可以产生很多的公开密钥E和私钥D的组合给不同的加密者。

最后让我们看看破解这种密码的难度。首先，要声明，世界上没有永远破不了的密码，关键是它能有多长时间的有效期。要破公开密钥的加密方式，至今的研究结果表明最好的办法还是对大字 N 进行因数分解，即通过 N 反过来找到 P 和 Q，这样密码就被破了。而找 P 和 Q 目前只有用计算机把所有的数字试一遍这种笨办法。这实际上是在拼计算机的速度，这也就是为什么 P 和 Q 都需要非常大。一种加密方法只有保证 50 年计算机破不了也就可以满意了。前几年破解的 RSA-158 密码是这样因数分解的

395058745832651445264197678006144819960207764603049364541393760515793556265294
50683609727842468219535093544305870490251995655335710209799226484977949442955603
= 3388495837466721394368393204672181522815830368604993048084925840555281177 ×11658823406671259903148376558383270818131012258146392600439520994131344334162924536139

现在，让我们回到《暗算》中，黄依依第一次找的结果经过一系列计算发现无法归零，也就是说除不尽，我猜她可能试图将一个大数 N 做分解，没成功。第二次计算的结果是归零了，说明她找到的 N=P×Q 的分解方法。当然，这件事能不能用算盘完成，我就不知道了，但我觉得比较夸张。另外我对该电视剧还有一个搞不懂的问题就是里面提到的“光复一号”密码的误差问题。一个密码是不能有误差的，否则就是有的密钥也无法解码了。我想可能是指在构造密码时，P 和 Q 之一没找对，其中一个（甚至两个都）不小心找成了合数，这时密码的保密性就差了很多。如果谁知道电视剧里面讲的“误差”是指什么请告诉我。另外，电视剧里提到冯∙诺依曼，说他是现代密码学的祖宗，我想是弄错了，应该是香农。冯∙诺依曼的贡献在发明计算机和提出博弈论（game theory）。

不管怎么样，我们今天用的所谓最可靠的加密方法的数学原理其实就这么简单，一点也不神秘，无非是找几个大素数做一些乘除和乘方运算就可以了。

数学之美系列 二十三 输入一个汉字需要敲多少个键 — 谈谈香农第一定律

今天各种汉字输入法已经很成熟了，随便挑出一种主要的输入法比十几年前最好的输入法都要快、要准。现在抛开具体的输入法，从理论上分析一下，输入汉字到底能有多快。

我们假定常用的汉字在二级国标里面，一共有 6700 个作用的汉字。如果不考虑汉字频率的分布，用键盘上的 26 个字母对汉字编码，两个字母的组合只能对 676 个汉字编码，对 6700 个汉字编码需要用三个字母的组合，即编码长度为三。当然，聪明的读者马上发现了我们可以对常见的字用较短的编码对不常见的字用较长的编码，这样平均起来每个汉字的编码长度可以缩短。我们假定每一个汉字的频率是
p1, p2, p3, ..., p6700
它们编码的长度是
L1, L2, L3, ..., L6700
那么，平均编码长度是
p1×L1 + p2×L2 + ... + p6700×L6700

香农第一定理指出：这个编码的长度的最小值是汉字的信息熵，也就是说任何输入方面不可能突破信息熵给定的极限。当然，香农第一定理是针对所有编码的，不但是汉字输入编码的。这里需要指出的是，如果我们将输入法的字库从二级国标扩展到更大的字库 GBK，由于后面不常见的字频率较短，平均编码长度比针对国标的大不了多少。让我们回忆一下汉字的信息熵，
H = -p1 * log p1 - ... - p6700 log p6700。
我们如果对每一个字进行统计，而且不考虑上下文相关性，大致可以估算出它的值在十比特以内，当然这取决于用什么语料库来做估计。如果我们假定输入法只能用 26 个字母输入，那么每个字母可以代表 log26=
4.7 比特的信息，也就是说，输入一个汉字平均需要敲 10/4.7= 2.1 次键。

聪明的读者也许一经发现，如果我们把汉字组成词，再以词为单位统计信息熵，那么，每个汉字的平均信息熵将会减少。这样，平均输入一个字可以少敲零点几次键盘。不考虑词的上下文相关性，以词为单位统计，汉字的信息熵大约是8比特作用，也就是说，以词为单位输入一个汉字平均只需要敲 8/4.7=1.7 次键。这就是现在所有输入法都是基于词输入的内在原因。当然，如果我们再考虑上下文的相关性，对汉语建立一个基于词的统计语言模型，我们可以将每个汉字的信息熵降到 6 比特作用，这时，输入一个汉字只要敲 6/4.7=1.3 次键。如果一种输入方法能做到这一点，那么汉字的输入已经比英文快的多了。

但是，事实上没有一种输入方法接近这个效率。这里面主要有两个原因。首先，要接近信息论给的这个极限，就要对汉字的词组根据其词频进行特殊编码。事实上像王码这类的输入方法就是这么做到，只不过它们第一没有对词组统一编码，第二没有有效的语言模型。这种编码方法理论上讲有效，实际上不实用。原因有两个，第一，很难学；第二，从认知科学的角度上讲，人一心无二用，人们在没有稿子边想边写的情况下不太可能在回忆每个词复杂的编码的同时又不中断思维。我们过去在研究语言识别时做过很多用户测试，发现使用各种复杂编码输入法的人在脱稿打字时的速度只有他在看稿打字时的一半到四分之一。因此，虽然每个字平均敲键次数少，但是打键盘的速度也慢了很多，总的并不快。这也就是为什么基于拼音的简单输入法占统治地位的原因。事实上，汉语全拼的平均长度为 2.98，只要基于拼音的输入法能利用上下文彻底解决一音多字的问题，平均每个汉字输入的敲键次数应该在三次左右，每分钟输入 100 个字完全有可能达到。

另外一个不容易达到信息论极限的输入速度的原因在于，这个理论值是根据一个很多的语言模型计算出来的。在产品中，我们不可能占有用户太多的内存空间，因此各种输入方法提供给用户的是一个压缩的很厉害的语音模型，而有的输入方法为了减小内存占用，根本没有语言模型。拼音输入法的好坏关键在准确而有效的语言模型。

另一方面，由于现有输入方法离信息论给的极限还有很大的差距，汉语输入方法可提升的空间很大，会有越来越好用的输入方法不断涌现。当然，输入速度只是输入法的一项而不是唯一的衡量标准。我们也会努力把谷歌的输入法做的越来越好。大家不妨先试试现在的版本，http://tools.google.com/pinyin/，半年后再看看我们有没有提高。

数学之美 二十四 从全球导航到输入法——谈谈动态规划

今年九月二十三日，Google、T-Mobile 和 HTC 宣布了第一款基于开源操作系统 Android 的 3G 手机，其中一个重要的功能是利用全球卫星定位系统实现全球导航。这个功能在其它手机中早已使用，并且早在五六年前就已经有实现这一功能的车载设备出售。其中的关键技术只有两个：第一是利用卫星定位；第二根据用户输入的起终点，在地图上规划最短路线或者最快路线。后者的关键算法是计算机科学图论中的动态规划（Dynamic Programming）的算法。
    


在图论（请见拙著《图论和网络爬虫》）中，一个抽象的图包括一些节点和连接他们的弧。比如说中国公路网就是一个很好的“图”的例子：每个城市一是个节点，每一条公路是一个弧。图的弧可以有权重，权重对应于地图上的距离或者是行车时间、过路费金额等等。图论中很常见的一个问题是要找一个图中给定两个点之间的最短路径（shortest path）。比如，我们想找到从北京到广州的最短行车路线或者最快行车路线。当然，最直接的笨办法是把所有可能的路线看一遍，然后找到最优的。这种办法只有在节点数是个位数的图中还行得通，当图的节点数（城市数目）有几十个的时候，计算的复杂度就已经让人甚至计算机难以接受了，因为所有可能路径的个数随着节点数的增长而成呈指数增长（或者说几何级数），也就是说每增加一个城市，复杂度要大一倍。显然我们的导航系统中不会用这种笨办法。

所有的导航系统采用的都是动态规划的办法（Dynamic Programming），这里面的规划（programming）一词在数学上的含义是“优化”的意思，不是计算机里面编程的意思。它的原理其实很简单。以上面的问题为例，当我们要找从北京到广州的最短路线时，我们先不妨倒过来想这个问题：假如我们找到了所要的最短路线（称为路线一），如果它经过郑州，那么从北京到郑州的这条子路线（比如是北京-> 保定->石家庄->郑州，称为子路线一），必然也是所有从北京到郑州的路线中最短的。否则的话，我们可以假定还存在从北京到郑州更短的路线（比如北京->济南->徐州->郑州，称为子路线二），那么只要用这第二条子路线代替第一条，我们就可以找到一条从北京到广州的全程更短的路线（称为路线二），这就和我们讲的路线一是北京到广州最短的路线相矛盾。其矛盾的根源在于，我们假设的子路线二或者不存在，或者比子路线一还来得长。

在实际实现算法时，我们又正过来解决这个问题，也就是说，要想找到从北京到广州的最短路线，先要找到从北京到郑州的最短路线。当然，聪明的读者可能已经发现其中的一个“漏洞”，就是我们在还没有找到全程最短路线前，不能肯定它一定经过郑州。不过没有关系，只要我们在图上横切一刀，这一刀要保证将任何从北京到广州的路一截二，如下图。
    


那么从广州到北京的最短路径必须经过这一条线上的某个城市（图中蓝色的菱形）。我们可以先找到从北京出发到这条线上所有城市的最短路径，最后得到的全程最短路线一定包括这些局部最短路线中的一条，这样，我们就可以将一个“寻找全程最短路线”的问题，分解成一个个小的寻找局部最短路线的问题。只要我们将这条横切线从北京向广州推移，直到广州为止，我们的全程最短路线就找到了。这便是动态规划的原理。采用动态规划可以大大降低最短路径的计算复杂度。在我们上面的例子中，每加入一条横截线，线上平均有十个城市，从广州到北京最多经过十五个城市，那么采用动态规划的计算量是 10×10×15，而采用穷举路径的笨办法是 10 的 15 次方，前后差了万亿倍。

那么动态规划和我们的拼音输入法又有什么关系呢？其实我们可以将汉语输入看成一个通信问题，而输入法则是一个将拼音串到汉字串的转换器。每一个拼音可以对应多个汉字，一个拼音串就可以对应图论中的一张图，如下：
    


其中，Y1,Y2,Y3,……,YN 是使用者输入的拼音串，W11,W12,W13 是第一个音 Y1 的候选汉字，W21,W22,W23,W24 是对应于 Y2 的候选汉字，以此类推。从第一个字到最后一个字可以组成很多很多句子，我们的拼音输入法就是要根据上下文找到一个最优的句子。如果我们再将上下文的相关性量化，作为从前一个汉字到后一个汉字的距离，那么，寻找给定拼音条件下最合理句子的问题就变成了一个典型的“最短路径”问题，我们的算法就是动态规划。

上面这两个例子导航系统和拼音输入法看似没什么关系，但是其背后的数学模型却是完全一样的。数学的妙处在于它的每一个工具都具有相当的普遍性，在不同的应用中都可以发挥很大的作用。