matlab自适应滤波,基于MATLAB与DSP的自适应滤波器设计与实现
摘 要: 滤波是滤除信号中某些特定频率的波形的技术,在数字信号处理中,主要用于滤除噪声和干扰信号。由于噪声和干扰信号的不确定性,采用固定滤波系数的数字滤波器无法达到最佳的效果。自适应滤波器能够随着环境的改变而改动滤波器自身的参数和结构,从而能够随着噪声和干扰信号的不断变化修正滤波器的参数和结构,最终实现较理想的滤波。本文研究了最小均方差(LMS)算法,并结合自适应滤波器的结构和原理,设计出FIR结构自适应滤波器。最后给出MATLAB仿真结果,并利用DSP验证自适应滤波器的性能。
关键词: 自适应滤波器;MATLAB;LMS算法;FIR滤波器;DSP
0 引言
滤波即滤除信号中的噪声和干扰信号,提取有用信号的技术。滤波技术广泛应用于信号处理和信号分析中。在信号的获取和传输过程中出现的噪声,以及信号处理过程中的干扰信号都需要通过滤波技术滤除,来保证信号的安全性和可靠性。例如,实现雷达跟踪功能需要获取大量的船舶方位数据,在获取数据的过程中,会产生大量的随机干扰和测量误差。因此,为了准确地获取船舶瞬时的位置、加速度和速度等,需要利用滤波,将误差和随机干扰滤除,滤波技术在雷达跟踪功能实现中起到非常重要的作用。滤波器是一种允许特定频率信号通过的选频装置,通过这种装置获取有用的信号,滤除杂波。从最初的维纳滤波到后来的卡尔曼滤波,滤波器的实现有了很大的发展,随着技术的进步和社会的发展,需要处理的信号越来越复杂,要求实现的精度越来越高,同时对滤波器的要求也越来越高,其应用范围进一步得到拓展。随着滤波器的应用环境不断复杂化,对非线性的滤波技术研究得到进一步的发展。因此,自适应滤波器重新得到国内外研究者关注。自适应滤波器具有自我修正和跟踪的特点,主要适用于随机性噪声和干扰滤除。本文在自适应滤波器的原理和算法的基础上,利用MATLAB和DSP软件仿真环境设计实现自适应滤波的最优滤波。
1 自适应滤波器原理与结构
1.1 自适应滤波原理
自适应滤波即滤波器的参数可以自我调节,可以利用前一时刻的结果作为当前时刻滤波器的参数改变的依据,由此可以适应具有随机噪声和随时间变化的干扰信号的应用环境。就像生物能以各种有效的方式适应生存环境一样。自适应滤波器是一种具有反馈作用的闭环设置,它是一种特殊形式的维纳滤波器,可以通过反馈信息调节自身参数达到最优滤波。自适应滤波器没有复杂计算,实时性强,不需要已知输入信号,也可以对信号进行有效滤波。因此对于无法预知的信号固定滤波系数的传统滤波器无法滤除的杂波和噪声,自适应滤波器可以简单快速地输出理想期望信号。利用数字滤波器对噪声和干扰的最佳估计将输入信号中混有的干扰滤除,将目标信号与噪声和干扰信号有效地分离。随着自适应滤波技术的发展,其在电信、雷达、声呐、实时控制以及图像处理等领域都有广泛应用。
1.2 自适应滤波器的结构
自适应滤波器主要由数字滤波器和自适应算法两部分构成[1],其中,数字滤波器的系数可以调节,而自适应算法的作用就是调节和修正自适应滤波器的系数。如图1所示。图中自适应滤波器有x(n)和z(n)两个输入端,其中z(n)是包含目标信号s(n)和噪声d(n)的输入信号,s(n)和d(n)是不相关的两个信号,x(n)是与噪声d(n)有某种联系的z(n)的一种度量信号。y(n)可以通过数字信号滤波器得到,然后可以通过公式e(n)=z(n)-y(n)=s(n)+d(n)-y(n)得到误差信号e(n)。通过e(n)得到s(n)的最佳估计信号,而自适应滤波器的基本原理就是利用系数可调的数字滤波器将杂波和噪声从信号中滤除。
由图1自适应滤波器结构可知,基于滤波系数可调的要求,对于数字滤波器的选择包括有限长冲激响应滤波器(FIR)和无限长冲激响应滤波器(IIR)两种数字滤波器可选择。FIR型滤波器优势明显,它的系统更稳定,可以利用它实现多通带滤波器,同时它更容易实现线性相位[2]。IIR滤波器可以用更低的阶数实现与FIR相同的阻带衰减效果,但鉴于FIR易实现严格的线性相位、稳定性和任意的幅频特性等优点,另外FIR还有便于用DSP实现的优势,可以用节省存储空间的立即数乘加完成编程,因此本文的设计中自适应数字滤波器部分采用FIR滤波器横向结构。图2所示为FIR横向滤波器结构图。
2 自适应滤波算法
2.1 LMS自适应滤波算法
Widrow和Hoff提出的最小均方差(LMS)算法在实践中被广泛应用,其具有计算量小和易于实现的特点[3]。自适应算法通常由三大重要的技术指标来衡量其优劣:时变系统随参数变化导致系统特性变化的检测能力、输出信号收敛到期望信号的速度以及对系统稳定性的调节能力。自适应滤波器实现功能的关键是寻找出均方误差最小时滤波器权系数Wi的值,整个过程中利用ε和各x(n)的值,再根据上述的条件,通过算法找出Wi的值,实现自动调节Wi值的滤波器。所有的滤波器系数调整算法都是设法使输出y(n)和目标信号d(n)之差 e(n)的均方值最小化,并且根据这个判据来修改权系数。均方误差ε表示为:
其中:R=E[X(n)XT(n)]为N×N的自相关矩阵,它是输入信号采样值间的相关性矩阵。P=E[d(n)X(n)]为N×1互相关矢量,代表理想信号d(n)与输入矢量的相关性。
由式(4)可知,自适应滤波器的权系数与滤波器的抽头系数相关联,可以根据已知的矩阵R和矢量P以及抽头系数的二次函数方程式求得W的解。根据二次函数曲线具有唯一最小函数值的性质,可以得出滤波器输出误差函数具有最小值即滤波得到最优效果,在数学上可以利用梯度法求得此最小值,为了简单起见,设W是一维的,则E[e2(n)]与W的关系成为一个抛物线。如图3中在W*点获得最小均方误差。根据递推关系式,利用梯度矢量法计算出抛物曲面的最低点。而自适应的过程就是在梯度矢量的负方向上逐渐校正滤波器系数,调节加权系数W使均方误差最小,相当于沿超抛物形曲面下降到最小值,获得最佳滤波或准最优工作状态。
实际上,自适应滤波与维纳滤波最主要的差别就是自适应滤波增加了一个可以识别控制滤波器系数的部分,可以根据期望输出信号与滤波器实际输出信号的比较,用误差函数值去控制和调整滤波器系数直至误差达到最小值。也正因如此,找到一个能求得加权系数,直至W=W*,E[e2(n)]=min的递推式是LMS算法的核心。
2.2 RLS自适应滤波算法
另外一种区别于LMS算法的具有较快收敛速度的自适应算法即RLS,但是它存在实时性差的缺点,限制了其应用。RLS自适应滤波器的最佳滤波权系数需要用输入信号自相关矩阵的逆来求得[4]。针对RLS算法计算复杂、实时性差但收敛于期望信号的速度比较快的特性,只要加以改进就能使其得到很好的应用,因此人们提出了改进的RLS算法,即变换域自适应滤波算法。
2.3 变换域自适应滤波算法
对于某些强相关的信号或难以滤除的信号,利用变换域的思想可以将目标信号轻松地分离出来,变换域可以轻松解决时域疑难问题,频域变换、小波变换都属于变换域。1979年Dentino首次将变换域的思想应用在自适应滤波上,对变换域自适应滤波算法做了全面的总结和解释。变换域自适应滤波算法就通过正交变换把时域信号转变为频域或小波域等信号,用归一化的能量平方根来表示变换后的信号,然后结合自适应算法进行滤波。随着技术的不断发展,变换域自适应滤波算法不断得到推广。由于LMS算法是依赖于输入信号求其收敛性,所以针对强相关的信号,LMS自适应滤波的效果大大降低[5]。基于对以上三种自适应算法的研究,本文主要针对LMS自适应算法对其进行MATLAB与DSP设计与实现。
3 自适应滤波器的仿真实现
3.1 FIR滤波算法MATLAB仿真实现
MATLAB能方便地以书写计算公式的思维方式对所要实现的功能编程,具有强大的语言功能,在数字信号处理方面具有很大的优势。另外,MATLAB具有很多封装完整的可供用户使用的开源数据和工具箱,如系统辨识工具箱、神经网络工具箱、信号处理工具箱、模糊推理系统工具箱等。图形、数学、编程还可以通过Simulink模块来实现,可将自己建好的模型打包成块,以后便可以直接调用,非常方便。它还提供了与Windows编程相结合的矩阵运算、图形绘制、数据处理和图形处理等工具,在自动控制、图像信号处理、雷达工程、信号分析、优化设计等领域得到了广泛应用[6]。
自适应LMS算法可以用MATLAB方便地实现。自适应LMS算法的原理是利用最陡下降法以及时间n=0的滤波系数矢量和任意的起始值W(0)通过迭代公式更新滤波器权系数W(n),其具体方法如下:
(1)求得误差信号e(n):e(n)=d(n)-x(n),其中 d(n)为滤波器期望输出信号,x(n)为滤波器输入信号。
(2)求滤波器系数。利用如下递推公式更新矢量值:
w(n)=w(n-1)+2*e(n)*x(n)
其中
![]() 为收敛因子。
为收敛因子。
(3)从时间参数n=0开始递增加1,求误差信号,重复上述计算直到求得最小均方误差实现最优滤波为止。
LMS的核心算法如下:
function[yn,W,en]=LMS(xn,dn,M,mu,itr)
en=zeros(itr,1);
W=zeros(M,itr);
for k=M:itr
x=xn(k:-1:k-M+1);
y=W(:,k-1).′*x;
en(k)=dn(k)-y;
W(:,k)=W(:,k-1)+2*mu*en(k)*xn(k);
end
yn=inf*ones(size(xn));
for k=M:length(xn)
x=xn(k:-1:k-M+1);
yn(k)=W(:,end).′*x;
end
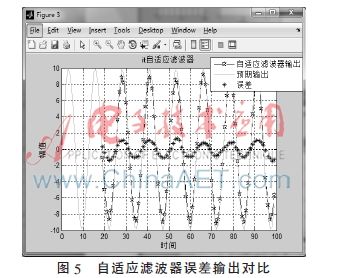
通过实验产生输入信号x(n),期望信号为d(n),两者相减得到误差信号e(n),然后通过调用LMS算法从宽甸信号中提取单频信号,实验结果如图4、图5所示,进一步调整收敛因子,观察结果变化发现,收敛因子越大,滤波器的抽头数越多,期望信号能以更快的速度收敛到输出信号,同时也存在稳态误差越大的风险,所以应选用合适的收敛因子和滤波器阶数,在收敛速度和误差稳态范围上得到权衡。
3.2 自适应滤波器DSP设计实现
通过MATLAB的仿真实验,LMS自适应滤波器的滤波特性得到验证,接下来用TMS320C6713设计实现LMS自适应滤波器。本文设计实现的是应用LMS算法的FIR型自适应滤波器[7]。其自适应滤波器的程序流程图如图6所示。
由图6自适应滤波器设计流程图可知,其设计过程主要包括三个步骤:
第一步:程序初始化
为输入信号x(n)、滤波输出信号y(n)、误差信号 e(n)分配存储区,同时为输入信号的长度(num)、滤波器阶数(coeff)设置初值,本文设置为num=1 024,coeff=16。收敛因子fU=0.000 5。
第二步:调用信号输入子程序产生输入信号x(n),输出信号y(n),误差信号e(n)。
其程序如下:
for(i=0;i
{
x[i]=256*sin(i*2*PI/34);//初始化输入信号
y[i]=z[i]=0;//初始化输出信号误差信号
}
第三步:调用LMS算法
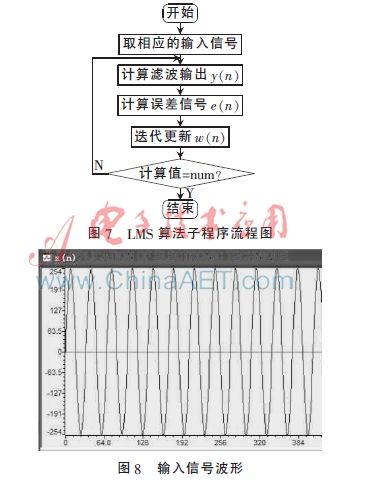
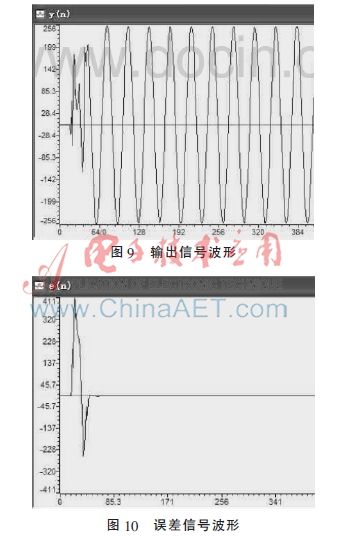
主程序运行时不断调用LMS算法子程序,来计算滤波信号输出,检测信号是否完成滤波,如未完成重复第三步工作[8]。其LMS算法子程序流程图如图7。LMS算法子程序为int FIRLMS(int*nx,float*nh,int nError,int nCoeffNum)。在CCS环境下用C语言编写程序,通过编译、链接后生成公共目标代码,选择View/Graph/Time/Frequency,进入Graph Prorerty Dialog对话框,设置合适的图形显示参数,在显示窗口显示自适应滤波器DSP仿真结果,如图8、图9、图10所示。
LMS核心算法子程序如下:
int FIRLMS(int*nx,float*nh,int nError,int nCoeffNum)
{
int i,r;
float fWork;
r=0;
for(i=0;i
{
fWork=nx[i]*nError*fU;
//h(n+1)=h(n)+2u*e(n)*x(n)
nh[i]+=fWork;
r+=(nx[i-i]*nh[i]);
}
r/=128;
return r;}
通过观察输出波形与输入波形,可以看出输出波形一开始与输入波形相差较大,但通过自适应滤波器不断调节加权系数w(n),使输出波形逐渐符合输出要求。由此也可验证此自适应滤波器LMS算法的有效性,其能够很好地滤除数字信号中的噪声,较好地还原了数字信号的信息,在数字信号处理领域有很好的应用价值。
4 结束语
本文对自适应滤波器的原理和结构图进行了分析,利用先进的MATLAB仿真技术进行仿真最后进行DSP的设计实现。仿真结果充分表明,自适应滤波器可以根据噪声信号的频率进行跟踪并以此来很好地滤除信号中的噪声。并且,在噪声和信号特性不断随时间变化的同时,自适应滤波器可以利用自适应算法不断调整和修正冲激响应函数系数,能很好地适应输入环境的变化。这充分突出了自适应滤波器的优势,使其具有更广泛的应用领域和广阔的发展前景,例如通信信道的自适应均衡、心电图的电源干扰消除、系统模型识别和雷达波束形成等领域。基于不同的自适应算法以及不同的数字滤波器结构可构成不同结构的自适应滤波器,本文重点研究了基于LMS算法的FIR型自适应滤波器。本文还有待于进一步研究和改进,以提高自适应滤波器的精度和收敛速度。
参考文献
[1] 贡镇.基于DSP的自适应滤波器的设计与实现[J].现代电子技术,2013(17):62-64.
[2] 李茂清,王洁,陈强,等.基于MATLAB程序的FIR滤波器设计实现[J].电力学报,2008(2):87-90.
[3] 张玲玲,唐晓英,刘伟峰.一种新的变步长LMS自适应滤波算法性能分析[J].生命科学仪器,2005(5):39-41.
[4] 郭华.自适应滤波算法及应用研究[D].西安:西北师范大学,2007.
[5] 蒋薇薇,杨萍,王昱洁.基于变步长LMS算法的自适应滤波器研究[J].仪器仪表学报,2010,31(8):478-480.
[6] 刘光普,高玉春.MATLAB在通信原理教学中的应用[J].数据采集与处理,2012(S1):39-42.
[7] 莫晶.基于自适应噪声抵消系统的不同滤波算法研究[D].昆明:云南师范大学,2014.
[8] 许国威,马胜前,危淑平.自适应滤波RLS算法研究与DSP实现[J].计算机技术与发展,2010(10):35-38.