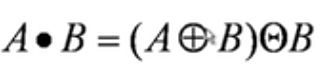数字图像处理--图像的形态处理学
形态学基本概念
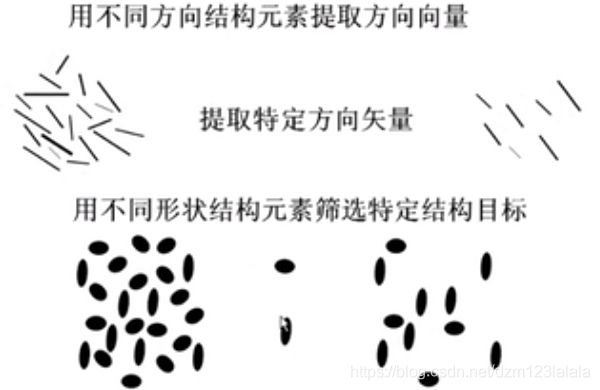
基本思想:用一定形态的结构元素去度量和提取图像中的对应形状，达到分析和识别的目的。
可用于图像处理的各个方面，包括图像分割，特征抽取，边界检测等等。
对图像处理的理论和技术产生了重大影响，已经构成一种新的图像处理方法和理论，成为一个重要的研究领域。
在图像处理中的应用主要是：
- 对图像进行观察和处理，从而达到改善图像质量的目的
- 米哦啊书和定义图像的各种几何参数和特征，如面积，周长，联通度，颗粒度，骨架和方向性等。
几个概念
补集：不包含 A A A的所有元素组成的集合
A C = { w ∣ w ∉ A } A^C=\{w|w \notin A\} AC={w∣w∈/A}
集合的差：
A − B = { w ∣ w ∈ A , w ∉ B } = A ∩ B C A-B=\{w|w\in A,w \notin B \}=A \cap B^C A−B={w∣w∈A,w∈/B}=A∩BC
反射： B ^ = { w ∣ w = − b , b ∈ B } \hat{B}=\{w|w=-b,b\in B\} B^={w∣w=−b,b∈B}关于原点取对称。如果集合 B B B本身关于原点对称，那么 B = B ^ B=\hat{B} B=B^
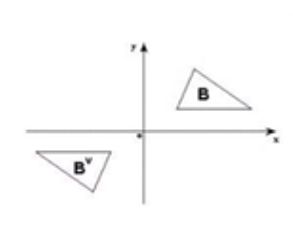
平移：
( A ) z = { c ∣ c = a + z , a ∈ A } (A)_z=\{c|c=a+z,a \in A\} (A)z={c∣c=a+z,a∈A}
腐蚀与膨胀
腐蚀和膨胀是形态学处理的基础，许多形态学算法都是以这两种运算为基础的。
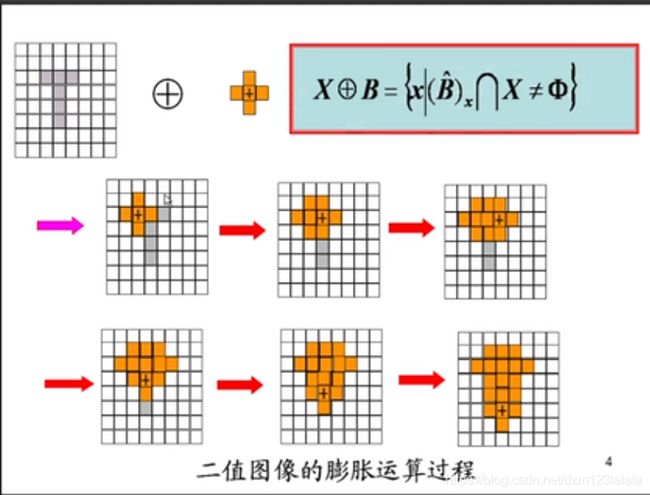
膨胀
集合 A A A被集合 B B B膨胀，定义为：
A ⊕ B = { z ∣ ( B ^ ) z ∩ A ≠ Φ } A\oplus B=\{z|(\hat{B})_z \cap A \neq \Phi\} A⊕B={z∣(B^)z∩A̸=Φ}
B称为结构元素。结构元素先进行反射，之后进行z平移，之后和A进行交运算，若击中，记录下平移量z。
若B对称，则把B平移a后得到 B a B_a Ba。若 B a B_a Ba击中A，记下a点，所有满足上述条件的a点组成的集合称为A对B的膨胀。
D B ( A ) = A ⊕ B = { a ∣ B a ↑ A } D_B(A)= A\oplus B=\{a|B_a\uparrow A\} DB(A)=A⊕B={a∣Ba↑A}
如果用 d 4 \frac{d}{4} 4d大小的结构元素取膨胀d大小的结构元素，会得到边缘加厚 d 8 \frac{d}{8} 8d的结果。
膨胀最简单的应用是 将裂缝桥接起来。
膨胀最简单的应用之二是填充目标中的空洞。
腐蚀
使用集合B对集合A进行腐蚀，定义为：
A ⊝ B = { z ∣ ( B ) z ⊆ A } A\circleddash B=\{z|(B)_z \subseteq A\} A⊝B={z∣(B)z⊆A}
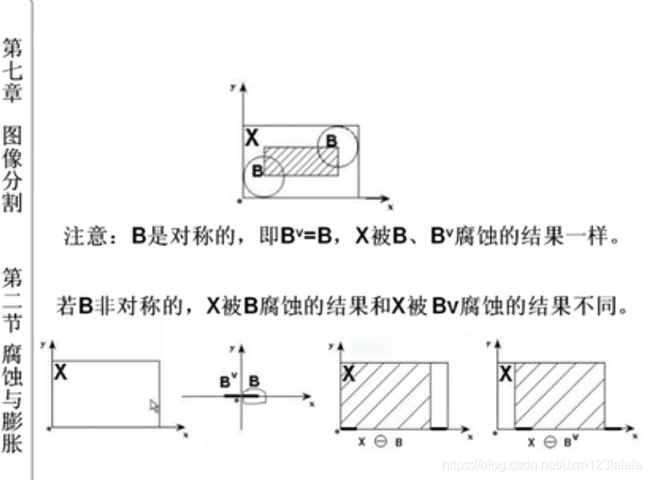
把结构元素B平移a后得到 B a B_a Ba，若 B a B_a Ba包含于X，则记下这个a点，所有满足上述条件的a点组成的集合称作X被B腐蚀的结果。
E B ( A ) = A ⊝ B = { a ∣ B a ⊂ A } E_B(A)=A\circleddash B=\{a|B_a \subset A\} EB(A)=A⊝B={a∣Ba⊂A}
膨胀和腐蚀的性质
-
膨胀和腐蚀运算的对偶性
( X ⊝ B ) C = X C ⊕ B ^ ( X ⊕ B ) C = X C ⊝ B ^ (X\circleddash B)^C=X^C \oplus \hat{B} \quad \quad (X\oplus B)^C=X^C \circleddash \hat{B} (X⊝B)C=XC⊕B^(X⊕B)C=XC⊝B^
X对B的腐蚀运算的补集等于X的补集对B的反射的膨胀运算；
X对B的反射运算的补集等于X的补集对B的腐蚀的膨胀运算。
河岸的补集为河面，对河岸的腐蚀等价于对河面进行膨胀。 -
膨胀运算具有互换性，腐蚀运算不具有互换性。
( X ⊕ B ) ⊕ A = ( X ⊕ A ) ⊕ B (X\oplus B)\oplus A=(X\oplus A)\oplus B (X⊕B)⊕A=(X⊕A)⊕B
( X ⊝ B ) ⊝ A ≠ ( X ⊝ A ) ⊝ B (X\circleddash B)\circleddash A \neq (X\circleddash A)\circleddash B (X⊝B)⊝A̸=(X⊝A)⊝B -
腐蚀和膨胀具有组合性。
开运算与闭运算
膨胀和腐蚀运算，对目标的后处理有着非常好的作用，缺点是，改变了原目标物的大小。
为了解决这一问题，考虑到腐蚀与膨胀时一对对偶运算，将膨胀和腐蚀运算同时进行，便构成了开运算和闭运算。
开运算
使用结构元素B对集合A进行开操作，定义为：
A ∘ B = ( A ⊝ B ) ⊕ B A \circ B=(A\circleddash B)\oplus B A∘B=(A⊝B)⊕B
开运算
- 消除细小对象
- 在细小粘连处分离对象
- 在不改变形状的前提下，平滑对象的边缘。
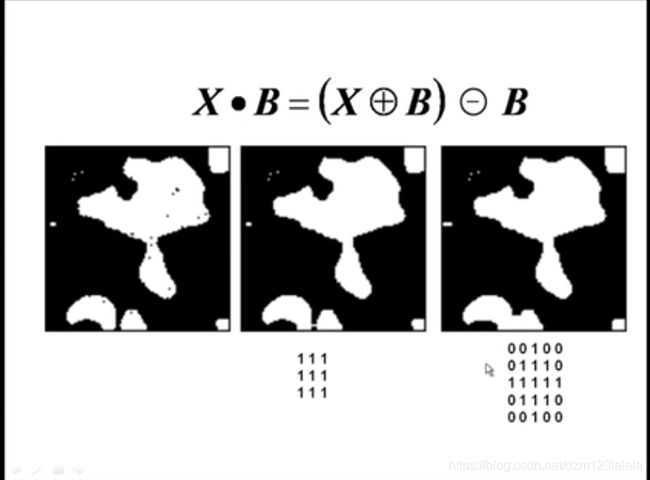
3 × 3 3\times 3 3×3和 5 × 5 5\times 5 5×5的矩形结构元素分别进行开运算：
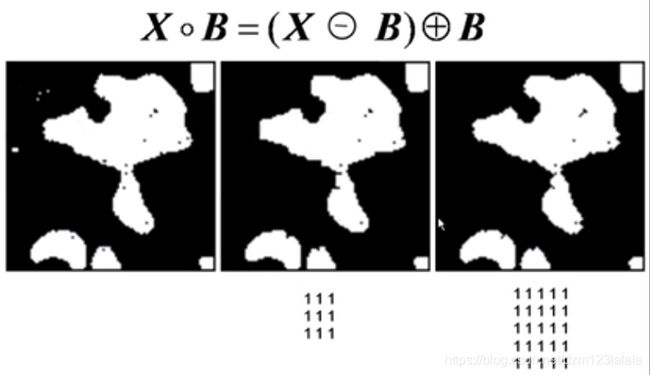
去除了细小孔洞，平滑了边缘。
如果B是非对称的，进行开运算时要用B的对称集 B ∨ B^\vee B∨膨胀，否则，进行开运算时结果会和原来比发生平移，当结构元素为非对称时，腐蚀的结果会发生平移，然后再进行膨胀时，会向另外一侧平移。
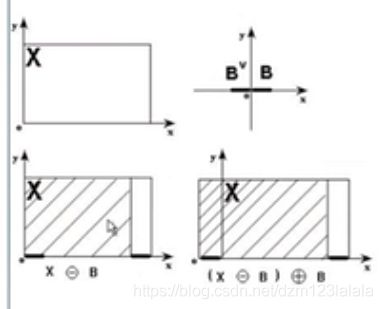
闭运算
使用结构元素B对集合A进行闭操作，定义为：
闭运算作用：
- 填充对象内细小空洞
- 链接接近的对象
- 再不明显改变面积的前提下，平滑对象的边缘
开运算和闭运算的性质
开运算和闭运算也是对偶运算
X开运算的补集等于X补集的闭运算，或者X闭运算的补集等于X补集的开运算。
如何理解：两个小岛之间有小桥，岛和桥看作是处理对象X，则X的补集为大海。对岛桥进行开处理等于对大海进行闭处理
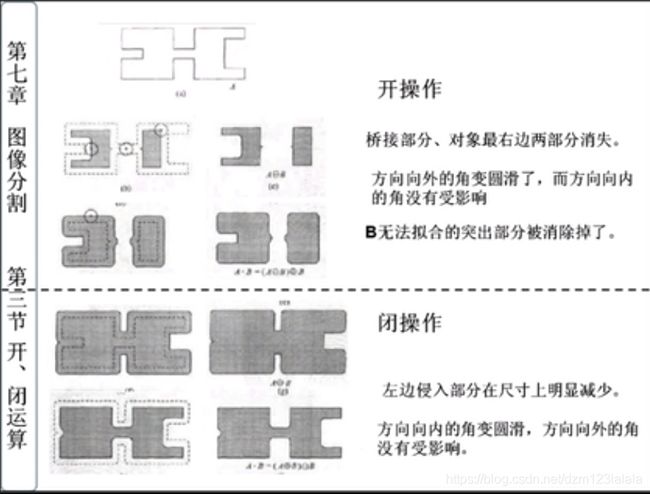
开操作一般是使得对象的轮廓变得平滑，断开狭窄的间断和消除细小的突出物。
闭操作同样是使得轮廓更为光滑，通常是消除狭窄的尖端和长细的鸿沟，消除小的空洞，填补轮廓线中的断裂。
二值数学形态学基本算法
形态滤波
用不同的方向结构元素提取方向向量
图像的边缘提取
图像的边缘线或者棱线时图像中信息量最为丰富的区域。提取边界或者边缘也是图像分割的重要组成部分。
先腐蚀图像，然后用原图像减去腐蚀后的图像，相减即得到边缘。
提取物体的轮廓边缘的形态学变换为：
Y = X − ( X ⊝ B ) Y=X-(X\circleddash B) Y=X−(X⊝B)
区域填充
区域时边界所包围的部分，边界是区域的轮廓线，区域和边界可以互求。
填充过程实际上就是从边界上某一点p开始做以下迭代运算，用结构元素对其进行膨胀，求补和求交集的过程。
X k = ( X k − 1 ⊕ B ) ∩ A c X_k=(X_{k-1} \oplus B)\cap A^c Xk=(Xk−1⊕B)∩Ac
B是结构元素， X 0 X_0 X0是边界种子点，A是边界图像。
在进行形态学填充之前必须了解一点：当我们的边界是4连通边界时，我们使用的结构元素为8连通；当我们的连通边界为8连通时，我们需要用4连通的结构元素。
具体为什么可以这样做，拿那个结构元素在边缘上试一下就知道了。
击中击不中变换
